基于ADC方法的炮射导弹系统效能评估

李春臻，刘婵媛，高文霞，班 伟，杨 煜

(1.中北大学 机电工程学院，山西 太原 030051； 2.新乡航空工业(集团)有限公司，河南 新乡 453000；3.中国船舶重工集团第七一〇研究所，湖北 宜昌 443003)

0 引言

武器系统效能是指在所拟定预定条件下使用某种武器系统，该武器系统在规定时间内完成规定任务的程度[1]。它是通过综合描述系统效能中不同属性的多个指标得到的。而且武器系统效能是一种预测的结果、输出、后果或操作，即正确地做正确的事情，以达到最终的目的。在武器系统效能评估过程中还需考虑可靠性、维修性、安全性与各种偶然人为因素。由此看出武器系统效能评估具有概率性、相对性、时限性和局限性的特点，所以采用定性方法对武器系统进行分析、综合、评估和比较是研究武器系统效能与综合质量特性是很有必要的[2]。而且对武器系统效能进行评估有利于真实反映武器系统作战能力，对武器系统的发展具有很重要的现实意义[3]。

炮射导弹作为一种新型的攻击手段，是利用坦克或者其他火炮平台发射的一种制导炮弹，相对于其他常规导弹，炮射导弹具有射程远、命中精度高、杀伤威力大等优点，从而极大的增强了坦克装甲车辆的综合作战能力[4]。考虑炮射导弹系统为许多分系统组成的整套系统，各个分系统之间既有串联关系，又有并联关系。也就是说，炮射导弹分系统无法完成拟定作战任务，使得整个炮射导弹系统无法进行正常工作；而有的炮射导弹分系统出现错误，整体炮射导弹系统依然可以完成拟定任务。本文选择应用最为广泛的ADC法为基础，根据研究的需要对其各方面做了适应性修改，形成一种适用于炮射导弹的ADC法，并开发了系统效能评估软件工具。ADC(availability dependability capacity)方法是美国工业界武器系统效能咨询委员会(WSEIAC,weapon system effectiveness industry advisory committee)在系统效能定义的基础上建立的，其目的在于根据可用性(availability)、可信性(dependability)和能力(capacity)三大要素评价装备系统，把这三大要素组合成一个表示装备系统总性能的单一效能量度[5]。定义为预算一个系统完成一组特定的任务程度的量度，是可用性向量A、可信性向量D和能力向量C的乘积，且规定ADC方法并非是一个可以直接应用得数学公式，它作为一个基本程序需要去建立相应的数学模型，一般情况是通过马尔可夫假定来确定武器系统状态转移，特定情况需要确定表征值来表示武器系统状态转移[6]。

1965年，美国工业界武器系统效能咨询委员会(WSEIAC)提出了一种方法ADC效能评估法[7]，从综合评估可用度、可靠度和能力等方面考量武器装备对作战效能的具体影响，从而能较为全面的反映出多项战术技术指标及武器装备作战性能对装备整体影响的综合表现。ADC方法到现在已经发展了半个多世纪，其在武器装备效能评估方面的理论研究和实际应用日益完善，现在梳理ADC效能评估法的国内外研究现状，为日后的工作和改进方向能提供指导。

黄贡献等[8]基于ADC模型，针对自行火炮营系统的功能特点和组成，通过可用度向量、可信赖矩阵和能力向量三者的函数建立基本数学计算模型，对自行火炮营系统的作战效能进行了评价。孟锦等[9]基于ADC模型，对侦查卫星系统自身特点进行了分析，并针对系统效能评估不能反映侦察卫星在侦查过程中的动态变化问题建立了动态ADC模型。宋朝和[10]基于ADC模型，根据雷达的侦查定位和数据处理的传输能力，运用有关的聚合法计算雷达的侦查能力，从而实现侦查雷达的效能分析。徐皓等[11]基于ADC模型建立了鱼雷作战的效能评估模型。徐晓明等[12]基于ADC模型建立无人布雷系统布雷阶段效能评估指标体系，突出运行条件和环境适应等因素的影响，从而建立无人布雷系统布雷阶段效能评估模型。程晓明等[13]基于ADC模型，从目标显现到雷达散射和目标杀伤建立了多无人机协同编队效能模型，参考无人机编队协同突防的例子，建立了地空导弹防御系统雷达探测的数学模型。G.Jiao等[14]基于ADC模型，提出了有关舰载导航设备综合效能的理论。李彤岩[15]等基于ADC模型，针对通信网络性能指标多和效能评估困难的问题，根据可视化的方法，提出了基于ADC模型的效能评估方法。王君等[16]基于ADC模型，分析了武器系统的可靠性逻辑结构，建立了一种低空近程低空带单武器系统效能评估的数学模型。陈强等[17]基于ADC模型，结合指标体系的选取和确立原则，从数据链系统的信息支持能力出发，建立了数据链系统作战效能指标体系。郑锦等[18]基于ADC模型，建立了有关影响水面舰艇作战系统效能评估因素的数学模型，并根据典型水面舰艇的对空作战任务效能的库组，验证了所提模型的有效性。

1 炮射导弹系统效能评估概念模型

炮射导弹是一种新型运用在坦克等装甲车辆的精准打击武器，它是由制导部、推进系统、战斗部、电子设备和弹体结构组成，炮射导弹结构示意如图1所示。

炮射导弹系统效能评估概念模型包括3个分支：可用性、可信性和固有能力。可用性由可靠性和维修性所确定；可信性由发射可靠度、飞行可靠度和作用可靠度所确定；能力包括弹体结构系统、制导系统、推进系统和战斗系统4个部分，各分系统按组合逐层展开为基本功能单元。能力是各分系统按规定联合运行而产生的附加能力，对可用性、可信性无影响。炮射导弹系统效能评估体系如图2所示。

图2 炮射导弹系统效能组成部分

2 炮射导弹系统效能评估数学模型

2.1 系统效能数学模型

ADC方法中，系统效能E是预计系统满足一组特定任务要求之程度的量度，是有效性、可依赖性和能力的函数。可用性A是在开始执行任务时系统状态的量度，是装备、人员、程序三者之间的函数。可信性D是在已知开始执行任务时系统状态的情况下，在执行任务过程中的某一个或某几个时刻系统状态的量度。固有能力C是在已知执行任务期间的系统状态的情况下，系统完成任务能力的量度。其中系统效能E可以表示为：

E=ADC=AD1C+AD2C+…ADiC=

式中，A表示系统可用性向量，an是系统在初始贮存阶段处于状态n时的概率；D表示系统可信性矩阵，Di表示系统各个分系统的可信性矩阵，dnn是系统在工作阶段状态由n变为n的概率；C表示系统固有能力向量，cn是系统处于状态n中完成所规定任务的能力。

2.2 系统可用性向量数学模型

设系统状态变量为S，则由4个分系统的不同状态组合的到的系统状态向量为：

S=[s1,s2,s3,…,s16]

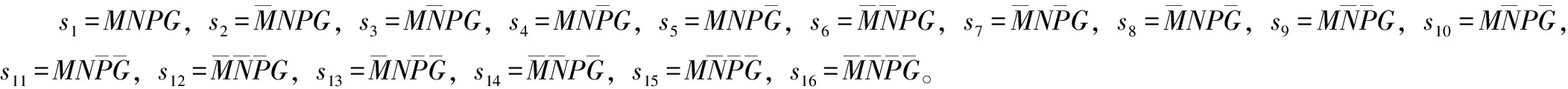
设CM、CN、CP、CG分别为4个系统分别处于正常状态的概率(可用度)，则有：

设ai为系统处于状态si(i=1,2,…,16)的概率，并设定4个系统在概率上相互独立，则有：

a1=B(s1)=B(MNPG)=

B(M)B(N)B(P)B(G)=CMCNCPCG

依次类推：

a2=(1-CM)CNCPCG;a3=CM(1-CN)CPCG;

a4=CMCN(1-CP)CG;a5=CMCNCP(1-CG);

a6=(1-CM)(1-CN)CPCG;

a7=(1-CM)CN(1-CP)CG;

a8=(1-CM)CNCP(1-CG);

a9=CM(1-CN)(1-CP)CG;

a10=CM(1-CN)CP(1-CG);

a11=CMCN(1-CP)(1-CG);

a12=(1-CM)(1-CN)(1-CP)CG;

a13=(1-CM)CN(1-CP)(1-CG);

a14=(1-CM)(1-CN)CP(1-CG);

a15=CM(1-CN)(1-CP)(1-CG);

a16=(1-CM)(1-CN)(1-CP)(1-CG)

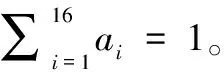
由此可以得到系统的可用性向量：

A=(a1,a2,a3,…,a16)

2.3 系统可信性矩阵数学建模

由建立的炮射导弹系统效能模型可知[19]，系统可信性由发射可靠度、飞行可靠度和作用可靠度所构成，因此系统可信性矩阵分为三个分模块矩阵构成。

由建立的系统可用性向量模型可知，系统共有16种状态，因此系统可信性矩阵为16阶方阵。

设4个分系统的发射可靠度分别为RM、RN、RP、RG，发射时间为t，并设定F留为导弹留膛概率，F膛为导弹膛炸概率，则有：

R=1-F留-F膛

假如设定各个系统在执行发射任务时发生故障不予修复，则各个系统状态转移的概率为：

B(M→M)=RM,B(N→N)=RN,

B(P→P)=RP,B(G→G)=RG;

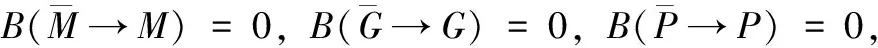
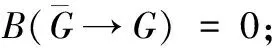
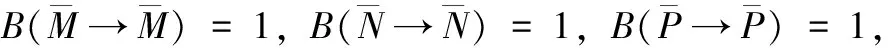
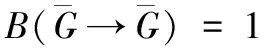
设系统由状态ci到状态cj的概率为dij(i、j=1,2，…，16),设定3个系统分别在概率上相互独立，所以得到：

d11=B(s1→s1)=B(MNPG→MNPG)=

B(M→M)B(N→N)B(P→P)B(G→G)=RMRNRPRG;

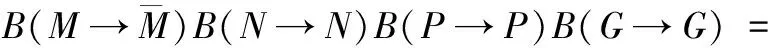
(1-RM)RNRPRG

其余依次类推。

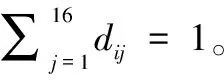
由此可以得到系统的发射可靠度可信性矩阵为：

设4个分系统的飞行可靠度分别为IM、IN、IP、IG,飞行时间为t,并设定F失控为炮射导弹弹体失控概率，F信息场为导弹信息场发生故障概率，F未进入为导弹未进入信息场概率，F弹体为导弹弹体信号强度低概率，F发动机为导弹发动机发生故障概率，则有：

I=1-F失控

F失控=F信息厂+F未进入+F弹体+F发动机

按照上述发射可靠度可信性矩阵类推，由此得到系统的发射可靠度可信性矩阵为：

设4个分系统的作用可靠度分别为LM、LN、LP、LG，作用时间为t，并设定F瞎火为炮射导弹瞎火概率，F引信为炮射导弹引信瞎火概率，F延时器为炮射导弹延时器发生故障概率，F线路为炮射导弹触发线路断路导致故障概率，则有：

L-1-F瞎火

F瞎火=F引信+F延时器+F线路

按照上述发射可靠度可信性矩阵类推，由此得到系统的作用可靠度可信性矩阵为：

2.4 系统固有能力矩阵数学建模

系统固有能力由弹体结构系统、制导系统、推进系统和战斗系统4个部分组成。各部分主要控制炮射导弹的导弹质心参数、导弹射程参数、导弹制导控制力矩参数和导弹破甲深度参数。根据能力的概念模型，能力矩阵如下：

C=(c1,c2,c3...,c16)T

Cj=Xμ1Sμ2Mμ3Pμ4

式中,Cj为炮射导弹系统处于状态j时所具有的能力参数；M为炮射导弹质心参数；N为炮射导弹射程参数；P为炮射导弹制导控制力矩参数；G为炮射导弹破甲深度参数。μ1,μ2,μ3,μ4为各固有能力权重参数。

2.4.1 炮射导弹质心参数

炮射导弹质心参数是指炮射导弹各系统部件的质心位置，是导弹总体设计单元的重要参数[20]。合理调整导弹质心位置有利于提高导弹的结构性能，能够提高炮射导弹飞向目标的准确性，炮射导弹质心参数X的数学模型为：

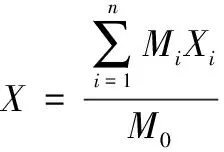
式中,Mi为炮射导弹的各部件质量，Xi为炮射导弹的各部件直径，M0为炮射导弹各部件总质量。

2.4.2 炮射导弹射程参数

炮射导弹射程参数是指炮射导弹弹体发射位置与最终导弹落点之间的距离[21]，确定炮射导弹的射程参数有利用提高炮射导弹的命中率且能够提高炮射导弹性能。炮射导弹射程参数S的数学模型为：

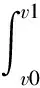
式中,v为炮弹导弹的各阶段速度值，f(t)为炮射导弹各阶段的时间与速度的曲线函数。

2.4.3 炮射导弹制导控制力矩参数

对炮射导弹的设定任务是准确命中并有效地毁伤预定目标，设定炮射导弹制导控制力矩参数使得控制力矩能够有效抵消外部干扰力矩，从而使得炮射导弹具有良好的抗干扰能力[22]。炮射导弹制导控制力矩参数M的数字模型为：

M=CMPSAL

式中,L为炮射导弹制导系统中舵机的力臂长度，CM为舵机排气系数，一般取0.6～0.9，PS为舵机活塞进气压力，A为舵机活塞面积。

2.4.4 炮射导弹破甲深度参数

炮射导弹破甲深度是衡量炮射导弹战斗部威力的一个重要因素，能够体现炮射导弹对目标的毁伤能力，使得炮射导弹能够精确毁伤并完后才能预定任务[23]。炮射导弹破甲深度参数P的数学模型为：

HY=k1·k2·k3·dk

式中,β1为炮射导弹所穿材料的经验系数，本文取值0.7；dk为炮射导弹战斗部药型罩内径；α为炮射导弹战斗部药型罩半锥角；HY为炮射导弹有利精炸高，k1为炸高与药型罩口径之比，本文取值3.8；k2为与炮射导弹临界速度有关的系数，本文取值1.1；k3为炮射导弹战斗部炸药爆炸速度的系数，规定为1～1.3，本文取值1。

2.4.5 固有能力各参数归一化处理

导弹固有能力需要对炮弹导弹质心参数、炮射导弹射程参数、炮射导弹制导控制力矩参数和炮射导弹破甲深度参数进行归一化处理，本文采用隶属度函数进行参数归一化。隶属度函数是应用于模糊参数或概念集中处理的一个概念，表示某个样本隶属于某个集合的函数[24]。炮射导弹质心参数、射程参数、制导控制力矩参数和破甲深度参数隶属度函数如下：

质心参数隶属度函数：

射程参数隶属度函数：

制导控制力矩参数隶属度函数：

破甲深度参数隶属度函数：

3 炮射导弹系统效能评估步骤

以设计改进后的典型的APS05型125毫米激光架束炮射导弹为例进行半实物样机试验，炮射导弹性能如表1所示，计算炮射导弹的系统效能。

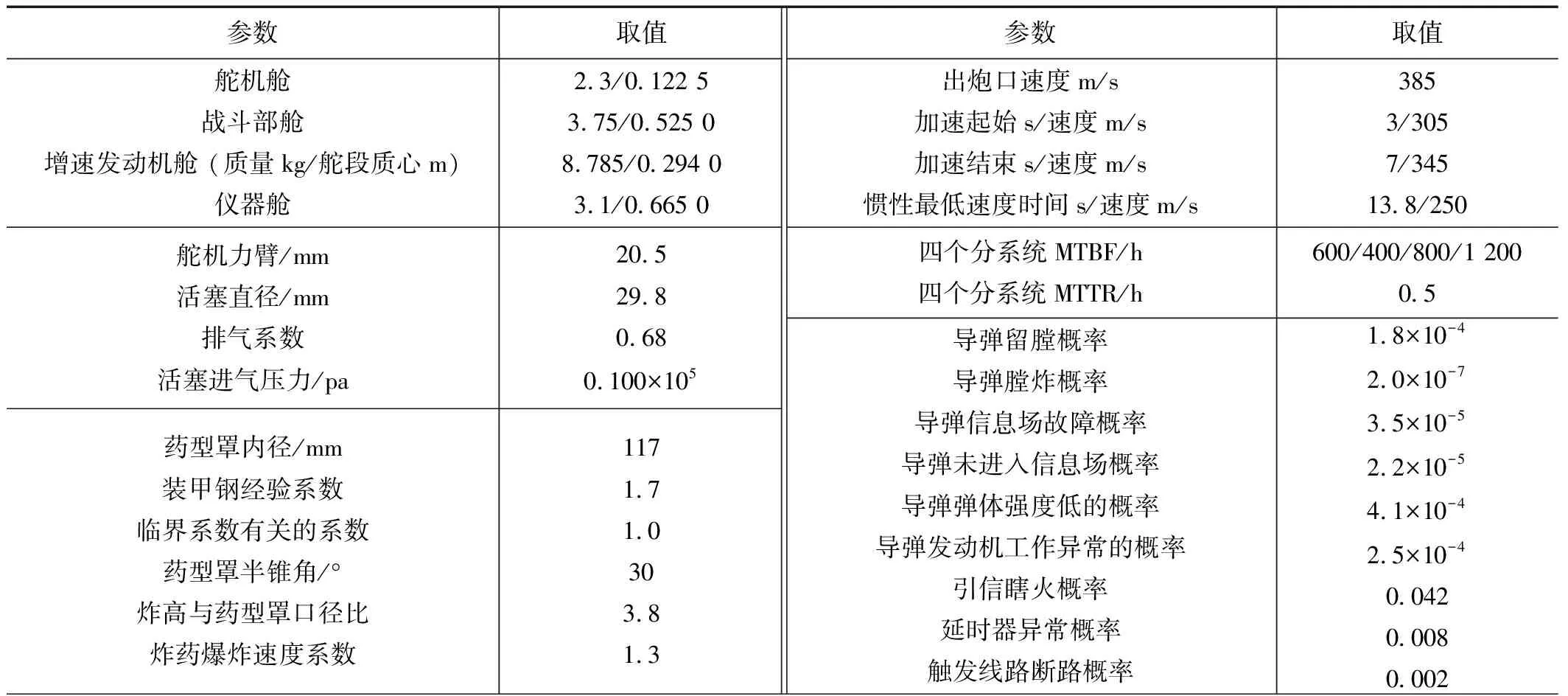
表1 APS05型125毫米激光架束炮射导弹系统的性能指标表

根据炮射导弹作战特点得知，在计算炮射导弹可用性时视为可修复系统，计算炮射导弹可信性时视为不可修复系统。

3.1 可用性向量计算

根据上述可用性向量数学模型以及系统性能指标计算可用性向量:

CM=0.99CN=0.99CP=0.99CG=0.99

a1=0.960a2=0.097a3=0.097a4=0.097

a5=0.097a6=0.009a7=0.009a8=0.009

a9=0.009a10=0.009a11=0.009

a12=0.000 009 9a13=0.000 009 9a14=0.000 009 9

a15=0.000 009 9a16=0

由此可得：

A=(0.960,0.097,0.097,0.097,0.097,0.009,0.009,

0.009,0.009,0.009,0.009,0.000 009 9,0.000 009 9,

0.000 009 9,0.000 009 9,0)

3.2 可信性矩阵计算

根据上述可信性矩阵数学模型以及系统性能指标计算发射可靠度、飞行可靠度与作用可靠度可信性矩阵：

DR=

DL=

3.3 固有能力矩阵计算

根据上述固有能力矩阵数学模型以及系统性能指标计算固有能力矩阵：

炮射导弹质心参数X=0.38；

炮射导弹射程参数S=4 358；

炮射导弹制导控制力矩参数M=0.097 227；

炮射导弹破甲深度参数P=750.232 5。

根据关于炮射导弹固有能力文献资料，从而设置μ1=0.3，μ2=0.2，μ3=0.25，μ4=0.25。

由此可得：

C=[0.134 2 0.259 9 0.187 4 0.185 6 0.259 9

0.362 9 0.359 4 0.517 7 0.259 2 0.373 3

0.369 7 0.502 0 0.716 0 0.723 0 0.516 3 0]T

3.4 系统效能计算

根据上述系统效能数学模型，可以得出炮射导弹系统效能，计算如下：

E=ADC=ADRC+ADIC+ADLC=

0.312 2+0.236 0+0.264 9=0.813 1

通过计算可知炮弹导弹系统效能大约为0.813 1，给定系统效能标准，如优等(0.85～1.0)、良好(0.70～0.85)、中等(0.55～0.70)、差等(0.20～0.55)以及劣等(0～0.20)。因此可以确定设计改进后的典型的APS05型125毫米激光架束炮射导弹系统效能为良好。

4 结束语

ADC方法可以将可用性、可信性和固有能力等通用质量特性综合成单一的系统效能度量，能够有效地反映炮射导弹系统的综合质量特性，成为研发与改进炮射导弹性能的重要依据。本文通过建立改进的ADC方法对炮射导弹系统进行了分析，使得ADC方法能够更精确地、有效地对炮射导弹系统进行全面评估。