山区高墩双塔斜拉桥约束体系研究
黄永福HUANG Yong-fu;李杰LI Jie;邹惠琼ZOU Hui-qiong;尹开川YIN Kai-chuan
(云南省交通规划设计研究院有限公司,昆明 650041)
0 引言
我国西部多为山区,地形地势复杂,地震烈度较高,给修建跨越山谷河流的桥梁建设带来较大的技术难题和施工风险。随着“一带一路”发展战略的推进和深入,西部地区作为陆上丝绸之路的必经之地,必须加速基础设施建设,带动地区社会经济,以适应国家发展战略。
斜拉桥作为典型的索结构桥梁,在200m~1000m跨度范围内具有较好的经济性。山区斜拉桥跨越深山峡谷,往往具有塔高和墩高的特点,导致结构的整体刚度小、主梁重心相对于墩底较高,给斜拉桥整体稳定性、抗震性能带来了极为不利的影响,如何提高整体刚度并减小结构地震响应关系着桥梁结构的安全。通过加大索塔截面尺寸,可以有限地增加整体刚度,一定程度上解决了稳定性问题,但带来的是建设成本的大幅上升和结构地震内力的增大,降低结构安全性。大量研究表明[1]~[4],选择合理适用的斜拉桥约束体系,是改善高塔斜拉桥稳定性、抗震性能最为直接和有效的措施。
斜拉桥常用的约束体系有[5]:①全漂浮体系,即索塔与主梁之间无任何约束装置;②半漂浮体系,索塔与主梁之间设置竖向支承,在纵桥向为自由状态;③固结体系,或称刚构体系,即塔墩梁固结;④支承体系,即塔梁固结,并支承于桥墩上。中等及大跨度斜拉桥多采用全漂浮体系或半漂浮体系,但由于山区斜拉桥墩高、结构柔的特点,这几种常规约束体系不能较好地满足大跨度斜拉桥的设计要求。
以一座典型山区高墩双塔斜拉桥为例,在常规约束体系的基础上,提出弹性约束体系,与半漂浮体系、单塔固定体系、双塔固定体系对比,通过结构稳定性能、抗震性能分析,验证弹性约束体系的合理性,为高塔斜拉桥约束体系选择提供参考。

图1双塔斜拉桥总体布置图(cm)
1 工程案例
该双塔斜拉桥主桥为(190+420+190)m双塔三跨钢混组合梁斜拉桥[6],边跨设置辅助墩,跨径组合为(62.4+127.6)m。主梁为由工字型钢纵梁、横梁、小纵梁、混凝土桥面板及连接件组成的格构式钢混组合梁,主梁全宽29m;斜拉索为扇形平行双索面,索面间距为26.5m,标准拉索间距为12.4m;索塔采用花瓶形索塔,由上塔柱、中塔柱、下塔柱、塔墩、上横梁、下横梁和群桩基础组成,两岸索塔高度分别为210m和250m。桥梁总体布置如图1所示。
为了综合评价半漂浮体系、单塔固定体系、双塔固定体系、弹性约束体系四种体系对于高塔斜拉桥受力的优劣,将从结构稳定性、抗震性能两个方面进行阐述与论证。
2 结构稳定性分析
斜拉桥的索塔、主梁承受着巨大的轴力和弯矩,在施工阶段和运营阶段可能出现失稳现象,稳定问题可分为第一类稳定(弹性稳定)和第二类稳定(非线性稳定),弹性稳定可以作为结构稳定性的初步评估。
弹性稳定是一种理想情况,当结构承受临界荷载时,若收到微小扰动,结构将丧失稳定,可能进入新的平衡状态。根据最小势能原理,弹性稳定在数学上可用以下平衡方程来表达:
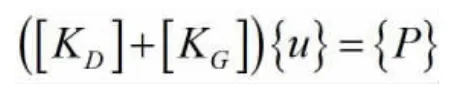
式中,[KD]为结构弹性刚度矩阵,[KG]为结构几何刚度矩阵,{u}为位移矩阵,{P}为荷载矩阵;当荷载达到临界荷载λ{P}时,几何刚度矩阵也增大λ倍,在微小扰动{△u}下,即便荷载λ{P}保持不变,仍然可保持临界平衡状态,于即有
因此,临界荷载系数λ在数学上变为求解特征值问题。
采用SAP2000有限元程序,建立空间计算模型,主梁、索塔、桥墩均采用梁单元模拟,斜拉索采用仅受拉桁架单元模拟;考虑成桥索力、主梁轴力、索塔轴力对结构刚度的影响(P-Delta效应);承台近似按刚体模拟,其质量堆聚在承台质心,承台底部固结;主梁压重、加劲肋等重量及二期恒载以点质量或线质量形式施加在主梁上;弹性约束两端锚固在主梁和索塔横梁上,单个索塔的弹性约束刚度取2×104kN/m,支座均按实际的固定或滑动模拟。四种约束体系弹性稳定分析结果如表1所示。
由表1结果可知,半飘浮体系纵向无约束,弹性稳定系数仅为4.58,虽然可以满足设计规范最小值4.0的要求,但结构刚度低,稳定性差,安全富余度太小;单塔固定、双塔固定或设置弹性约束后,弹性稳定系数有了明显的提升,对纵向刚度有较大的影响,能很好地满足设计规范要求。对于山区高墩双塔斜拉桥,建议采取纵向约束措施,提高桥梁整体稳定性能。
3 抗震性能分析
桥位区地震烈度为Ⅶ度,地震动加速度峰值为0.15g,场地类别为Ⅱ类。根据本桥场地地震安全性评价报告[7],主桥工程场地水平地震动参数见表2。
表2中,T1为设计反应谱第一拐点周期,T2为设计反应谱第二拐点周期,βmax为动力放大系数反应谱平台值,γ为设计反应谱下降段衰减指数,Cs为阻尼调整系数,Cd为场地系数,Amax为峰值加速度。
首先进行动力特性分析。采用Litz向量法进行特征值分析,取前300阶振型,通过计算,振型累积贡献系数达到99%以上。表3列出了各约束体系的前10阶振型的动力特性。
从表3中可以看出,由于四种体系在纵桥向采取了不同的约束方式,其动力特性主要的区别也表现在纵桥向。第一阶振型均为纵飘,半飘浮体系一阶周期为11.55s,为四种约束体系中最大值,因此结构刚度最小;双塔固定体系一阶周期为4.51s,为四种约束体系中最小值,因此结构刚度最大;弹性约束体系和单塔固定体系介于以上二者之间。
采用反应谱分析方法[8],振型组合采用CQC,方向组合采用SRSS,得到四种体系在50年2%概率水准下的地震响应。
从图2可知,双塔固定时,1号索塔剪力远大于其他工况,塔墩底达到1.68倍,塔柱底达到2.55倍,对1号索塔截面抗剪承载力要求大大提高;单塔固定时,2号索塔(即固定约束的索塔)索塔剪力远大于其他工况,塔墩底达到1.43倍,塔柱底达到2.17倍,对2号索塔截面抗剪承载力要求大大提高;弹性约束体系索塔内力比半飘浮体系大4%~17%,因此该弹性约束的设置对索塔内力影响较小,认为在可接受的范围内。

表1各约束体系稳定系数

表2工程场地水平地震动参数
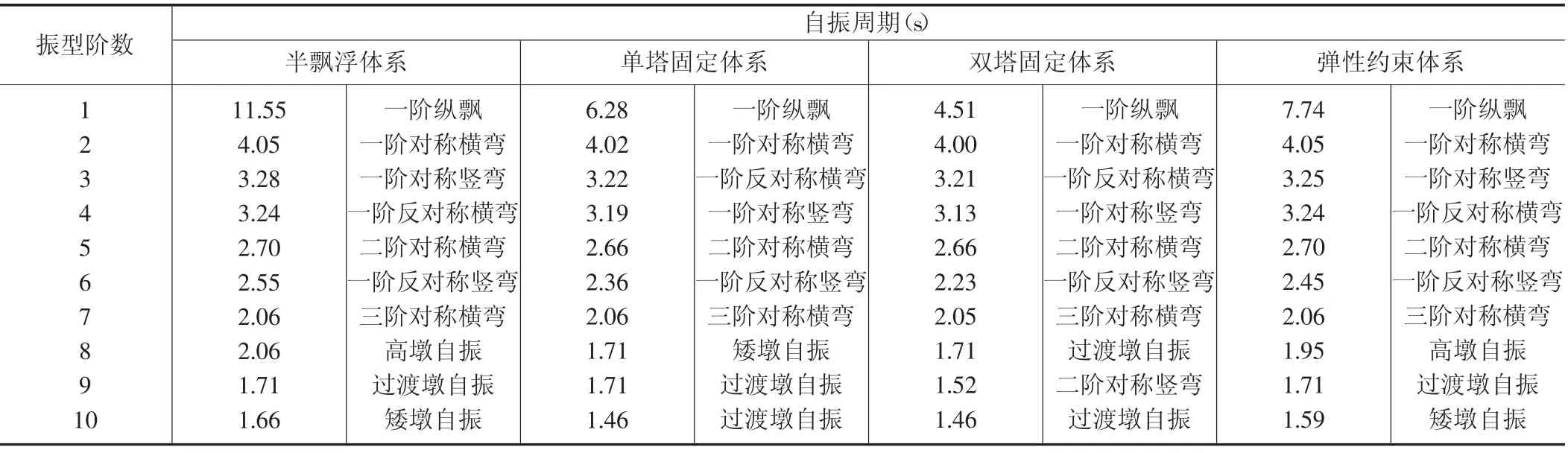
表3各约束体系动力特性
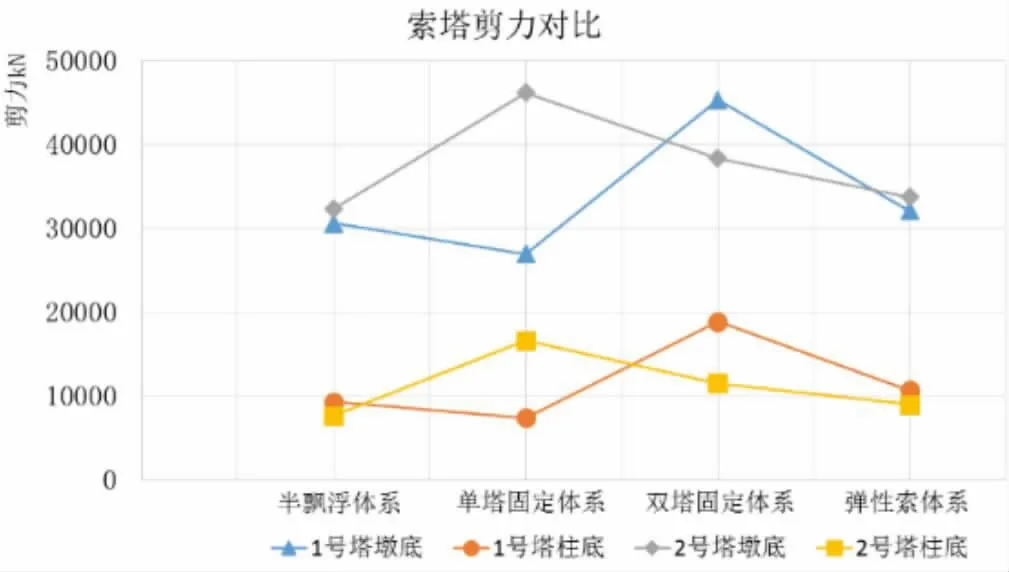
图2各约束体系索塔纵向剪力

图3各约束体系索塔纵向弯矩
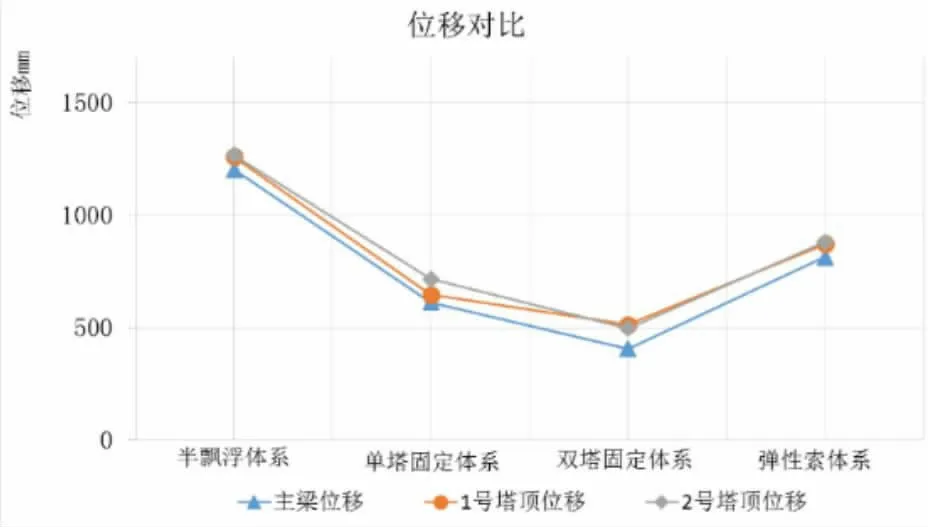
图4各约束体系索塔纵向弯矩
从图3可知,双塔固定时,1号索塔弯矩远大于其他工况,塔墩底达到2.23倍,塔柱底达到1.54倍,对1号索塔截面抗弯承载力要求大大提高;单塔固定时,2号索塔(即固定约束的索塔)索塔弯矩远大于其他工况,塔墩底达到1.79倍,塔柱底达到1.3倍,对2号索塔截面抗剪承载力要求大大提高;弹性约束体系索塔塔墩底内力与半飘浮体系基本相当,但塔柱弯矩减小了16%~22%。弹性约束将塔顶一部分地震力下放至塔梁交界处,减小了地震力传递的力臂,因此弯矩可能降低,实际分析结果与定性分析结论基本一致。总体而言,该弹性约束的设置对索塔抗弯计算有利。
从图4可知,双塔斜拉桥塔顶位移与主梁位移基本相当。半飘浮体系由于未设置纵向约束,塔和梁的纵向位移最大,达到双塔固定体系的3倍,为弹性约束体系的1.48倍,从结构动力特性分析也可推断出这一趋势。
此外,由于后三种体系设置了纵向约束,约束装置上将产生水平地震约束力。根据计算结果,单塔固定约束纵向剪力为19200kN,双塔固定约束纵向剪力为18850kN,弹性约束纵向力为5470kN。无论是单塔固定还是双塔固定,塔梁之间均产生了非常大的水平约束力,目前支座等装置的水平承载力很难满足受力需要,其次巨大的地震力将导致主梁钢结构及索塔横梁产生局部破坏,从而使得约束体系失效。
综上所述,单塔固定还是双塔固定产生了较大的索塔内力及约束装置地震力,实际工程中难以克服,因此均不是合理的约束体系;半飘浮体系在索塔内力方面表现良好,但产生了较大的纵向位移,梁端需设置大型伸缩缝,加上伸缩缝寿命较短,造价较高,后期维护成本不菲;而弹性约束既保证了索塔内力较优,又限制了梁端过大的位移,实现了力与位移的平衡。因此从结构抗震的角度,设置弹性约束是受力合理、经济性好的选择。
4 结语
通过结构稳定性能分析及抗震性能分析,设置纵向弹性约束有效地提高了桥梁整体稳定性能,提升了结构抗震性能,是山区高墩双塔斜拉桥结构体系的合理解决方案。

