可恢复退化下半导体激光器的可靠性研究
张东东,艾小川
(海军工程大学基础部,湖北 武汉 430033)
1 引 言
随着基础科学的飞速发展和各类稳定性高的稀有材料的应用,半导体激光器制造技术日益成熟,其体积小、效率高、功耗低等优良特性使其迅速成为光电子技术的核心器件[1]。目前半导体激光器广泛应用于材料加工、光纤通信、激光成像等高新技术的相关领域,由于半导体激光器为精密器件,工业生产对其精度有较高要求,故针对激光器的退化特点对其可靠性研究具有十分重要的现实意义[2-3]。
近年来,可靠性评估成为评判设备可用程度的有效手段,常见的评估方法是依据随机分布模型对设备的故障模式进行分析,利用数理统计的相关理论推算设备的可靠度。刘海康[4]利用贝叶斯推断和Weibull比例风险模型,解决了小样本下不同运行状况的电缆个体的可靠性分析;赵志草[5]根据Gamma退化过程的特性,提出了基于退化等效的共载表决系统的可靠性表达式。另一种评估方式是基于设备的退化数据,根据设备的退化路径,运用统计推断相关理论,得到设备可靠度模型; 蔡忠义[6]采用Wiener过程建立了隐含双重非线性退化模型,并利用现场检测数据,更新了隐含状态的后验分布;王强[7]针对战时装备受到使用退化与随机冲击的共同作用发生竞争失效的问题,提出了基于状态的预防性维修策略。
目前,基于数理统计的此类可靠性研究主要是采用竞争失效模型,利用自然老化与随机冲击的相关知识对设备的退化规律进行分析,但传统的模型只是对设备的自然退化规律和外界冲击类型进行了综合分析,并没有指出一些电子设备,尤其是软硬一体的设备存在的性能遭受冲击会部分恢复的情况。
本文基于半导体激光器设备的功能结构分析,根据设备的性能退化可恢复的特点,建立了基于竞争失效模型的可靠性模型,并对确定阈值和非确定阈值下的模型进行分析,最后利用数据实例对设备的性能退化特点进行分析,得到了可靠性变化的特点。
2 半导体激光器的性能退化因素分析
由于半导体激光器主要作为光电子器件应用于各类装备系统中,如工业上的激光打标机、军事领域的激光雷达,其在使用过程中会通过外接设备的软件系统进行精密控制,故其性能退化会受到软硬件的影响。其硬件退化主要表现为板级器件、电子元件和光学材料的老化,包括腔面老化、镀膜损耗、腐蚀等[8-10],这些由硬件退化导致的性能退化一般为不可恢复性退化,主要表现为性能随时间不断下降且不可逆。设备在工作中,软件运行同样会对其性能产生部分影响,工程中软件由于系统设计缺陷、病毒及非法操作问题对设备的性能产生影响,这些问题往往会导致软件在长时间运行和频繁开关时会产生卡顿等使得设备的性能呈现短时间的退化,但退化的性能会随着时间缓慢恢复。由此分析知,半导体激光器的退化存在明显的退化可恢复性。半导体激光器系统结构分析如图1所示。
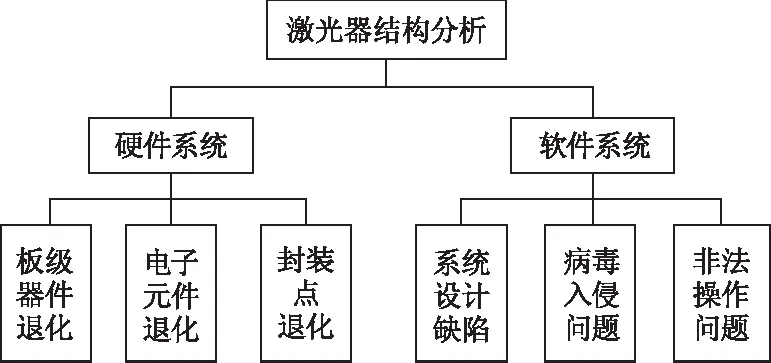
图1 半导体激光器系统结构分析
除此之外,半导体激光器的性能常常也会受到一些其他的因素影响,目前存在的可靠性理论的研究中把它定义为冲击,即设备在正常运行中会受到与工作无关或异常量的影响。冲击的发生使得设备的性能会发生迅速退化,激光器常见的冲击主要由环境应力、内部应力导致的,常见的外部冲击为高温冲击,内部应力冲击包括异常电流、载流子等冲击方式。根据光电子设备的工作特点,可以得知激光器在遭受异常电流、高温瞬时冲击时性能退化量会随着时间缓缓恢复,即激光器遭受冲击的退化是可恢复的,相关分析如图2所示。
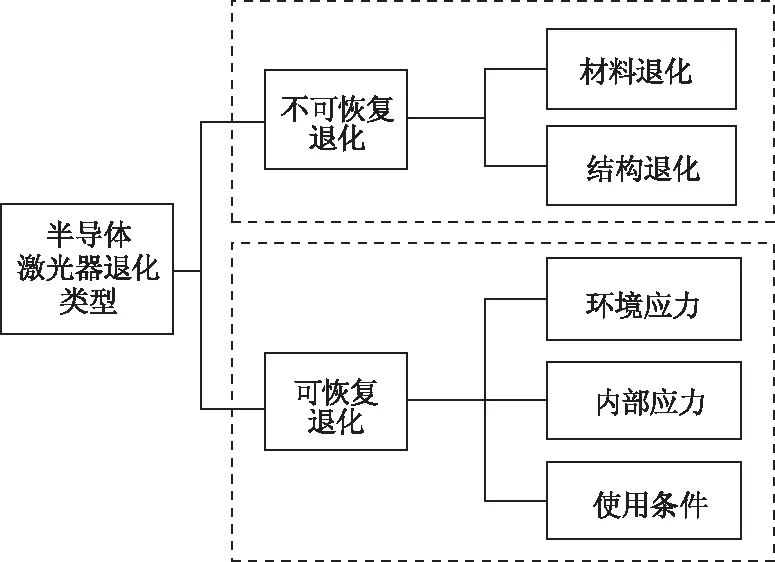
图2 半导体激光器的退化特征示意图
外接软件对激光器的影响规律比较难以描述,由于其对激光器的影响和冲击退化十分相似,性能退化量不会一直保持,而是随着时间缓慢恢复的,故本文将软件对设备的影响归为一类冲击。工程上,软件的长时间运行和操作不当会短暂的影响设备的性能,因此可以将其归为使用条件冲击。如图2所示,对于半导体激光器而言,其退化规律呈现出明显的可恢复退化和不可恢复退化的相竞争的规律,因此,本文基于其冲击退化的可恢复性建立了基于竞争失效理论的半导体激光器可靠度评估模型。
3 半导体激光器的退化过程分析
半导体激光器在工作过程中受到的冲击类型不同,其退化过程也不同,根据工程实际上装备性能退化特点,可以将退化类型分为可恢复退化和不可恢复退化。设备的自然老化过程为典型的不可恢复退化,其在工作过程中由于环境的腐蚀、电子板的老化等原因性能会随着时间缓慢退化,其退化证明为不可逆过程;然而,激光器的性能还会受到异常冲击的影响,本文主要研究半导体激光器遭受冲击时发生的可恢复性退化。
3.1 不可恢复退化机理
激光器发生的不可恢复退化为自然老化过程,考虑到Liu过程几乎所有的样本轨道都是Lipschit连续,故采用Liu过程来描述装备发生的不可恢复退化过程[11],不可恢复过程可表示为:
dX(t)=e+σdC(t)
(1)
方程描述的是一不确定的随机过程,C(t)为Liu过程,具有独立平稳增量,服从不确定正态分布N(0,t),为Lipschit连续退化过程,根据Liu在2009年建立的方程,令X(0)=0,可解得:
X(t)=et+σC(t)
(2)
X(t)表示t时刻性能的退化量,由此可以推得X(t)服从正态分布N(et,σ2t),其分布函数[12]为:
(3)
则若设备只发生自然老化,其退化量小于退化阈值d,产品不发生故障。此时,其可靠度为:
(4)
3.2 可恢复退化机理
半导体激光器在工作中会遭受各种类型的冲击(如图3所示),设备的性能会随着冲击的大小发生不同程度的退化,然而这种退化往往会随着装备稳定工作缓缓恢复,使得一段时间后装备呈现较轻的退化趋势。工程中常见的异常电流冲击和高温冲击等会使得装备短暂的发生较大的性能退化量,但随着电流电压恢复稳定,其退化量会缓慢恢复,直到达到一个新的稳定状态;激光器的运行往往离不开软件系统的支持,软件系统的卡顿、高频率刷新等其实可以视作对装备的硬件系统产生了不规律的冲击,这类冲击所导致的性能退化也是可恢复的。
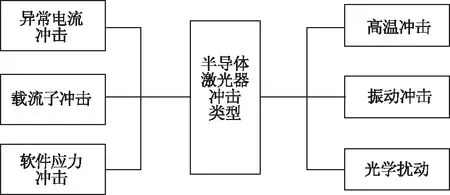
图3 激光器常见冲击类型
本文的可恢复冲击退化模型是基于累积冲击下的退化模型建立的,假设第j次冲击导致的退化量为Yj,为独立同分布的随机变量,Yj服从正态分布N(u,σ2),冲击过程服从参数为λ的Poisson过程,令tj表示第j次冲击到达的时刻,随机变量N(t)表示t时刻前装备遭受的总的冲击次数,故到t时刻为止,装备遭受冲击产生的退化量为:
(5)
根据冲击退化理论可以推得装备的退化量的分布为:
(6)
其中,F(t)为冲击时间间隔的分布函数;G(t)为Yj的分布函数。考虑到设备遭受冲击后,性能退化会出现短暂的峰值,且退化的性能与产品的性能退化量有关,设备的性能退化量越大,其恢复能力越小,直到设备达到新的平衡状态。因此,假设设备在受到冲击后,性能退化的恢复量Z(t)服从如下规律:
Zj(t)=(1-e-β(t-tj))Yj
(7)
其中,Yj表示装备在tj时刻的退化量;β为恢复系数,故Zj(t)实际上表示装备在遭受冲击发生性能退化后,在tj时刻到tj+1时刻之间的恢复规律,设备在两个冲击间隔内的恢复量为:
Zj=(1-e-β(tj+1-tj))Yj
(8)
因此,在t时刻时,设备因外部冲击导致的总退化量为:

-YN(t)(1-e-β(t-tj-1))

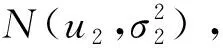
4 可靠度函数计算
4.1 确定阈值下的可靠度函数
假设半导体激光器在工作状态中,发生了多次冲击退化,总退化量为S1(t),由于:
(11)
(12)
(13)
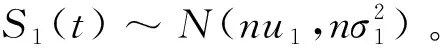
XS(t)=X(t)+S1(t)
YN(t)e-β(t-tj-1)
(14)
可以推得激光器在t时刻时的可靠度为:
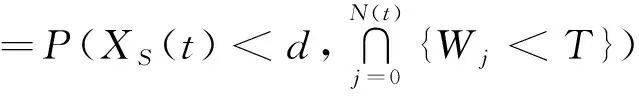
N(t)=j)P(N(t)=j)
(15)
根据公式(15)和式(11)分析得出,当λ为确定值时,恢复系数β越大设备的可靠度函数越大,其受到冲击时产品性能的恢复能力越大。若激光器遭受冲击后发生的性能退化不会恢复,其可靠度函数为:

(16)
4.2 非确定阈值下可靠度函数
在实际工程应用中,半导体激光器承受冲击不失效的能力会随着时间逐渐退化,故其冲击失效阈值是随着时间慢慢变化的,且设备性能退化越多,其抗冲击能力越弱。因此,假设设备的冲击失效阈值为线性衰减:
T(t)=T+kt
(17)
从式(17)可以明显看出冲击失效阈值为伴随时间线性衰减的变量,为了体现性能退化对阈值的影响,引入退化因子r(t)=ηS1(t),则修正后的冲击失效阈值为T(r(t))。这样,当设备遭受冲击时,不发生突发失效的概率为:
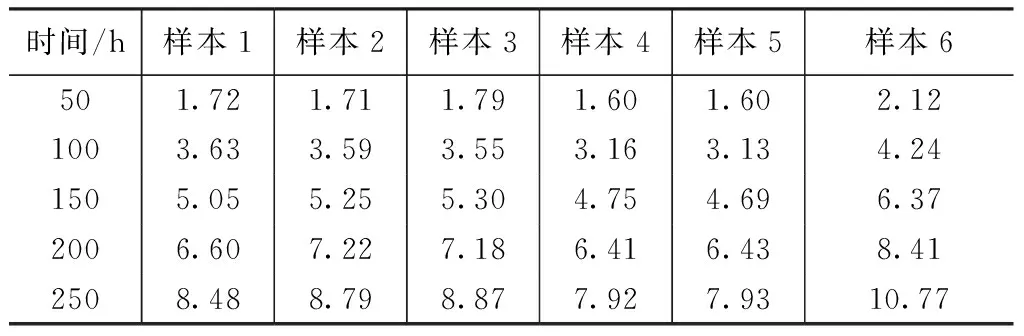
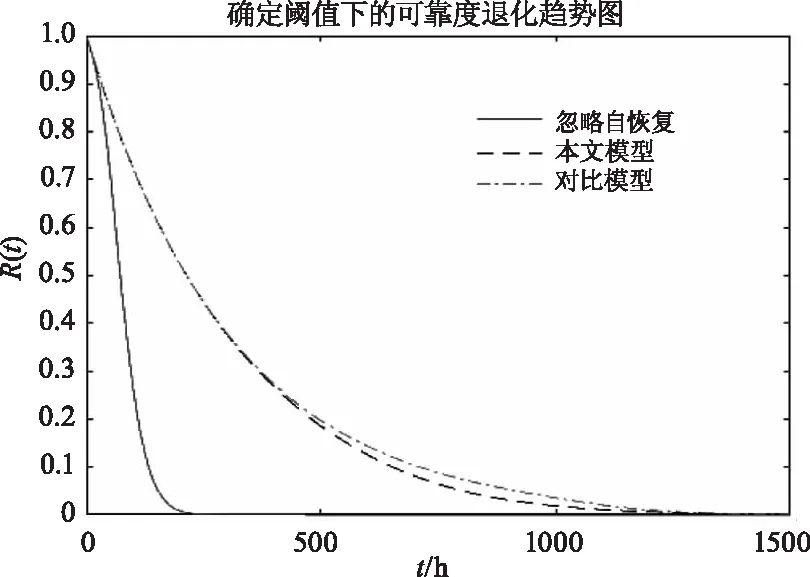
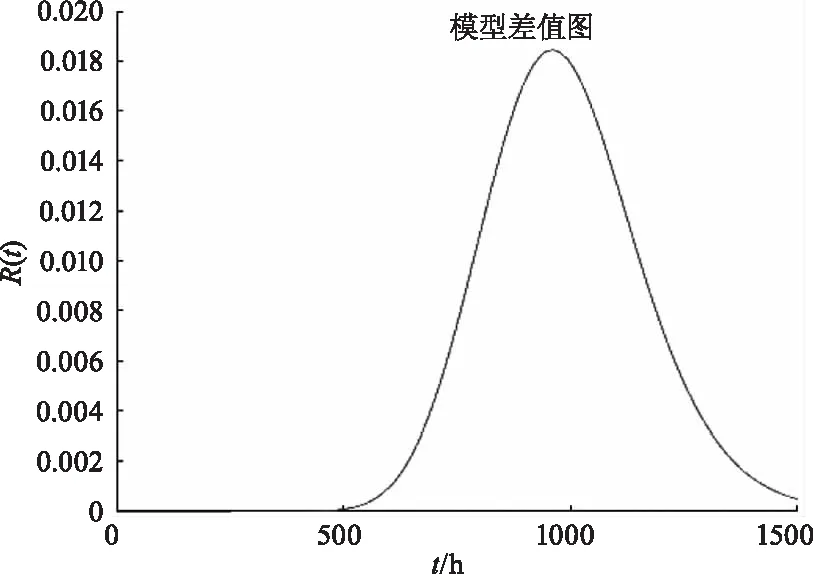
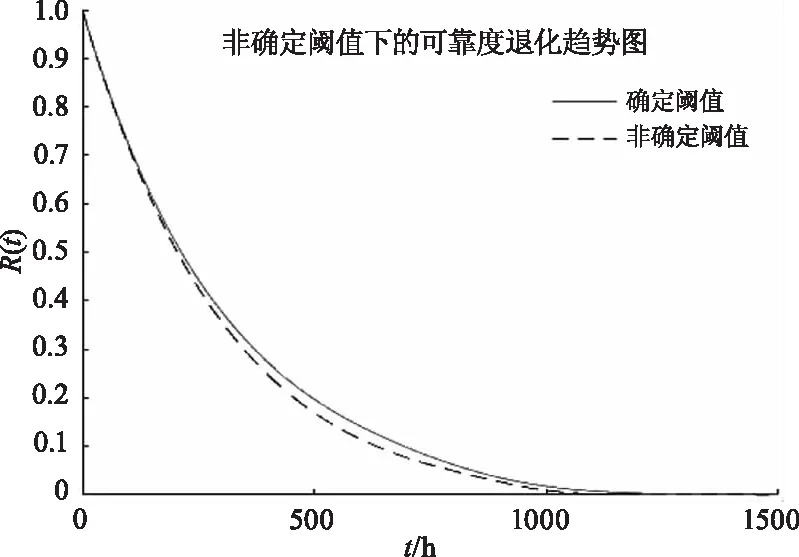
P(Wi =P(Wj-kηS1(t) (18) 则在t时刻,设备在相关失效阈值下的可靠度函数为: P(W1 (19) 半导体激光器是工业上常见的电子设备,常见的半导体的工作物质由砷化镓(GaAs)、硫化镉(CdS)等稀有材料,材料的退化和电子板的老化为其不可恢复退化的主要方式[13-14],在工作过程中,半导体激光器会不断遭受高温冲击,每次冲击均会造成其性能的短暂退化,故半导体激光器的退化模式符合本文所建立的模型。 根据文献[15]进行的半导体激光器的退化实验,实验主要分为两类,一类是无冲击的自然退化实验,自然退化即本文中的不可恢复退化,另一类是设备在遭受高温冲击后的冲击退化实验。设备正常工作时电流为16 mA,正常工作时室温为(23±2)℃,设备遭受的高温冲击幅值服从正态分布Wi~N(81.34 ℃,(11.74 ℃)2),冲击到达率λ=0.05/h,设定设备功率超过标准功率的50 %时设备即发生失效,即D=50,设备发生突发失效的冲击幅值为100 ℃。 表1是实验记录的激光器发生不可恢复退化时的退化数据。 表1 半导体自然退化部分数据(%) 根据Liu过程的相关理论,其期望和方差均是时间的线性函数,由于数据估计会存在误差,故假设设备的不可恢复退化的分布服从正态分布N(ut+ε1,σ2t+ε2),由实验数据进行估计可得自然退化分布为N(0.0351t+0.0058,0.0040t-0.2089),高温冲击导致的瞬时退化服从N(10.57,4.512),冲击到达率的平均估计值为λ=0.058 h,根据实验数据进行拟合可得半导体的恢复系数约为β=2。 基于实验所得数据及我们建立的模型,把文献[15]的模型作为对比模型,得到确定阈值下的可靠度退化趋势图图4、图5所示。 图4 确定阈值下的可靠度退化趋势图 图5 本文模型与对比模型差值图 由图4和图5分析得,忽略自恢复模型的设备在500 h内就发生了失效,然而根据实验数据,500 h时设备的性能退化量并未达到阈值,本文模型和对比模型的失效时间均在1000~1500 h内发生失效,与实验数据较为吻合。本文模型的失效时间在对比模型之前,从理论上分析可以得知,本文模型考虑的是设备性能发生冲击退化时会随时间部分退化,而文献[14]中考虑的是冲击时间间隔足够长性能会全部恢复,工程实际上,设备遭受冲击的种类和原因较为复杂,部分恢复较为贴合实际。 图6反映的是本文建立的确定阈值和非确定阈值下的可恢复退化模型,设备在工作过程中,随着性能不断退化,其承受冲击不发生突发失效的能力也越弱,故非确定阈值的可靠度小于确定阈值的可靠度,非确定阈值下的可靠度在后期比确定阈值下的可靠度退化更明显,比较贴合实际情况。 图6 非确定阈值下的可靠度退化趋势图 本文针对工程上半导体激光器的使用特点,对其退化规律进行深入分析后,将可恢复退化引入半导体可靠性研究,基于竞争失效模型建立了一类考虑设备遭受冲击时性能突变量会随着时间部分恢复的可靠度模型;并根据设备退化的实际特征,分析了突发失效阈值随着设备性能退化而变化的可靠度变化规律。根据实例计算结果,本文建立的模型能够有效的反应电子设备的可靠度变化规律,准确地预测设备失效的时间。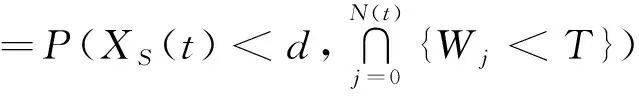
5 数值计算
5.1 案例说明
5.2 数据处理
6 结 论

