低压输出DC/DC正激变换器设计

石方园，李佳俊

（1．黑龙江科技大学电气与控制工程学院，黑龙江哈尔滨，150022；2．上海富山精密机械有限公司，上海，201500）

0 引言

隔离型DC/DC变换器是因为电路中加入高频变压器，使得前后级被电气隔离，这类变换器解决了输入输出压差大的问题，从而提高了供电的安全性和电磁兼容性[1]，较为常用的是反激和正激变换器，其中正激变换器在中功率场合有较为广泛的应用，然而单管正激变换器的开关管关断时所承受的压降为输入电压的2倍，对于输入电压较高的场合而言开关器件的选择较为困难，与此同时因为变压器内部的电感电流不能突变因而还需要磁复位绕组，进一步使得电路的设计较为复杂，为了实现低压大电流的功率输出本文设计并验证了一种双管正激变换器拓扑，此时电路中虽然多了一个开关管和二极管，但是却使开关管的关断压降的最大值降为输入电压，而且由于二极管的存在使得电路不在需要磁复位绕组[2-3]。

1 电路结构及工作原理

经典的双管正激变换器主电路拓扑如图1所示，主电路拓扑由高频变压器T、全控型开关器件Q1和 Q2，二极管 D1-4、滤波电感 L、滤波电容C1、负载 RL组成[4]。然而由于二极管通态电阻大，对于低压大电流输出时电路的损耗大，因而同步整流技术备受关注，其主要是利用电力开关管取代整流二极管，由于电力开关管的通态电阻小因而能够降低电路的损耗，根据工作原理的不同可分为电压型驱动与电流型驱动，其中电流型驱动需要设计复杂的电流互感器，而且磁复位绕组在复位时会产生很大电压尖峰，这使得二极管的电压应力增加不利于二极管选型，同时还是带来严重的EMI问题，相比之下电压型驱动不仅简单可靠，而且不存在死区期间二极管损耗问题，因而使用较为广泛，本文也采用了电压型驱动模式[5]，如图2所示。

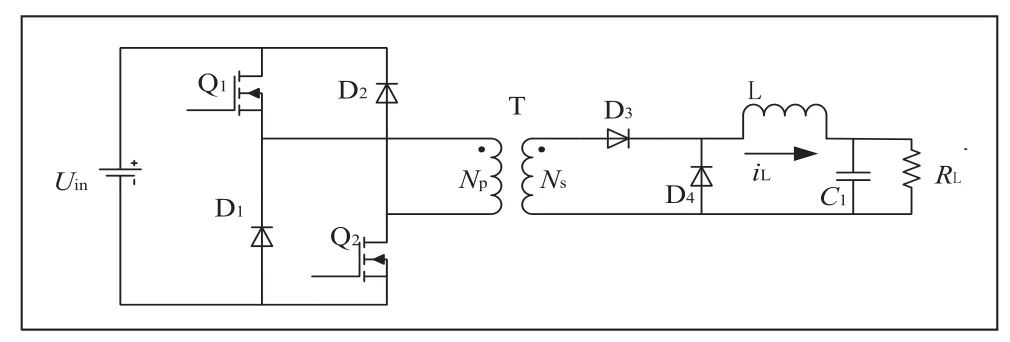
图1 双管正激拓扑

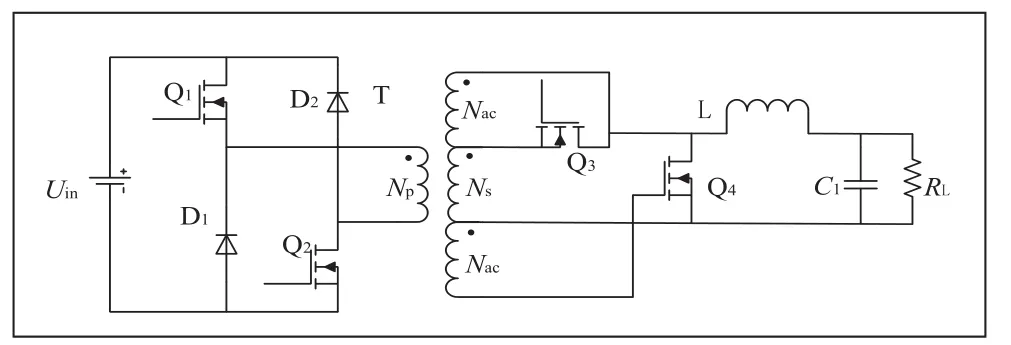
图2 同步整流拓扑

为方便下文分析现假设电路中所有的元器件均为理想元件，开关管Q1和Q2同时导通或者关断，图3是开关管Q1和Q2导通和关断的等效电路模型图，图4是电路的主要工作波形图[3]。

图3 等效电路

图4 主要波形

由3(a)可知，当Q1和Q2导通时，此时电源通过Q1和Q2变压器的原边将能量耦合到副边向负载端供电，此时电感进行储能，电感电流iL线性增加[6]。

由3(b)可知，当Q1和Q2关断时，由于电感电流无法突变，此时变压器原边中的能量无法通过副边向负载供电，只能通过二极管D1和D2将能量回馈给电源侧，因而相较于单管正激电路不需要磁复位绕组，此时电感对负载放电，则电感电流iL线性下降[6]。

2 主要器件计算分析

2.1 主变压器设计

主变压器选用的是EE40型号的磁芯材料，根据计算公式可知原边的计算匝数为：

式中VinMin——输入电压的最小值；

DMax——占空比的所取最大值；

Ae——EE40磁芯的有效截面积；

ΔBm——磁化曲线的磁摆幅；

f——功率器件的开关频率。

求出变压器的匝数比，考虑二极管的管压降Vf，则由公式(2)可求出匝数比：

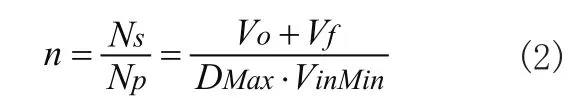
求得匝数比之后根据原边匝数则可算出副边匝数的数值，便根据需要取额定数值，同时将取副边匝数值再次代入到式(2)中，求出原边得匝数，并根据需要进行选择。

2.2 滤波电感计算

假定电感电流的波动为ΔIL，一般取输出电流的20%，电感电流的下降时间为(1-d)TS，电感值为L，由图4可得出ΔIL的计算公式为：

2.3 开关管参数设计

假定电感电流的波动为ΔIL，则由图4假定电感电流的峰值为iLPK则电感电流峰值的表达式如式(4)所示：

则流经开关管Q1、Q2电流最大值与电感电流的峰值相差一个变压器匝数比关系，即有：

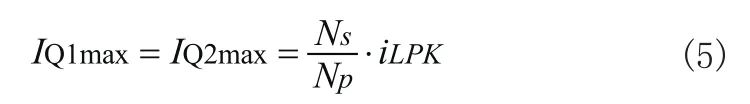
开关管Q1、Q2关断时承受的电压最大为输入电

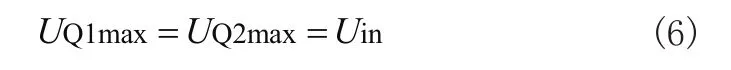
3 实验验证

利用SG3525搭建了一个小功率样机，在进行参数设定时考虑一定的裕量，具体的参数选取如下表1所示。

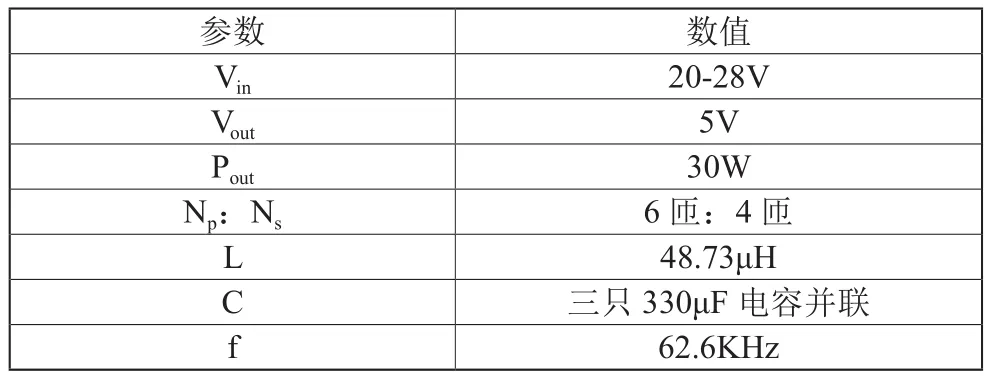
表1 参数设定

实验结果如下图所示，图5是开关管Q1电压应力UQ1，开关管导通时其大小等于输入电压，开关管关断时为为输入电压的一半，当原边磁复位完成之后其大小为零；图6为负载突变为额定时的输出电压波形，当负载接入时输出电压下降，但很快就又稳定在5V，即系统抗扰动能力较强；图7为变压器原边和副边的电压波形，两者图形一样，值大小存在一个匝数比的关系；图8为电感L两端的电压波形。

图5 开关管电压应力

图6 负载突变时输出电压波形

图7 变压器原边、副边电压

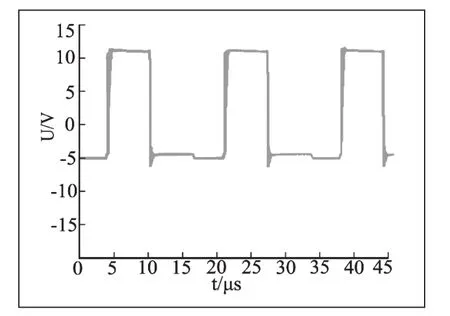
图8 电感电压波形

4 结论

本文主要论述了双管正激变换器电路的工作原理，对其中一些主要器件参数完成了计算推导，通过小功率实验样机验证了所设计的双管正激变换器具有良好的动态特性。