新能源风光发电功率预测模型分析

孔宏鑫

（浙江温岭东海塘风力发电有限公司，浙江温岭，317500）

0 引言

随着当前全球气候变暖以及传统能源应用过程中所带来的一系列问题日渐严重，人们开始寻找能够代替传统能源的新型能源，而风能发电与光伏发电作为清洁的可再生能源因其优秀的特点而得到了各个国家地区的青睐，从而得到了大力的开发以及利用。

风能在全球已探明的蕴含量大约有2.74×109MW，而其中能够被有效利用的风能则大约占总风能的0.74%[1]。自各个国家地区加大对于风能的开发利用后，全球的风力发电总量至2010年已达1.6×105MW，而随着风能发电技术的日渐成熟以及各国之间环保意识的加强，风力发电将在商业竞争力方面极大地超过传统的发电模式。除风能发电以外，光伏发电以其灵活环保的特性而在当前全球能源应用行列中逐渐发挥非常重要的作用[2]。基于风力发电以及光伏发电的特点以及未来的发展趋势，为了弥补其单独应用过程中存在的不足，有效结合二者优点的风光发电系统逐渐开始推广，但是在实际应用过程中，其仍存在着一些问题需要解决。基于此，本文结合风能发电以及光伏发电的特性来对基于RBF神经网络的风光发电功率预测模型进行分析，从而为其应用过程中所存问题的优化解决提供思路。

1 风力发电的统计规律研究

风力发电过程中，其主要受到风速以及风向的影响，因此本节分别对风速以及风向的统计规律进行简单介绍。

风速主要是指单位时间内空气在水平方向上移动的距离，不同的时间长度下风速具有不同的变化规律，而造成这种变化规律差异化的原因主要是不同的地形地貌、海陆分布差异以及不同的季度气候影响[3]。以我国为例，我国一般春季风速较大，而夏季风速却相对较小。除了不同季度背景下风速不同外，一天内白天与晚上的风速也并不相同，通常情况下白天风速较大，而凌晨与晚上的风速则最小，其分界点一般为下午的六点至七点之间。

风向主要是指风吹来的方向，其通常由十六个方位来进行表示，同时为了能够便于统计以及表述，人们也常用角度来表示，例如以正北为标点，顺时针方向依次为90°东风、180°南风、270°西风以及360°北风。

2 光伏发电的统计规律研究

本文主要通过对光伏发电系统的发电原理进行简要介绍来对光伏发电的统计规律进行研究。光伏发电主要是通过太阳能电池来将太阳能直接转换为电能，因此其系统主要由太阳能电池、逆变器、控制器以及蓄电池等部件构成。当前所用的太阳能电池主要是利用光伏效应来将太阳光能转换成为电能，而由于半导体P-N结的光伏效应比其他材质结构的光伏效应更加明显，故当前常用的太阳能电池皆由半导体制成，其工作原理为：当P-N结上的P型硅与N型硅结合时，N型区的电子会迅速扩散至P型区，而P型区的空穴则会迅速扩散至N型区，此时P型硅带负电，N型硅带正电，半导体硅的内部便会形成电场。当太阳光照射在半导体上时其内部会形成新的空穴-电子对，同时在P-N结电场作用下，半导体硅内部的电子便会由P型区转移至N型区，接通电路后，便会形成电流。但是，只要在空穴与电子结合前利用电场作用将其进行分离，便能够产生可测试电压[4]。

3 基于RBF神经网络的风光发电功率预测模型

为了能够有效发挥风力发电以及光伏发电的优点，并且最大限度避免当前风光发电系统应用过程中所存在的包括预测难度大以及难以有效控制等在内的问题，本文对当前应用较为广泛的基于RBF神经网络的风光发电功率预测模型进行分析，以期实现对风力以及光伏发电功率准确合理的预测。

3.1 RBF神经网络的基本结构

RBF神经网络作为一种前向神经网络，其结构往往与多层前向型网络相类似，即主要由输入层、隐含层以及输出层组成。其输入层一般由信号源节点构成，隐含层内神经元的径向基函数与以往的全局响应函数不同，是一种中心点径对称且衰减的局部响应函数，而输入层作为RBF神经网络的第三层，主要负责对输入层下的输入模式进行响应[5]。

通常情况下RBF神经网络的函数传递模式有两种，分别是径向对称函数和高斯函数，径向对称函数的关系表达式如下所示：

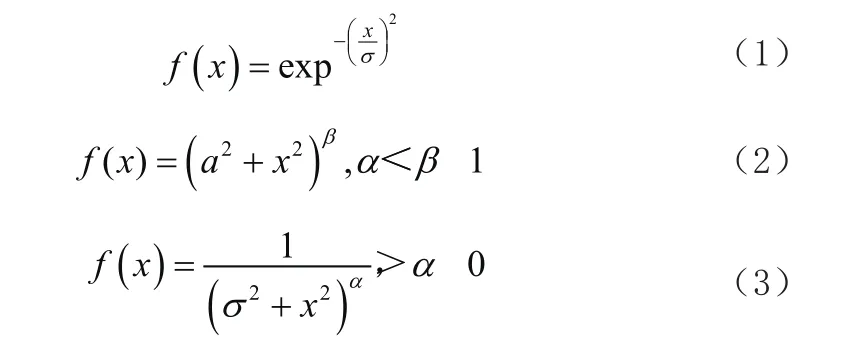
但是在实际应用期间，上述函数关系式的频率不高，而高斯函数的应用几率最大。高斯函数的关系表达式如下所示：

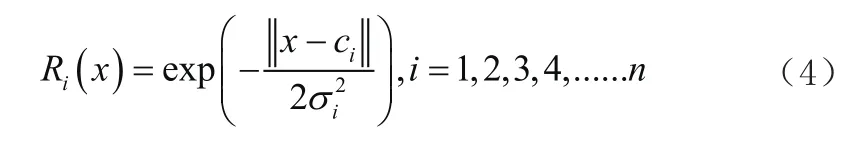
在公式中，ci表示第i个基函数中心，n维输入向量由x表示，在函数关系式中，n维输入向量和第i个基函数中心的向量的维数相同。σi在函数关系时中表示感知变量，其结果对基函数围绕中心点的宽度值有着决定性影响。隐藏层节点数又被称作为感知单元个数，在公式中由n表示。表示两者之间的距离大小。在ci位置，Ri(x)具有唯一性，且是最大取值，但是当x和ci两者之间的距离增加时，Ri(x)将会随之下降，直至结果为0。若是输入值确定，想要激活，就只能凭借临近与n维输入向量的一小部分。

研究RBF神经网络期间，传递函数若是选择应用高斯函数，那么隐藏层将会实现从X到Ri(X)的非线性映射，输入层将会实现由Ri(X) 到yk的线性映射。在此假设输入层的输入为 ：X=（x1，x2，x3，……，xn），输出层的输出为 ：Y（y1，y2，y3，……，yp），那么此时输出层的第k个神经元网络的输出结果关系表达式如下所示：

公式中，输出层节点为p，输入层节点数为n，隐藏层节点数为m，在隐藏层当中的第i个和第k个神经元进行连接是，其权值表示为ωik。所以，当明确连接权值和聚类中心以后，可以对输入的RBF神经网络所对应的输出值进行计算。

3.2 模型样本的归一化处理

为了对风光发电功率进行有效的预测，需要在预测过程中采集一定量的样本来进行分析，但是由于相关样本指标分量的单位并不相同，往往会导致预测数值具有相对较大的差异化，因此需要对指标分量进行归一化处理，从而有效降低数值差异化对预测结果的影响，其主要包括风向以及温度的归一化处理。

由于风向的度数主要以360°圆周作为参考基准，因此通常将正北方向确定为0°，然后取风向的余弦值和正弦值来作为风向的归一化数值[6]。而温度的归一化过程为了保证数值的准确性，通常利用如下公式进行归一化：

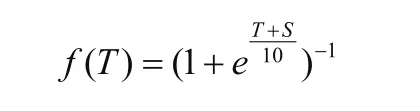
其中T为温度值，f(T)为温度归一化处理后的数值。

3.3 基于Matlab构建RBF神经网络模型

Matlab主要功能是处理图形图像和信号、进行数学矩阵运算和各类数据分析的数学软件，利用Matlab软件，可以为新能源风光发电功率预测模型构建所需要的数据分析提供帮助。在Matlab软件的工具箱中，其所提供的radbas函数为径向基传递函数，通过利用该函数值可以将神经元输出，在输入时，其内容主要为权值矢量和输入矢量两者距离之和，再与阈值相乘得到的结果。Matlab软件工具箱中的newrb函数为径向基设计函数，在对函数进行调用的时候，其调取程序为net=newrb（P,T,goal,spread,MN,DF）。在逼近函数时选择应用径向基函数网络，此时newrb每发生一次迭代，将会使得径向基网络隐藏层神经元增加，直至神经元的数量达到最大值，或者是符合均方误差。例如，在一个具有10个隐藏层神经元的网络模型设计期间，其调取程序如下：

RBF神经网络在Matlab中，通过使用函数sim()实现仿真处理，在函数调用的时候，其调用程序为[Y,Pf,Af,E,perf]=sim(net,P,Pi,Ai,T)。

3.4 RBF神经网络的层次设计

基于RBF神经网络的风光发电功率预测模型的层次设计主要包括三方面，即输入量的选择、隐含层节点的确定以及输出层节点的确定。由于风力发电功率往往受到风力、风向以及温度的影响，而光伏发电功率主要受光照强度、天气类型以及温度的影响，因此该模型的数量需要选择对模型预测值影响较大，但是不同输入量之间影响却相对较小的数据，例如光伏发电功率预测模型只需将光照强度和温度作为输入量即可。

RBF神经网络中隐含节点的确定关系到其网络性能是否可以满足实际需求，以往所采用的使隐含层内神经元数目与输入向量的元素数目保持一致的处理方法并不可靠，因此经过分析选定风力发电功率预测模型的隐含层的节点数目为12，而光伏发电功率预测模型的隐含层节点数目为9。

而对于输入层节点的确定而言，为了保证预测结果的准确合理，风光发电功率预测模型的输出通常选定为风力发电与光伏发电二者的预测时间节点的实际功率值。

3.5 预测结果分析

按照使用的目的不同划分数据样本类型，一类为测试模型用数据，一类为训练模型用数据。获取某地区24h之内的风速、风向、大气平均温度值、天气情况以及太阳辐射强度等信息。根据需求构建模型，可以显著提升预测精准度。

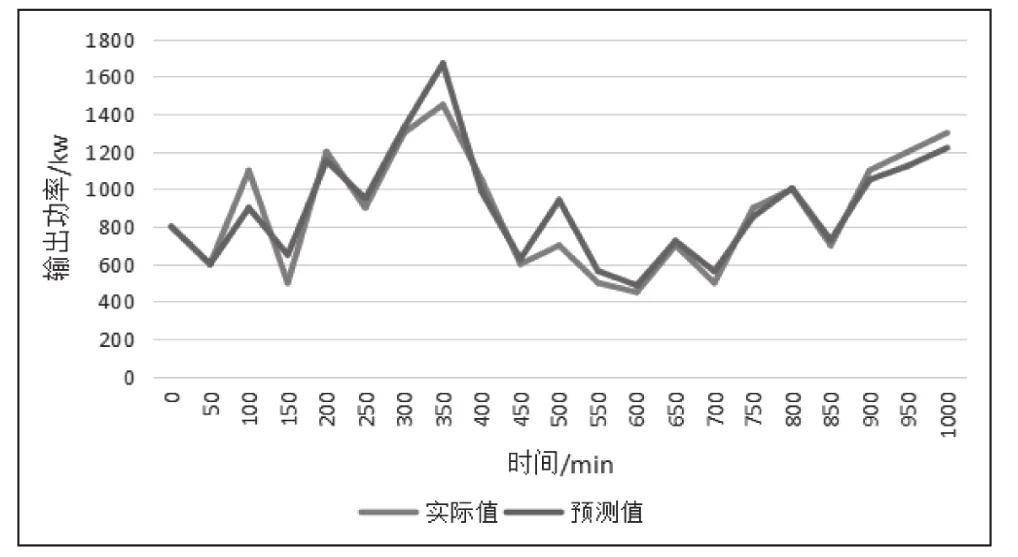
图1 风力发电功率对比图

4 结语

新能源的开发以及广泛利用是当前为了有效解决传统能源的存储量逐渐枯竭以及其所带来的的一系列的污染问题而提出的新的能源方案，其能够有效满足资源可持续发展的需求。而风光发电由于其自身所具备的优良特性而逐渐在新能源发展过程中占据了重要的地位，但是风光发电在实际应用过程中存在着预测难度较大以及资源调度困难等问题，需要对发电功率进行有效预测。因此本文对风光发电进行了简单介绍，同时也就基于RBF神经网络的新能源风光发电功率预测模型进行了叙述分析，从而可以为当前风光发电的电力调度以及与其相关的各类工作安排提供合理的决策支持。