在S2局部坐标下的二维不可压Naiver-Stokes方程

李小如, 王 术, 耿 范

(广州大学 数学与信息科学学院, 广东 广州 510006)

0 引 言

Naiver-Stokes方程组是流体力学方程组中的典型代表, 在物理工程学、等离子物理、半导体物理、航空航天、空气动力学、血液动力学和科学计算等诸多领域都有着广泛的应用。它可以对气流、大气洋流、管道中的流体血液等各种各样的液体流动进行建模。对简化或者具体表达形式的Naiver-Stokes方程组的研究, 可以更好地应用于天气预测、防止环境污染、提高各种交通工具的性能和在医疗上辅助治疗心血管疾病等[1]。

在R3中有如下形式的Naiver-Stokes方程组：

(1)

式中，u(x,t)表示未知的速度场,p(x,t)表示未知的压力,u0(x)表示给定的初始速度场, 且在分布的意义下满足∇·u0=0,μ是粘性系数。

至今, 其数学理论的研究备受关注, 它是国际数学界长期关注的焦点问题之一。迄今为止, 在三维情况下, 虽然已经有很多重要的结果, 但是方程组(1)的Leray-Hopf整体弱解的正则性仍不清楚, 目前仍然是流体力学理论中的公开问题, 美国Clay数学研究所也在2000年把三维不可压缩Naiver-Stokes方程具有有限能量光滑初值整体正则解的存在性或在有限时间内爆破列为7个“千禧问题”之一。近些年来, 有越来越多的研究者研究曲线坐标系下的Naiver-Stokes方程组的一些性质及其弱解的估计或全局解等相关内容, 也取得了重大的进展[1-4]。

1 二维流形S2上的Naiver-Stokes方程

数学的发展促使微积分从欧氏空间到微分流形的拓展,而欧氏空间是最简单的光滑流形, 它的微分算子在局部坐标下的表达式可适用于一般的黎曼流形。为了计算简便, 考虑低维流形即二维流形S2在局部坐标下的微分算子。

首先在S2上建立坐标系, 即建立球面和平面或平面一部分的一个对应。由于球面具有紧致性, 而平面是非紧致的, 则这样整体的坐标系是不存在的, 故考虑局部坐标。然后利用局部坐标分别表示出二维流形S2上的梯度算子、散度算子以及拉普拉斯算子, 进而写出Naiver-Stokes方程组的具体形式。

R3中的单位曲面S2(1)={(x,y,z)∈R3|x2+y2+z2=1}是二维黎曼流形(S2,g), 则它的参数方程表示为

x=sinθcosφ,y=sinθsinφ,z=cosθ

(2)

其中,0<θ<π, 0<φ<2π,g是黎曼度量。

命题1假设u(θ,φ,t)是二维Naiver-Stokes方程未知的速度场, 则在u=uθeθ+uφeφ时, 在S2局部坐标系下的Naiver-Stokes方程可以表示成如下形式：

其中,

证明证明分3个步骤。

(1)计算黎曼度量

通过2种方法引入黎曼度量g, 一种是球极投影引入黎曼度量(或者是通过欧氏空间诱导在球面上的度量), 另一种是曲面在局部坐标系下的第一基本形式, 而这2种方法算出的黎曼度量是一致的。

(3)

不难看出

(4)

考虑变量θ,φ的一阶偏导数

(5)

其中,

(6)

若在局部坐标系(U,ξi)下, 则S2(1)的黎曼度量g的表达式为

(7)

(8)

先将ξ1,ξ2代入式(8), 再结合式(6)可进一步计算出

g=dθdθ+sin2θdφdφ

(9)

则度量系数分别为

g11=1,g12=g21=0,g22=sin2θ

(10)

故有g的反变分量gij(即gij的逆)为

(11)

则度量系数的行列式为

(12)

方法2: 通过考虑R3中的正则曲面, 利用曲面的第一基本形式。记

r=(sinθcosφ,sinθsinφ,cosθ)

(13)

(θ,φ)是S2中的局部坐标, 由方法1中的描述可知,r是浸入R3中的二维光滑子流形。

令

E=,F=,O=

(14)

ds2=dr,dr=(dθ)2+

E(dθ)2+Fdθdφ+O(dφ)2

(15)

由于

(16)

则将式(16)代入式(15), 有

E=1,F=0,O=sin2θ, ds2=(dθ)2+sin2θ(dφ)2

(17)

由i≠j时,gij=0, 故有度量系数分别为g11=1,g12=g21=0,g22=sin2θ且

(18)

(2)计算单位正交切向量

下面是单位正交标架场的算法[7], 设(U,ξi)是M的一个局部坐标系, 黎曼度量g在该坐标系下的分量为

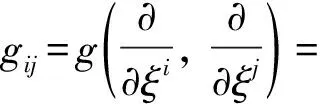
(19)

其中,ξ1=θ,ξ2=φ。

(20)

a1,eθ=0

(21)

由此可知

λ=-

(22)

即得

(23)

将a1单位化并记为eφ, 则

(24)

(3)考虑流形上的3个微分算子[6-9], 进而得到Naiver-Stokes方程组的具体表达式

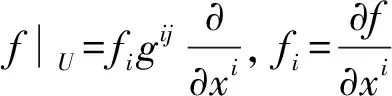
(25)

(26)

(27)

令u=uθeθ+uφeφ, 则对应的梯度算子、拉普拉斯算子及散度算子分别为

(28)

(29)

(30)

这里应用了逆变分量uθ,uφ与物理分量uθ,uφ之间的关系。

结合式(28)～(29), 可分别计算出u·∇u, Δu。

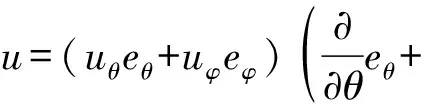
(31)

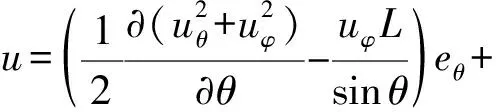
(32)

(33)

且压力的梯度与速度场对时间的偏导数分别记为

(34)

由上述表达式(32)～(34), 可以得到在二维流形S2局部坐标系表示的Naiver-Stokes方程如下：

(35)

其中,

(36)

(37)

命题证毕。

为进一步研究二维流形S2局部坐标系表示的Naiver-Stokes方程, 需考虑边界条件。R3中半径为r=1的标准单位球面S2(1)是截曲率为c=1的二维空间形式。S2(1)是单连通且紧致的, 因而又是完备的。

因为球面是二维封闭的曲面, 但二维的封闭曲面是没有边界的，所以为了得到边界的条件,可以考虑球面的上半球面来进行研究, 因为上半球面是一个有边界区域。

在R3中考虑S2(1)球面的上半球面：

从而, 对于上半球面的参数方程可写成

系统(35)的初始条件和边界条件可分别写成:

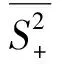
2 能量等式验证

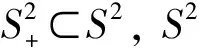
(38)

结合笛卡尔坐标下二维Naiver-Stokes方程的能量等式的计算步骤：

首先根据ut+(u·∇)u+∇p=μΔu, 将其与u作内积, 并进行分部积分, 可得

则对于任意的0≤t≤T, 有下述的能量等式：

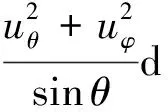
其中，dτ=dθdφ,

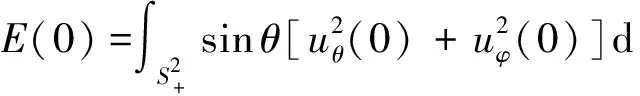
证明先考虑式(38)中的第一个等式, 让它与sinθuθ作内积, 并用格林公式进行分部积分, 则可得

(39)

然后再考虑式(38)中的第二个等式, 让它与sinθuφ作内积, 并用格林公式进行分部积分, 则可得

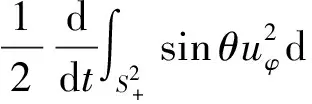
(40)

又因为不可压缩条件：

(41)

将式(41)与sinθuθ作内积, 则有

再用格林公式进行分部积分, 故可以得到

即有

(42)

将式(39)～(40)两个等式相加, 并将式(41)～(42)代入其中, 可得

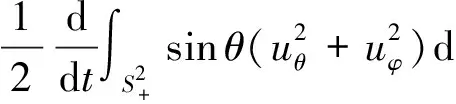
即

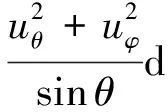
其中,

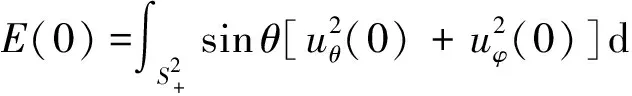
即完成能量等式的证明。

3 结束语

Naiver-Stokes方程在流体力学中具有重要的理论价值, 本文主要是对几个微分算子从欧氏空间到流形的推广, 并给出了详细的计算过程, 进一步得到了Naiver-Stokes方程在S2中局部坐标下的具体表达形式, 这有利于对流体的局部形式进行了解, 并可以进一步对Naiver-Stokes方程在流形上局部坐标下解的适定性进行分析, 这对于研究方程的解具有重要的意义。因此, 可以从这样的坐标系出发, 突破更多有关于解的问题。