某连续式超声速风洞控制系统设计研究

陈旦, 王众, 鲁相, 林辰龙, 裴海涛

(中国空气动力研究与发展中心 设备设计及测试技术研究所, 四川 绵阳 621000)

某连续式超声速风洞作为国内首座连续式超声速风洞，马赫数范围为1.5～4.5(目前马赫数只到3.0)，压力范围20～200 kPa(绝压)。风洞由多级压缩机驱动，配置有喷管段、试验段和超扩段等部段，同时配置总压系统实现增压和降压运行，配置换热器段实现总温调节。

目前国内超声速风洞均为暂冲式，代表性的为中国空气动力研究与发展中心的2 m超声速风洞。相比暂冲式超声速风洞，连续式超声速风洞单次运行时间长，流场参数控制精度高，运行效率高，可在较低速压下运行，且连续式超声速风洞启动/关车时冲击小，降低了对模型、天平等机构强度的要求。该风洞的建设将填补国内连续式超声速风洞领域的空白，并通过摸索其运行控制及设计、调试关键技术，可为今后更大量级的连续式超声速风洞的建设调试奠定基础。

我国第一座跨超声速风洞是建于1958年的FL-1暂冲式风洞，目前最大的为2 m超声速暂冲式风洞，其马赫数范围1.5～4.0，马赫数均匀性0.003 3～0.006 2，总压范围100～1 200 kPa，总压控制精度0.3%[1-2]。国外早在1960年就建立了大型连续式超声速风洞，尺寸最大的为美国阿诺德工程发展中心的16S风洞(建成于1960年)，其口径达到4.9 m，马赫数范围为1.5～4.75(并论证过马赫数6及以上实施的可能性)，高度模拟范围为15～45 km[3]。过去几十年受连续式超声速风洞建设费用等影响，国内外多以暂冲式风洞建设为主，但最近一二十年，由于连续式超声速风洞的优异性能以及发展高超声速武器的紧迫性，又加大了对连续式超声速风洞的建设投入，比如美国于2013至2015年对封存的16S风洞开展了状态评估，之后更是进行了耗资6 000万美元的修复和现代化改造[4-6]。

目前，国内外文献对连续式超声速风洞控制系统的设计研究描述极少，即使是关于连续式跨声速风洞控制系统设计调试的文献也相对较少[7-15]。美国NTF跨声速风洞(总压100～830 kPa，马赫数0.1～1.2)最近几年利用二喉道精调来提高马赫数稳定性；中国空气动力研究与发展中心的0.6 m连续式跨声速风洞(下简称0.6 m风洞)通过设置内环观测阈值的串级控制加模糊PID的控制方法，采用转速粗调加中心体精调的方式，实现马赫数控制精度达到0.001，并通过分段变参数模糊PID控制算法实现了常压/增压下总压控制精度0.1%(负压下0.2%)；西北工业大学NF-6跨声速风洞采用转速加栅指及其组合的方式实现了马赫数控制精度0.002。

考虑到连续式超声速风洞流场建立方式和(低)跨声速风洞不同，且风洞马赫数更高，气动载荷更大，压缩机功率更高，风洞总压和马赫数等参数仍存在相互耦合，因此，如何实现流场参数的精确控制和快速稳定是控制系统设计中的关键技术问题。

1 流场参数控制原理

某连续式超声速风洞启动运行后，换热器系统按照一定的冷量运行，即总温不做精确控制，因此，本文讨论的流场参数特指总压和马赫数。总压和马赫数控制是一个复杂的综合性任务，需要调动其下属的各个子系统协调运行，其原理如图1所示。首先由核心控制器(BOXPC)通过调度喷管/超扩段控制系统调节型面/调节片至对应的马赫数，然后通过压缩机控制系统对压缩机级数以及转速进行控制来建立风洞运行压比，并实现马赫数控制；通过对总压系统调节阀或真空泵等闭环控制实现总压的精确调节；通过模型姿态系统实现模型迎角等调节；通过标准参数测量系统实现总压和马赫数参数的测量，并作为总压和马赫数控制的基准。

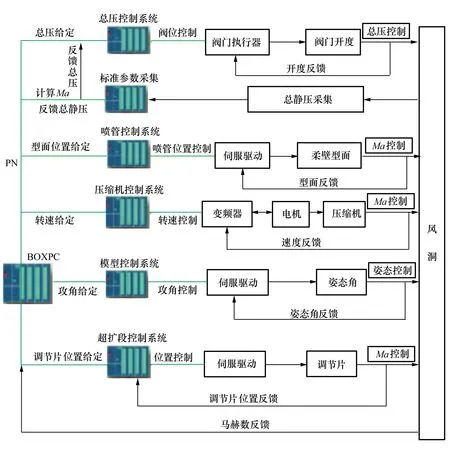
图1 流场参数控制原理

该风洞总压的调节手段及影响因素包括：抽真空泵转速、进气调节阀开度、排气/抽气调节阀开度、气源压力和洞体漏气量；静压没有直接的控制手段；马赫数的调节手段及影响因素包括：压缩机转速、喷管型面、超扩段型面、模型堵塞度等。

连续式风洞马赫数公式为

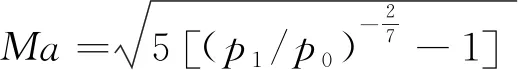
(1)

式中:p0为稳定段总压;p1为试验段静压。

由公式(1)可知,总压的调节直接影响马赫数,而实际中马赫数调节手段比如压缩机转速、半柔壁型面等在调节过程中又将导致总压的波动,这就导致马赫数与总压之间存在耦合,调节难度加大。总压和马赫数的耦合关系如图2所示。

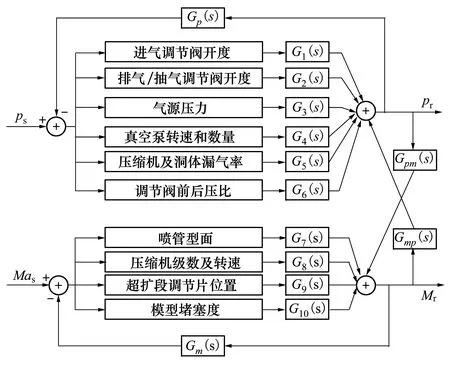
图2 总压、马赫数影响因素及耦合关系

但连续式超声速风洞和跨声速风洞的流场参数耦合特性又有所不同。一是马赫数精确调节方式不同,跨声速风洞需要通过对中心体/栅指型面、压缩机转速等调节手段实时闭环控制来实现马赫数精确调节,而超声速风洞主要通过喷管型面、超扩段型面精确调节到位后,利用压缩机转速来建立马赫数流场。另外,两者在马赫数和总压的耦合程度上也不同,超声速风洞的马赫数流场主要由压比决定,当压比一定时,总压波动对马赫数的影响较小;而跨声速风洞总压波动时马赫数波动较大。

由上述分析可知,对于工况复杂、状态多变的风洞总压与马赫数运行流场来说,由于流场参数调节手段多,相互耦合,很难获得精确数学模型,故而基于数学解耦的现代控制理论难于施行。因此在设计连续式跨声速风洞流场参数控制方法时,首先基于各自调节手段进行对应参数的闭环控制,同时结合马赫数与总压耦合关系,通过技术手段进行解耦来实现流场参数精确控制。

结合流场参数控制原理和耦合关系,拟通过高速网络设计来实现多调节手段的协调调度,通过高动态高精度的调节/测试手段和先进控制算法来保证流场参数的精确调节和快速稳定。

2 控制系统网路拓扑结构设计

测控系统以嵌入式控制器BoxPC 427E为核心,通过2套智能交换机组建光纤环网,实现风洞的流场控制,并负责对风洞运行相关子系统进行调度和协调控制。各子系统PLC之间采用Profinet RT通信,PLC控制器和伺服驱动器之间采用Profinet IRT进行通信,风洞整体控制调度(包括机构执行)周期控制在100 ms,满足流场参数控制系统对各调节手段的调度要求。

3 控制系统设计关键技术问题

流场参数的精确快速控制除先进的控制算法外还需要考虑时间特性(各机构的响应速度特性能否满足调度要求)、各执行机构/测试仪器的控制/测试精度能否满足流场参数控制精度指标、能否保证多变量逐次解耦的及时性,并确保能支撑起控制算法的高效性。

3.1 高精度采集系统设计

由于总压和马赫数控制精度要求较高,为保证控制的有效性，需要首先保证流场参数测试的准确性，压力采集精度对马赫数偏差的影响可用公式(2)来表示

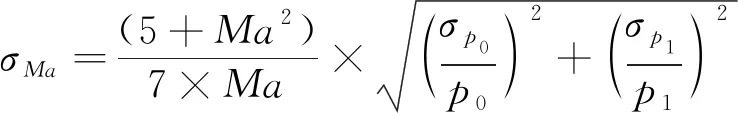
(2)

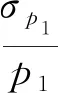
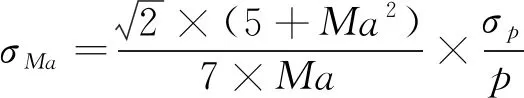
(3)

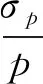
由公式(3)可知当目标马赫数越低，对压力采集的精度要求越高，而本风洞启动马赫数较高，避免了低马赫数下对测试仪器高精度的要求。同时，由(1)式得到静压随马赫数变化情况，如(4)式所示

(4)

由(4)式可得到不同稳定段总压下，马赫数阶梯变化时的静压变化，如图3所示。

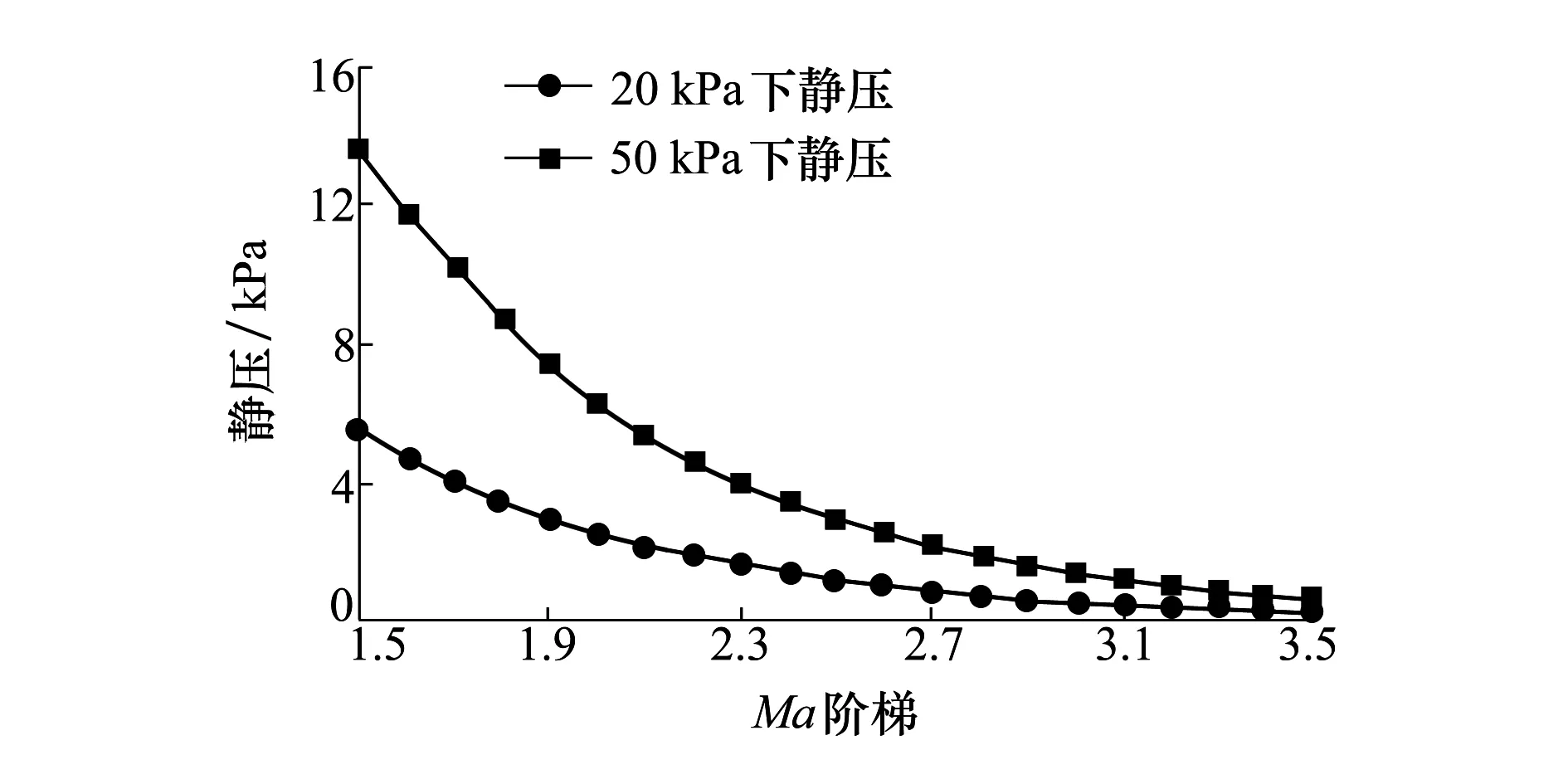
图3 不同总压下静压随马赫数变化情况

由图3可知，当马赫数达到3.0时静压只有几百帕，而若要保证总静压的精度，结合目前国内外压力传感器性能，选取0.02%精度压力传感器(其动态响应时间为20 ms)，并采用量程分段的方式以适应不同压力运行工况的测试需求。

3.2 伺服系统高精度及高动态响应特性设计

作为马赫数主要调节手段，半柔壁及超扩段等伺服系统需具备较高的定位精度和足够的动态响应特性,这里重点以柔壁为例来进行描述。半柔壁喷管由上下各6套伺服电动缸驱动，为保证气流均匀性和柔板不损坏，需要单侧6个轴同步运行，上下两侧各6个轴协调运行。柔壁控制系统以1516T-CPU作为控制器，配以Sinamic S120伺服驱动系统实现对半柔壁机构的多轴同步控制。T-CPU接受风洞核心控制器发送的型面控制命令，计算出各推杆运行目标位移，通过S120控制推杆的运动速度。机构上位移传感器实时采集各推杆的位移，反馈给T-CPU，与设定值不断比较，并对控制量进行修正，最终形成完整的位置闭环。伺服系统位置定位原理如图4所示。

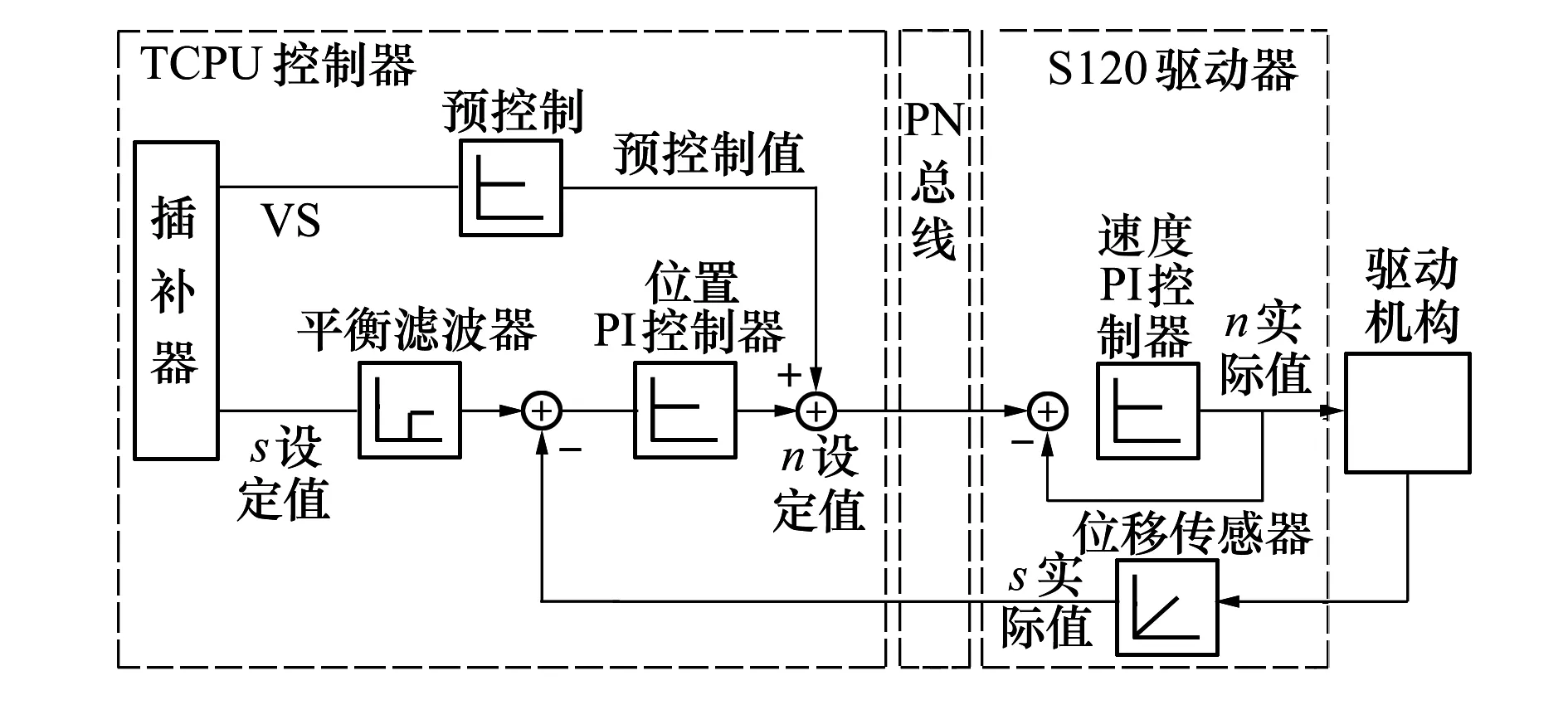
图4 伺服系统位置定位原理

伺服驱动机构的定位精度d(不考虑机构加工安装精度)由电机分辨率精度和位移传感器采集精度两部分组成，如(5)式(最大误差)所示

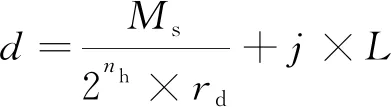
(5)

式中：Ms为推杆丝杠螺距；nh为电机单圈分辨率；rd为电机减速比；j为位移传感器满量程精度；L为位移传感器量程。

在确定机构定位精度要求后，据(5)式可反算各电机、位移传感器等精度参数。

为保证半柔壁单侧6个伺服轴运动过程同步运行，以1号轴为主轴，其他5个轴为从轴，每次运行前先计算各轴的齿轮比

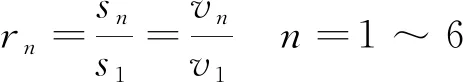
(6)

式中：rn为第n个轴的齿轮比；sn为第n个轴的当次行程；s1为主轴(1号轴)的当次行程；vn为第n个轴的匀速运行速度；v1为1号轴运行速度。

同时，为保证机构运动过程的平稳性，且同起同停，各轴之间应设置可变加速度，且加速度和各轴速度成正比，即

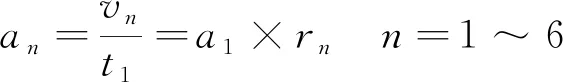
(7)

式中：an为第n个轴加速度；t1为1号轴加速时间，可结合控制器性能和调试需要设置该加速时间。

当前型面运行到位后，再走新的型面时，需重新计算各轴的目标行程，并计算齿轮比和加速度。

TCPU控制系统及伺服驱动系统采用PN-Drive通信协议，总线循环(控制)周期可缩短至3 ms以内。按照s=v×t，当控制周期足够短，控制器可识别出的各轴之间的不同步量越小，可及早重新对各轴进行位置调度，从而实现更精确的同步控制精度。

3.3 总压调节手段精度及动态响应特性设计

结合图2可知，总压调节手段主要包括调节阀开度、真空泵转速、气源压力等，而气源压力受外界影响，不容易控制。这样，总压的调节手段变成了真空泵转速和调节阀开度，而两者若同时调节，易出现相互耦合。因此，压力闭环时，真空泵转速采用前馈控制(不同目标压力阶梯下预置调节)，而利用调节阀进行精调。忽略风洞漏气，连续式风洞总压控制精度可参考(8)式[16]：

式中：p为压力波动量；ps为目标压力；QVmax为阀门最大体积流量;M为空气摩尔质量；R1为气体状态常数；调节时间为t；x为阀门开度比；R为阀门的可调比；阀门调节过程平均速度为vs；阀门可识别的位置精度(分辨率)为d；s为阀阻比。

考虑到洞体容积较小，只有50 m3，而一般调节阀R=50，同时排气和抽真空调节阀共用，流量较大(10 min内常压抽至20 kPa)，结合(8)式，并基于现有市面上调节阀的性能，要求调节阀定位精度优于0.2%，速度(时间)优于25～30 s。

3.4 压缩机转速控制精度及动态响应特性设计

压缩机系统作为动力源，是连续式超声速风洞最重要的系统，而且压缩机系统能耗很大，这就对压缩机的动态特性有很高要求。同时，稳定段总压和风速的关系如(9)式所示

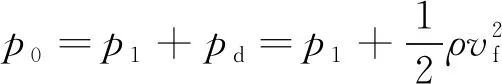
(9)

式中:p0为总压；p1为静压；pd为动压；ρ为密度；vf为风速。作为马赫数主要调节手段之一，当压缩机转速波动时，(9)式中的静压、密度等均会发生变化，进而导致总压波动。

结合其他连续式跨声速风洞设计要求(比如0.6 m风洞)和现有压缩机设计水平，要求压缩机转速控制精度达到0.03%，最大升降速度为90 s以内。

4 分段变参数加模糊PI算法实现总压控制

由于连续式超声速风洞马赫数无需主控系统精确调节，在解耦控制时主要考虑马赫数调节手段对总压的影响。而在风洞流场参数控制领域，使用较多的算法包括PID控制、模糊控制和预测控制等，考虑到超声速风洞要建立准确的数学模型很困难，以分段模糊PI控制算法为核心来实施总压控制。总压控制策略为：增压时采用进气调节阀预置，排气调节阀精调，负压时采用进气调节阀预置，抽气调节阀加真空泵精调的总压控制方式。设计时先采用前馈控制方式实施压力粗调，待压力进入调节阈值q(t)(设定为目标压力的96%～104%)后再采用分段变参数加模糊PI控制算法进行总压精确控制，即在模糊PI的基础上，首先根据目标总压调试获取不同目标压力下的分段的PI控制参数作为模糊PI基准参数，尔后由模糊算法结合压力目标和调节阀特性进行变参数控制。其原理框图如图5所示。

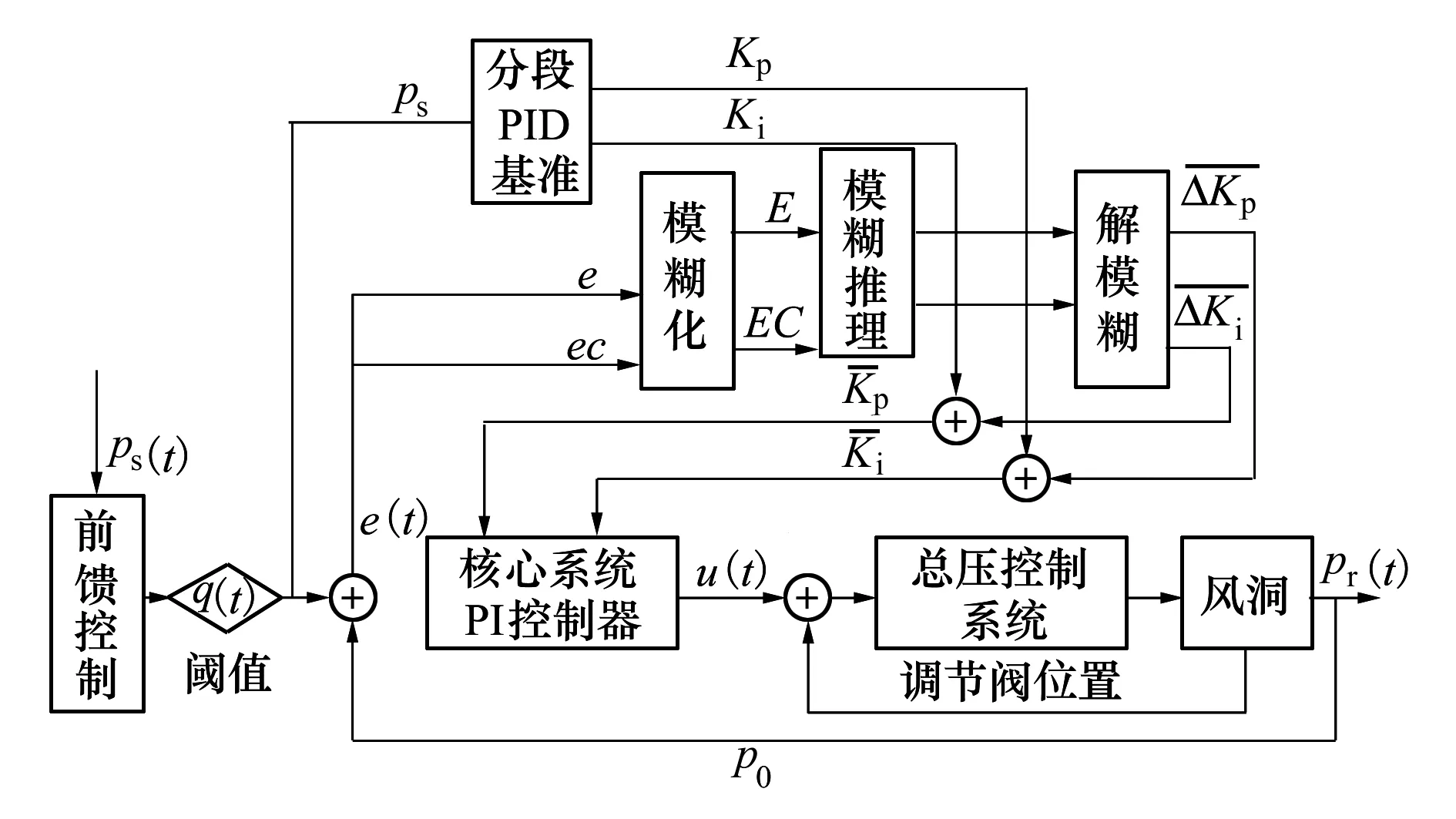
图5 总压控制算法调节原理

模糊PI以PI控制器为基础，PI控制器根据压力的给定值s(t)和实际值r(t)的偏差e(t)与比例系数Kp、积分时间Ti组合构成控制量输出，对被控对象进行控制，其控制规律为

(10)

离散化处理后得到(11)式

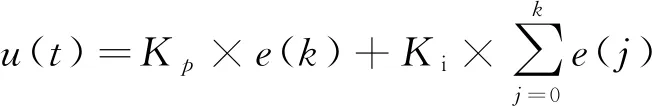
(11)

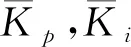
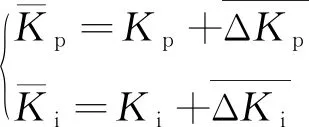
(12)

模糊PI的控制算法描述相对较多，这里就不过多叙述[17-19]。

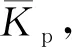
考虑到压缩机密封气系统往风洞内漏密封气(固有特性)，风洞增压及低真空工况下，需要通过开启进气阀进行流量补偿，以确保排气/抽气调节阀处于合理的调节区间。进入调节阈值q(t)后，进气调节阀开度V(x)与气源压力pa、目标总压ps满足(12)式

(13)

同时，负压工况下真空泵转速np也随着(13)式进行预置调节，以防止低真空下抽气系统流量过大，导致抽气调节阀进入调节死区。

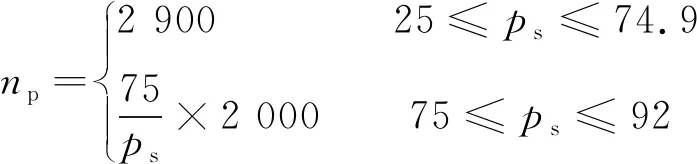
(14)

5 运行控制流程设计及试验结果

连续式超声速风洞能耗大，合理优化的运行控制流程是试验效率优化的前提保证，风洞运行控制主要流程如图6所示。考虑到马赫数和总压的耦合，在启动或变马赫数阶梯时先利用马赫数调节手段进行预置，待马赫数相对稳定后，再利用总压控制算法实施压力闭环调节。

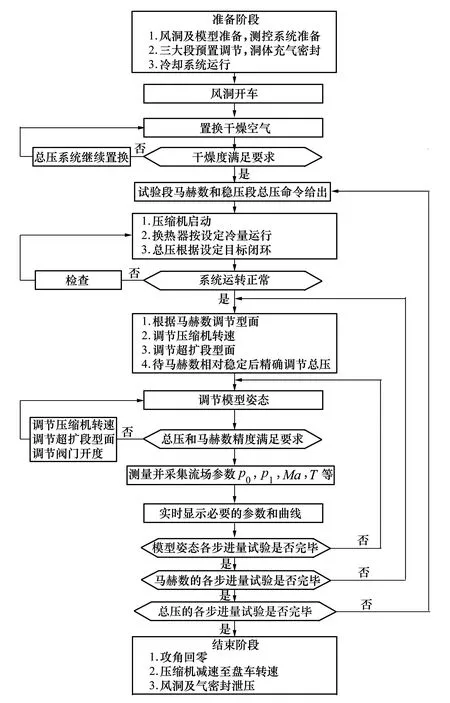
图6 风洞运行控制流程图

风洞于2020年开始建设，2021年建设完毕，经过测试，柔壁和超扩段、模型支撑系统机构定位精度优于0.01 mm，同步过程中各轴的不同步量小于0.05 mm。压缩机转速控制精度约0.03%。总压系统调节阀调整为气驱调节阀，实际定位精度仅为0.5%(分辨率0.5%)，速度为3.2%/s(每秒3.2%的全行程)；受气驱调节阀死区及动态响应时间影响，调节阀可用调节开度范围为2%～98%。

风洞吹风结果以2021060201和2021060301 2个典型车次进行描述，试验条件为变总压、变马赫数。马赫数调节方式为固定压缩机转速调节，攻角固定为0°(该风洞目前仅安装移测架)，流场稳定后采用总压探针移测架进行移测测试。图7和图8分别为20 kPa和60 kPa下变马赫数测试结果(车次为2021060301)，图9为100 kPa下变马赫数测试结果(车次为2021060201)。在喷管运动过程中型面号保持为前一值，只有型面完全成型时，当前型面号才会更新。

从图7～9中可知，趋稳后压力控制精度优于0.05%(图中总压虚线范围)，试验段马赫数单点稳态控制精度可优于0.000 3(图中马赫数虚线范围)。

由图7～9中可知，当压缩机转速一定时，柔壁型面扩开，马赫数增大，总压增大；型面收缩，马赫数减小，总压跟随下降。当压比达到对应的马赫数时，马赫数主要受型面影响，与转速关系不大。总压变阶梯调节或者当缓慢改变型面或压缩机转速时，总压稳定较快，超调较小；当快速调节型面或大幅调整转速时会带来总压较大幅度的变化(总压会很快超出精度范围，如图中的各尖峰)。

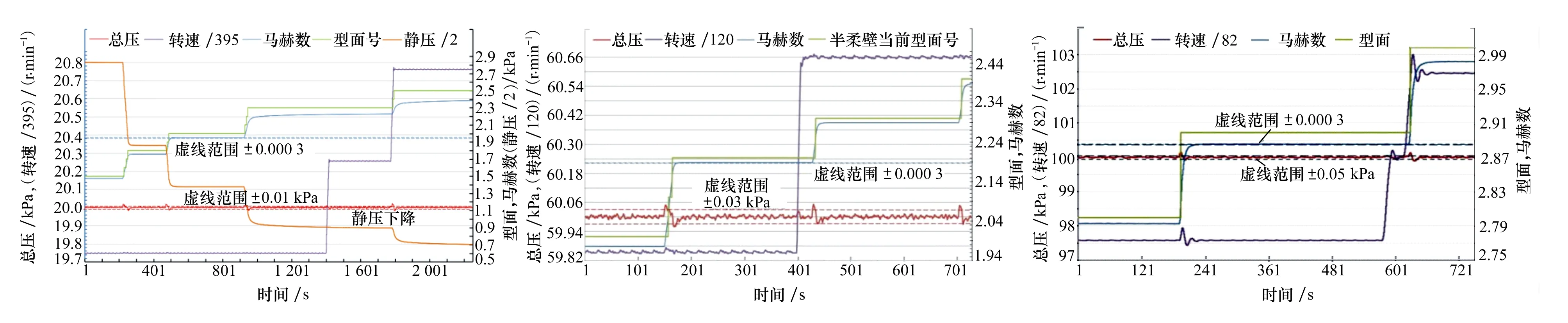
图7 20 kPa下流场参数测试结果 图8 60 kPa下流场参数测试结果 图9 100 kPa时流场参数测试结果

调节马赫数时(转速不变)，总压和马赫数的稳定时间与马赫数调节阶梯幅度大小、柔壁型面行走时间等相关，平均来看，相邻2个马赫数之间总压稳定时间约20～30 s，马赫数稳定时间约25～35 s。

部分工况下试验段马赫数稳定较慢(如图7所示高马赫数)，主要原因是当总压到达控制精度后，静压仍缓慢下降，导致马赫数稳定存在滞后现象，该现象有可能由以下原因造成，一是该工况下静压很低(有时甚至低于1 kPa)，而静压传感器绝对精度仅为12 Pa，测试精度存在一定偏差；二是在对应工况下，试验段入口侧壁处可能存在持续膨胀加速过程，怀疑与风洞压比建立情况(负压下压缩机性能变化)或者负压下喷管内部流场变动有关。上述现象还有待进一步分析研究。

另外总压理论上调节精度可以更高，因为风洞用于精调的排/抽调节阀定位精度及分辨率离设计指标有较大差距。

6 结 论

经过试验验证可以得出以下结论：

1) 利用本文提出的连续式风洞控制系统设计方法，能够实现流场指标的精确控制，其中总压稳态控制精度可达0.05%(设计指标增压/增压0.1%，负压0.2%)，试验段马赫数稳态精度优于0.000 3，均达到国军标先进水平。

2) 本文可为其他连续式超声速风洞以及大型连续式超声速风洞的设计调试奠定基础。

下一步将重点优化试验效率，包括优化风洞运行流程、优化控制算法并进一步提高流场参数稳定时间，并针对部分工况下马赫数稳定较慢的问题进行深入研究。