低轨巨型链形星座解析设计及效能分析

郑鹏飞, 陈宏宇, 郭崇滨

(1.中国科学院微小卫星创新研究院, 上海 201203; 2.中国科学院大学, 北京 100049;3.上海微小卫星工程中心, 上海 201203)

目前,低轨巨型星座发展迅速,如中国航天科技集团“鸿雁”星座(360余颗)、中国航天科工集团“虹云”星座(156颗)、美国SpaceX公司“Starlink”星座(4.2万颗)等。该类星座一般采用大量的低轨微小卫星组网实现近实时覆盖,经典的Walker-δ、共地面轨迹等星座卫星分布均匀性较差且难以利用解析法快速设计。

应用于低重访时间覆盖的经典星座类型主要有2种:①典型的Walker星座[1],包括星形构型、δ构型、σ构型、玫瑰构型等;Peng等[2]提出了Brush Line构型星座,采用多星沿经度扫描的思想实现全球覆盖,但其连续覆盖性较差;He等[3]针对通信定位问题,综合考虑轨道高度、倾角等参数设计了多倾角组合的低轨δ星座实现连续覆盖,但复合星座构型不稳定且维持较复杂，难以建立星间链路。②共地面轨迹(repeat ground track,RGT)星座,该星座所有卫星的地面轨迹重复,但每个轨道面上仅有一颗卫星;Lee[4]针对特定目标的连续覆盖对比分析了RGT星座和δ星座的数量差异,在重访时间要求较大(20 min以上)时,RGT星座规模显著小于δ星座,在重访时间要求较小(10 min以内)时二者差别不大;SpaceX公司的专利[5]显示Starlink的Ⅲ期星座(7 518颗)欲采用多个共地面轨迹的星簇组成。

针对以上星座的常规设计方法主要有2种:①利用解析法设计星座参考码并进行数值仿真、人工选优,一般能够快速得到满足任务需求的星座;王茂才等[6]根据任务需求人工选取几组参数,仿真选优设计了双层对地观测星座;Ulybyshev利用解析法分析覆盖性[7],设计了近极轨和赤道圆轨道弱对称的非均匀卫星星座。②利用优化算法搜索轨道的最优解或星座参考码的最优解;马剑、Lake、贺波勇、沈欣等[8-11]用遗传算法、多目标进化算法、改进粒子群优化算法等设计了不同任务需求的星座,该方法存在算法求解时间较长、算法复杂、优化目标单一等问题。

Walker[1]提出了覆盖性和经济性均较好的Walker-σ星座,该星座的星下点轨迹重合且形成一条类似正弦曲线的不自相交封闭曲线,覆盖特性均匀,但该构型依赖于回归轨道,维持该轨道所消耗的燃料较大,不利于低轨星座的长期维护。因此,参考σ星座的设计思想,本文提出了一种低轨链形星座,并基于覆盖要求和传感器视场角推导了解析设计方案,以对地侦察任务为例设计了一个包含132颗卫星的链形星座,从覆盖性和星间链路角度与常规δ星座和RGT星座对比分析,验证了链形星座效能。

1 低轨巨型链形星座及解析设计法

1.1 链形星座描述

Walker-σ星座轨道一般选取中、高回归地球轨道,从而实现所有卫星的星下点轨迹重合,而低轨非回归轨道Walker星座无法实现。借鉴σ星座封闭曲线覆盖特性的思想,设计合理的相位参数,使得低轨Walker星座的星间链路连线在二维地图的投影类似于一条或多条自封闭的正弦曲线,卫星在该曲线上等时间间隔分布,该链状构型随时间动态移动实现对所有经度范围的覆盖,称之为Walker-链形星座,如图1所示。

图1 链形星座示意图

为描述链形星座构型,参考σ星座描述方法[12],引入相位配置参数M(M为正整数)、卫星数量N,星座中所有卫星的轨道倾角均为i,轨道平均高度均为h,偏心率均为e,近地点幅角均为ω,升交点赤经为Ω,相位角为u,则顺序相随的2颗卫星之间的升交点赤经差和相位差为

(1)

通过选取不同的N和M的值,可得到不同覆盖性能的链形星座。

1.2 解析设计理论推导

1.2.1 轨道设计

1) 轨道高度

低地球轨道卫星一般处于Van-Allen内带以下避免高强度辐射,同时过低的轨道受到的大气阻力较大,因此可根据传感器探测距离选择平均高度为300～1 500 km内的轨道。

2) 轨道倾角

Walker星座一般应用于纬度带覆盖,倾角的选择取决于纬度带的覆盖要求和传感器的视场角,在覆盖要求为南北纬θN,S角度之间时,设传感器的半视场角为α,对应的地心角为β,如图2所示。

图2 单星地面覆盖性示意图

由几何关系可得

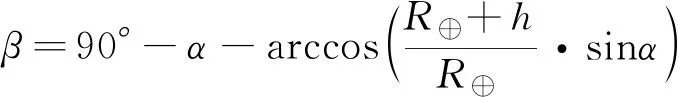
(2)

式中,地球平均半径R⨁=6 378.137 km。

则轨道倾角值的选取可参考

i=θN,S-β+ζ

(3)

式中,ζ的一般取值为1°～3°，以完全覆盖纬度带的边缘部分。

3) 轨道偏心率和近地点幅角

通常低地球轨道选取圆轨道,此时偏心率e=0,近地点幅角此时无意义,令ω=0°。

1.2.2 升交点赤经和相位设计

在链形星座的相位配置中,为实现对纬度带的低重访覆盖,需使链路中顺序相随的卫星覆盖范围、链与链之间的卫星覆盖范围在空间上邻接。

令任意顺序相随的2颗卫星邻接,可使整个链形星座顺序邻接,顺序相随的2颗卫星距离远近决定了重访时间的大小。在地心第三赤道坐标系(卫星Sat1位于升交点时)中表示出顺序相随的2颗卫星位置:以赤道面为XOY面,原点O为地心,X轴指向卫星Sat1的升交点,Z轴指向北极。

由图3可以得到卫星Sat1和卫星Sat2的坐标(φ为赤经,λ为赤纬)为

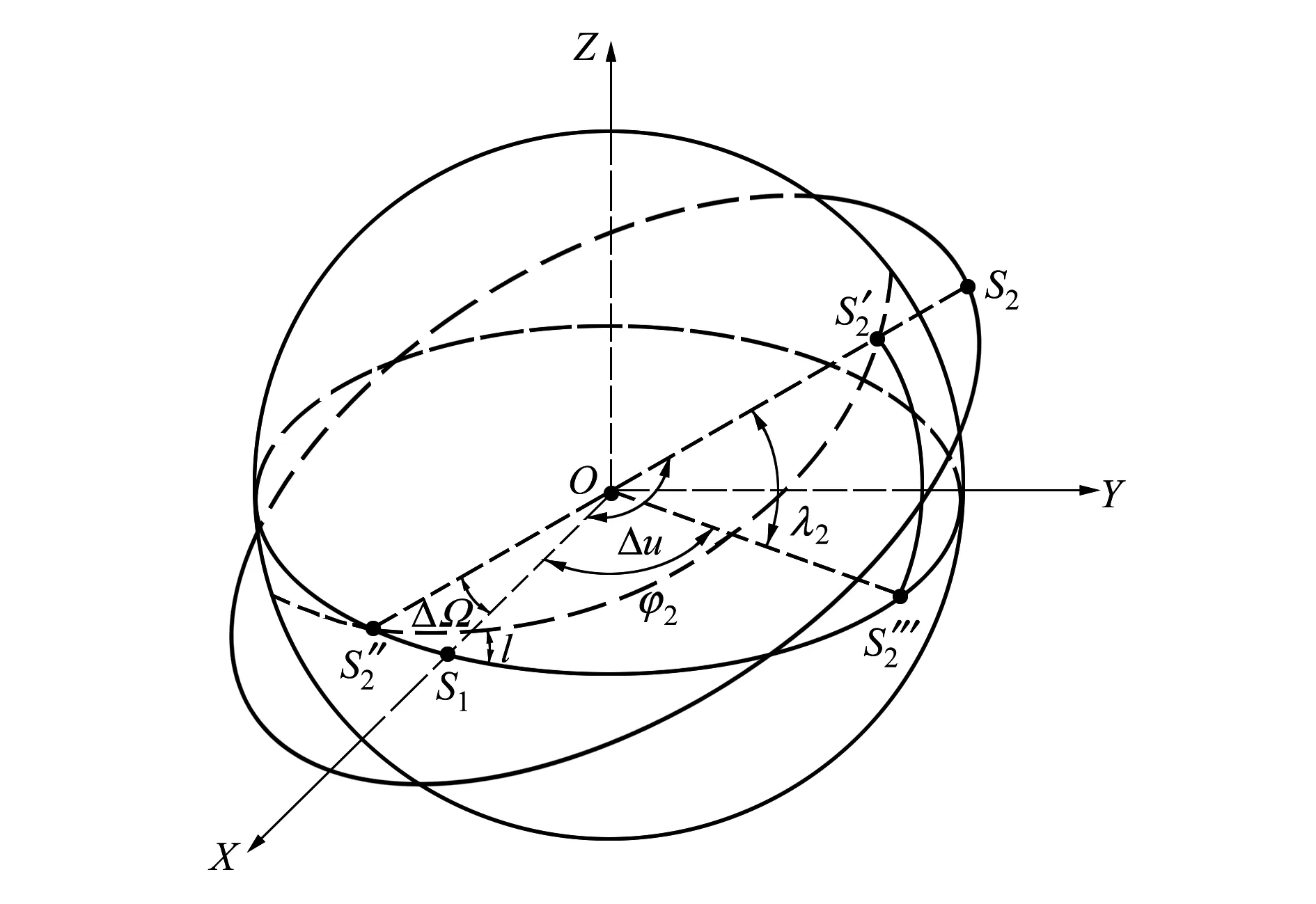
图3 地心第三赤道坐标系下的卫星示意图

(4)

表1 图3中的主要符号及其含义

将顺序相随的卫星链路连线可形成一条闭合的曲线,随着M取值的不同,链路的起伏程度不同,对地面的均匀覆盖性也不同,用赤经差和赤纬差的比率γ来描述链路的起伏程度

(5)

由图4可知,γ越大,则链路的瞬时覆盖间隙越大,重访时间越高;γ越小,则链路起伏越陡峭,瞬时覆盖均匀性越好,重访时间越小。

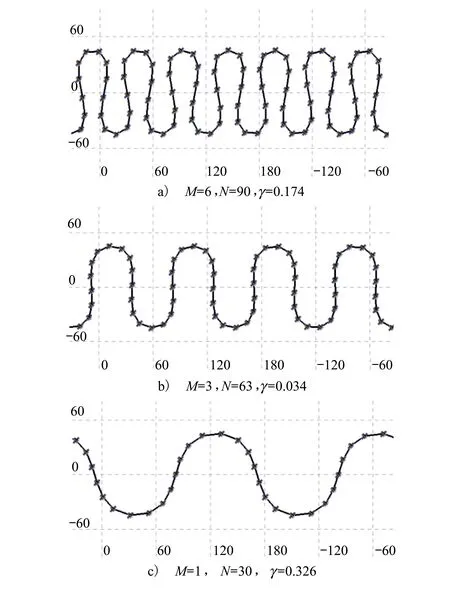
图4 M取不同值时链形星座起伏程度示意图

为保证顺序相随的卫星覆盖范围邻接,要求顺序相随的卫星赤纬差符合(6)式要求

Δλ=|λ2-λ1|=2β·ε

(6)

ε定义为连续覆盖控制因子,ε越小,则星座的连续覆盖性越好,重访时间越小,但所需的卫星数量N增加。

由(4)式和(6)式可得Δu的取值范围

(7)

结合(4)式和(5)式可得M值的选取依据为

(8)

(8)式为超越方程,无法直接求解,可绘制γ关于M和Δu的图像,根据图像选取γ取最小值时对应的M值,然后根据Δu的范围结合(1)式得到N值的范围,从而得到一组或多组链形星座参考码。

1.2.3 单链形星座与多链形星座的转换

链形星座是一种特殊的δ星座,可用δ星座参考码表示。包含单条链路的链形星座瞬时覆盖范围可能无法覆盖所有经度,可将多个链形星座组合实现纬度带的瞬时全覆盖,此时仍然为一个特殊的δ星座,因此利用δ星座参考码进行转换。

1) 单链形星座参考码转换为δ星座参考码

δ星座参考码为N/P/F,N为卫星数量,P为轨道面数量,F为相位因子,单链形星座与δ星座的参考码对应为[12]

(9)

(9)式中相位因子F是[0,P-1]内的整数,由此整数系数K可唯一确定。

2) 多链形星座参考码转换为δ星座参考码

单链形星座对应的δ星座参考码为N1/P1/F1,则包含n条链(n为奇数)的多链形星座对应的δ星座参考码N2/P2/F2为

(10)

式中,当n为偶数时,多个单链形星座在空间上重叠,无法增加瞬时覆盖率,因此n仅能取奇数,此时多条链形在空间上错开,瞬时覆盖率增加。

相比于单链形星座,多链形星座每个轨道面上的卫星数量扩大n倍,但轨道面数量不变,有利于一箭多星技术的利用,极大地降低发射成本。

1.2.4 设计流程

综上所述可得链形星座设计流程为:

step1 确定传感器视场角和覆盖纬度需求,选取合适的轨道;

step2 根据重访时间的需求选取ε取值范围,利用图解法得到一组或多组链形星座参考码;

step3 根据瞬时覆盖率选取是否转换为多链形星座,并从多组结果中仿真选优,一般选取卫星数量最少的方案作为设计结果。

2 低轨对地侦察链形星座设计

空间对地侦察星座具有覆盖范围广、探测距离远、隐蔽性强等优点,已成为重要的情报来源。第16任北约盟军最高司令斯塔夫里迪斯上将[13]阐述了未来几十年美军在太平洋对华作战的设想,美军的总体海上战略态势是建立全球海上联盟,并有针对性地增强美方在西太平洋的前沿存在和作战能力;彭耿等[14]针对卫星侦察时效需求建立了侦察卫星支援反舰导弹作战的基本模型,计算结果表明当卫星侦察定位精度为4 km时,目指信息要求的最大时延约为4～6 min;郭福成等[15]在分析侦察卫星瞬时覆盖范围时提到对于高度在500～1 000 km的卫星,其侦察范围可达2 500～3 000 km;高世杰等[16]提到对于大规模星座,需具备星间链路以降低地面测控压力并提高数据实时回传能力。

综上所述,可得到侦察任务的需求为:

1) 面向全球热点地区和海洋地区,即在南纬60°和北纬60°之间实现低重访时间覆盖;

2) 对南北纬60°之间的任意地点平均重访时间在4 min以内、最大重访时间在6 min以内;

3) 星载传感器的半视场角为50°,可简化为对地圆锥视场,探测距离小于1 500 km;

4) 星座需在当前星间激光通信载荷能力下建立永久性星间链路;

根据任务需求,设计低轨链形星座,并按照经典方法设计常规δ星座和RGT星座，对比分析效能。

2.1 链形星座设计

2.1.1 轨道设计

传感器视场角固定时,探测距离小于1 500 km范围内,轨道高度越高,瞬时覆盖范围越大,设计轨道高度为800 km,偏心率为0。

结合(2)式和(3)式可得轨道倾角为

(11)

将数值代入(11)式可得轨道倾角为50.44°,令i=53°以完全覆盖纬度带的边缘部分。

2.1.2 升交点赤经和相位设计

由(8)式可知γ的取值主要取决于M,因此连续覆盖控制因子ε可选取较大的范围:[0.8,1.2],进而由(7)式可得Δu的范围为[19.62°,29.73°]。在Δu的取值范围内,根据(8)式绘制γ关于M和Δu的图像如图5所示。

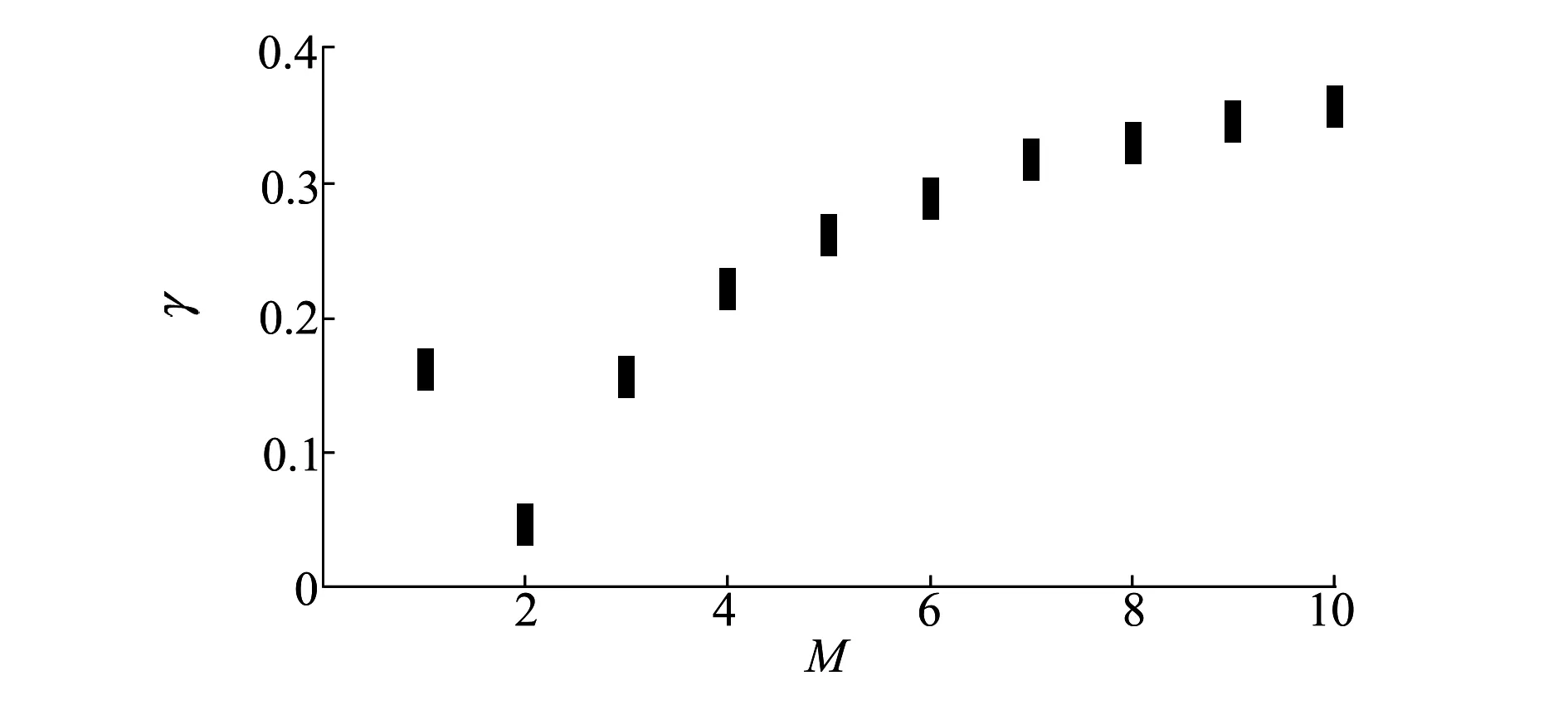
图5 链路起伏程度γ在Δu范围内关于M的图像

由图5可知,γ取最小时对应M值为2,则根据(1)式可得N的取值范围为(37,55)之间的偶数,可得如图6所示的单链形星座。

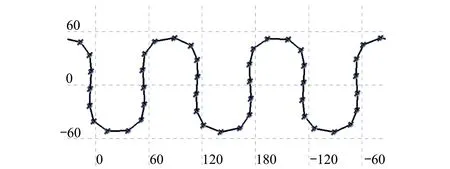
图6 单链形星座设计结果M=2

从图6可以看出,单链无法满足纬度带的瞬时覆盖,需设计多链形星座,根据(9)式和(10)式将单链形星座转换为多链形星座,得到初步设计结果。

依据表2由卫星数量最少的方案开始在STK(美国Analytical Graphics公司卫星工具包)中仿真计算重访时间,直至符合任务需求,可得M=2,N=44对应δ星座参考码为132/22/13的多链形星座符合要求,根据(1)式可得星座的升交点赤经差和相位差为

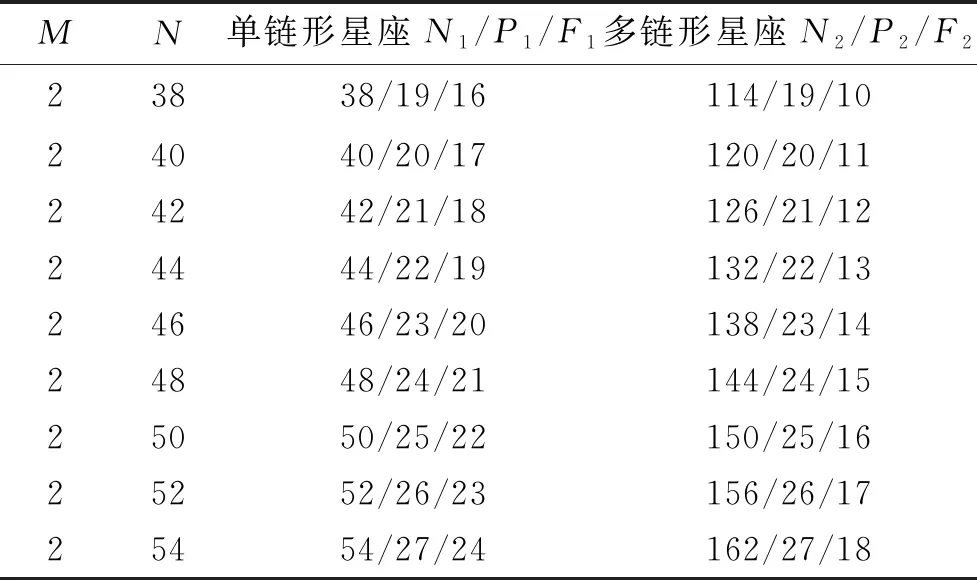
表2 链形星座初步设计结果

(12)

星座在二维地图上的投影如图7所示:

图7 多链形星座设计结果(132颗)

2.2 对比星座设计

2.2.1 Walker-δ星座常规设计

δ星座的参考码为N/P/F,P为轨道面数量,F为相位因子,确定δ星座升交点赤经差和同轨道面相位差的方程为[12]

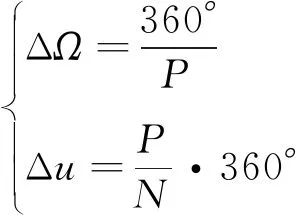
(13)

设计δ星座轨道与链形星座相同,采用遗传算法设计得到的δ星座结果与链形星座完全相同,但算法复杂、优化计算时间超过2天;采用经验法设计时[12],相位因子通常取0或1,通过枚举法仿真不同卫星数量的常规δ星座,结果如图8所示。

图8 平均/最大重访时间随卫星数量变化图

由图8综合权衡可得参考码为170/17/0的常规δ星座基本满足任务需求且数量最优,如图9所示。

图9 常规δ星座设计结果(170颗)

2.2.2 共地面轨迹星座设计

共地面轨迹星座中所有卫星具有相同的地面轨迹,顺序相随的卫星升交点赤经差和相位差需满足[17]

(14)

式中:ω⨁=7.292 115×10-5rad/s为地球平均自转角速度;ωs为卫星的在轨角速度,由轨道高度h决定。

根据(14)式,按照卫星数量由少至多顺序,即相位差Δu值由大至小枚举仿真,可得满足任务要求的共地面轨迹星座卫星数量N=160,每个轨道面仅有1颗卫星,相位差Δu=32.11°,如图10所示。

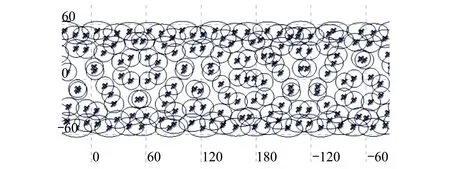
图10 RGT星座设计结果(160颗)

3 效能分析

星座效能主要体现为经济性、覆盖性和星间链路特性,在均满足对地侦察任务需求的条件下,对比分析3种星座效能。

由表3可知,链形星座所需的卫星数量最少,仅为132颗,而常规δ星座数量是其1.3倍，RGT星座数量是其1.2倍;链形星座和常规δ星座每个轨道面均包含多颗卫星,可利用一箭多星技术降低发射成本,而RGT星座每个轨道面仅有1颗卫星,星座部署成本大大增加。

表3 对地侦察星座设计结果

3.1 覆盖性分析

针对纬度带的低重访覆盖,主要的覆盖性指标有重访时间和覆盖时间比,设置仿真时长为一天,通过STK仿真得到3种星座的覆盖时间比、重访时间随纬度变化如图11～12所示。

由图11可知,链形星座覆盖时间比在73%以上,而常规δ星座为63%以上，RGT星座仅为56%以上。

图11 3种星座覆盖时间比对比图

由图12可知,除RGT星座的重复地面轨迹特性使其在极少数地区重访时间过大,3种星座均满足最大重访时间小于6 min、平均重访时间小于4 min,链形星座的平均重访时间在2 min以内,且在不同纬度上较均匀,而常规δ星座和RGT星座在赤道地区的覆盖性起伏较大、劣于中高纬度地区。

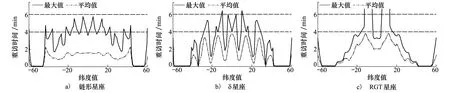
图12 3种星座平均和最大重访时间对比图

重访时间越小、覆盖时间比越大则对地侦察时间越长,因此链形星座的覆盖性能优于常规δ星座和RGT星座。

3.2 星间链路分析

卫星可以与前后左右4颗卫星建立星间链路,携带多个激光通信载荷分别对准不同的卫星,因此,通过卫星姿态机动仅能实现2颗卫星的对准,无法同时完成所有激光链路的持续对准,这就要求激光通信载荷自身需具备一定的转动能力[16]。通信距离、转向能力是限制建立星间激光链路的主要指标,如德国Mynaric公司[18]研制的星载激光通信终端通信距离小于4 500 km,方向角转动范围为±175°,俯仰角转动范围为+5°～-25°。激光通信终端的俯仰改变靠自身转动实现,大范围的方向角改变需依赖卫星的偏航姿态机动,而星载传感器为对地指向,偏航机动对星座覆盖性能无影响。

依据可见性约束设计永久性链路。

1) 链形星座星间链路设计

链形星座的分布特性使其可以按照顺序相随的卫星建立1条闭合的星间链路;则3条链可分别建立3条闭合的星间链路。另外可在链与链之间建立链路,共可建4条闭合链路;则链形星座的全连通星间链路如图15所示。

图13 链形星座同链星间链路(1条) 图14 链形星座异链星间链路(1条) 图15 链形星座星间链路设计结果

2) 常规δ星座星间链路设计

针对170/17/0的常规δ星座,其不同轨道面对应序号的卫星始终处在同一赤纬上,因此不同轨道面上同序号的卫星共计可组成10条异轨道面星间链路;该星座同轨道面上的卫星共计可组成17条闭合的同轨道面星间链路;则常规δ星座的全连通星间链路如图18所示。

图16 常规δ星座异轨道面星间链路(10条) 图17 常规δ星座同轨道面星间链路(17条) 图18 常规δ星座星间链路设计结果

3) RGT星座星间链路设计

RGT星座具有重复地面轨迹的特性,因此可将RGT星座的所有卫星按轨道面顺序相连,得到1条完整的星间链路;同时,RGT星座可按照间隔地面轨迹的顺序形成1条闭合的星间链路;则RGT星座的全连通星间链路如图21所示。

图19 RGT星座同轨迹链路(1条) 图20 RGT星座异轨迹链路(1条) 图21 RGT星座星间链路设计结果

4) 对比分析

对以上3种星座建立的6种链路进行分析,结果如表4所示。由表可知,3种星座均能建立全连通的永久性星间链路,链路指标均在正常范围内,链形星座的同链星间链路观测方位角、俯仰角、角速率的变化范围均较小,能够较容易地建立3条完整的链路实现全部连接,而常规δ星座至少需要10条异轨道链路,RGT星座的链路距离较大,且仅为1条闭合链路、稳健性不高;链形星座的异链星间链路的距离较大,可作为同链链路的补充,实现星座全连通。

表4 3种星座星间链路对比

4 结 论

本文面向低重访时间覆盖需求提供了一种低轨巨型链形星座及解析设计方法,该方法依据覆盖要求和传感器视场角,在超越方程的多组解中仿真选优,能快速设计出符合重访时间需求的低轨巨型星座。以对地侦察任务为例设计了一个132颗卫星的低轨链形星座,相较于常规δ星座、RGT星座所需卫星数量更少、覆盖更均匀、重访时间更小、容易建立永久性星间链路。未来可针对重访时间要求θN,S与链形星座相位差Δu、相位配置参数M的关系作进一步研究,以缩小连续覆盖控制因子ε的取值范围,从而减小超越方程解的数量。