面向小样本数据的水下目标识别神经网络深层化研究

吴晏辰, 王英民

(西北工业大学 航海学院, 陕西 西安 710072)

水下目标识别作为水声工程的重要技术领域,一直是海洋军事和民用的主要研究方向之一。随着近年来水下军事目标小型化、消声化,民用目标复杂化、精确化的趋势不断加深,对于水下目标识别系统的精度和灵敏度都产生了更高的要求[1]。

与传统的利用基于先验知识的人工听音和谱图等信息进行目标识别不同,利用基于深度学习的水下目标识别系统,可以满足现代海洋作战、作业对于目标自动识别、快速识别的迫切需求[2]。能够实现这一需求的主要原因在于深度学习提取目标声学信号中的各类特征作为基础,利用信号处理的方法,将多种信号特征通过近年来蓬勃发展的各类人工智能分类器,以实现自动识别的目的。现有研究表明,目前利用各种方法所提取的信号特征在用于水下目标识别时,在实验室验证的效果普遍较好,但在实际水下噪声环境中,应用性能却出现了明显下降[3]。出现这种现象的主要原因在于:一是相较于实验环境,实际水下环境复杂许多,相应的样本数量与基于大数据的深度学习网络所需的量较少;二是在复杂声环境下的信号信噪比不佳,存在多目标或强干扰的情况下,容易导致特征提取出现误差偏离;三是对于目标声信号本质的特征提取方法的研究还不够。

为了研究产生应用性差异的原因,本文选择了2种具有相关性且有较为明显差异的特征提取方法。作为目标应用最广泛的水声特征提取方法,梅尔倒谱系数特征提取方法(Mel-frequency cepstral coefficients,MFCC)可以将声音信号的实际频谱转化到感知频域中进行研究,从而有利于系统模拟人的感知过程,在性能和稳健性方面比较符合实际的听觉效果[4]。而在MFCC基础上改进的Gammatone频率倒谱系数法(Gammatone frequency cepstrum coefficient,GFCC)在保有MFCC优点的同时,在水下复杂声场环境中, GFCC较MFCC具有更优良的抗噪能力[5]。

2006年Hinton提出了以卷积神经网络(convolutional neural network,CNN)为主体的深度学习模型[6]。CNN具有自适应寻找最适合分类器的能力,CNN由于采样层的存在,具有时移不变性的特征[7]。与传统识别方法相比,CNN通过寻找使识别效果最优的参数,使网络可以摆脱人工经验的影响,对复杂的应用条件具有更好的适应能力。而基于CNN卷积核改进的残差神经网络(ResNet),充分利用了神经网络的函数拟合特性,对于水下目标的辐射信号而言,基于CNN的深度残差网络可以一定程度上获取常规特征分析方法难以发现的隐含关联,即作为特征提取器的同时,亦可作为分类器,因此非常适合处理原始水声信号。

本文给出了一个面对水下目标识别小样本数据的基于卷积神经网络的深层神经网络构成方法。利用MFCC和基于MFCC改进的GFCC作为特征提取方法,构建卷积神经网络与残差神经网络形成比对网络,建立了小样本下的水下目标识别系统,并对样本在2种网络的较深层结构下所取得的实际识别率与网络预测值进行统计比对。发现由于特征提取方法与深度学习网络的各种组合模式对于水声信号诸如信噪比等特性的匹配程度不同,其表现出的实际识别率和网络预测值有较为明显的关系,抗噪较好的组合模式的梯度衰减、网络识别稳定性和实际识别率较抗噪较差的组合具有更佳的网络稳定性和准确率,根据这一依据,为复杂神经网络神经元的设计提供了一种思路。

1 舰船辐射噪声的特征提取

1.1 MFCC特征提取法

作为一种常见的声音识别特征,MFCC特征提取方法主要分以下几步:

1) 分帧

2) 求能量谱

为了得到信号能量谱,需要利用快速傅里叶变换对帧信号进行处理,其公式为

p(f)=|X(f)2|=|FFT(x(n))|2

(1)

式中,x(n)为输入信号。

3) 滤波

将p(f)通过梅尔滤波器组,其公式为

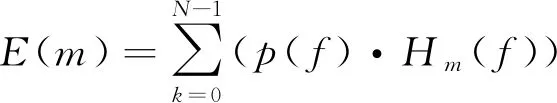
(2)

式中:N为帧数；Hm(f)为梅尔滤波器组系数。

4) 对数运算

对(2)式中E(m)求导,得到E′(m)

5) 求倒谱

对E′(m)求离散余弦变换,可得MFCC参数C(n),其公式为

(3)

式中:n=1,2,…,p,p为MFCC的阶数；M为滤波器的个数。

则MFCC特征参数的一阶以及二阶差分系数由(3)式可得,其公式分别为

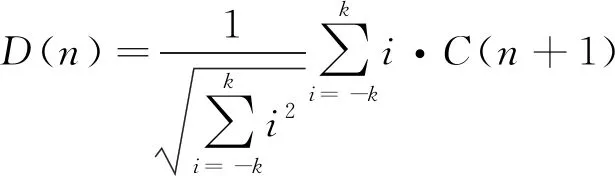
(4)

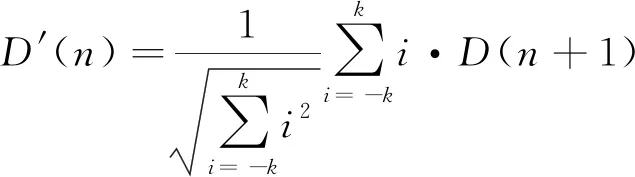
(5)

(3)～(5)式共同构成帧特征向量

Tn={C(n),D(n),D′(n)}

(6)

(6)式即为样本信号的MFCC。

为了使系统的性能以及稳健性都相对符合人听觉感知效果,利用MFCC特征参数分析方法将声音信号频谱转换到模拟听觉感知过程的感知频域。图1为梅尔频率和线性频率关系图,通过关系图可以得出以下分析:当频率在1 000 Hz以上时,Mel频率的分布趋势为对数增长;而频率在1 000 Hz以下时,Mel频率的分布趋势为带宽100 Hz左右的线性分布[8]。

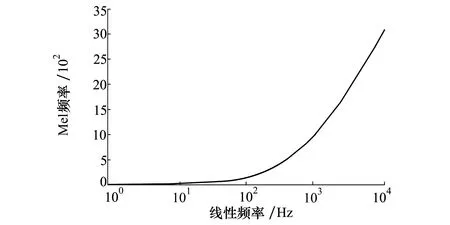
图1 梅尔频率与线性频率的关系

利用倒谱变换进行各个滤波器组输出的幅度与能量之间的强相关性解耦,常见的处理滤波器组输出方法有对数压缩以及余弦变换,得到的Mel倒谱系数的方程如(7)式所示

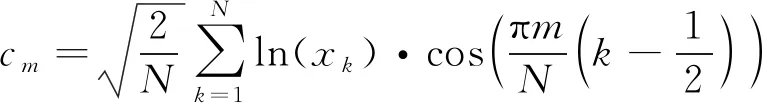
(7)

式中:N为滤波器的个数;m为倒谱系数的维数。

1.2 GFCC提取方法

图2为GFCC特征提取的主要流程。

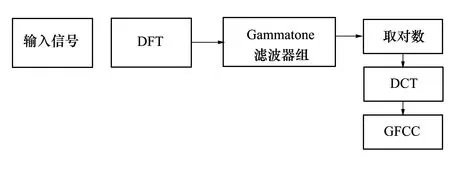
图2 GFCC特征提取流程

具体如下:

1) 分帧。

2) 求能量谱。

对输入信号x(n)使用离散傅里叶变换(discrete Fourier transform,DFT),其公式为

(8)

式中,N为DFT点数。

3) 滤波

鉴于Gammatone滤波器组无限长单位脉冲的特殊响应特性,Gammatone的滤波系数gi(k)可表示为

gi(k)=kn-1exp(-2πBik)cos(2πfi+φi)u(k)

(9)

式中:n为滤波器的阶数;fi为中心频率;Bi为滤波器的衰减因子;φi为滤波器的相位;u(k)为阶跃函数。

将人耳听觉特征临界值作为各个滤波器的带宽从水声信号中提取特征时,可表示为

GEB(fi)=24.7×(4.37fi/1 000+1)

(10)

bi=1.019GEB(fi)

(11)

式中:bi是各个Gammatone滤波器的带宽。

4) 对数运算

样本信号的Gammatone能量谱EG(i)可通过将(8)～(9)式联立取对数的方法获得,表示为

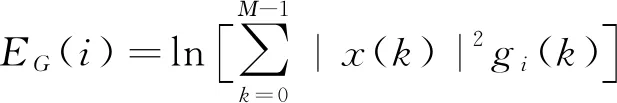
(12)

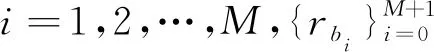
5) 求倒谱

利用离散余弦变换,得到Gammatone系数,其可表示为

0≤n≤Μ-1

(13)

GFCC的计算方法为:求(13)式最大值、平均值、最小值、标准差以及中值等5种统计参数。

2 神经网络构造

2.1 卷积神经网络

CNN的主要思想来自局部连接和权值共享,通过卷积操作实现局部连接,这个局部区域的大小就是滤波器filter。为实现多层网络,需要尽量避免全连接过程中参数繁杂进而造成无法完成计算的问题,同时还可以借助参数共享的方法减少实际运算参数的数量[9]。通常一个普通CNN包括输入层、池化层、激活层、全连接层和输出层等。由于输入层和输出层的外部通常处于不可见状态,故称为隐含层。

2.2 残差神经网络

在确定水下声目标的特征提取方式时,抽取了与目标有关的有效信息，同时也会舍弃许多原始信息,这使得本就难以获取的样本信息没有充分利用。同时这些特征往往受到信道、环境等多种因素的影响,难以保证高度的稳定性[10]。为了保证网络稳定性和原始信息特征的充分利用,往往需要将浅层深度学习网络向深层发展。虽然理论上,假如深层网络B是浅层网络A的恒等映射,那么B至少应当与A性能相同,然而在实际实验中,随着网络的不断加深,网络梯度的不断消失最终会导致深层网络出现退化现象:网络随着深度的增加,在识别率达到饱和后迅速退化[11]。为了解决这个问题,ResNet团队给出了通过设计残差单元的方式有效降低退化现象对系统的影响,其主要思路是通过构建“快捷连接(shortcut connection)”的构建块,将输入信号与经过卷积处理的输出信号恒等映射,从而组成一个残差神经元,其构成的残差网络主要结构见图3。

图3 残差神经网络结构

3 改进的残差神经网络结构设计

基于Inception模块改进的数据池化层是由GoogLetNet在神经框架中首次采用的优化模块,后经过几次版本的迭代,一直到最新的Inception-v4和Inception-resnet,每个版本在性能上都有一定的提升。通过建立小卷积层的串联化,当系统输出来到大卷积层时,基于堆叠替换的方法,拼接多种特征维度层面,来达到提升神经网络学习效率的目的。由于传统残差神经网络的目标是实现百万级以上的大训练样本及多GPU运行的复杂训练,在数据输入时,会将输入到池化层的数据通过7×7的大型卷积层和池化层。在面对具有时变性强的如辐射噪声等类型的时域信号时,如果有效样本有限,则很难利用大卷积层完成数据堆叠,无法有效提升网络的学习效率。因此本文针对基于Inception的模块特点设计了一种改进的数据池化层,这种池化层在面对小样本数据时具有较强的特征提取能力。

为了改进数据池化层,将传统的7×7的卷积层替代为3个3×3的小卷积层,并将每个通道数分别设置为8,16,16。为了有效提升神经网络的特征提取速度,在每个3×3的小卷积层后面都加入了批量标准化和ReLU激活函数。传统加入单一ReLU激活函数的方式,会随着网络层数加深出现过拟合的问题,为了解决这个问题,给每个小卷积层都加入了一个ReLU激活函数,使网络对小样本特征信息的提取能力更强,之后再在Concat层将特征维度拼接到一起。为了避免小样本下网络层数加深可能导致训练过程中过早出现过拟合问题,将改进的残差连接结构加入到数据池化层中,再从最大池化层的输出中提取得到数据特征信息。

4 系统实验分类结果和分析

在本研究中,实地采集舰船辐射噪声样本数据1 756份,取自互联网的海洋生物噪声样本数据877份,利用高斯模拟或水下实测的其他水下噪声样本6 410份。每个样本都被裁剪为大小40帧,帧移15 ms的块,由这些块所组成的数据集统称为样本集(epoch),当样本集过大或根据研究需要时,可以将样本集按照一定数量进行分批(batch),每批大小(batch size)固定。在对样本集做过批处理后,将这些样本分别采用经过改进后的GFCC特征和MFCC特征进行训练, 并使用深层残差神经网络进行目标分类。

在得到匹配本研究的神经元组成结构后,将MFCC和GFCC与残差网络组成的神经元分别进行全样本训练,在多次训练后,对输出求取均值后得到神经网络分类结果,见表1～2。

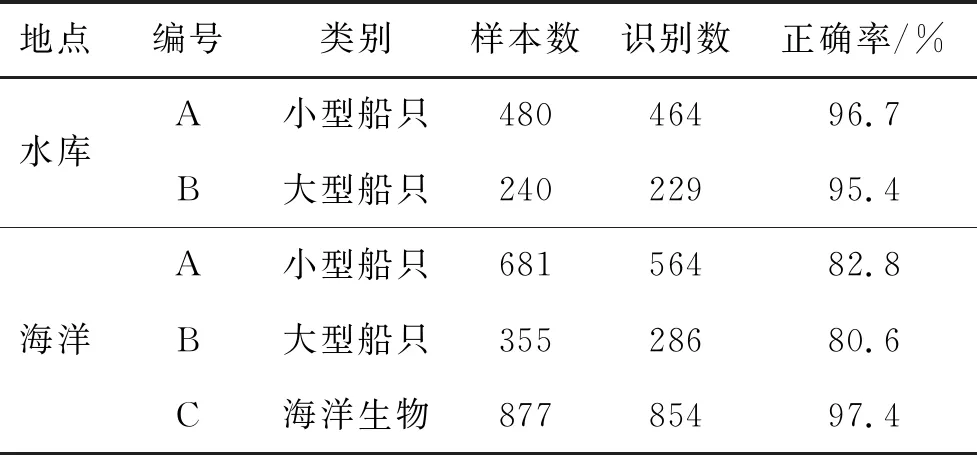
表1 Mel频率倒谱系数特征提取后样本识别统计结果

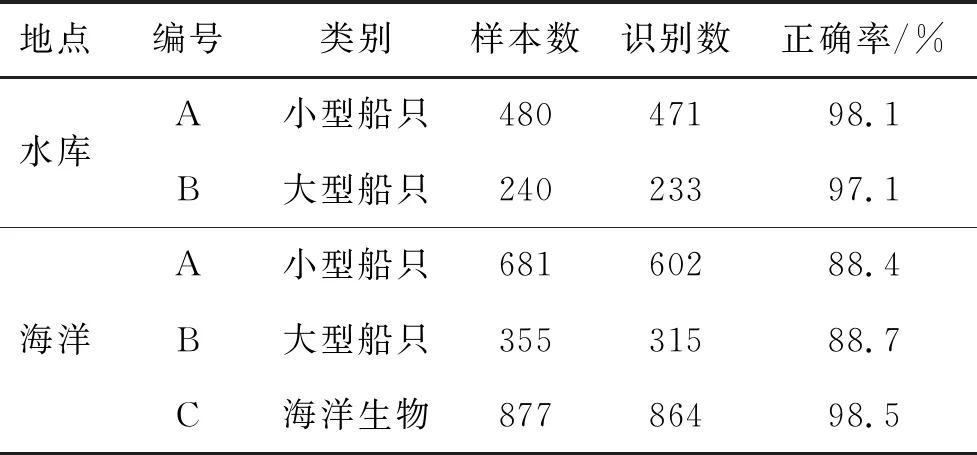
表2 CFCC特征提取后样本识别统计结果

在对分类结果做分析时,由于检测点较多,所以仅展示前10个检测点在前10层网络下的网络预测率和实际识别率。需要说明的是由于动物叫声具有比较显著的声学特征表现[12],考虑到对比的特征较多,工作量较大,所以在样本集中加入了动物叫声作为目标样本,以在合理范围内降低运算参数,增加研究效率。

利用MFCC作为特征提取方法应用在CNN网络中的神经元网络测试结果,如图4所示。图中网络深度表示神经网络的层数,在实验时将特征提取在深度达到每一层时的预测结果标记在图上形成曲线。根据结果可以发现,在网络深度达到5层时,10个预测点的网络预测值趋近于100%,再将被网络贴上标签的识别样本与实际样本集进行对比,得到实际正确率,如图5所示。实验结果表明实际识别率在网络达到6层时出现了明显衰减,且在整个检测过程中实际正确率一直与网络预测值存在着一定的差值,其差值在6层时出现最小值,约为25%左右。

图4 基于Mel频率倒谱系数特征提取的卷积神经网络预测值 图5 基于Mel频率倒谱系数特征提取的卷积神经网络实际识别率 图6 基于Gammatone频率倒谱系数特征提取的卷积神经网络预测值

将基于MFCC改进的GFCC特征提取法应用于CNN网络中,其网络预测值和实际识别率如图6和7所示,可以发现在网络深度达到8层时,网络预测值趋近于100%,与实际识别率相对比,其差值为10%左右,其实际识别率在深度达到9层时出现了明显衰减。

通过研究,对产生这种现象的原因做了如下几点推测,首先,神经网络由于其计算方式不是线性的,在小样本情况下,每一次样本输入进入卷积核后,通过反复卷积-池化-反向传播的计算会产生多个带有不同标签的结果,只有在样本大小匹配网络结构的情况下,网络对权重的选择才会逐渐趋向固定,输出值才会趋向于唯一。另外由于梯度弥散问题,当神经网络深度达到一定值时,梯度衰减过快会导致卷积层内的部分卷积核出现无效化从而出现“卷积核死亡”的问题,可能正是因为这种线性导致了在某层出现的识别率快速衰减的结果。

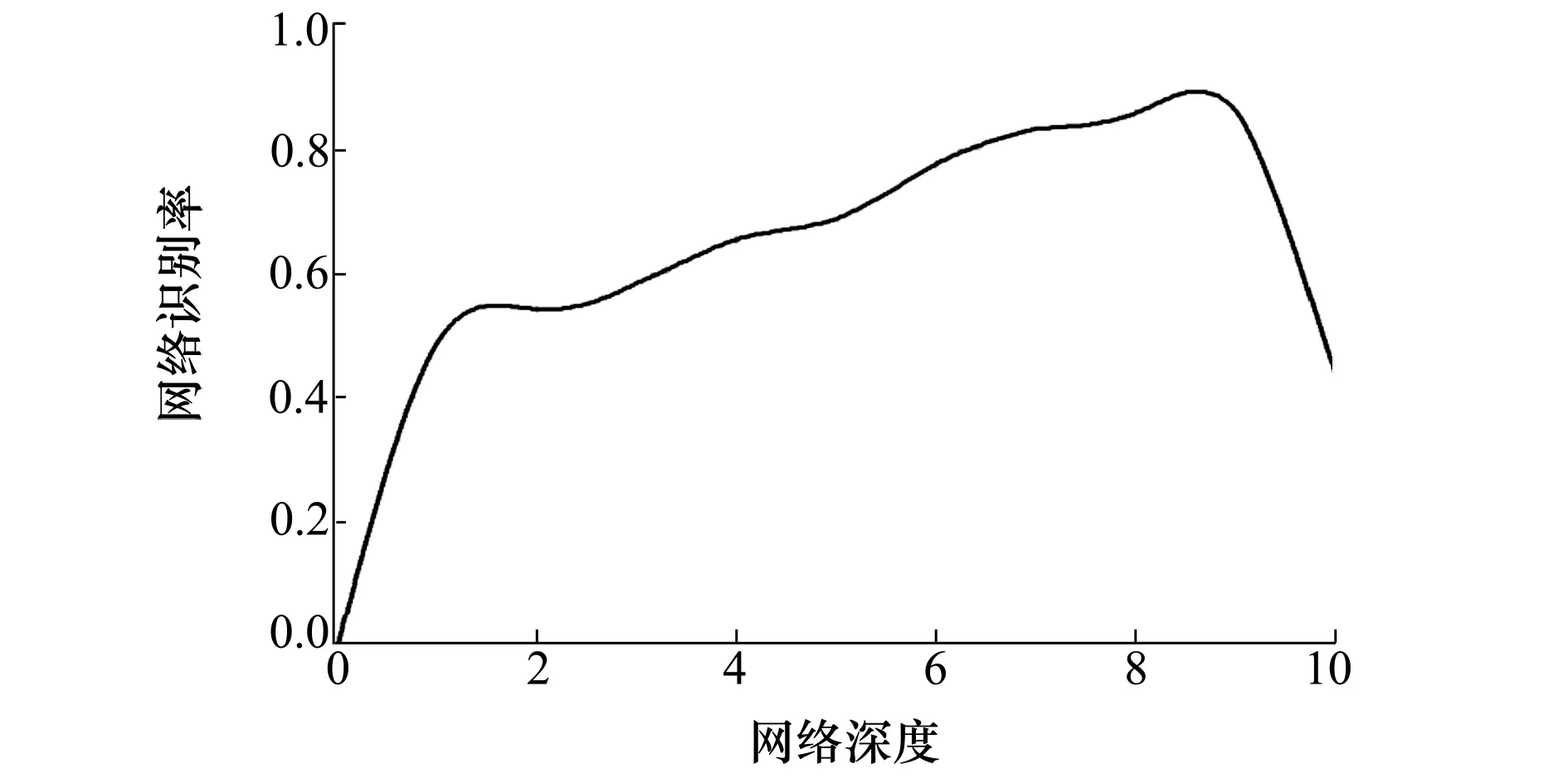
图7 基于Gammatone频率倒谱系数特征提取的卷积神经网络实际识别率

因此,在研究对象为小样本的客观基础上,很容易得到一种直观判断神经元构成的标准,也就是利用输出结果平稳性、神经元死亡深度来判断特征提取法和网络关于本研究的匹配程度,从而决定最终神经元的组成结构。

在文献[11]中发现2015年研发成功的残差神经网络(ResNet)具有比较好的抗噪抗弥散性能,且常被用于(相对)小样本问题的处理上,因此尝试了几种特征提取与残差神经网络的融合,同CNN网络一样,本文将其前10个检测点的10层网络识别数据分别展现如下。

首先是将MFCC与ResNet进行融合,其网络预测值和实际识别率如图8和图9所示,由预测结果图可以看出,当网络深度为7层时,ResNet网络预测值趋近100%,而与实际识别率相对比,其差值最小为20%左右,实际识别率在深度达到7层时出现了明显的衰减。

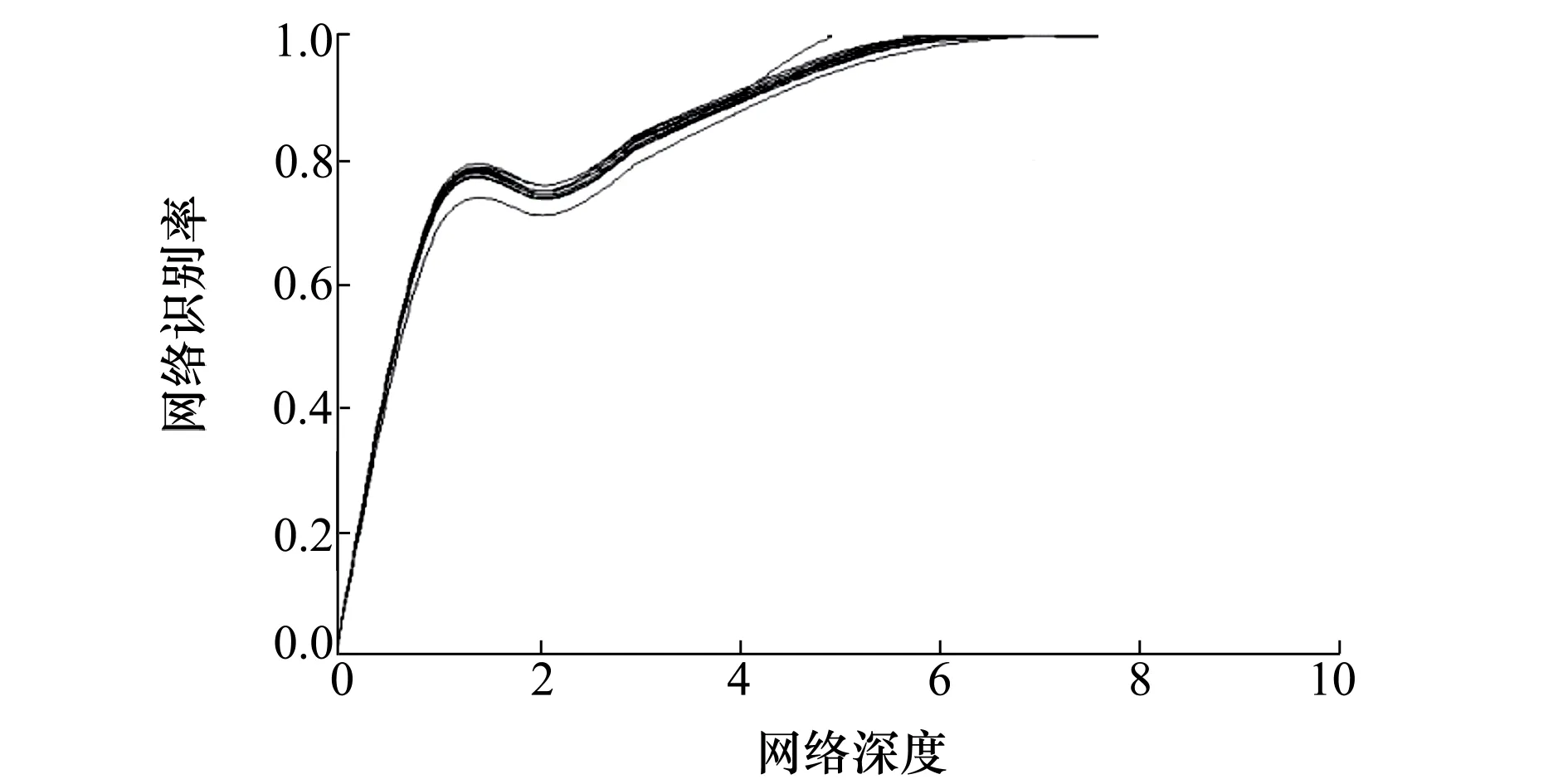
图8 基于梅尔频率倒谱系数特征提取的残差网络预测值

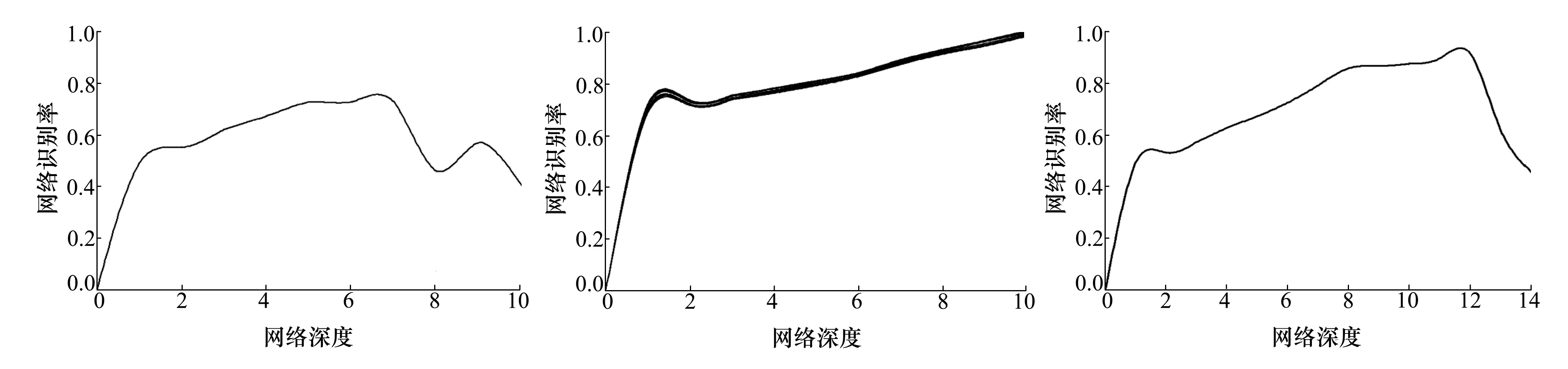
图9 基于Mel频率倒谱系数特征提取的残差网络实际识别率 图10 基于Gammatone频率倒谱系数特征提取的网络预测值 图11 基于Gammatone频率倒谱系数特征提取的实际识别率

将GFCC与ResNet融合,其网络预测值和实际识别率如图10和图11所示,由预测结果图可以看出,该网络在深度为10时虽然接近100%,但仍未到饱和程度,而与实际识别率相对比,其差值为10%左右,为了研究该网络的衰减层数,将该网络的深度加深到15层,可以明显看出,基于GFCC的残差网络在12层时出现了衰减,其实际识别率差值小于10%。

5 结 论

通过研究发现，面向水下目标识别的深度神经网络,其识别稳定性与识别准确率与目标特征提取方法、所选用神经网络模型之间有密切的联系。与常见的浅层水下目标识别神经网络系统相比,利用如改良的残差神经网络等具有较强抗网络退化功能的网络结构,同时选择匹配的特征提取法所组成的网络,可以有效增加网络的深度,提高小样本利用率,增强系统对于多种目标在水下复杂环境中的识别效率。在使用GFCC作为特征提取方法的残差神经网络中,深层网络的识别率和系统稳定性都显著强于使用其他多种组合。这说明,对于基于小样本的水下目标识别系统,在选择特征提取方法和神经网络模型时,应当择优考虑抗噪强,梯度衰减弱,具有强抗退化的种类,以达到网络深层化,以及充分利用有限样本内的各类目标信息的目的。