我国建筑业全生命周期碳排放收敛性研究*
张铮燕 杨晓露 林振思 蔡彬清
(福建工程学院管理学院,福建 福州 350118)
1 概述
近年来,人类活动产生的大量二氧化碳等温室气体,致使温室效应持续加剧,全球性气候问题日益严重,干旱、台风、高温热浪、寒潮、沙尘暴等极端天气频繁发生[1]。为阻止全球变暖趋势,1992年联合国专门制订了《联合国气候变化框架公约》。目前,全球范围内能源及产业发展低碳化的大趋势已经形成,各国积极制定节能减排措施与政策以实现减排目标。
我国是世界上最大的发展中国家,在经济高速发展的同时,能源消耗和碳排放问题也随之而来。我国是世界上最大的碳排放国,占世界能源碳排放总量的28.8%[2]。为了缓解温室效应,保护自然环境,2015年,中国政府在《中美元首气候变化联合声明》及巴黎气候大会上承诺,我国计划于2017年启动全国碳排放交易体系;2020年,习近平主席在第七十五届联合国大会上提出“二氧化碳排放力争于2030年前达到峰值,努力争取2060年前实现碳中和”,“双碳”目标是我国对构建人类命运共同体的庄严承诺。
根据我国建筑节能协会公布的数据,建筑业全生命周期碳排放总量占全国碳排放总量比重超半数,是能源消耗和碳排放的主要来源之一[3]。我国是建筑大国,建筑业是我国重要的支柱产业,减少建筑业能源浪费、降低碳排放量对于建筑业减排和实现我国“双碳”目标具有重要意义。但是我国幅员辽阔,资源分布不均,经济发展水平不同,导致各地区碳排放水平差异巨大,对减排政策的理解和减排行为的实施程度也不尽相同[4]。因此,本文选取2005—2018年中国大陆地区30个省(因数据不全,不含西藏)的建筑业全生命周期碳排放量,并划分出东部、西部和中部三大地区,比较系统、全面地分析全国及各地区的收敛性特征,研究地区间碳排放的差异,找出碳排放的影响因素,提出有针对性的减排建议。
2 研究方法和数据来源
2.1 研究方法
美国著名经济学家Swan[5]和Solow[6]提出了新古典增长模型,指出不同经济体的人均产出会收敛于稳定状态。20世纪20年代中后期,“新经济增长理论”产生,认为各经济体的经济增长并不一定趋于收敛,而且有可能趋于发散。收敛理论从适用于区域经济增长的收敛性研究逐步扩展到其他领域。收敛性检验的方法主要有α收敛、绝对β收敛和条件β收敛三种[7]。
2.1.1 α收敛
α收敛是指不同地区间的研究因素随时间变化逐渐呈现下降趋势,且不考虑研究因素的初始水平和各地区的初始要素结构,是绝对收敛的一种。具体的衡量指标有极差、标准差、差异系数和加权变异系数等[8]。
本文选取差异系数进行α收敛分析,差异系数是样本的标准差与其均值的比值,可以反映数据的离散程度,是一种相对指标,差异系数越大,表示样本的波动程度越大,计算公式为:
(1)
(2)
2.1.2 绝对β收敛
绝对β收敛是指假定各地区具有相同的外部条件,包括相同的人口、资源禀赋、技术水平等,随着时间推移,不同地区间的研究因素将收敛于相同的均衡稳态水平[9]。本文参照Barro及Sala-i-Martin[10]提出的未加入空间效应的传统绝对β收敛方程:
(3)
β=-(1-e-θT)
(4)
式中,T为考察的时间长度,Yi,t+T和Yi,t分别为t+T和t时间内i地区的观察变量,α为常数项,β为收敛系数,θ为收敛速度。若β<0且通过1%、5%或10%水平下的显著性检验,表示研究地区在T时间段内存在收敛趋势,即建筑业碳排放量的增加速度与初始水平成反比,初始碳排放较低的地区相较于初始碳排放较高地区,有着更高的碳排放增加趋势。收敛速度越大,代表收敛于稳态均衡水平的速度越快,计算公式如下:
(5)
2.1.3 条件β收敛
条件β收敛不同于绝对β收敛,考虑了不同地区的人口规模、资源禀赋、技术进步等因素,各地区不会随着时间变化收敛于同一稳定状态,而是有着各自的稳定状态[11]。计算公式如下:
(6)
式中,Xi,t表示各影响因素,βi表示各影响因素的系数。本文参考王娟、张克中[12]和冯博[13]等学者的研究成果,选取城镇化率(X1)、人均GDP(X2)、能源效率(X3)作为碳排放的控制因素。城镇化率是指各地区城市人口数量和地区总人口的比值,是城市化的度量指标[14];人均GDP:换算为以2005年为基期的人均实际GDP,表示经济发展水平;能源效率是指DEA-Malmqusit全要素能源效率,作为反映技术进步的指标。
2.2 数据来源
2.2.1 建筑业全生命周期碳排放
根据既有研究[15-16]计算2005—2018年中国大陆地区30个省份的建筑业全生命周期碳排放量。建筑业全生命周期分为6个阶段,建筑业全生命周期CO2总排放量等于所有阶段的排放量之和,如式(7)所示。
Q=Q1+Q2+Q3+Q4+Q5+Q6
(7)
其中,Q为建筑业CO2总排放量,Q1、Q2、Q3、Q4、Q5、Q6分别代表建材生产阶段、建材运输阶段、建造阶段、运行阶段、拆除阶段和垃圾处理阶段的CO2排放量。每个阶段的CO2排放量根据IPCC推荐的方法进行计算:
Emission=AD×EF
(8)
其中,AD表示活动数据,EF表示排放因子,即单位活动排放量。AD和EF的具体定义在不同阶段有所不同。在材料生产阶段,AD为某一材料的数量,EF为该材料生产时的CO2排放因子。在建材运输阶段和垃圾处理阶段,AD为运输的数量乘以运输距离,EF为某一特定运输方式的排放因子。在建筑施工、运营、拆除三个阶段中,AD为各个阶段各种活动所消耗的能量,EF为某一特定能源(如煤、油、气)的排放因子。
建材消耗量来自《中国建筑业统计年鉴》,各种能源消耗情况数据来源为《中国能源统计年鉴》及CEIC 数据库。各种能源CO2排放因子见表1,我国东部、西部和中部三大地区的划分见表2。
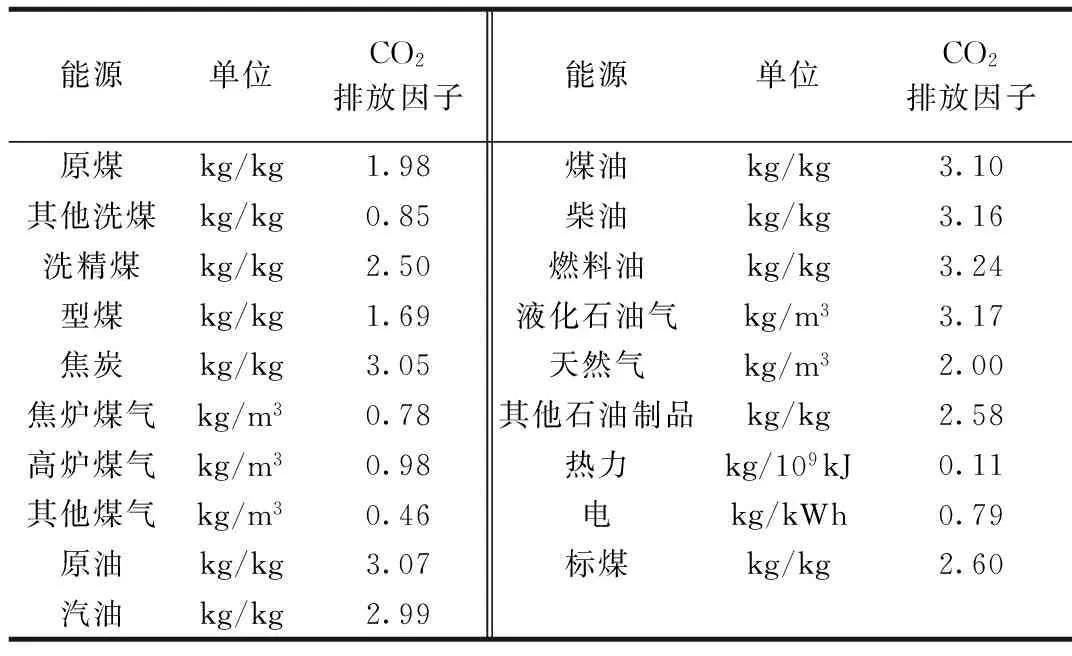
表1 能源CO2排放因子

表2 我国三大地区对应省份
利用以上方法计算得到2005—2018我国各地区建筑业全生命周期CO2排放量,如表3所示。我国建筑业全生命周期CO2排放量整体呈现上升趋势,三大地区建筑业全生命周期CO2排放量的变动趋势基本一致,均在2012年达到最大值,详见图1。
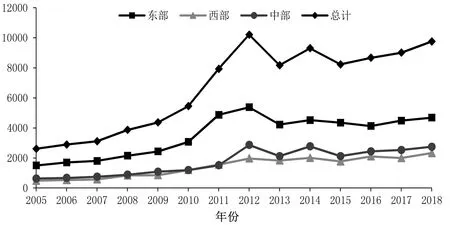
图1 全国及三大地区建筑业全生命周期CO2排放趋势
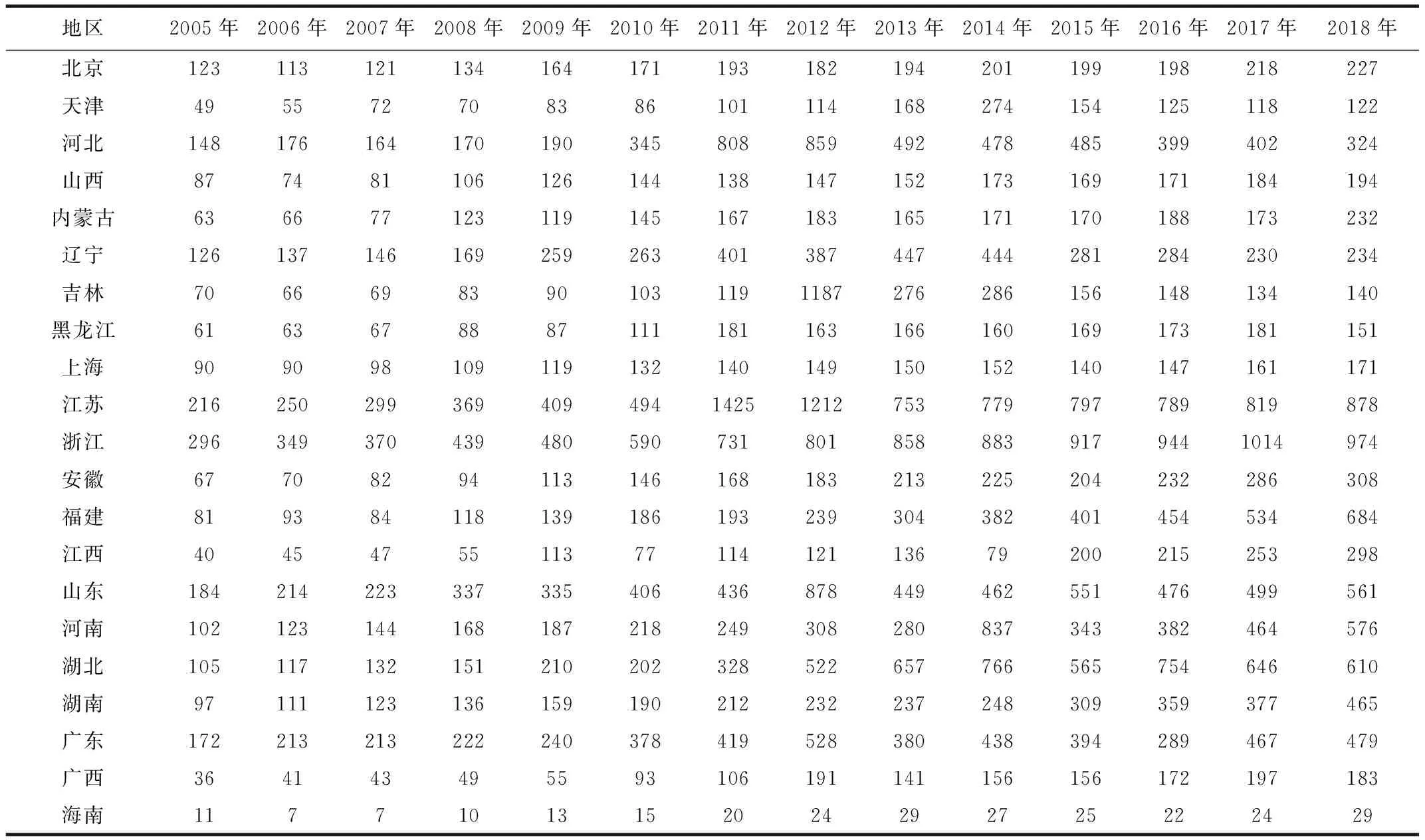
表3 2005—2018年各地区建筑业全生命周期CO2排放 单位:百万吨
2.2.2 DEA-Malmqusit全要素能源效率
以建材消耗量、建筑业能源消耗量、建筑业从业人员、自有施工机械设备年末总功率、建筑业总资产为投入指标,建筑业总产值和竣工面积为期望产出指标,建筑业全生命周期碳排放为非期望产出指标,计算我国各地区的建筑业DEA-Malmqusit全要素能源效率,结果见表4。建材消耗量、建筑业从业人员、自有施工机械设备年末总功率、建筑业总资产、建筑业总产值和竣工面积数据来自《中国建筑业统计年鉴》,建筑业能源消耗量数据来自《中国能源统计年鉴》。
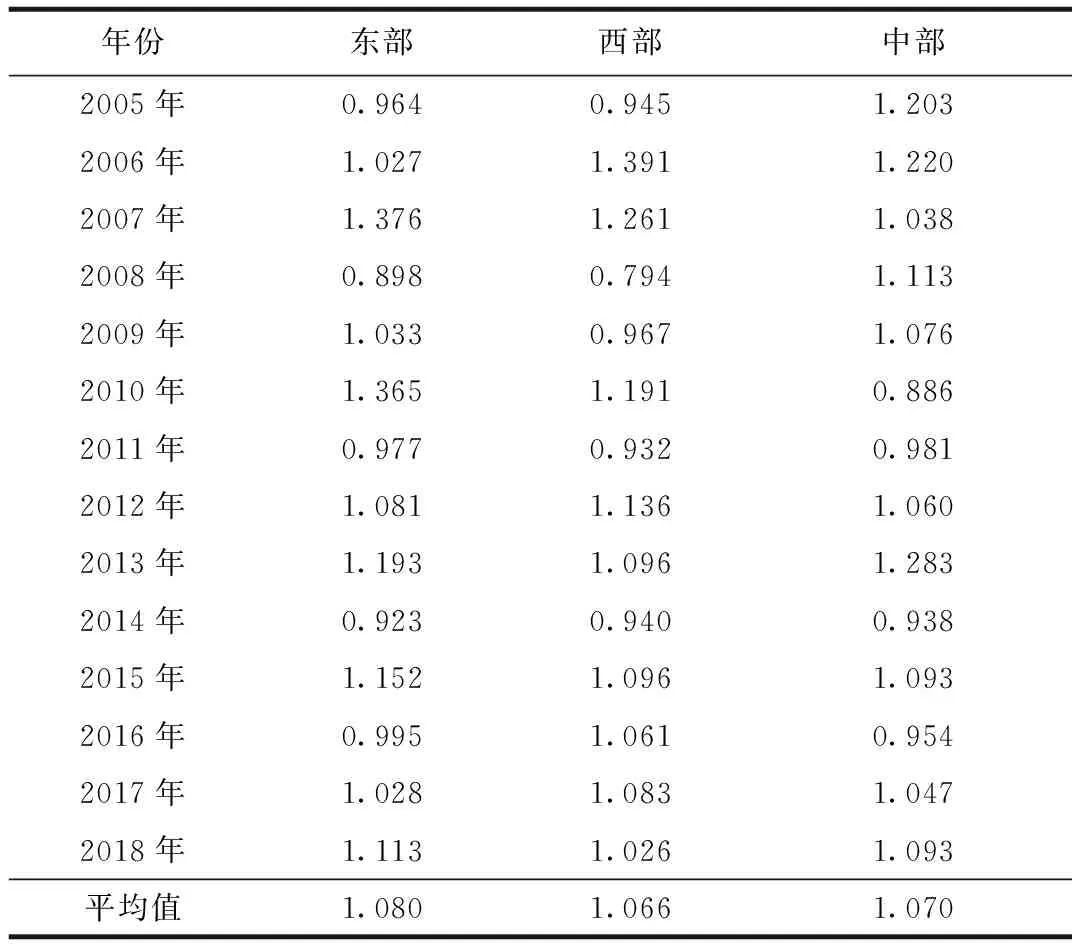
表4 2005—2018年我国三大地区DEA-Malmqusit全要素能源效率
3 我国建筑业全生命周期碳排放收敛性分析
本文采用α收敛、绝对β收敛和条件β收敛对我国及三大地区的建筑业全生命周期碳排放量进行收敛性分析。
3.1 α收敛分析
表5为全国及三大地区建筑业全生命周期碳排放的差异系数值。全国及东部地区的碳排放的差异系数均在2011年达到最大值,为1.10和0.93;西部和中部地区碳排放的差异系数则在2012年最大,为 1.21和1.00。2005—2018年间,全国的差异系数除2005年和2018年为0.74外,其余年份均大于0.74;东部地区的差异系数2005年最小,为0.59;西部地区的差异系数的最小值为0.53;中部地区的差异系数均在0.29以上。除2012年、2014年外,其他年份中部地区的差异系数均为三个地区中的最小值。
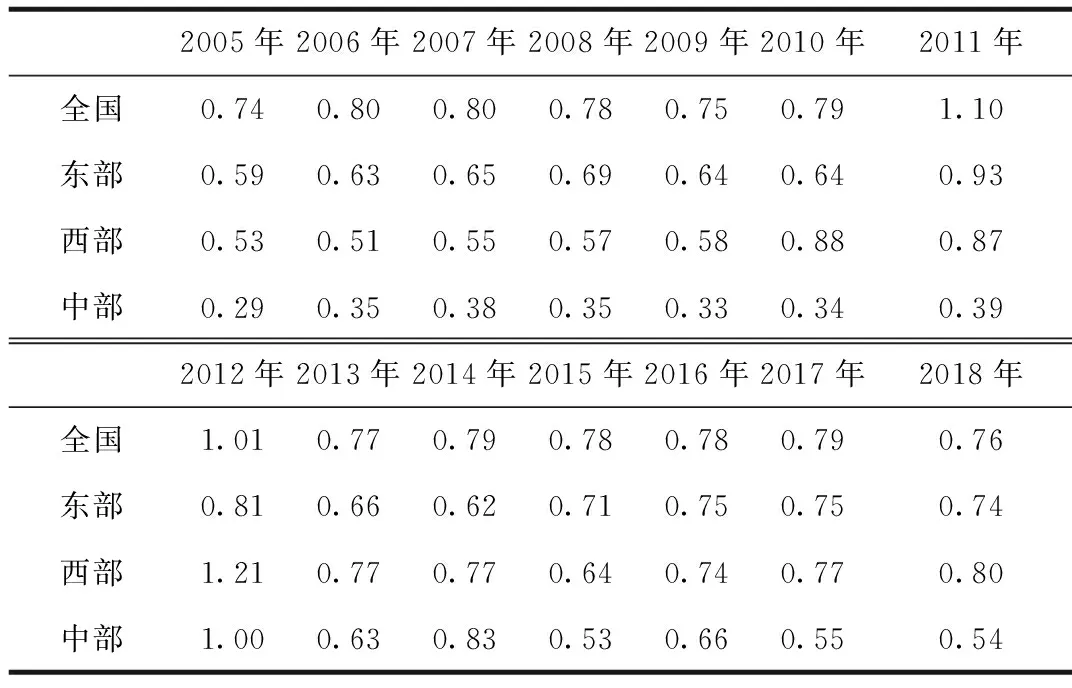
表5 全国及三大地区碳排放差异系数
全国及三大地区碳排放差异系数趋势如图2所示。全国及三大地区差异系数的曲线变化情况基本一致,呈现出缓慢增长,达到最大值后逐渐减小。2005—2009年间全国及三大地区的差异系数呈现出小幅增长趋势,说明全国及各地区的碳排放量处于相对稳定的阶段,不存在α收敛;2010—2013年间,差异系数均大幅度增加,而后又大幅度减少,说明全国碳排放量呈现出区域间不平衡状态,其中2011—2013年间全国及东部地区存在α收敛,2012—2013年间西部和中部地区存在α收敛;2013—2018年间,中部地区的差异系数先后两次达到高峰,但值均小于上一时期;2014—2015年和2016—2017年的中部地区、2014—2015年的西部地区以及2013—2014年的东部地区存在α收敛,相应时间段内各地区的差异系数均呈现出下降趋势。
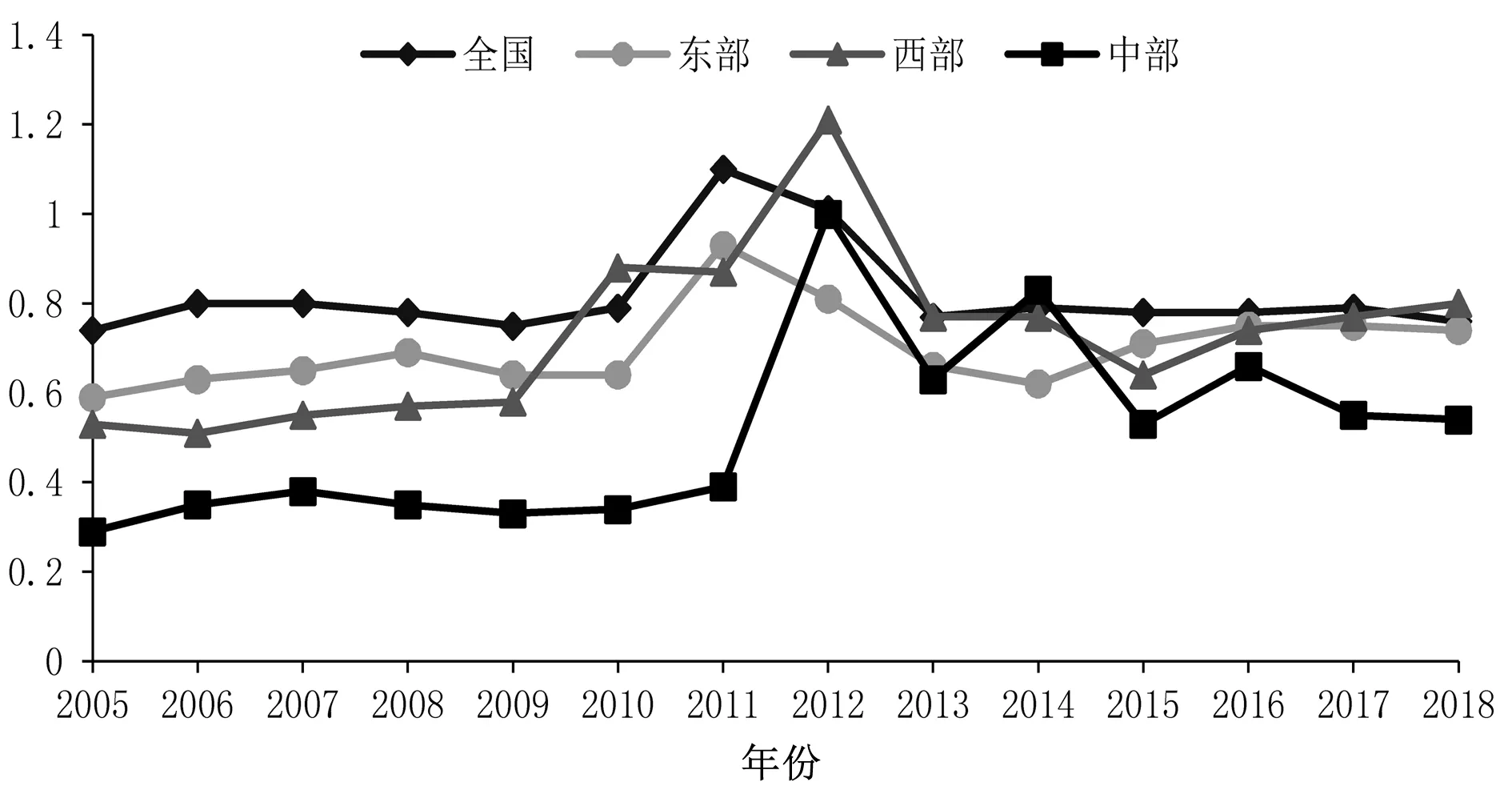
图2 全国及三大地区碳排放差异系数趋势
3.2 绝对β收敛分析
本文采用混合回归模型、固定效应模型和双边固定效应模型检验绝对β收敛的值,混合回归的基本假设是不存在个体效应;固定效应模型表示个体效应与回归变量有较强的关联度,但只能反映随时间而变的变量信息;双边固定效应模型在固定效应模型的基础上,考虑了时间效应,弥补了固定效应模型的不足[15]。
全国混合回归模型的绝对β值为负,通过1%的显著性检验,拟合度为0.0299。固定效应模型的拟合度为0.1326,而双边固定效应模型的拟合度达到了0.3549,是三种模型中的最大值。东部地区在混合回归模型下,不存在绝对β收敛趋势,在固定效应模型和双边固定效应模型的绝对β值为负,分别通过1%和5%的显著性检验,拟合度仍是在双边固定效应模型下达到了最大值,为0.3847。西部地区在混合回归模型下通过10%的显著性检验,固定效应模型和双边固定效应模型均通过1%的显著性检验,且双边固定效应模型的拟合度最大。中部地区模型估计结果均表明存在绝对β收敛,均通过1%的显著性检验,其中双边固定效应模型具有最大的拟合度。通过上述分析可知,双边固定效应模型较其他两个模型更优,因此本文采用双边固定效应模型来检验全国及三大区域的建筑业全生命周期碳排放的收敛性。具体结果见表6。
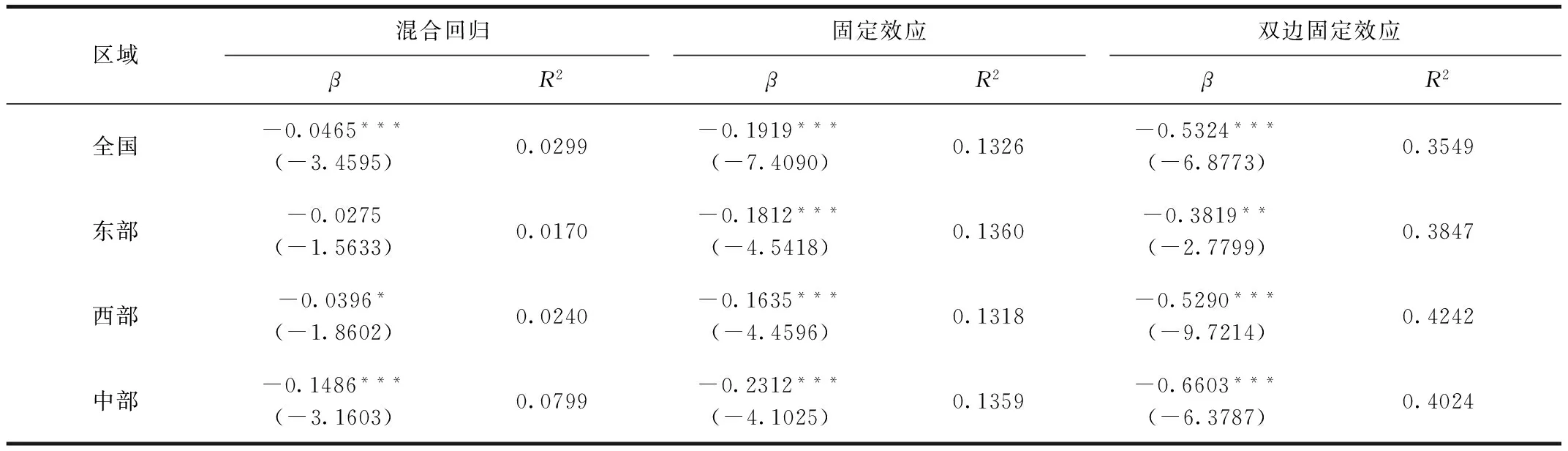
表6 绝对β收敛的三种模型
由表7可知,全国、西部和中部地区的二氧化碳排放量的β值均为负,且均通过1%的显著性检验,东部地区的β值同样为负,通过5%的显著性检验,即全国整体、东部、西部和中部地区建筑业的碳排放量存在绝对β收敛,各地区建筑业碳排放强度的增长与其各自的初始水平呈负相关关系,假设在具有相同外部条件的情况下,全国及三大地区收敛于相同的均衡稳态水平,将形成一致的减排行为。
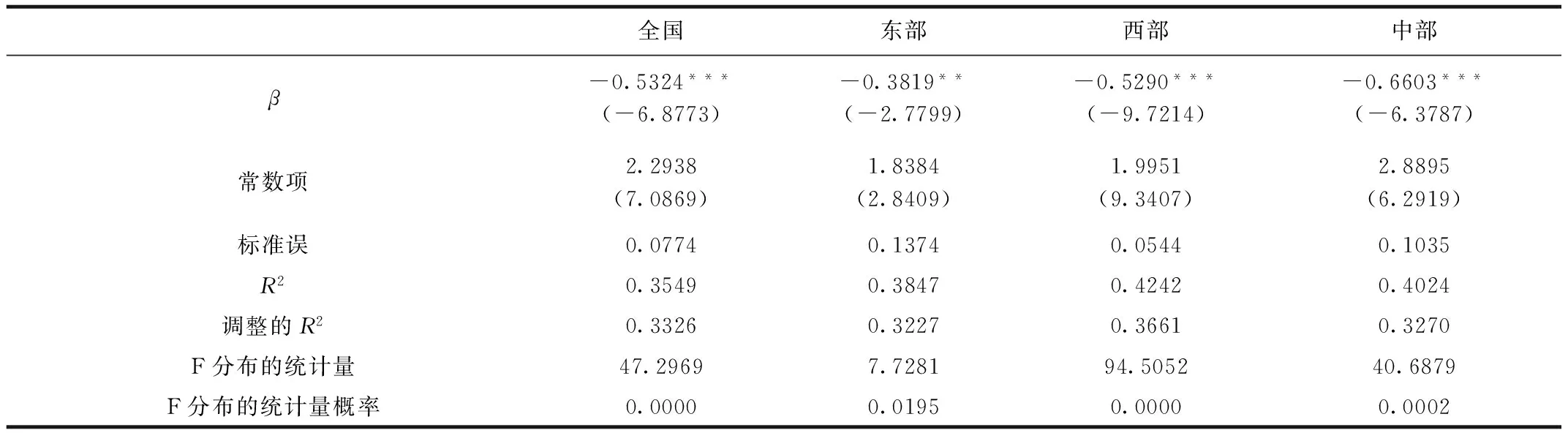
表7 绝对β收敛的双边固定效应模型
根据公式(2)~(5),测算得到全国、东部、西部和中部的收敛速度分别为0.7601、0.4811、0.7529和1.0797。因此,中部地区的收敛速度最快,全国和西部次之,东部地区的速度最小。
3.3 条件β收敛分析
在绝对β收敛模型的基础上,加入城镇化率、人均 GDP 和能源效率三个控制变量,对各变量均取对数,采用面板数据进行检验,得到条件β收敛的结果,见表8。
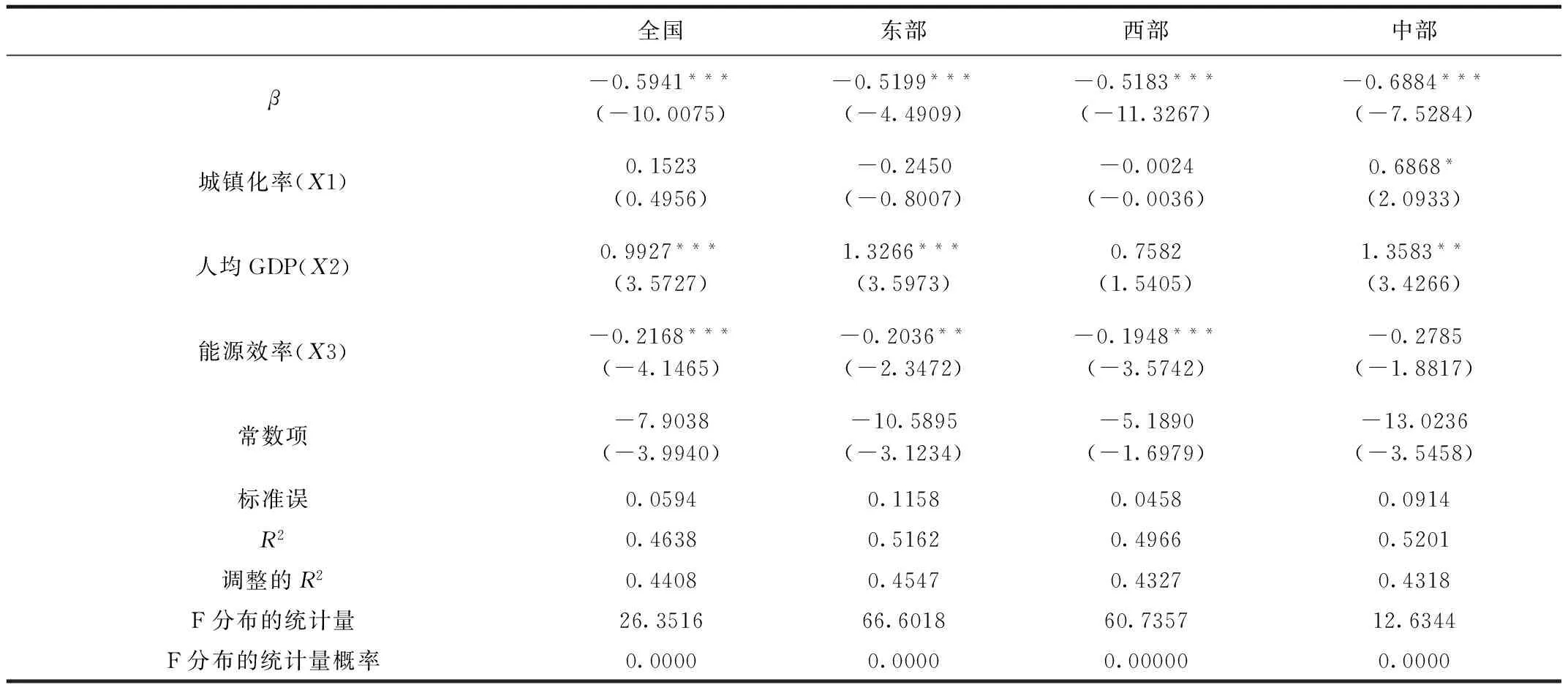
表8 条件β收敛的双边固定模型
全国及三大地区Hausman检验的统计量均为正值,P值均为0.0000,拒绝原假设,证明了采用固定效应模型较为合适,在此基础上加入时间变量,因此,同样采用双边固定效应模型对全国及三大地区的碳排放量进行条件β收敛。加入控制变量后,全国及三大地区的β值均为负,且均通过1%的显著性检验,说明全国及三大地区碳排放存在显著的条件收敛,收敛速度分别为0.8992、0.7338、0.7304和1.1660,相较于绝对收敛的收敛速度,条件收敛的收敛速度有了很大变化,可以看出控制变量会影响碳排放量的变化,并且导致各地区条件收敛的影响因素是不同的。
城镇化率和全国、中部地区的碳排放呈正相关,和东部、西部地区的碳排放关系为负相关,其中,只有中部地区的城镇化率因素通过了10%水平下的显著性检验。城镇化率对东部地区的碳排放影响不显著,主要是由于东部地区经济较为发达,建筑业发展较为成熟,城镇化率高。因此,城镇化率并不是建筑业全生命周期碳排放的主要影响因素,对区域趋同的效果不明显。
人均GDP在全国和东部、西部均通过不同水平下的显著性检验,西部地区除外。这表明人均GDP对全国和东部、西部地区建筑业碳排放均呈现正相关关系。随着人均GDP的增长,碳排放量也随之增长,从而进一步加快区域间的条件收敛,而西部地区人均GDP和碳排放之间的关系不显著。
能源效率和全国及三大地区建筑业全生命周期的碳排放量均为负相关,且只有中部地区未通过显著性检验,这表示能源效率的提高会在一定程度上抑制建筑业全生命周期碳排放的增加,从而逐渐消除区域间碳排放的条件收敛趋势,但中部地区的能源效率未表现出此趋势。
4 结论与建议
结合经济增长理论的收敛概念,本文以我国30个省份的建筑业全生命周期碳排放数据为研究样本,利用α收敛、绝对β收敛和条件β收敛分析模型,对全国及东部、西部和中部三大区域的碳排放的收敛性进行了分析,得出以下结论:
①随着时间的推移,全国及三大区域的变异系数曲线均呈现出缓慢增长,达到最大值后逐渐减小的趋势,说明碳排放的σ收敛仅存在于较少的年份。
②全国及三大地区既存在绝对β收敛,又存在条件β收敛,这说明我国建筑业全生命周期碳排放的空间差异呈现逐步缩小趋势,且这种趋势较为稳固,反映出我国目前碳减排的相关政策和措施取得了一定的成效,并且通过各地区控制碳排放来实现总体碳减排是可行的,应继续推进此举来达到“双碳”目标。
③城镇化率并不是建筑业全生命周期碳排放的主要影响因素。人均GDP对建筑业碳排放呈现出正相关作用,说明人均GDP的增加会促进建筑业碳排放量的增加,加快区域间的条件收敛。能源效率对建筑业碳排放呈现出负相关作用,说明提高能源效率会减缓建筑业碳排放量的增加及区域间的条件收敛过程。我国目前正处于转变经济发展方式、优化经济结构、转换增长动力的攻关期,所以加快经济转型发展、提升能源效率和调整能源消费结构是我国碳减排工作的重中之重。
人均GDP对全国和东部地区的碳排放量呈显著正相关,能源效率和全国和东部地区的碳排放量之间存在显著的负相关。显著影响西部地区碳排放条件收敛的因素只有能源效率,而城镇化率和人均GDP是中部地区碳排放条件收敛的影响因素。由此可以看出,不同地区的条件收敛的影响因素不同,应结合各地区的实际情况,针对性地制定适合各地区的碳减排政策和措施。

