基于节点影响力的理性节点标签传播算法*

皇甫斐斐，杨 阳，邓晓懿,3

(1.华侨大学外国语学院,福建 泉州 362021；2.华侨大学现代应用统计与大数据研究中心,福建 厦门 361021；3.新泽西州立罗格斯大学罗格斯商学院,新泽西 纽瓦克 07102)

1 引言

社区是构成复杂社会网络的重要单元结构，复杂网络中的社区发现有助于揭示真实网络的组织原则、拓扑结构和动力学特性。作为当前的研究热点，社区发现的研究成果被广泛应用在金融、交通和生物等各个领域[1]。目前，主流社区发现算法可分为模块度优化算法和标签传播算法。模块度优化算法源自于Newman[2]提出的模块度概念，通过比较真实网络中各社团的边密度和随机网络对应的子图的边密度的差值来定量度量社团结构的显著性，模块度越大，社区划分效果越好[3]。在此之后，诞生了大量基于模块度的优化算法，如利用模块度增值公式快速定位节点所在社区，可计算大规模网络的Louvian算法[4]；可进行无向和未加权网络划分的基于最大化加权模块度的社区发现算法[5]；能部分解决分辨率限制和极端退化问题的结合节点亲密度和节点度的模块度优化算法[6]；可根据不同节点划分，以及结合深度学习和模块度优化的DNR (Deep Nonlinear Reconstruction)[7]和ComE (Community Embedding)[8]算法进一步提升整体网络模块度的动态社区发现算法[9]。但是，基于模块度的算法并不能真实反映社区划分。

因此，基于标签传播算法LPA(Label Propagation Algorithm)[10]的快速社区发现算法应运而生。LPA思路简单，具有线性时间复杂度，可有效处理大规模复杂网络等优点。LPA的出现引起了大量关注,接着研究人员提出了一系列扩展算法，例如Leung等[11]提出的异步标签传播算法，可解决LPA算法在二部网络中震荡不收敛问题。LPAm(Label Propagation Algorithm specializing modularity)[12]通过寻优模块度进行标签更新，降低了LPA的随机性，但存在易陷入局部最优的缺点。LPAm+[13]结合了多级贪婪集聚算法，避免了LPAm的缺点，可进一步提高划分模块度。LPA-S(Stepping Label Propagation Algorithm)[14]先根据节点相似性更新节点标签、划分初始社区，然后根据社区相似性合并社区，可获得更好的社区划分。由于将模块度作为优化条件可能导致和真实社区划分结果有偏差，部分研究将节点度和边的权重引入标签更新过程，以解决节点更新标签的随机性和无序性。比如LPAp(Label Propagation Algorithm with importance quantification)[15]根据节点PageRank值找到k个核心节点，分别为每个核心节点分配一个社区标签再进行标签扩散，降低了LPA算法结果的不稳定性。NIBLPA(Node Influence Based Label Propagation Algorithm)[16]通过k-shell值将节点重要程度排序作为节点标签更新顺序，并通过计算标签的重要程度，避免了当节点遇到出现次数最多的标签不止一个时随机选择的问题。CenLP(Centrality-based Label Propagation)[17]则重新定义了节点中心值和偏向值，通过节点中心值和偏向值计算局部高密度近邻节点的相似性来改进标签的选取和传播过程。上述算法中的标签传播和更新都是发生在邻居节点之间，但是对于复杂网络的小世界性质，节点之间信息交换并不只发生在相邻的节点之间。此外，社区网络结构的明确程度可通过网络平均集聚系数反映，集聚系数越大，网络拓扑结构越清晰；反之，网络拓扑结构则越模糊。如何在拓扑结构相对模糊的网络中提高社区划分精度也是当前的研究热点[5]。

为解决上述问题，本文提出基于节点影响力的理性标签传播算法RLPBNI(Rational Label Propagation algorithm Based on Node Influence)。RLPBNI首先将节点影响力作为标签更新顺序的依据；然后，引入理性节点的概念，假设节点可充分掌握网络的局部和全局信息，并以理性思维方式选择对它影响力最大的节点的标签作为更新标签，可兼顾拓扑结构不同的网络；最后，根据社区重叠度对社区进行降维处理，进而提高社区划分的精度。

2 相关理论

2.1 LPA

LPA是基于网络拓扑结构的社区探测算法，主要思想是通过连接关系进行标签传递。在初始状态，每个节点被赋予唯一标签，每一次传递过程中，节点将自身标签传递给邻居节点，同时接受来自其他邻居节点传递的标签，并选择出现次数最多的标签作为自身更新标签。如果出现次数最多的标签不止一个，那么节点随机选择其中一个标签进行更新。不断重复该过程，直至网络中每个节点的标签不再变化，此时，具有相同标签的节点形成一个社区。

但是，LPA在多次迭代之后无法保证收敛性，当算法采用同步更新标签的方式时，t步标签与t-1步标签相关，在二部网络中会存在震荡收敛的情况。除此之外，LPA还存在以下2个缺点：

(1)不稳定性：节点更新的无序性造成不同更新顺序可能得到不同的社区划分结果；

(2)随机性：当节点的最大标签数不止一个时，节点会从中随机选择一个进行标签更新，可能会产生雪崩效应，难以保证社区划分精度。

总体来说，标签传播算法简单易于理解，未来也可应用在大规模复杂网络中，如何控制LPA的稳定性和随机性是亟待解决的问题。

2.2 节点影响力算法

常见的节点重要度度量指标有度中心度、介数中心度和k-shell中心度[18]。度中心度只反映节点局部特征；而介数中心度只反映全局重要程度，且计算复杂，不能应用在大规模网络中；k-shell中心度可通过不断删除外层节点找到核心节点，在删除节点的过程中直接去掉某些重要的边，并将同一批次删除的节点视为同等重要，其结果并不能准确反映节点重要程度。

节点影响力算法[15]则认为节点之间的相互影响并不只发生在相邻节点之间，且在相同路径长度下，一个节点到达另一节点的路径条数越多，影响力越大。设网络G=(V,E)中存在M个节点，N条边，其中，V表示节点集，E表示边集。邻接矩阵为A=A(i,j)M×M，如果节点i和节点j直接相连，A(i,j)=1；否则，A(i,j)=0。 节点间影响力用Fk(i,j)表示(即节点i对节点j的k步路径影响力)，其等于节点i在长度为k的链接路径下到达节点j所遍历的节点数量，如式(1)所示：

(1)

其中，节点i对节点j的1步路径节点间影响力F1(i,j)=A(i,j)，节点i对节点j的k步路径节点间影响力为Fk(i,j)，l为网络中任意节点。若Fk-1(i,l)和A(l,j)同时非零，表示节点i可通过节点l对节点j施加影响力，相当于k步路径节点间影响力Fk(i,j)在Fk-1(i,l)的基础上增加了一个遍历节点l。

已有研究[18,19]发现，当k等于网络中任意2个节点间的最短距离(即网络直径)时，标准化节点影响力值可以达到收敛状态。节点影响力算法不仅考虑了节点的全局特性，而且模拟网络中信息传播真实过程，可以更有效地识别网络中具有影响力的重要节点。

3 基于节点影响力的理性标签传播算法

3.1 相关定义

定义1(节点间整体影响力Inf(i,j)) 基于节点影响力定义，节点i对节点j的整体影响力等于两者之间1～k步路径节点间影响力之和[19]。不同路径长度下节点间影响力的权重不同，路径长度越长，对应的权重越小，计算公式如式(2)所示：

(2)

其中，Fk(i,j)是节点i对节点j的k步路径节点间影响力；K表示节点间影响力的最长路径数，K值通常设为网络直径；参数λ因网络结构而异。

定义2(节点间整体影响力矩阵INF) 与邻接矩阵类似，网络中任意2个节点间的整体影响力Inf(i,j)可组成节点间整体影响力矩阵，即INF=Inf(i,j)M×M。节点i到其他节点的节点间整体影响力构成了INF的第i个行向量INFi。

定义3(理性节点) 理性节点的概念借鉴了经济学中理性人假设。理性节点定义为，在标签传播过程中可以感知其他近邻节点对其自身影响力大小，进而选择对自身影响最大的节点的标签作为本轮新标签进行更新的一类节点。

定义4(社区重叠度COD(Ci,Cj)) 社区Ci与Cj的重叠度等于Ci和Cj重叠边的数量与Ci和Cj中节点所连接边总数的比值，公式如式(3)所示：

(3)

其中，Eo(Ci,Cj)表示社区Ci和Cj重叠边的数量，Ec(Ci,Cj)表示Ci与Cj中节点所连接边的总数。

3.2 算法流程

RLPBNI包含3个步骤，其流程如图1所示。

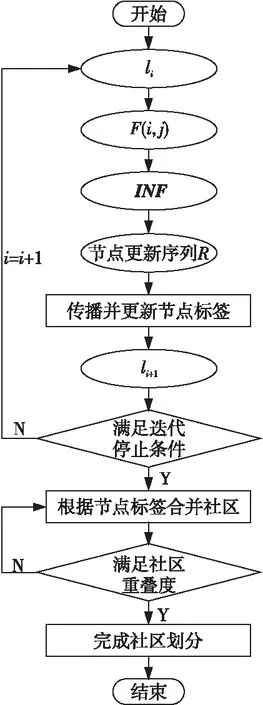
Figure 1 Procedure of RLPBNI

(1)计算节点间影响力F(i,j)，并基于F(i,j)计算节点整体影响力Inf(i,j)，进而得到矩阵INF。然后，将节点按照整体影响力的降序排列作为更新顺序。

(2)初始化节点标签li，此时每个节点标签编号唯一，按照更新顺序，对于每个节点找到对它影响力最大的节点的标签作为更新标签，重复这一过程直到每个节点标签不再变化时，停止更新。将具有同一个标签的节点归为一个社区，得到初始候选社区。

(3)如果初始候选社区之间重叠度大于阈值，则将该2个社区进行融合，直到所有社区之间重叠度都小于阈值，得到最终社区划分结果。

3.2.1 节点更新序列初始化

本文首先计算节点影响力，按照由大到小的顺序对节点影响力排序，并将其作为度量节点重要程度的依据。首先，根据式(1)计算k步路径节点间影响力Fk；然后根据式(2)求得节点整体影响力INF，将节点按整体影响力由大到小排序即可得到初始节点序列L，流程如算法1所示。

算法1节点序列初始化

输入：邻接矩阵A，路径长度K，参数λ。

输出：整体影响力矩阵INF，初始节点序列L。

1.INF=0M×M，F1(i,j)=A(i,j)，L=∅；

2.Fork=1 toK

3.CalculateFk(i,j) according to equation(1)；

4. CalculateInf(i,j) according to equation(2)；

5.EndFor

6.INF=(Inf(i,j))M×M；

7.Fori=1 toM

8.Li=sort{INFi}，L=L∪Li；

9.EndFor

3.2.2 标签传播

假设网络中的节点都是理性节点，可获得近邻节点的完全信息，那么节点会选择近邻节点中对它影响最大的节点标签作为本轮更新标签。如果对该节点影响最大的节点存在2个或2个以上，则选取与该节点距离最短的节点。若对该节点影响最大，且距离最近的节点存在2个，则从中随机选择一个节点。按照标签更新顺序重复迭代，直到每个节点的标签不再发生变化时，迭代停止。之后，将具有相同标签的节点归为一个社区，得到初始候选社区。算法流程如算法2所示。

算法2标签传播

输入：网络G，节点间影响力F，节点序列L，社区划分数q。

输出：初始候选社区C。

1.Label={l1,l2, …,lM}；

2.Whileeach node’s labelliis not unique

3.ForeachLi∈L

4.MaxInf=max{F(i,1),…,F(i,M)}；

5.Ifcount(MaxInf) > 1

6.Ifcount(nearest(MaxInf)) > 1

7.Random select a nodeF(i,t)；

8.F(i,j)=F(i,t)；

9.Li=Lj；

10.EndIf

11.Endif

12.EndFor

13.EndWhile

14.If(C1∩…∩Cq=∅ andCiis unique)

15.C={C1,C2,…,Cq}；

16.EndIf

3.2.3 社区合并与更新

计算候选初始社区之间的重叠度，将重叠度高于阈值的2个社区中较小的社区合并在较大社区中，再次计算新社区之间重叠度，直到所有社区之间的重叠度不大于阈值，迭代停止。

算法3社区合并与更新

输入：初始候选社区C，重叠度阈值a。

输出：最终社区划分COM。

1.WhileCOD(Ci,Cj) >a

2.ForeachCi∈C

3.D=max{COD(Ci,C1),…,COD(Ci,Cq)};

4.IfD>a

5.COD(Ci,Cj)=D;

6.Ci=Ci∪Cj;

7.DeleteCjfromC;

8.EndIf

9.EndFor

10.EndWhile

11.COM←C;

3.3 算法复杂度分析

假定网络中有M个节点和N条边，K为网络直径，S是理性节点标签传播所得初始社区数，那么：

(1)计算节点影响力的时间复杂度为O(KM2)；

(2)理性节点标签传播过程和LPA传播过程相似，整个传播过程的时间复杂度为O(N)；

(3)社区相似性计算的时间复杂度为O(S2)。

因此，本文RLPBNI的时间复杂度为O(KM2+N+S2)。由于K和S的取值通常远远小于M，因此O(KM2+N+S2) ～O(M2)。

4 实验与结果分析

4.1 实验设置

为验证RLPBNI的有效性，本文采用真实网络(Karate、Dolphins及Football)[20]及人工基准网络LFR(Lancichinetti Fortunato Radicchi)[21]进行验证实验，评价指标则选取模块度Q、标准互信息指标NMI(Normalized Mutual Information)[22]和调整兰德指标ARI(Adjust Rand Index)[23]3种。对比算法则包含FN(Fast Newman)、LPA、NIBLPA和CenLP 4种。

模块度是评价社区发现算法性能的常用指标，用于衡量社区结构性的强弱，Q越接近 1，社区划分精度越高，其对应的社区结构性越强，计算公式如式(4)所示：

(4)

其中，N为网络中的总边数，A表示网络所对应的邻接矩阵。如果节点i和节点j直接相连，Aij= 1；否则，Aij=0。di和dj分别为节点i和节点j的度，li和lj分别表示节点i和节点j的标签，如果li=lj，则δ(li,lj)=1，否则为0。

NMI和ARI指标用于度量社区划分结果与标准(真实)社区结构的相似度，如式(5)和式(6)所示：

(5)

(6)

其中，Ni和Nj分别表示算法结果序列中社区Ci的节点个数和真实划分序列中社区Cj的节点个数，Nij表示社区Ci和Cj的公共节点个数，m和n表示结果序列和真实序列的长度，M表示节点个数。NMI的取值为[0,1]，其值越大说明互信息化程度越高，2个序列越相近。ARI指标与NMI类似，取值亦为[0,1]，其值越大，2个序列相似程度越高。

4.2 真实网络实验结果与分析

4.2.1 Karate数据集

Karate网络是通过对某一美国大学空手道俱乐部进行观测而构建出的一个含有34个节点的社会网络。Karate网络中的节点表示俱乐部成员，其中包括俱乐部经理、教练和学员；边则表示成员之间的关系或联系。由于俱乐部经理和教练之间产生意见分歧，俱乐部成员之间逐渐形成以教练和经理为首的2个社区。RLPBNI的社区探测结果如图2所示，本文用黑色虚线区分左下和右上2个社区。从图2中可看出，节点1和节点34分别处在2个社区中心，表示俱乐部经理和教练，NMI值为1，说明RLPBNI划分结果与真实社区划分结果完全一致。

Figure 2 Community detection result on Karate

4.2.2 Dolphins数据集

Dolphins网络描述了1994～2001年生活在新西兰海峡间的宽吻海豚之间的联系，网络中节点表示海豚，边则表示2只海豚间关系，共包含62个节点和928条边。本文算法将Dolphins网络划分为2个社区，结果如图3所示。RLPBNI的NMI值为0.881 9，其结果只有1个节点和真实社区划分不一致，算法将节点SN89(图中箭头所指节点)划分到了左侧的社区中。SN89只有2条边，分别连接了左侧社区中的节点Web和右侧社区中的节点SN100。Web的节点度为9，SN100的节点度为7。从图3中可知，由于Web所在局部结构中节点连接更加紧密，对SN89的影响路径条数大于对SN100的，因此本文算法将SN89划分到节点Web所在的社区。

Figure 3 Community detection result on Dolphins

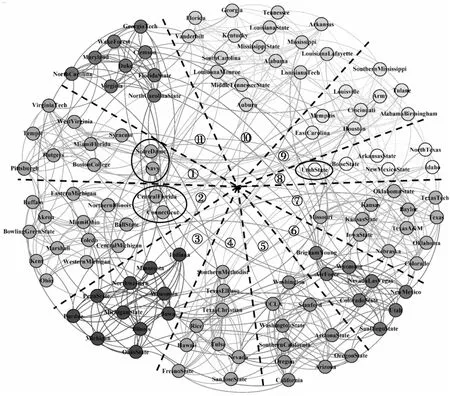
Figure 4 Community detection result on Football

4.2.3 Football数据集

Football足球俱乐部网络由2000年美国大学生足球联赛数据抽象而成，网络中每个节点表示一个足球队，每条边表示2支队之间进行过的一场比赛，每个球队都隶属一个联盟，联盟内部球队之间比赛次数多于非联盟球队之间比赛次数，共有112支球队，12个联盟，613场比赛。应用RLPBNI对Football网络进行划分，得到11个社区，在图4中分别用①～表示。

Navy、NotreDame、UtahState、Connecticut和CentralFlorida这5支球队(图中椭圆所圈节点)本属同一个联盟，但该联盟节点松散，内部赛事较少。Navy和NotreDame这2支球队与①号联盟间的关系更为紧密，Connecticut和CentralFlorida与②号联盟的球队之间的比赛更多，UtahState与以上4支球队未曾有过接触，但与⑧号联盟的球队有过多次较量。根据节点连接紧密程度和节点影响力，RLPBNI将5支球队划分给其他联盟，最终得到11个联盟，但NMI值仍然高达0.909 5，比其他4种算法的精度更高。

由于3个真实网络的集聚系数皆大于0.2，为方便性能对比，RLPBNI的参数λ取值设为0.2～0.3，K等于对应网络直径。5种算法在3个真实网络上进行社区划分的平均模块度Qavg和NMI结果如表1所示。在Qavg指标方面，NIBLPA和RLPBNI 2种算法分别在Karate网络上获得了最优值(0.404 3)和次优值(0.401 2)，FN的结果最差；而RLPBNI和CenLP则在Dolphins和Football 2个网络上分别得到最优值(0.533 4，0.626 3)和次优值(0.526 6，0.609 7)，LPA在Dolphins网络上的平均模块度最低，FN在Football网络上的社区划分效果最差。在NMI指标方面，本文提出的RLPBNI在所有真实网络上皆得到最优结果，其中在Karate网络上的结果和真实划分结果一致，在Dolphins和Football网络上的NMI值均高于其他算法的，也非常接近真实结果。NIBLPA的社区划分结果次之；FN算法的划分结果总体较差，这是因为FN算法是将模块度系数作为优化目标，而没有考虑得到的社区划分结果和真实社区划分的相似性。

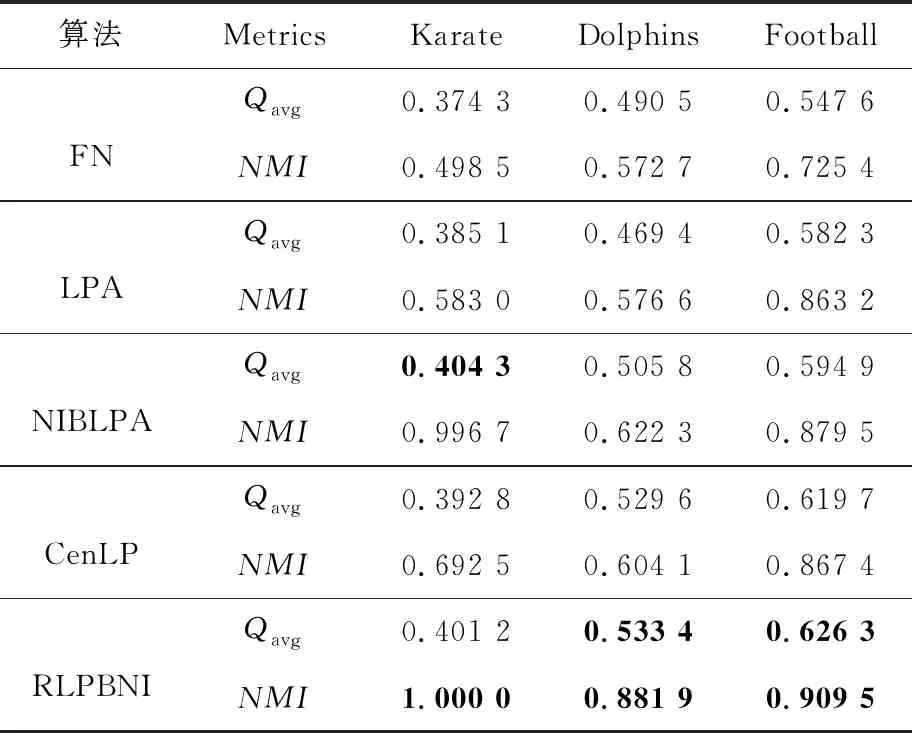
Table 1 Results comparison of five algorithms on real-world networks

4.3 人工合成网络实验与结果分析

LFR模型通常用于生成人工合成网络，该模型生成的人工网络的节点度和社区规模均服从幂律分布，更接近现实生活中的网络结构，且可通过改变可调节参数控制生成不同社区结构的网络数据，一般用于测试社区发现算法的性能。本节实验共生成2个人工网络，具体参数设置如表2所示。

Table 2 Parameter settings of LFR synthetic networks

在表2中，M表示网络中节点个数;p和pmax分别表示网络的平均度数和最大度数;Nmax和Nmin分别表示社区的最大和最小节点数;μ为网络混合系数，其值越大，网络结构越模糊，社区划分结果越不明显。

5种算法在Net1和Net2网络上的NMI与ARI结果分别如图5和图6所示。图中横坐标为网络混合系数μ，μ以步长0.1从0.1增加到0.9，纵坐标是相应算法的社区划分结果与真实社区划分之间的接近程度(NMI与ARI)。从图5和图6中可看出，随着μ值增加(即网络结构的复杂程度提高)，5种算法的社区划分精度不断降低，对应划分结果的社区结构越来越模糊。当μ≤ 0.5时，FN的精度随着μ的增加不断降低，其他4种算法的精度接近于1，且基本持平；当μ>0.5时，NIBLPA、LPA、CenLP和RLPBNI的社区划分精度开始降低，其中前三者的精度下降速度较快，而RLPBNI精度的下降速度则相对平缓，而且在不同网络上皆优于其他4种算法，说明该算法能够有效地发现社区边界比较模糊的网络结构。

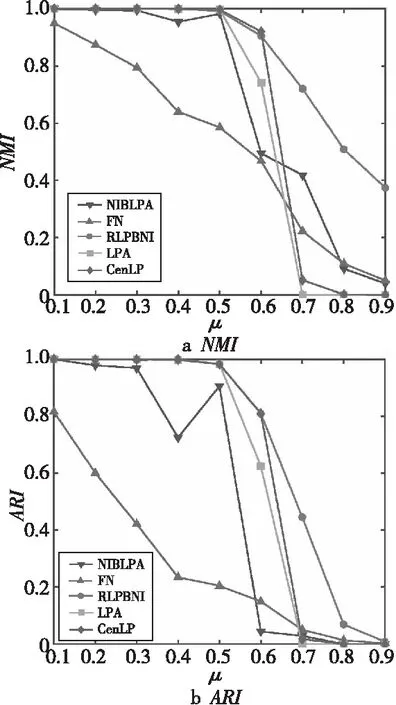
Figure 5 Comparison of NMI and ARI on Net1

Figure 6 Comparison of NMI and ARI on Net2

4.4 参数灵敏度分析

NIBLPA的社区划分效果在很大程度上依赖参数K和λ。K为节点间影响力最长路径，也就是对整个网络计算传播影响力的上限估计。K≥1，最大值是2个节点之间最长路径，2节点间最长路径显然可以无穷大，由于计算复杂度高，本文假设在不影响算法效果的前提下，K越小越好。λ为可调节参数，对不同路径长度下节点间影响力进行权重分配。λ越大，路径长的节点间影响力获得的权重较小。

4.4.1 参数K灵敏度分析

由于RLPBNI在Net1和Net2网络上的划分效果相近，本文仅使用Net2网络分析K的灵敏度，并讨论K对算法的影响效果。网络混合系数μ=0.6，网络直径为6，实验结果如图7所示。

Figure 7 Parameter sensitivity (K) of RLPBNI on Net2@0.6

在图7中，2个子图的x轴和y轴分别代表可调节参数λ和路径长度K，z轴表示网络划分的相似度指标NMI和ARI，颜色越浅则表示划分相似度越低，颜色越深则反之。参数K和λ的取值分别为{1,2,…,10}和{0.1,0.2,…,1}。从图7中可以看出，对于不同取值的λ，K值的变化对NMI和ARI的整体影响很小，特别是当λ∈[0.1,0.4]时，K值大小对结果基本上没有影响；当λ∈(0.4,0.6]时，K值变化使NMI和ARI值产生微小的波动；当λ∈(0.6,1]时，K值变化会带来相对较大的NMI和ARI值波动，但在可接受范围之内。总体来看，当λ值确定且K取值为网络直径时，NMI和ARI可以得到最优结果。

4.4.2 参数λ灵敏度分析

为分析网络上λ的取值范围，将RLPBNI应用在3个真实网络和人工网络Net2上，并将K值固定为每个网络对应的网络直径，直接讨论λ与相似度指标NMI和ARI的关系。实验结果分别如图8和图9所示。

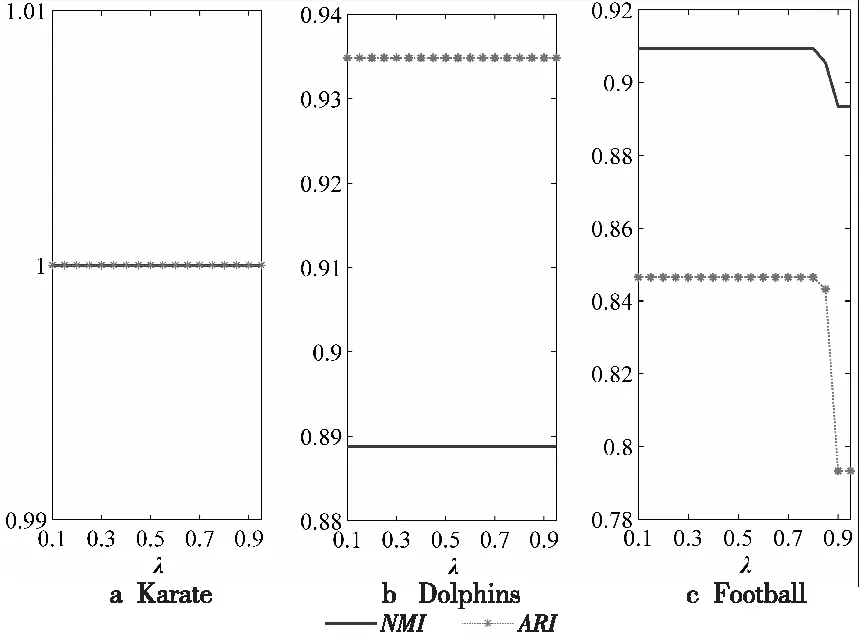
Figure 8 Parameter sensitivity (λ) of RLPBNI on real-world networks

在图8中，横轴为λ，以步长0.05从0.1递增到0.9，纵坐标代表NMI和ARI。由图8可知，在Karate和Dolphins网络上，λ的取值对NMI和ARI没有影响，其中在Karate网络上的NMI和ARI值均为1，划分结果与真实情况相符。在Football网络上，当λ≤0.7时，NMI和ARI值保持稳定；当λ>0.7时，NMI和ARI值开始逐步降低，说明在3个真实网络上，RLPBNI在λ≤0.7时效果最优。对于以上3个真实网络而言，对应的网络集聚系数分别是0.570 6，0.248 0和0.403 2，皆大于0.1，此时λ取较小值即可达到最优划分效果，因此最优λ可以取0.1或0.2。

Figure 9 Parameter sensitivity (λ) of RLPBNI on Net2 with different settings of μ

在图9的所有子图中，横轴为λ，且以0.1为步长由0.1递增到0.9，纵坐标表示NMI和ARI。9个子图中的K值为其对应网络的网络直径。可以看出，当μ≤0.2时，NIBLPA的精度与参数λ无关；当μ∈(0.2,0.7]时，算法精度随λ的增大而缓慢降低，且当μ=0.7时，算法精度随λ增大而降低的幅度降至最低；当μ∈[0.8,0.9]时，算法精度反而随λ增大而增加。这是因为随着网络混合系数的增大，网络中社区结构越来越不明显，需要对距离较近的节点分配较高的权重，以提高凝聚度，可使结果更为精确。而当社区结构较为明显时，为了充分辨识网络中节点影响力，距离较近的路径权重可设置较小，增大后期其他节点的参与度。社区网络结构的明显程度可以通过网络平均集聚系数反映，网络平均集聚系数与网络混合系数μ成反比。μ值越高，不同社团之间的辨识程度越差，节点之间的集聚效应越差，相对应的网络平均集聚系数越小。

由Net2网络所生成的9个衍生网络的网络混合系数和网络平均集聚系数如表3所示。显然，在表3中，Net2上的9个衍生网络的网络平均集聚系数都与网络混合系数μ成反比。结合图9和表3可以发现，当网络混合系数μ≤0.7时(即网络平均集聚系数≥0.04时)，λ的取值越小，RLPBNI的划分结果对应的NMI和ARI值越大，此时最优λ可取[0.1,0.3]；当网络混合系数μ>0.7时(即网络平均集聚系数<0.04时)，λ取值越大，算法划分效果则越好，此时最优λ可取0.9。上述分析进一步印证了RLPBNI的精度与参数λ及社区网络结构(平均集聚系数)之间的关系，并给出了不同情况下的最优λ取值。

Table 3 Average clustering coefficients on Net2 variants

5 结束语

本文提出基于节点影响力的理性节点标签传播算法RLPBNI，首次提出理性节点概念，通过节点整体影响力主动选择邻近节点中对自身影响最大的节点的标签作为更新标签，得到初始候选社区。然后，根据社区重叠度对初始候选社区进行再融合，并得到最终社区划分结果。通过模块度、NMI和ARI指标，在3个真实网络和2个人工网络上的实验结果显示，本文提出RLPBNI相比其他4种主流算法的精度更高，且在混合程度较高的网络上精度较高。此外，本文还分析并讨论了参数K和λ对RLPBNI的影响：通常，K对应网络直径，λ则与网络平均聚类系数直接相关，当网络平均聚类系数较大时，λ值越小越好；当网络平均集聚系数较小时，λ值越大越好。

本文算法依然存在一些不足：(1)只考虑了网络的拓扑结构对社区形成的影响，没有讨论现实社区节点间相互聚合时所需考虑的多种影响因素，例如节点的固有属性(如特征、描述及偏好等)；(2)只研究了无向网络中的节点归属问题，没有考虑有向网络，也未考虑到节点可能存在归属重叠的情况。未来将在节点标签传播的基础上，引入边标签的更新规则，以提高算法稳定性，进一步提高算法在社区结构模糊的重叠网络中的识别能力。