微小孔超声电火花复合加工通孔变幅杆设计

王鹏翔，于大国，李梦龙，王健，孟相辉

1中北大学机械工程学院；2山西省深孔加工工程技术研究中心

1 引言

电火花加工(EDM)是使用高温火花放电烧蚀工件表面，进而蚀除工件表面多余结构的加工方式。其最大的特点是非接触加工，对工件刚度和刀具刚度没有过多要求，所以多用于难加工导电材料，并在微小深孔的制备上应用颇多。例如飞机涡轮叶片的材料通常为镍基单晶合金，技术人员在制备气膜冷却孔时经常使用电火花打孔[1]；发动机喷油嘴的材料为耐高温复合材料，一般也通过电火花加工方式制备[2]；电火花加工也同样适用于一些超硬材料，类似聚晶金刚石、立方氮化硼等[3]。电火花加工处理速度慢，加工效率低[4，5]，这是由于其加工过程中的加工间隙小、工作液流速不恰当等因素，导致蚀除废屑堆积在加工平台上产生一系列不良反应[6]。同时，不断放电也会使电极损耗，如果不能及时控制电极丝与工件之间的放电间隙，将会出现“熄火”现象，使机床停运，大幅降低生产效率。

一些学者研究发现，超声电火花复合加工可以优化上述问题。超声振动频率超过28kHz，若将此振动加载到电火花机床的电极丝上将会有以下显著优点：放电通道加速成形，拉弧放电频次降低[7]，放电频次大大增加，超声空化、泵吸、涡流效应促进蚀屑排出，以及促进间隙介质的消电离等[8，9]。而在整个超声系统中，超声变幅杆起扩大振幅、使电极或工件的振动频率达到超声振动的重要作用。

本设计应用场景为超声电火花复合加工中的微小孔制备，制备过程中有两个常见的问题：

(1)微细电极的制造与安装一直是电火花加工中的难点，一般的装夹方式是由电主轴端部导入导向器中固定，因此存在以下问题：电极丝与导向器之间的摩擦力是否会导致电极丝的挠曲变形[11]；若电极丝损耗严重需要更换，是否可以将安装误差及变形误差等保持在可控范围之内;在更精密的微小深孔制备中，二次装夹的电极丝是否可以保证与工作台的垂直度和回转主轴的同轴度。

(2)电极丝脉冲放电时的冷却液是由非轴线方向的喷嘴喷入间隙中，且为了便于废屑排出，通常会加大单位时间的液体流量，但此方式会使电极受力不匀，导致电极偏斜或单侧电极损耗严重，并在单侧形成负压区域，影响放电状态；是否会导致积屑单侧堆积[12，13]。

基于以上问题，本文设计了一种轴线方向通孔的变幅杆结构，且在变幅杆两端分别添加了两个螺柱。此结构对电极丝有良好的导向固定作用，且可以由超声系统的轴线方向通入冷却液，防止外载冷却液的喷射对加工状态产生不利影响。

2 变幅杆设计

微小孔加工后的圆度和精度非常重要。若变幅杆的放大倍数增加不当，将会导致电极振幅过大，进而导致加工孔径变大[14]。因此需选择合适的放大倍数以及形状因数大、弯曲劲度大且更易加工的变幅杆。结合实际应用场景，分析谐振频率下的运动状态得出以下结论：

(1)不同材料的电极丝在同频率、单位时间内的损耗不同，但总体而言损耗不会太大，相比于变幅杆体积，该损耗微乎其微，所以可忽略电极丝的负载变化。

(2)采用电火花放电的方式加工微小孔无需接触工件，故不需要对电极丝施加静压力。

综上考虑，本文选择圆锥和悬链形变幅杆作为主要研究对象。为了与换能器相配，谐振频率f设计为28kHz，大端直径D1为40mm，小端直径D2为16mm。材料选最常见的45钢(见表1)。

表1 45钢材料性能表

2.1 悬链线形

悬链线被认为是最稳定的曲线，但由于悬链线形变幅杆加工成本太高，母线方程为超越方程难计算，因此在其创新方面少有研究。图1为悬链线形变幅杆的结构。设计此变幅杆需计算面积系数、谐振长度及放大系数等指标。

图1 悬链线变幅杆结构

面积系数为

(1)

式中，D1，S1为变幅杆大端的直径和面积；D2，S2为小端的直径和面积。

波长为

(2)

谐振长度为

(3)

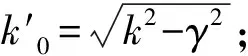
表2 两种变幅杆共振长度计算表

(4)

放大系数为

(5)

应变极大点可由超越方程算出

(6)

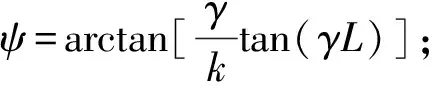
位移节点为

(7)

形状因数为

(8)

悬链线形变幅杆的母线变化由Dx=D2cosh[γ(L-x)]计算，如表3所示。

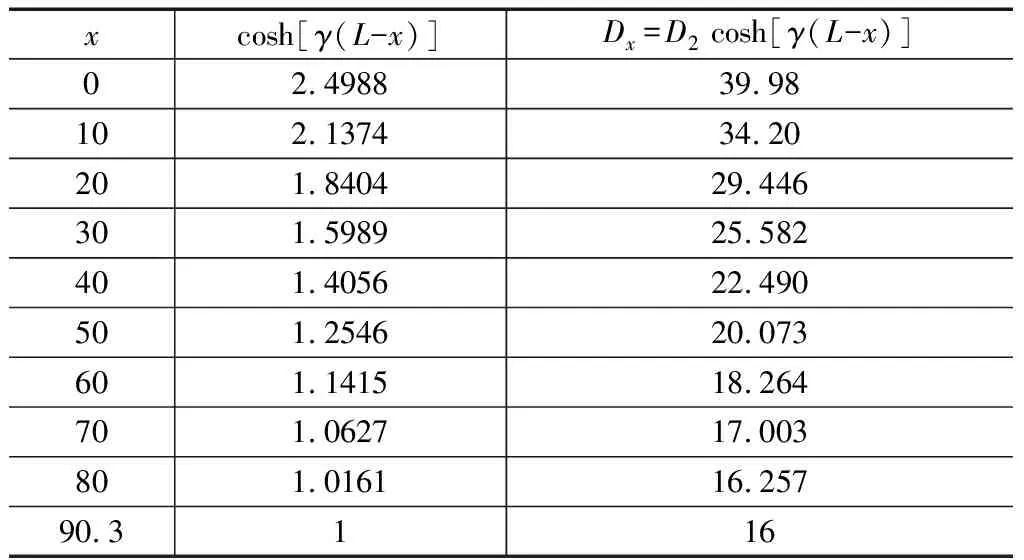
表3 悬链线形变幅杆尺寸

据上述计算，得出悬链形变幅杆的具体参数。其中谐振长度为90.33mm，放大系数约为2.503，节点位置在距离变幅杆大端36.73mm处。

2.2 圆锥形

圆锥形变幅杆是公认稳定性最强的单一形状变幅杆之一，形状因数大，设计成本低，但放大倍数相对最低。圆锥形变幅杆结构如图2所示。

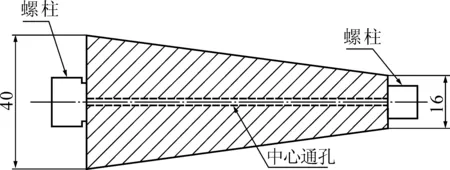
图2 圆锥形变幅杆结构

面积系数为

(9)

波长为

(10)

谐振长度为

(11)

圆锥形变幅杆的形状参数为

(12)

放大系数为

(13)

应变极大点可由超越方程算出

(14)

位移节点为

(15)

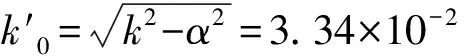
形状因数为

(16)

根据上述计算得，圆锥形变幅杆的谐振长度为99.44mm，放大倍数为2.45，节点位置在距离大端41.03mm处。

3 仿真及其优化

3.1 悬链形变幅杆仿真

将上文得到的数据导入SolidWorks软件中建模，完成后导入ANSYS软件中进行模态分析与谐响应分析。模态分析采用子空间的方法计算出20阶振型的谐振频率并选出最优解，然后根据最优频率进行谐响应分析，分析结果如图3所示。

图3 优化前仿真结果

通过分析结果可以发现，最优振型的频率为26.304kHz，仿真频率与设计频率相差1696Hz，计算得到优化前误差为6.05%。

其原因是：为了更贴近变幅杆的实际加工情景，夹紧中孔穿过的电极丝，所以在变幅杆两端分别添加了定位螺柱，导致仿真频率相差甚远。由于结果并不理想，故在此基础上对其进行了参数优化，同时由于仿真频率小于设计频率，故将变幅杆的谐振长度减小7mm，即将谐振长度由90.33mm减小到83.33mm后重新建模，求出距离变幅杆大端x处的截面直径Dx，其具体参数见表3。

表3 优化后悬链线形变幅杆尺寸

将重新建模后的变幅杆导入ANSYS软件进行分析，设置与前述相同。谐响应分析见图4。

图4 优化后仿真结果

通过分析优化后的模态发现，优化后的频率为28.41kHz，优化后误差为1.46%，符合初始设计频率。

由图4可知，大端输入一个3μm的振动位移，得到小端输出一个9.37μm的振动位移，此时的变幅杆放大倍数为3.12。与初始设计相比，悬链线形变幅杆放大振幅的能力得到优化。

3.2 圆锥形变幅杆仿真

将上文圆锥形变幅杆设计参数导入SolidWorks软件中建模，然后导入ANSYS软件中进行模态分析与谐响应分析。先划分网格，使用子空间分析方法得到该变幅杆20阶振型的谐振频率，并选择最优的谐振频率进行分析。分析结果如图5所示。

通过仿真分析发现，最优振型频率为26.652kHz，与设计频率相差1348Hz，优化前误差为4.81%。

这是由于伸入此变幅杆的电极丝需要夹紧，且在变幅杆两端添加了两个螺柱和一个轴向通心孔，导致频率误差较大。因此改变变幅杆长度使其达到目标谐振频率。经过不断缩减变幅杆长度，将预先设计的99.44mm谐振长度缩减至93.44mm并再次进行仿真，结果如图6所示。

图5 优化前仿真结果

图6 优化后仿真结果

通过优化后的模态分析发现，优化后的频率为28.213kHz，结合设计频率28kHz进行误差计算可以计算出优化后误差为0.76%。

由图6可知，大端输入3μm的振动位移，得到小端输出7.81μm的振动位移，此时变幅杆放大倍数为2.6，与初始设计相吻合，验证了设计频率和放大倍数。 计算后对两种变幅杆进行误差分析，结果见表4。

从表4可以得出以下结论：经过优化的悬链线形和圆锥形变幅杆的谐振频率十分接近，且优化后误差都很小。

4 实验验证

经过计算得知，两种变幅杆的谐振频率和放大倍数都达到了微小孔制备的标准。但最终选择了圆锥形变幅杆进行实物加工，具体原因如下：

(1)相同条件下，圆锥形变幅杆较悬链线形变幅杆的形状因数和弯曲劲度更大。

(2)所设计的变幅杆材料为45钢，该材料的损耗系数很高，所以尽量选用加工稳定性更高的圆锥形变幅杆。

(3)大振幅可能会扩大孔径，且设计的圆锥形变幅杆放大倍数为2.6，已经达到微小孔制备要求。

(4)母线为复杂函数的变幅杆加工成本很高，而圆锥形变幅杆加工较之更简便。

根据优化后的设计数据加工如图7所示的圆锥形变幅杆实物。

图7 圆锥形变幅杆

将YP-3828-4BZ柱形换能器与设计的圆锥形变幅杆相连，并连接阻抗分析仪，验证该变幅杆的谐振频率(见图8)。阻抗分析结果见图9。

图8 实验分析

图9 实验结果

由实验结果可得，此变幅杆的谐振频率为28.3kHz，导纳圆圆度高，机械品质因数高，电声转化能力较强，证明了所设计的圆锥形变幅杆具有可行性，为其在超声电火花机床的应用提供了理论依据。

5 结语

本文研究了可应用于超声电火花机床的轴心通孔变幅杆，并通过解析计算得到两种变幅杆的理论参数，再使用ANSYS软件对其进行了有限元分析和参数优化，并加工出圆锥形变幅杆实物。通过比较两种变幅杆的仿真与阻抗实验结果，得到如下结论。

(1)将解析计算得到的变幅杆进行仿真，得到悬链线形变幅杆优化前后的频率误差分别为6.05%和1.46%；圆锥形变幅杆优化前后的频率误差分别为4.81%和0.76%。频率误差均优化至总频率的1.5%之内，达到了设计要求。

(2)通过理论计算和仿真优化，计算出了两种变幅杆的放大倍数分别为3.12和2.6。选择了与仿真结果相近的圆锥形变幅杆加工实物。

(3)将变幅杆实物与28kHz的换能器连接，进行了阻抗分析实验。实验结果显示：此次实验导纳圆圆度高，频率为28.3kHz，与设计频率及仿真频率相差甚小。验证了此变幅杆的性能，为更多类型的超声变幅杆设计提供了思路。

(4)该变幅杆可轴线通入冷却液，减弱了外载喷射冷却液对加工的影响；该变幅杆可固定于机床上，电极丝由中心孔穿入，伸入电主轴中夹紧，对定位精度有很大的提升。