高浓度混合骨料充填料浆管道输送特性试验研究
吴 凡 ,杨志强 ,2,高 谦
(1. 北京科技大学土木与资源工程学院, 北京 100083;2. 金川集团股份有限公司, 甘肃 金昌 737100)
充填采矿由于具有安全、高效、经济和环保等优点,被越来越多的矿业国家认可并应用[1-2]. 管道输送作为充填采矿的关键技术之一[3],国内外对管道输送的相关研究成果越来越多. Wang等[4]利用Fluent软件对深井煤矿膏体管道输送的水力损失与流动速度进行分析,发现水力损失小于重力产生的压力可满足料浆自流. 吴爱祥等[5]基于结构动力学理论,研究了膏体管道输送阻力与流速、管径及物料组成的变化规律. Bharathan等[6]研究了管道输送中料浆的压力损失与摩擦系数的关系. 刘志祥等[7]通过环管试验并结合Fluent软件分析得到高倍线强阻力管道输送系统的最佳技术参数. 董慧珍等[8]通过管道输送试验,对体积分数为80%和81%的充填料浆的压力损失进行了研究. Kumar等[9]认为通过合理改变颗粒级配可降低管输压降及比能耗. 吴迪等[10]针对固液两相流的充填料浆,分析了料浆管道输送的阻力损失和弯管部分的受力情况.
高浓度料浆由于具有不离析、不沉降、效率高和井下脱水少等优点,其管输特性是充填采矿的重要研究内容[11-12]. 以甘肃某镍矿为工程背景,目前以棒磨砂为主的充填骨料无法满足该矿充填需求,必须补充使用充足廉价的废石和石灰石粉. 因此,开展由废石、棒磨砂和石灰石粉为主的混合骨料高浓度充填料浆管道自流输送特征研究,对矿山充填更具有指导意义. 本文利用该矿充填系统进行工业试验,观测得到不同高浓度和不同混合骨料料浆的管道压力及流量,分析了管输阻力随流速、料浆浓度和石粉掺量的变化规律,提出管输阻力的数学模型,并利用流变试验结果和机理分析进行对比验证,为高浓度混合骨料充填料浆自流输送技术的进一步发展提供理论依据.
1 试 验
1.1 试验系统
以甘肃某镍矿为工程背景,该矿充填管网布置为:充填料从制浆站下料口出发,通过充填钻孔到达充填平硐,然后经露天老坑钻孔到达主充填道,经穿脉运输道进入采场充填;管输特性测试系统由1台电磁流量计与4台工业压力变送器组成,每隔10 min记录流量数据,同时记录对应流量下各变送器压力数值. 试验系统如图1所示.
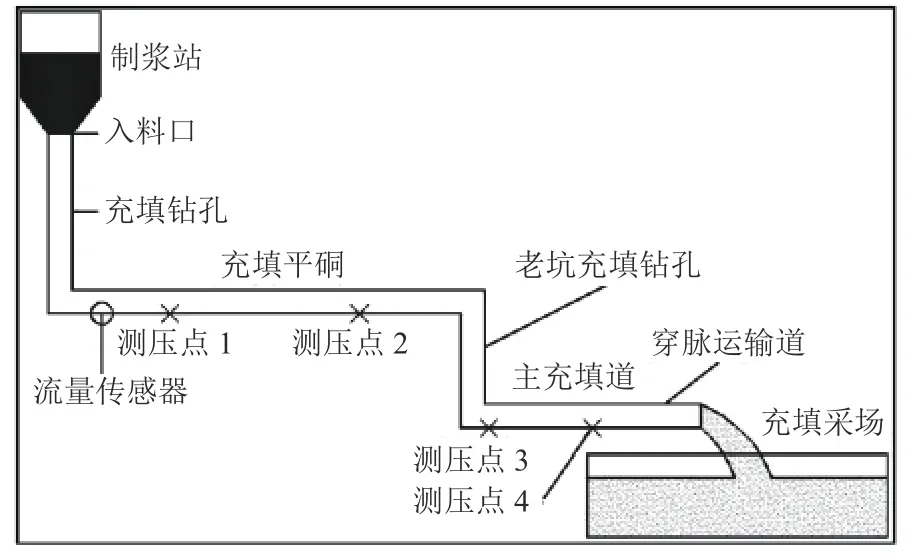
图1 管道输送试验系统Fig. 1 Experimental system of pipe transportation
1.2 试验材料
选用废石与棒磨砂作为粗骨料,石灰石粉(简称石粉)作为细骨料. 粗骨料中废石与棒磨砂质量比为3∶7,在粗骨料中添加石粉搅拌均匀制备为混合骨料,骨料级配曲线如图2所示. 胶结料为42.5水泥,充填所需水为工业用水.

图2 骨料级配曲线Fig. 2 Grading curves of aggregates
1.3 试验方案
高浓度料浆在静置沉降一段时间后仍能保持固液不分层状态,且当坍落度在230~275 mm内粗骨料充填料浆可自流输送[13-14]. 室内料浆沉降与坍落度试验结果表明:料浆在79%~82%浓度范围符合高浓度判定条件,并满足自流输送条件. 高浓度料浆添加细颗粒可提高浆体输送能力及降低能耗[15]. 室内强度配比试验结果表明:粗骨料中石粉掺量(c)超过40%时,充填体强度不满足矿山充填要求. 以料浆浓度与石粉掺量为影响因素,研究高浓度混合骨料充填料浆的管道输送特性,工业试验方案如表1所示.

表1 工业试验方案Tab. 1 Industrial test plans
2 结果与分析
2.1 管道压力变化规律
浆体管道输送压力试验研究的料浆浓度为80%、石粉掺量为20%(A2). 试验结果如图3所示.由图可知:管道压力随时间呈周期波动变化,随料浆输送距离增长呈减小趋势;测压点3压力波动变化幅度较其他测压点大,这是由于测压点3位于老坑充填钻孔与主充填道的弯管连接处,弯管处相对水平管压力变化大;测压点4的压力范围为0.11~0.22 MPa,与出料口形成压力梯度,料浆自流进入待充采场. 值得一提的是,引起管道压力波动变化的主要原因有3个:1) 充填骨料的差异性,在连续搅拌的不同时刻加入的骨料存在差异,其粒径级配并非完全相同,使得料浆密度、屈服应力、黏度等各个特性发生波动,进而导致压力波动;2) 充填料浆的非均质性,高浓度料浆可视为非均质流,无法达到理想均质状态,加之混合骨料中的最大颗粒粒径可达12 mm,料浆中大颗粒的不规则运动恰好经过压力传感器位置,可能引起压力波动;3) 充填系统配比波动,如料浆浓度为79%,由于充填系统自身特性使料浆浓度一般在78%~80%波动,连续充填造成测压点的压力波动是无法避免的.
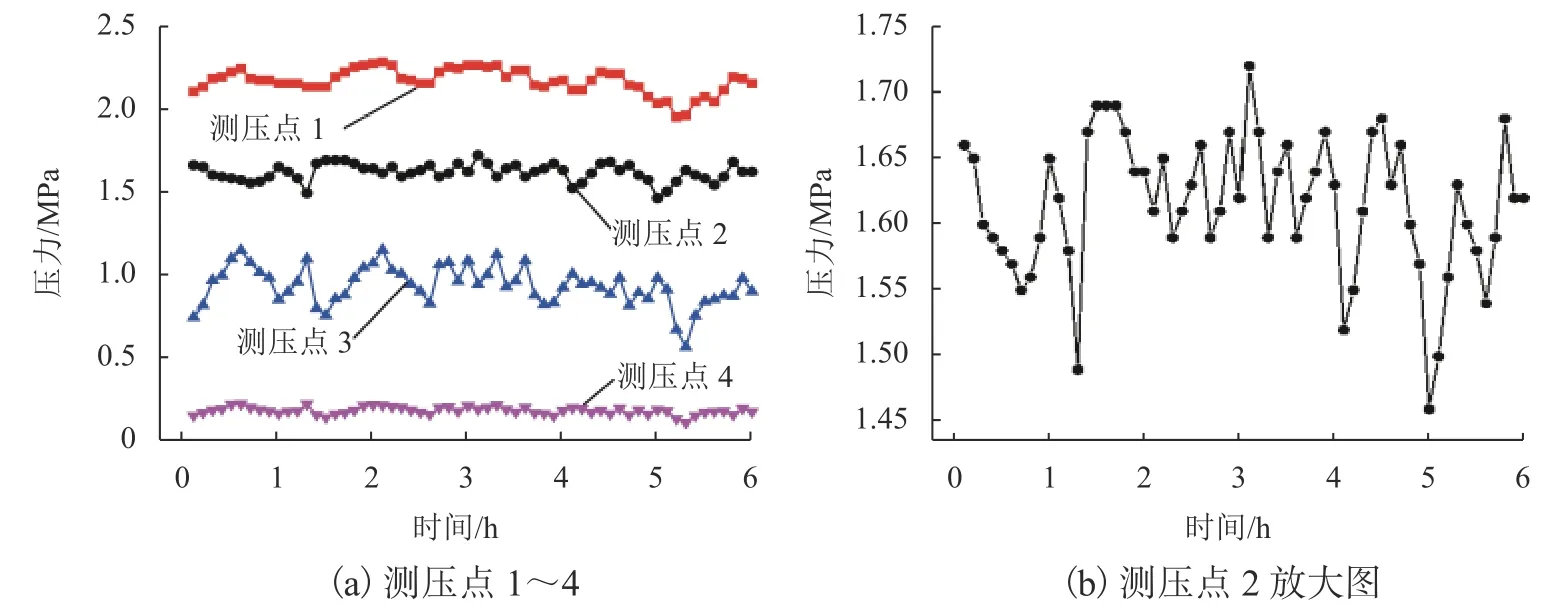
图3 压力变化曲线Fig. 3 Pressure variation curves
2.2 料浆浓度影响因素分析
为了研究管道输送阻力与料浆浓度的关系,工业试验采集了充填不同浓度料浆随时间变化的管道压力与流量,管道输送阻力(H,Pa/m)与管道压力及流速(v,m/s)与流量(Q,m3/h)的计算式[16-17]为
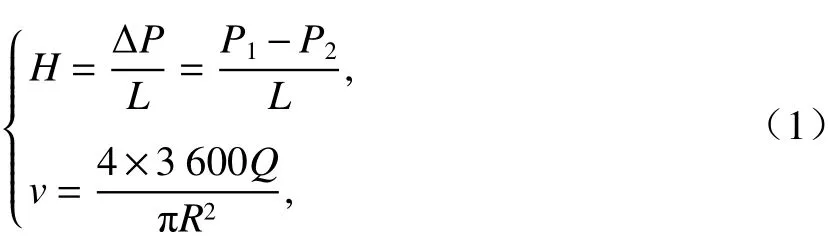
式中: ΔP为两测压点压力差,MPa;L为两测压点距离,m;P1和P2为测压点1、2的压力值,MPa;R为管道直径,m.
结合式(1)分析测压点1、2之间的管道输送特性,得到不同料浆浓度(cw)下管输阻力与流速的关系如图4所示.
由图4可见:在浓度一定时,随着流速的增加,不同浓度充填料浆管道输送阻力呈线性增长趋势,与环管试验[18]及数值模拟[19]的结论一致. 在流速一定时,管道输送阻力随料浆浓度变化而变化,浓度越高,阻力越大,与文献[8]结果类似. 对于不同浓度料浆,管道输送阻力与流速的回归直线几乎平行,说明在相同流速下,管输阻力与料浆浓度具有函数关系.在固定混合骨料时,管输阻力是料浆浓度与流速的二元函数,回归拟合得到式(2).

将不同浓度代入式(2)中,与图4中不同浓度料浆回归方程进行对比分析,最大相对误差为2.8%,平均相对误差为1.3%,模拟精度高.

图4 不同料浆浓度下管输阻力与流速的关系Fig. 4 Relationships between transport resistance and flow velocity of slurry pipes for different slurry concentrations
2.3 石粉掺量影响因素分析
为了研究管道输送阻力与石粉掺量的关系,按式(1)对工业试验中不同石粉掺量料浆的管道压力与流量作数据处理,得到不同石粉掺量料浆管输阻力与流速的关系如图5所示. 由图可知:在石粉掺量一定时,随着流速的增加,不同石粉掺量的充填料浆管道输送阻力呈线性增长趋势;在流速一定时,粗骨料未掺石粉时的管输阻力达到最大,粗骨料中石粉掺量达到30%时的管输阻力达到最小.

图5 不同石粉掺量料浆管输阻力与流速的关系Fig. 5 Relationships between transport resistance and flow velocity of slurry pipes for different stone powder contents
流速为3.2 m/s时管输阻力与石粉掺量的关系如图6所示. 由图可知:随着石粉掺量的增加,管输阻力先减小后增大. 在固定高浓度时,管输阻力是石粉掺量与流速的二元函数,回归得到式(3). 假设流速一定,由式(3)可知:管输阻力与石粉掺量符合抛物线变化规律.

图6 管输阻力与石粉掺量的关系Fig. 6 Relationship between pipeline transportation resistance and contents of stone powder

式中:分母中的20%为石粉中值掺量.
将不同掺量代入方程中,与图5中不同石粉掺量料浆回归方程进行对比分析,最大相对误差为2.5%,平均相对误差为0.8%,模拟效果理想.
2.4 管道输送阻力数学模型
不考虑料浆流速浓度与石粉掺量时,管道输送阻力随流速增大呈直线式增长,且料浆浓度与石粉掺量为相互独立的影响因素,由变量相互独立的性质有式(4)关系成立.

式中:H1(cw)为管道输送阻力与料浆浓度的幂函数关系(见式(2));H2(c)为管道输送阻力与石粉掺量的二项次函数关系(见式(3));H3(v)为管道输送阻力与料浆流速的线性函数关系.
式(2)是石粉掺量为20%时H1(cw)与H3(v)的乘积,式(3)是料浆浓度为80%时H2(c)与H3(v)的乘积. 不难发现,当料浆浓度为80%时的式(2)即为式(4)中的H3(v),由此得到高浓度混合骨料充填料浆管道输送阻力的数学模型:

为了进一步研究存在交互作用时三变量对管输阻力的影响规律,控制任意一个变量为固定值,利用Origin软件对数学模型进行可视化处理,如图7所示.
由图7可知:固定石粉掺量为20%时,料浆浓度与流速交互作用下管输阻力范围为2070~6920 Pa/m,管输阻力在料浆浓度与流速同时增大的作用下呈现增大的趋势;固定料浆浓度为80%时,石粉掺量与流速交互作用下管输阻力范围为2180~5970 Pa/m,管输阻力在石粉掺量减小及流速增大共同作用下呈现增大的趋势;固定流速为3.2 m/s时,石粉掺量与料浆浓度交互作用下管输阻力范围为3140~5530 Pa/m,管输阻力在石粉掺量减小及料浆浓度增大共同作用下呈现增大的趋势;不同交互作用下的管输阻力变化范围不同,由其区间大小得到交互作用对管输阻力影响程度从大到小依次为料浆浓度与流速、石粉掺量与流速、石粉掺量与料浆浓度.

图7 不同因素对管输阻力的交互作用Fig. 7 Interaction of different factors on pipeline transportation resistance
3 验证试验
为验证工业试验管输特性分析的准确性,在实验室内进行料浆流变试验,测试其流变特性参数.
3.1 不同质量浓度料浆流变结果与分析
选用R/S型软固体流变测试仪,并配备V40-20型浆式转子,测试石粉掺量为20%时不同质量浓度的料浆流变参数,试验结果如图8所示.
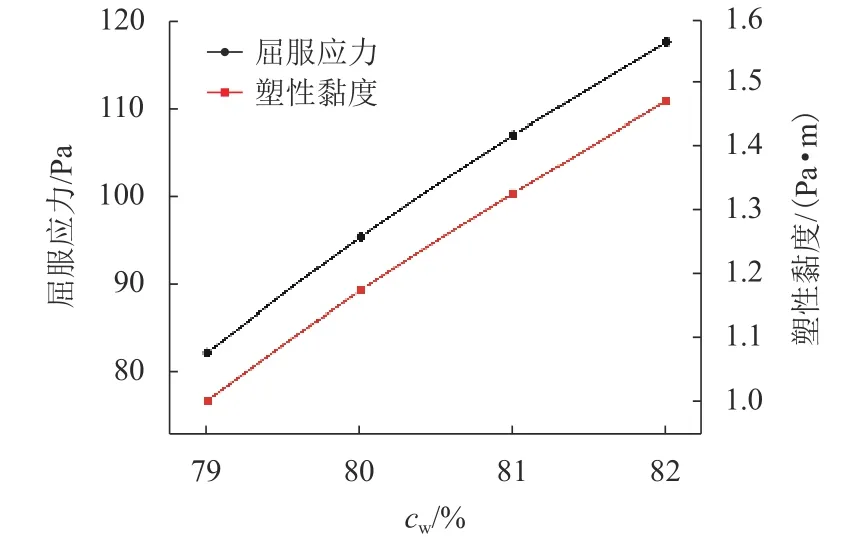
图8 不同质量浓度的料浆流变参数Fig. 8 Rheological parameters of slurry with different mass concentrations
由图8可知:在料浆浓度为80%时,料浆屈服应力的增幅达到最大为13.97 Pa,塑性黏度的增幅达到最大为0.17 Pa•m;随着料浆浓度的继续增加,增幅虽有所减小,但屈服应力与塑性黏度呈现继续增加的趋势,与料浆浓度对管输阻力的影响规律一致.
3.2 不同石粉掺量料浆流变结果与分析
在料浆浓度为80%时,对不同石粉掺量的料浆进行测试,其屈服应力及塑性黏度结果如图9所示.由图9可知:在石粉掺量为30%时,料浆屈服应力达到最小为87.74 Pa,塑性黏度达到最小为1.10 Pa•m;石粉掺量为40%时,屈服应力与掺量为20%时的屈服应力近似相等,塑性黏度略高于掺量为30%时的塑性黏度;随着石粉掺量的增加,料浆的屈服应力与塑性黏度均呈现先减小后增加的趋势,符合石粉掺量对管输阻力的影响规律.

图9 不同石粉掺量的料浆流变参数Fig. 9 Rheological parameters of slurry with different stone powder contents
4 机理研究
4.1 流速的振动效应
料浆在管道输送中,对于固定工况点,料浆流动速度随时间增长而有所不同,流速的改变引起的速度差会在浆体内固液(骨料(水泥)与水)分界处产生定向作用力. 这种定向作用力使保持平衡状态的介质质点产生机械振动. 料浆流速越大,介质质点的机械振动越强烈,增加了固体颗粒间的碰撞次数以使颗粒发生聚凝. 同时,粒的聚凝加强了不同分子及其介质之间的结合力,料浆的屈服应力与塑性黏度随之增加,导致了管输阻力的增加.
4.2 浓度的黏稠作用
当混合骨料中石粉掺量与料浆流速一定时,随着料浆浓度增加,直观表现为固体颗粒含量增加及水含量减少,微观表现为包裹固体颗粒的水膜变薄且数量减少. 水膜的变化加大了浆体的黏稠性,增加了屈服应力与塑性黏度,流变参数的增加导致了管输阻力的增加.
4.3 石粉的絮网理论
细颗粒在高浓度料浆管道输送中表现为絮网结构的作用[15],如图10所示. 由图可知:当高浓度料浆的质量浓度与流速一定时,随着石粉掺量增加,即浆体中的细颗粒所占比例增加,絮网结构发生改变. 结合图2可知:未掺石粉时,固体颗粒间隙较大,颗粒易发生碰撞,使颗粒发生聚凝;添加石粉后,细颗粒改变了骨料级配特性,并填充于粗颗粒间的空隙,颗粒间碰撞次数减少,颗粒间的聚凝变弱;当石粉掺量达到最优后继续添加石粉,多余细颗粒无法继续对空隙填充同时覆盖于浆体表面,增加了细颗粒与浆体间碰撞机会,聚凝效果增强. 不难发现,颗粒间的聚凝作用使不同分子及其介质之间的结合力先减弱后增强,改变了料浆的流变特性,从而产生管输阻力先减小后增大的现象.

图10 絮网结构变化示意Fig. 10 Schematic chart of flocculation network structure change
5 结 论
1) 通过工业试验,得到不同高浓度混合骨料充填料浆连续充填6 h的管道压力变化规律,管道压力随充填时间过程呈周期性波动变化,同时随输送距离变化呈减小趋势.
2) 基于管输阻力和流速的计算方法,得到管输阻力与流速、料浆浓度和石粉掺量分别呈线性、幂函数及抛物线关系.
3) 基于变量相互独立的性质,构建了高浓度混合骨料充填料浆的管输阻力数学模型,并从影响因素的相互作用分析发现,相互作用对管输阻力影响程度从大到小依次为料浆浓度与流速、石粉掺量与流速、石粉掺量与料浆浓度.
4) 结合验证试验,机理研究表明,流速的振动效应、浓度的黏稠作用与石粉的絮网理论是固体颗粒碰撞聚凝、颗粒水膜变薄减少和细颗粒填充粗颗粒间空隙等原因,导致料浆的屈服应力与塑性黏度也随之发生变化,从而改变了料浆的管输特性.

