基于轨道动检数据的轨道板的变形识别及预测

李晨钟 ，利 璐 ，汪健辉 ，冯晓云 ，王青元 ，黄传岳 ，王永华 ，何 庆

（1. 西南交通大学高速铁路线路工程教育部重点实验室, 四川 成都 610031；2. 西南交通大学电气工程学院, 四川成都 610031；3. 中国铁路上海局集团有限公司, 上海 200071）

板式无砟轨道能够为高速铁路提供较高的平顺性，是目前我国高速铁路线路中最主要的结构形式之一. 然而由于受到太阳辐射、路基沉降、轮轨动荷载等复杂因素的影响，轨道板在长期服役后容易出现板端翘曲、板中上拱变形等结构性病害[1-3]，使钢轨受迫产生挠曲变形，降低轨道平顺性，进而影响高速列车运行的安全性和平稳性. 此外，高速铁路覆盖范围广，里程沿线较长，采用人工检测轨道板变形病害的方法效率低下，且检测结果受限于工人的专业水平，难以实现稳定可靠的轨道板变形定位识别和变形劣化预测.

我国高速铁路板式无砟轨道按照型号具体可分为CRTS （China railway track system） Ⅰ、Ⅱ、Ⅲ型.目前，国内学者通过仿真分析对各类轨道板做了大量研究. 对CRTS Ⅰ型板的研究包括温度力作用下轨道板变形导致的层间离缝病害分析[4]；桥上Ⅰ型板结构变形与轨面几何不平顺的映射关系[5]等. 对CRTS Ⅱ型板的研究包括轨道板温度变形对钢轨的影响[6]，以及对车轨系统响应分析[7-8]等，研究表明，温度梯度是造成Ⅱ型板挠曲上拱的主要因素，受温度荷载影响，扣件支点反力与轮重减载率等各项动力学指标均明显增大. 对CRTS Ⅲ型板的研究包括温度及列车荷载作用下轨道板开裂、层间联结失效等结构病害的数值仿真分析[9]；高寒地区路基冻胀、融沉变形和不均匀沉降对轨道板变形、受力特性及车体动力响应分析[10]等. 然而以上研究大多基于数值仿真，侧重于分析轨道板病害发展的一般性规律，缺少相应的实测数据进行验证.

另一方面，国内外学者通过室外实验和道旁监测对轨道板变形进行了相关研究. 文献[11]对CRTSⅠ型轨道板做了室外实验，测试并分析了Ⅰ型轨道板温度梯度的统计特性，发现Ⅰ型板温度梯度沿板厚度方向具有明显的非线性；在水平方向，板端、板角、板中的温度变化幅度依次递减. 文献[12]提出了基于三轴加速度振动信号的轨道板监测系统，通过分析轨道板振动信号主频特性实现了异常轨道板识别. 文献[13]提出了基于光纤光栅技术的在线监测系统，实现了对轨道板横向变形的连续监测. 上述研究方法均采用对轨道板变形或振动的直接监测，属于“地对地”的监测方法，该类方法获取的数据质量较高，然而成本开销较大，且传感器长期曝露在外界环境下极容易受损甚至失效，难以适用于对广泛区间线路的长期监控.

随着高速铁路智能化运维需求的增长，及时、有效地掌握各部分轨道结构的信息是保障高速铁路安全运营的重要基础. 现有研究中基于物理模型的方法难以反映真实运营条件下的结构劣化规律，建立“地对地”的轨道监测系统则需要耗费大量成本，而我国目前普遍采用的轨道动检车能够对轨道平顺性进行定期、全覆盖的动态检测，属于“车对地”的检测方法. 轨道动态检测的方法成本较低，数据获取方式相对稳定，轨道动检数据在一定程度上反映了轨下结构的服役状态. 为此，作者对铺设CRTS Ⅰ、Ⅱ、Ⅲ 型3种轨道板的不同高速铁路线路长期检测的轨道动态不平顺进行数据挖掘，结合轨道高低不平顺时域，频域和空间域信息，得到温度荷载下高速铁路轨道板变形位置和劣化规律，为研究高速铁路轨道下部结构提供新的思路.

1 轨检数据介绍及预处理

轨道动态不平顺反映了轨道下部基础的结构变形，为了利用轨道动检数据分析温度荷载下轨道板变形，作者调研并搜集了2016年—2019年国内某3条高铁运营线路的轨道动检数据，其中包括了CRTS Ⅰ型板（40次检测样本，检测长度290 km），CRTS Ⅱ型板（74次检测样本，检测长度250 km），CRTS Ⅲ型板（100次检测样本，检测长度100 km）.轨检车的采样间隔为0.25 m，检测速度为300 km/h，记录的指标包括轨道高低（左右轨）、轨向（左右轨）、轨距、水平、三角坑等. 考虑到轨下结构及轨道板变形主要影响轨道高低变化，本文将采用左右高低不平顺作为研究轨道板变形的基础数据.

我国当前采用轨道动检车的里程标定系统基于GPS自动校正，该系统在检测过程中受到轮径尺寸误差、设备故障以及雨雪等恶劣环境影响，检测数据存在一定的里程误差[14]，且该误差随里程不断累积. 同时，在重新标定里程的过程中会出现里程重复和缺失等现象. 为此，利用文献[15]中提出的里程误差修正算法对原始数据进行了预处理，从而保证了数据的准确性和合理性.

2 轨道板变形评价方法

原始轨道高低不平顺数据可以看作随里程变化的时域信号，在不同里程位置，随着轨道板变形程度的不同，对应的高低不平顺幅值也有所变化. 然而，轨道板作为一种连续铺设的结构，由轨道板变形导致的轨道几何形位变化在高低不平顺中大致呈现出以轨道板纵向尺寸为波长的周期性，即高低不平顺特征波长[16]. 因此，需要在频域上考虑结构变形对高低不平顺特征波长的影响范围. 为了对轨道板变形程度进行量化分析，提出了小波能量的评价标准.

2.1 小波能量指标

小波能量的计算基于连续小波变换，其本质是一种常见的时频分析方法. 通过将拉伸或压缩后的小波函数与原始信号进行卷积运算，得到原始信号在各尺度下的小波系数，即代表了不同频率成分的显著程度. 由于小波系数为复数，对其取平方可以得到小波能量. 连续小波变换弥补了短时傅里叶变换中窗长固定的缺陷，使时频分析结果在低频部分具有较高的频率分辨率，在高频部分具有较高的时间分辨率，能够有效地运用于非平稳时间序列的研究，因此被誉为“数学显微镜”，在各领域的学术研究中得到了广泛运用[17]. 小波系数及小波能量的计算见式（1）～（2）.

式中：Wn(a,b) 为小波系数；a和b分别为尺度因子和平移因子；f(t) 为原始时域信号，t为时间；ψ (•)为母小波；为归一化因子，从而确保小波与尺度因子相互独立[17]；E为小波能量.

一般情况下，对时间序列进行分析时希望得到平稳连续变化的小波振幅，通常将非正交的Morlet函数作为母小波[18]. 如式（3）所示，该小波函数为一个对数衰减的复三角函数. 小波能量尺度与频率之间的换算见式（4）.

式 中：af为 尺 度 因 子；fs和fw分 别 为 采 样 频 率 和分析小波频率；wtar为目标波长；ω0为母小波中心频率[18].

考虑到轨道不平顺频域成分的复杂性，为了进一步分析轨道板变形引起的高低不平顺特征波长及其分布规律，根据常见轨道板结构尺寸，采用带通滤波器获取2～10 m波长范围内的高低不平顺波形.根据定义，相邻两个波峰或波谷之间的距离为一个波长. 根据波峰点位置计算高低不平顺滤波信号的波长（利用波谷点位置的计算结果类似），得到不同类型轨道板变形波长的频数分布直方图，如图1所示. 观察图1发现：不同类型轨道板的变形特征波长分布规律均近似符合拉普拉斯分布，图中黑色曲线即根据拉普拉斯分布拟合得到的概率密度曲线.

图1 不同轨道板的变形特征波长统计结果Fig. 1 Statistical results of deformation characteristic wavelength for different track slabs

拉普拉斯概率密度函数p(v) 和分布函数P(v)见式（5）～（6）.

式中：v为波长；µ为波长位置参数；λ为尺度参数，

为了方便后续讨论，将计算得到的加权小波能量定义为轨道不平顺劣化指标(track irregularity degradation index, TIDI)，其计算见式（7）.

式中：N为权重曲线长度；ωk为点k对应频率下的权值；Ek为点k对应频率下的小波能量值.

图2展示了Ⅰ型板对应的计算结果. 图上方的等值线热力图代表了特定波长和里程处的小波能量值大小，图下方的曲线为加权后的小波能量，即ETIDI. 从该计算结果可以看出：里程桩号K274 +500～K276 + 000区段内出现了两个尖峰值，能够较好地识别出4～10 m波长的小波能量异常位置.

图2 CRTS Ⅰ 型板部分区段计算结果Fig. 2 Calculation results of some sections of CRTS Ⅰ slab

2.2 评价指标合理性验证

将轨道高低不平顺的小波能量作为轨道板变形的评价指标是后续建模分析的基础，其合理性决定了识别和预测模型的准确度. 文献[19]通过功的互等定理建立温度荷载下弹性薄板的上拱模型，验证了在整体升温和温度梯度下轨道板上拱沿纵向呈正弦函数变化. 为了验证小波能量指标能够有效地反映轨道板变形，并考虑到实际变形曲线的复杂性，将轨道板变形曲线简化为沿纵向变化的正弦函数，并将跨中设置为变形异常区段，在此基础上利用德国低干扰谱的时域反演信号添加1～50 m波长的随机不平顺. 具体工况的设计见表1. 设计了700 m的随机不平顺，其中沿纵向里程方向有CRTSⅠ、Ⅱ、Ⅲ 型3种轨道板，每类轨道板20跨，不同轨道板之间间隔100 m. 叠加随机不平顺前，轨道板正常区段和变形异常区段的高程最大值分别设置为0.2 mm和0.6 mm.

表1 工况设置参数Tab. 1 Parameters of operation condition

图3为虚拟高低不平顺及对应的小波能量计算结果. 图3下半部分的曲线为高低波形，阴影部分为Ⅰ、Ⅱ、Ⅲ 型板对应的设置区段，深色阴影部分即跨中位置为变形异常区段；图3上半部分为小波能量计算结果，并用虚线框注释了不同类型轨道板对应的区段位置. 从该结果看出：小波能量异常位置和预先设置的工况基本吻合，对应的波长与结构长度也基本吻合. 验证了不同特征波长的轨道板在小波能量图中具有一定的区分度，利用小波能量作为评价指标能够有效地捕捉轨道板变形异常位置.

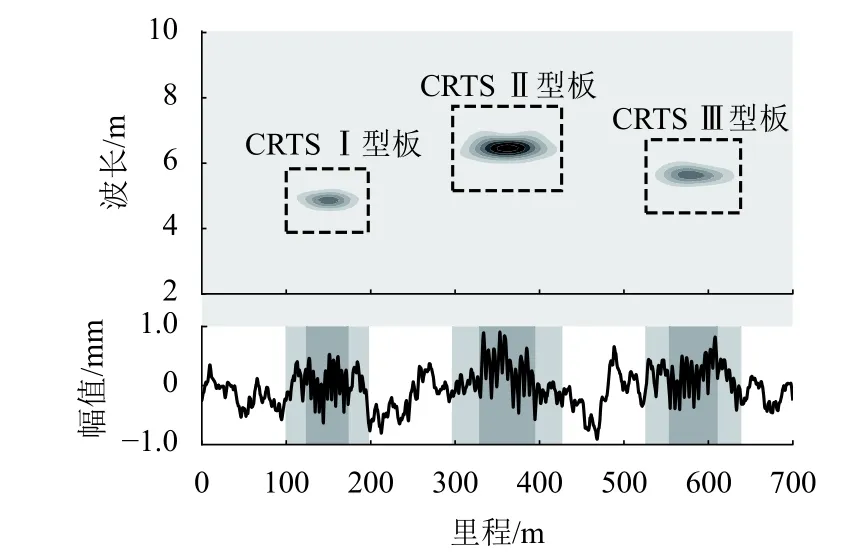
图3 虚拟高低不平顺识别结果Fig. 3 Identification results of virtual surface irregularity

3 轨道板变形时空数据分析

3.1 时空数据挖掘模型

由于检测设备和人为因素影响，动检数据往往具有一定程度的偶然误差. 为了避免误差对小波能量曲线的计算结果影响，对同一条线路的连续多次动检数据计算了小波能量曲线，从而得到了小波能量的时间-空间二维分布矩阵. 在空间尺度上，根据99.7%的置信度水平，小波能量值大于均值加3倍标准差的位置将被视为异常，基于此筛选标准可以得到若干疑似轨道板变形的里程坐标. 此外，由于轨道板变形异常位置的里程分布具有随机性，也没有任何先验分布的规律可循. 因此，引入了非参数的核密度估计方法对轨道板疑似变形位置进行统计分析，拟合得到TIDI异常值里程坐标的概率密度函数，从而得到最大概率发生轨道板变形的里程位置.

核密度估计的计算见式（8）.

式中：x为核函数输入；n为样本点数目；xj为样本点j处的输入；K(•)为核函数；h为核函数的带宽.

考虑到高斯分布良好的数学性质，本文在众多可选核函数中采用了高斯核函数[20].

确定轨道板变形的里程坐标后，结合小波能量时-空分布矩阵，可以提取变形位置处对应的小波能量值随时间的变化曲线，进而分析轨道板变形程度在时间尺度下的长期变化规律. 为此，采用了长短时记忆网络（long short-term memory network, LSTM）对小波能量时间序列进行研究. LSTM能够解决长序列数据在利用梯度下降法求解过程中出现的梯度消失问题[21]. 相较于一般的循环神经网络（recurrent neural network，RNN），LSTM的参数量更多，因此需要更多计算资源. 本文采用Python语言及Pytorch深度学习框架建立LSTM模型. 图4为LSTM神经网络的结构图，图中的大矩形框代表每一个神经元，该神经元能够对时刻t的输入xt做一系列变化得到当前预测输出，并且输出当前状态ct，当前隐变量ht到下一个神经元中，在xt+1中进行同样操作，反复多次后得到(i=1,2,···,T)，T为序列总时长.

图4 LSTM神经网络结构Fig. 4 Structure of LSTM neural network

LSTM模型中，z的作用是对当前输入xt和过去输出隐变量ht−1进行线性变换，得到新的当前信息.zi、zf和zo分别代表输入门、遗忘门和输出门，3个门操作分别决定了多大程度上输入当前信息，忘记过去的信息以及输出当前信息.z、zi、zf、zo的计算分别见式（9）～（12）.

式中：σ(•)为激活函数；W、Wi、Wc、Wo为权重；b、bi、bc、bo为偏置项，其值可以通过反向传播算法训练得到.

最终，当前状态量ct、当前隐变量ht以及当前预测输出值计算见式（13）～（15）[21].

3.2 不同类型轨道板变形预测结果

本文利用LSTM神经网络对轨道板变形异常位置处的TIDI时间序列进行了滚动预测. 为了方便后续讨论，将模型输入定义为历史数据，将模型输出定义为预测数据. 结果将对比不同历史数据时间长度和预测数据时间长度下的预测效果，历史数据时间长度和预测数据时间长度分别设置为15、30 d和45 d，按照不同的工况对测试序列进行预测，并将观测值和预测值之间的决定系数（R-square）作为预测结果的评价标准. 表2为不同测试工况下的预测Rsquare值. 该结果显示：当历史数据时间长度相同时，预测时间越长，预测效果越差；然而，对于同样的预测时间长度，增加历史数据时间长度并不能带来明显的预测效果提升. 这种现象可能是由模型过拟合造成的，因为更长的输入序列会增加更多的模型参数，而序列未来的数值往往只与序列最近的数值相关.

表2 不同轨道板预测结果的R-square值Tab. 2 R-square values of prediction results for different track slabs

图5（a）～（c）分别为3种轨道板的最佳滚动预测结果，阴影部分为检测当天最高、最低气温. 该结果表明轨道板变形程度随时间出现周期性变化，当地气温可能是其主要影响因素. 其中，Ⅰ、Ⅱ型板的变形程度与当地气温呈正相关，而Ⅲ型板变形程度与当地气温呈负相关，Ⅱ型板的变形程度较大，其残余变形随时间累积，到达一定程度后可能会导致轨道高低不平顺超限. 从TIDI的数值来看，Ⅰ、Ⅱ、Ⅲ 型板的TIDI数量级差距较大，其中Ⅰ型板最小，Ⅲ 型板次之，Ⅱ型板最大. 这与不同类型轨道板的结构和施工方式有关，Ⅰ型板为单元板，Ⅱ 型板为纵连板，而Ⅲ型板结合了Ⅰ型板的结构设计和Ⅱ型板的施工方式. 在温度荷载下，纵连板的内部应力相较单元板更大，因此更容易产生翘曲变形，而Ⅲ 型板介于两者之间，一定程度上缓解了纵连板的变形上拱，同时保证了线路基础具有较好的整体性.

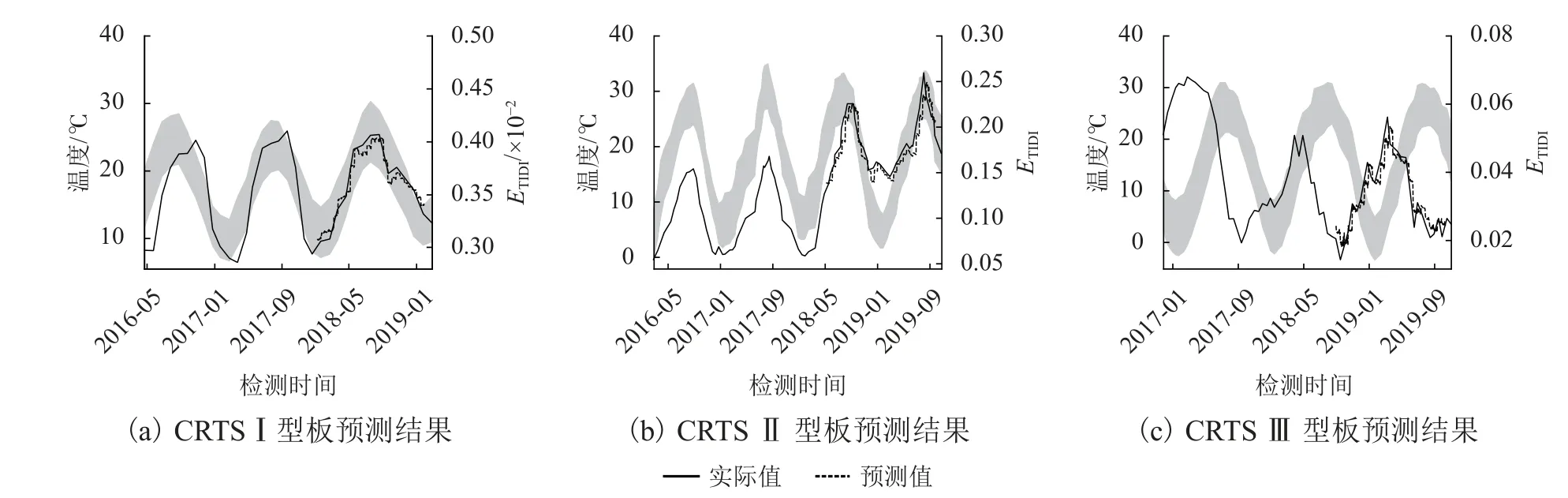
图5 不同轨道板变形预测结果Fig. 5 Deformation prediction results of different track slabs

3.3 轨道板变形温度特性分析

基于3.2节中各类轨道板变形的预测结果及变形程度与当地气温变化的相关性，为了进一步对比不同类型轨道板的温度特性，作者统计了大量区段的各类轨道板变形TIDI时间曲线和温度时间曲线的皮尔逊相关系数. 图6为不同类型轨道板的变形程度和当地气温的相关性分析的统计结果，不同线型的曲线代表了不同类型轨道板的变形程度与温度之间的相关系数的分布情况. 由相关系数的数学性质知道，轨道板变形程度和温度相关系数介于−1到1之间，且越靠近 −1说明轨道板变形程度在低温季节越显著，在高温季节减缓，反之亦然. 从图6中的统计结果可以看出：CRTS Ⅰ、Ⅱ型板，路基Ⅲ型板的变形程度与温度大多呈正相关，而桥上Ⅲ型板的变形程度与温度大多呈负相关.

图6 温度与各类轨道板变形相关性分析Fig. 6 Correlation analysis between temperature and deformation of different track slabs

此外，统计了桥上、路基CRTS Ⅰ、Ⅱ、Ⅲ 型板的TIDI值的分布规律，其结果如图7所示. 其中横轴代表不同类别的轨道板，纵轴为TIDI取对数值（为了避免各类之间TIDI值数量级上的差距）. 从图7可以看出：桥粱、路基Ⅰ型板的变形程度TIDI指标远小于Ⅱ、Ⅲ 型板的TIDI值，Ⅱ型板的TIDI值最大，由此推测Ⅱ型板在温度荷载下的变形程度最大，对轨道高低不平顺的影响最严重.

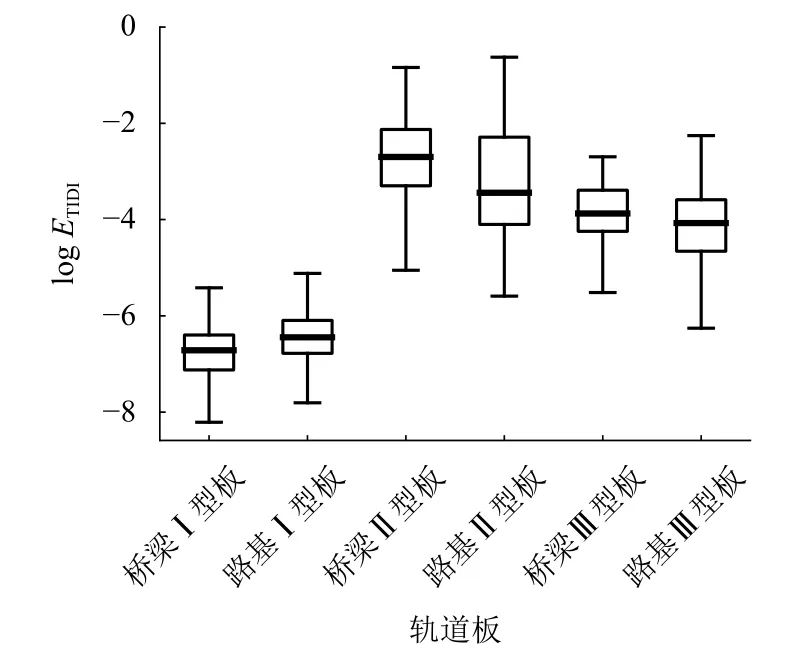
图7 不同轨道板TIDI对数值Fig. 7 Logarithmic values of TIDI for different track slabs

4 结 论

1） 轨道板变形程度随时间具有较明显的季节性规律. Ⅰ、Ⅱ型板在高温季节时，受内部温度应力影响可能出现翘曲或上拱现象，而Ⅲ型板在低温季节可能会出现冻胀现象，从而导致轨道板变形加剧.CRTSⅡ型板的变形程度随时间具有明显的整体增长趋势，可以推测Ⅱ型板的残余变形随服役时间不断累积，最终导致高低不平顺值幅值超限.

2） 利用LSTM神经网络对TIDI值进行滚动预测时，当历史数据的时间长度相同，预测效果随预测时间长度的增加而降低；然而，对于同样的预测时间长度，增加历史数据时间长度并不能带来明显的预测效果提升. Ⅰ型板变形的最佳预测结果Rsquare值接近0.90，而Ⅱ型板、Ⅲ型板变形的最佳预测R-square值均超过0.90，总体而言，LSTM能够基本实现对不同类型轨道板变形未来15～30 d的短中期预测.

3） 根据不同类型轨道板计算结果的统计表明，CRTS Ⅰ、Ⅱ型板，路基Ⅲ型板的变形程度与温度大多呈正相关，而桥上Ⅲ型板的变形程度与温度大多呈负相关，可能是由冬季低温冻胀所致. CRTSⅠ型板的变形程度远小于Ⅱ、Ⅲ型板，Ⅱ型板出现变形病害时的变形程度最大，对轨道高低不平顺的影响最严重.

在实际工程中，铁路工作人员需要对历史轨道动检数据建立数据库，利用本文提出的预测模型定期更新轨道板变形信息. 根据预测结果，针对出现较大预测值的季节开展重点检测，并对轨道板变形指标出现异常的里程进行优先排查. 相较于全线路、全天候的普查工作，本文提出方法可以更有针对性地指导铁路工作人员的检测和维修工作，相应提高铁路运营安全.

本文仅考虑及分析了温度和轨道板变形的关系，尽管文中提出的方法不能全面反映导致轨道板变形的所有因素，然而本研究从概率角度出发，采用的一系列统计分析方法能够在一定程度上减少错误判断. 在未来的研究中，将对轨道板变形进行跟踪测试，从而验证本文所提出方法的有效性，并给出TIDI建议管理阈值. 同时，如果有可能获取诸如路基沉降、层间离缝等数据，一项未来值得研究的课题是通过多源数据融合与特征表征分析，对轨道板变形做出更准确的预测.