“一带一路”沿线国家经济增长与碳排放的关系研究

张莉萍

(西安石油大学 经济管理学院，陕西 西安 710065)

0 引 言

气候变化是全人类当前面临的最大威胁之一，而提升碳排放绩效是治理全球气候变化最具成本效率的方式之一。世界银行数据表明：“一带一路”沿线国家经济增长持续呈现“高排放、高增长、高能耗”的特点。[1]6-19《2018年全球环境绩效指数报告》显示，虽然“一带一路”沿线国家的平均经济增长率高于世界平均水平，但其能源使用量、二氧化碳排放量均远超同期世界平均水平，沿线国家的二氧化碳排放量占到全球二氧化碳总排放量的二分之一。沿线国家发展进程中所遭遇的严峻资源环境问题，成为可持续发展的最大挑战。习近平总书记在第二届“一带一路”国际合作高峰论坛上提出，高质量共建“一带一路”将是未来合作的主线，这为高质量建设“一带一路”能源合作提供思路和要求，应以生态文明与绿色发展理念为指导，把发展绿色经济作为可持续发展的有效途径。2015年3月发布的《推动共建丝绸之路经济带和21世纪海上丝绸之路的愿景与行动》中明确指出：“投资建设中应充分考虑气候变化影响”。因此本文试图分析“一带一路”沿线各国的能源消费、碳排放量与经济增长之间的关系，以期丰富对环境与经济协调发展的理论探索，为我国同沿线各国的能源合作提供参考依据。

1 文献回顾

温室气体大量排放导致的全球气候变化和生态破坏对经济发展带来了巨大的挑战，成为各国经济社会可持续发展的阻力。英国著名反传统经济学家米香在1967年出版的《经济增长的代价》中，以社会福利的主要来源为研究视角，指出现阶段经济增长的代价是透支未来的环境资源。自此之后发达国家学者对经济增长与环境保护之间的关系展开了研究，对于生态环境和经济增长之间的矛盾，早期的理论研究分为两类，分别是以D·L·Meadows和Mishan为代表的悲观论和以Julian L Simon为代表的乐观论。而实证研究大都以Gossman提出的环境库兹涅茨曲线假设的适用性、存在性进行分析，并且以环境库兹涅茨曲线为基础，研究经济增长与保护生态环境之间的关系。

Kraft于1978年利用二变量模型最先提出美国的经济增长与能源消费之间有单向的因果关系，能源消费总量随着经济增长的增加而增加。1991年美国学者Grossman，Gene M等[2]223-250利用环境库兹涅茨曲线(EKC)提出发达国家经济增长和环境污染之间呈倒“U”型关系，环境质量伴随着经济增长的积累呈先恶化后改善的态势，并发现发达国家早期普遍选择了以牺牲生态和环境为代价推动经济发展。Holtz Eakin， Selden等[3]85-101对人均碳排放与人均经济增长之间的因果关系进行考察发现，碳排放与GDP之间存在倒“U”型关系；Martinez Z， Bengochea M等[4]121-126得出人均GDP与人均碳排放之间存在“N”型关系；而另外一些学者如Jie H ， Patrick R等[5]254-259发现人均碳排放与人均GDP之间并不存在规律性的相关关系。M A Cole,A J Rayner等[6]401-416利用面板数据对人均年收入与生态环境指标间的关系进行研究，发现不同的环境指标在不同地区与人均收入之间的关系不同，有效的环境库兹涅茨曲线只存在于部分地区。国内许多学者就环境库兹涅茨曲线在中国的适用性展开了论证研究。高宏霞、杨林等[7]52-57采用我国各省的面板数据，证实了废气与SO2的排放量的环境库兹涅茨曲线为倒“U”型，区域拐点的不同反映了我国区域发展的不平衡。赵娜娜、王志宝等[8]122-133以中国的能耗模式为出发点，利用差异化的能源库兹涅茨曲线研究能耗模式对经济发展的作用，结果表明由于国内地区发展的不平衡，部分省区环境库兹涅茨曲线存在明显偏差，但近50年来中国依然主要依靠能源消耗来推动经济发展。

2 研究设计

2.1 模型构建

指数分解分析方法(Index Decomposition Analysis,IDA)、IPAT模型、环境学习曲线、环境库兹涅茨曲线和差异化的近岸海域水环境库兹涅茨曲线等研究方法都可以用来反映经济增长与环境之间的关系。本文在研究碳排放与经济增长之间的关系时选取运用较多的环境库兹涅茨曲线。在国内外学者对环境库兹涅茨曲线的理论和实证研究过程中，产生了许多回归模型，其中三次多项式模型具有利于消除异方差性、形式灵活的特点，得到结果呈现多样性，既可以是倒“U”型、也可以是“N”型曲线，具有更好的拟合效果等优点。综上，本文选取三次多项式来研究“一带一路”沿线国家能源消费、能源强度、碳排放与经济增长之间的关系，见(1)式：

lnyi,t=β0+β1lnGDPi,t+β2ln2GDPi,t+β3ln3GDPi,t+φi,t

(1)

在(1)式中，lnyi,t表示第t年国家i的碳排放总量，能源消费的自然对数lnGDPi,t、ln2GDPi,t和ln3GDPi,t分别表示国家i第t年实际GDP总量的自然对数及其平方和三次方。β0、β1、β2、β3和φi,t分别为截距、三个待估参数和随机误差项。模型中的待估参数取值决定了曲线不同的形状，具体有7种情况，模型曲线见表1。

表1 模型曲线

2.2 变量选取与数据来源

时间序列模型、截面数据模型和面板数据模型都可用于环境库兹涅茨曲线实证分析。面板数据分析可以克服时间短和样本数据量少等问题，相比传统方法增加了自由度并且能完全修正普通最小二乘法的标准偏差。本文的研究对象为“一带一路”倡议下与我国积极发展经济合作伙伴关系、共同打造政治互信、经济融合、文化包容的利益共同体的沿线国家，鉴于数据的可获得性和完整性，选取其中的俄罗斯、巴基斯坦等62个国家1960—2018年的面板数据为研究对象。各指标原始数据来源为世界银行WGI指数数据库和全球碳计划(Global Carbon Project)。

考虑到不同国家的人口状况差异和能源消费差异，为全面体现经济增长与能源消费和碳排放之间的关系，选取能源消费总量、人均能源消费、能源强度、碳排放总量、人均碳排放、碳排放强度、GDP总量和人均GDP分析一带一路沿线国家经济增长与环境约束之间的发展态势。

3 实证分析

3.1 能源消费与经济增长的EKC检验结果

3.1.1 描述性统计分析

描述统计的结果表明，以变量lnery为例，平均值为7.297，其最小值和最大值分别为1.627和11.384，其标准差为1.463。可以看出本文研究的各个变量的分布不存在较为明显的异常值，所以可以进行进一步的分析，基于能源消费与经济增长的描述性统计分析见表2。

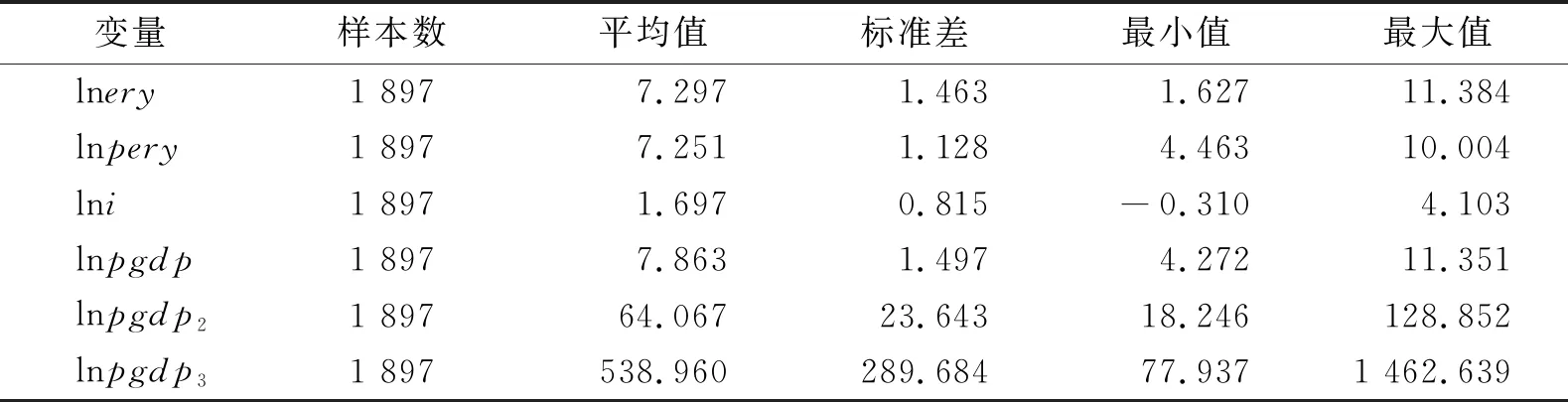
表2 基于能源消费与经济增长的描述性统计分析

3.1.2 单位根检验

当时间序列是非平稳状态时，在分析中容易出现“虚假回归”的问题。由此，为了保证分析数据的准确性，对本文的6个变量进行单位根检验，确定各个变量的平稳性。基于能源消费与经济增长的单位根检验见表3。

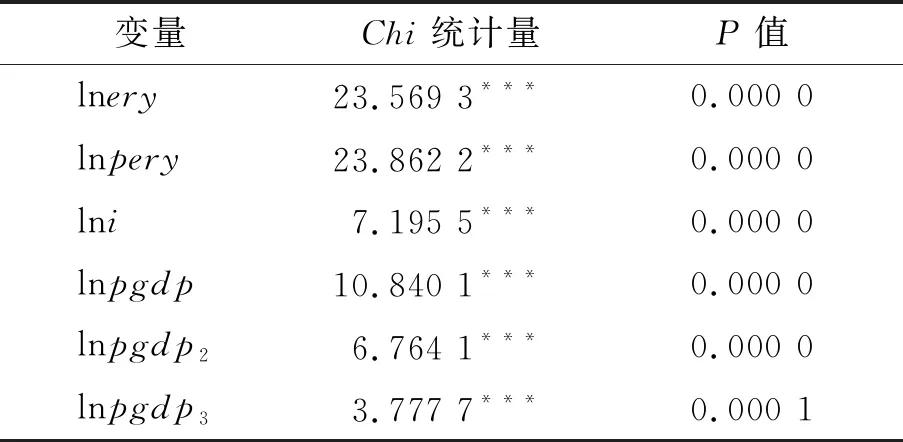
表3 基于能源消费与经济增长的单位根检验

根据表3的单位根检验结果，lnery、lnpery、lni、lnpgdp、lnpgdp2和lnpgdp3的Chi统计量为23.569 3、23.862 2、7.195 5、10.840 1、6.764 1和3.777 7，都通过了1%的显著性水平检验，表明各变量都拒绝了存在单位根的原假设，即各变量都是平稳的，可以进行后续的回归分析。

3.1.3 Hausman检验

为了确定模型选择结果，进行Hausman检验。在面板数据回归分析中，一般可以使用固定效应(FE)模型和随机效应(RE)模型，为了验证哪种模型更加适用，需要进行Hausman检验，基于能源消费总量的Hausman检验见表4。

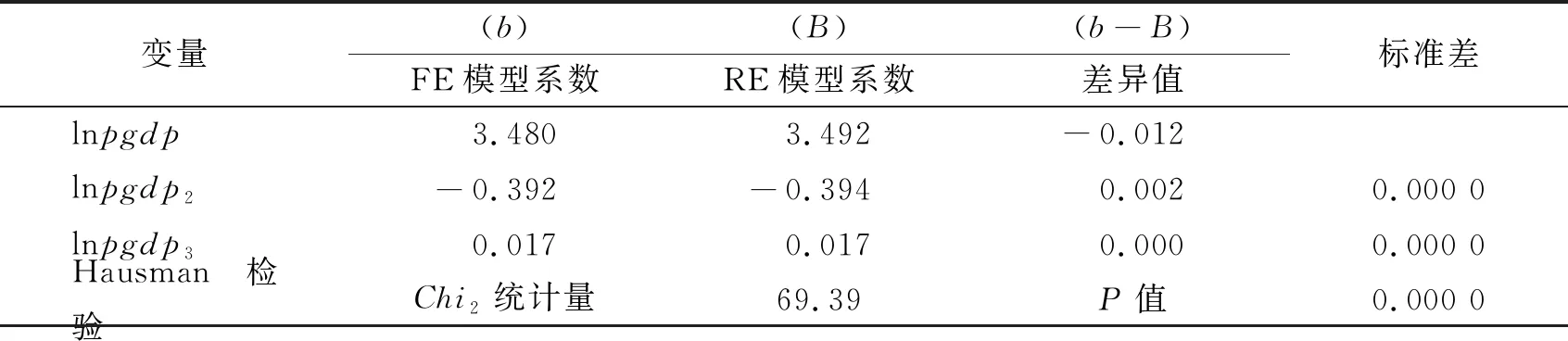
表4 基于能源消费总量的Hausman检验

根据表4中基于能源消费总量的Hausman检验，我们发现Chi2统计量为69.39，其P值为0.000 0，显著拒绝使用随机效应模型的原假设，所以hausman检验的结果表明应使用固定效应模型检验能源消费总量的EKC曲线。基于人均能源消费的Hausman检验见表5。

表5 基于人均能源消费的Hausman检验

根据表5中基于人均能源消费的Hausman检验，我们发现Chi2统计量为5.77，其P值为0.055 8，显著拒绝使用随机效应模型的原假设，所以Hausman检验的结果表明应该使用固定效应模型检验人均能源消费的EKC曲线。基于能源强度的Hausman检验见表6。

根据表6中基于能源强度的Hausman检验，我们发现Chi2统计量为5.77，其P值为0.055 8，显著拒绝使用随机效应模型的原假设，所以Hausman检验的结果表明应该使用固定效应模型检验能源强度的EKC曲线。

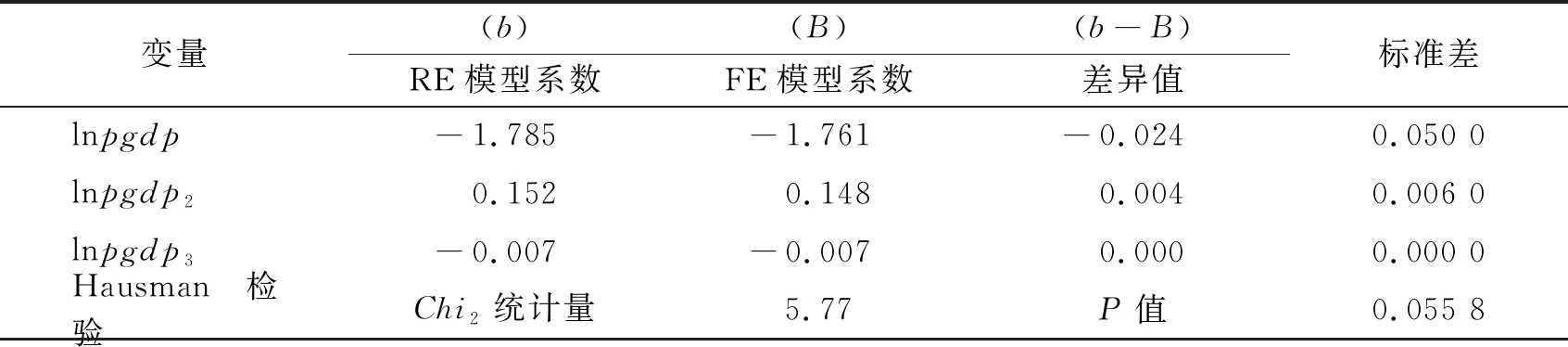
表6 基于能源强度的Hausman检验

3.1.4 基于面板回归的EKC检验结果

基于以上分析，我们需要使用固定效应模型对3个方程进行估计，以得到能源消费对经济增长的EKC检验结果、人均能源消费对经济增长的EKC检验结果和能源强度对经济增长的EKC检验结果。能源消费对经济增长的EKC检验结果见表7。

表7中的第(1)列报告了能源消费总量对经济增长的EKC检验结果，第(2)列报告了人均能源消费对经济增长的EKC检验结果，第(3)列报告了能源强度对经济增长的EKC检验结果。

表7 能源消费对经济增长的EKC检验结果

根据以上分析结果，我们发现第(1)列中经济增长一次项(lnpgdp)的系数为3.480，对应的t值为7.021，通过了1%的显著性水平检验。经济增长二次项(lnpgdp2)的系数为-0.392，对应的t值为-6.086，通过了1%的显著性水平检验。经济增长三次项(lnpgdp3)的系数为0.017，对应的t值为6.187，通过了1%的显著性水平检验。以上分析结果表明能源消费总量对经济增长的EKC曲线呈现出“N”型曲线的特征，即经济增长对能源消费总量的影响为促进-抑制-促进。

第(2)列中经济增长一次项(lnpgdp)的系数为-0.764，对应的t值为-2.390，通过了5%的显著性水平检验。经济增长二次项(lnpgdp2)的系数为0.148，对应的t值为3.566，通过了1%的显著性水平检验。经济增长三次项(lnpgdp3)的系数为-0.007，对应的t值为-3.706，通过了1%的显著性水平检验。以上分析结果表明人均能源消费与经济增长的EKC曲线呈现出倒“N”型曲线的特征，即经济增长对人均能源消费的影响为抑制-促进-抑制。

第(3)列中经济增长一次项(lnpgdp)的系数为-1.761，对应的t值为-5.511，通过了1%的显著性水平检验。经济增长二次项(lnpgdp2)的系数为0.148，对应的t值为3.553，通过了1%的显著性水平检验。经济增长三次项(lnpgdp3)的系数为-0.007，对应的t值为-3.690，通过了1%的显著性水平检验。以上分析结果表明能源强度与经济增长的EKC曲线呈现出倒“N”型曲线的特征，即经济增长对能源强度的影响为抑制-促进-抑制。

3.1.5 能源消费与经济增长的EKC曲线拐点计算

我们根据以上估计结果分别计算能源消费总量、人均能源消费和能源强度与经济增长的EKC曲线的拐点。首先，根据以上估计结果，能源消费总量、人均能源消费和能源强度与经济增长的EKC曲线方程见(2)至(4)式：

lnery=3.480lnpgdp-0.392(lnpgdp)2+0.017(lnpgdp)3-4.070

(2)

lnpery=-0.764lnpgdp+0.148(lnpgdp)2-0.007(lnpgdp)3+7.292

(3)

lni=-1.761lnpgdp+0.148(lnpgdp)2-0.007(lnpgdp)3+9.595

(4)

分别对上述方程求导可得(5)至(7)式：

(lnery)′=3.480-0.784lnpgdp+0.051(lnpgdp)2

(5)

(lnpery)′=-0.764+0.296lnpgdp-0.021(lnpgdp)2

(6)

(lni)′=-1.761+0.296lnpgdp-0.021(lnpgdp)2

(7)

因此，可得三个模型对应的拐点，能源消费与经济增长的EKC曲线拐点求解见表8。

根据表8分析，尽管能源消费总量与经济增长之间的“N”型曲线、人均能源消费与经济增长之间的倒“N”型曲线和能源强度与经济增长间的倒“N”型曲线均存在，但这种关系较为脆弱。其中能源消费总量和能源强度与经济增长的“N”型曲线和“N”倒型不存在拐点，由于能源消费总量方程的导数始终大于0，而能源强度方程的导数始终小于0，这表明随着经济增长的提升，能源消费总量会持续递增且能源强度会持续递减。对于人均能源消费来讲，当人均GDP低于340.76美元时，人均GDP提升会导致人均能源消费降低，当人均GDP在340.76美元与4 041.49美元之间时，人均GDP提升会导致人均能源消费提升，当人均GDP高于4 041.49美元时，人均GDP提升会导致人均能源消费降低。

表8 能源消费与经济增长的EKC曲线拐点求解

3.2 碳排放与经济增长的EKC检验结果

3.2.1 描述性统计分析

基于碳排放与经济增长的描述性统计分析见表9。

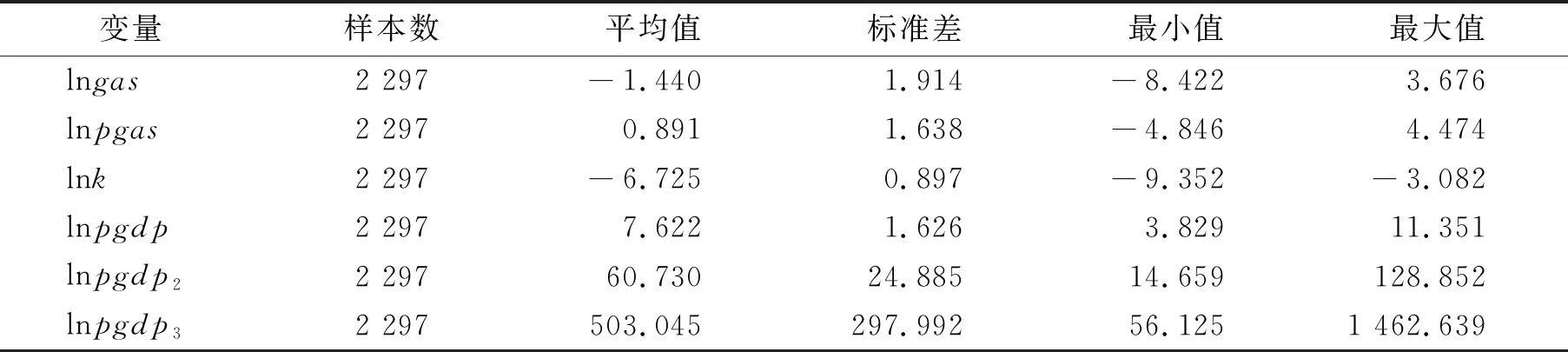
表9 基于碳排放与经济增长的描述性统计分析

由表9可知，描述统计的结果表明lngas的平均值为-1.440，其最小值和最大值分别为-8.422和3.676，其标准差为1.914。lnpgas的平均值为0.891，其最小值和最大值分别为-4.846和4.474，其标准差为1.638。lnk的平均值为-6.725，其最小值和最大值分别为-9.352和-3.082，其标准差为0.897。lnpgdp的平均值为7.622，其最小值和最大值分别为3.829和11.351，其标准差为4.373。lnpgdp2的平均值为60.730，其最小值和最大值分别为14.659和128.852，其标准差为24.885。lnpgdp3的平均值为503.045，其最小值和最大值分别为56.125和1 462.639，其标准差为297.992。可以看出本文研究的各个变量的分布都无较为明显的异常值，所以可以进行进一步分析。

3.2.2 单位根检验

众所周知，当时间序列是非平稳状态时，在分析中容易出现“虚假回归”的问题。由此，为了保证分析数据的准确性，对本文的6个变量进行单位根检验来确定各个变量的平稳性。基于碳排放与经济增长的单位根检验见表10。

根据表10的检验结果可知，lngas、lnpgas、lnk、lnpgdp、lnpgdp2和lnpgdp3的Chi统计量为21.687、23.492、13.274、11.709、8.225和5.783，都通过了1%的显著性水平检验，表明各变量都拒绝了存在单位根的原假设，即各变量都是平稳的，可以进行后续的回归分析。

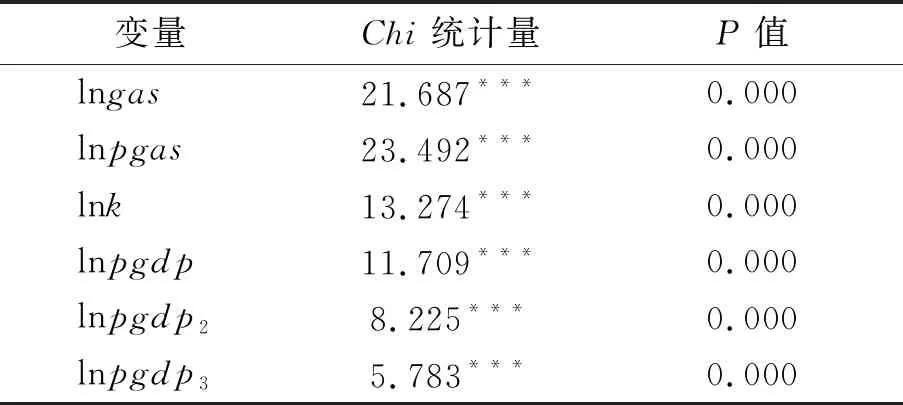
表10 基于碳排放与经济增长的单位根检验

3.2.3 Hausman检验

为了确定模型选择结果，本文进一步进行Hausman检验，Hausman检验是在一致性和有效性之间做一个权衡，在面板数据回归分析中，一般可以使用固定效应(FE)模型和随机效应(RE)模型，为了验证哪种模型更加适用，需要进行Hausman检验，基于碳排放总量的Hausman检验见表11。

表11 基于碳排放总量的Hausman检验

根据表11可知，Chi2统计量为5.14，其P值为0.161 8，没有显著拒绝使用随机效应模型的原假设，所以Hausman检验的结果表明应该使用随机效应模型检验碳排放总量的EKC曲线。基于人均碳排放的Hausman检验见表12。

表12 基于人均碳排放的Hausman检验

根据表12可知，Chi2统计量为93.84，其P值为0.055 8，显著拒绝使用随机效应模型的原假设，所以Hausman检验的结果表明应使用固定效应模型检验人均碳排放的EKC曲线。基于碳排放强度的Hausman检验见表13。

根据表13可知，Chi2统计量为94.58，其P值为0.000 0，显著拒绝使用随机效应模型的原假设，所以Hausman检验的结果表明应使用固定效应模型检验碳排放强度的EKC曲线。

表13 基于碳排放强度的Hausman检验

3.2.4 基于面板回归的EKC检验结果

基于以上分析，需要使用随机效应模型对(2)式进行估计，并使用固定效应对(3)式和(4)式进行估计，以得到碳排放对经济增长的EKC检验结果、人均碳排放对经济增长的EKC检验结果和碳排放强度对经济增长的EKC检验结果。碳排放对经济增长的EKC检验结果见表14。

表14中，第(1)列报告了碳排放对经济增长的EKC检验结果，第(2)列报告了人均碳排放对经济增长的EKC检验结果，第(3)列报告了碳排放强度对经济增长的EKC检验结果。

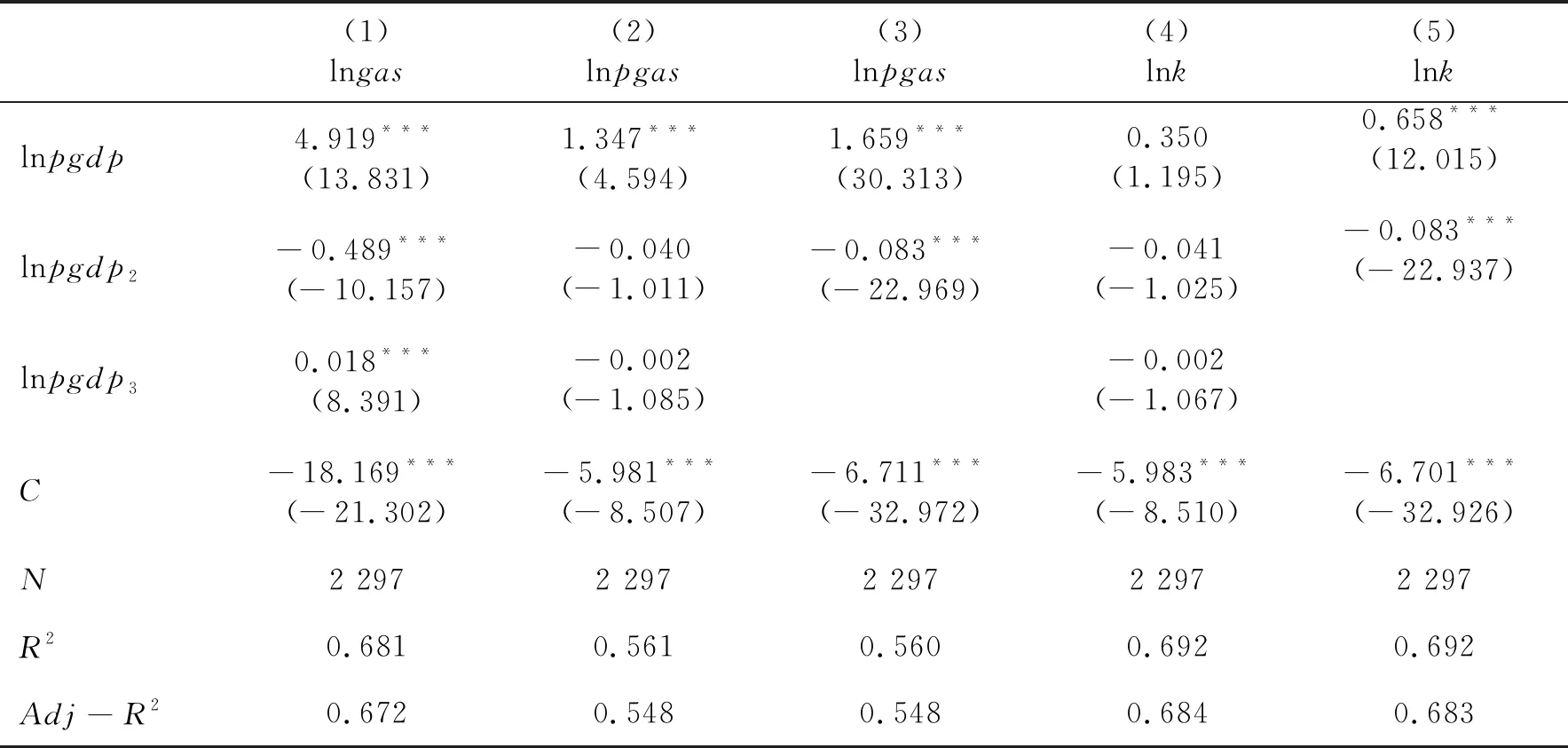
表14 碳排放对经济增长的EKC检验结果

根据以上分析结果，我们发现第(1)列中经济增长一次项(lnpgdp)的系数为4.919，对应的t值为13.831，通过了1%的显著性水平检验。经济增长二次项(lnpgdp2)的系数为-0.489，对应的t值为-10.157，通过了1%的显著性水平检验。经济增长三次项(lnpgdp3)的系数为0.018，对应的t值为8.391，通过了1%的显著性水平检验。以上分析结果表明碳排放总量对经济增长的EKC曲线呈现出“N”型曲线的特征，即经济增长对碳排放总量的影响为促进-抑制-促进。

第(2)列中经济增长一次项(lnpgdp)的系数为1.347，对应的t值为4.594，通过了1%的显著性水平检验。经济增长二次项(lnpgdp2)的系数为-0.040，对应的t值为-1.011，没有通过10%的显著性水平检验。经济增长三次项(lnpgdp3)的系数为-0.002，对应的t值为-1.085，没有通过10%的显著性水平检验。以上分析结果表明人均碳排放与经济增长的EKC曲线没有显著呈现出“N”型曲线的特征。我们去掉经济增长三次项进一步检验，其结果如第(3)列所示，其中经济增长一次项(lnpgdp)的系数为1.659，对应的t值为30.313，通过了1%的显著性水平检验。经济增长二次项(lnpgdp2)的系数为-0.083，对应的t值为-22.969，通过1%的显著性水平检验。这表明人均碳排放与经济增长的EKC曲线为显著的倒“U”型，即经济增长对人均碳排放的影响为促进-抑制。

第(4)列中经济增长一次项(lnpgdp)的系数为0.350，对应的t值为1.195，没有通过10%的显著性水平检验。经济增长二次项(lnpgdp2)的系数为-0.041，对应的t值为-1.025，没有通过10%的显著性水平检验。经济增长三次项(lnpgdp3)的系数为-0.002，对应的t值为-1.067，没有通过10%的显著性水平检验。以上分析结果表明碳排放强度与经济增长的EKC曲线没有显著呈现出“N”型曲线的特征。我们去掉经济增长三次项进一步检验，其结果如第(5)列所示，其中经济增长一次项(lnpgdp)的系数为0.658，对应的t值为12.015，通过了1%的显著性水平检验。经济增长二次项(lnpgdp2)的系数为-0.083，对应的t值为-22.937，通过1%的显著性水平检验。这表明碳排放强度与经济增长的EKC曲线为显著的倒“U”型，即经济增长对碳排放强度的影响为促进-抑制。

3.2.5 碳排放与经济增长的EKC曲线拐点计算

根据以上结果分别计算能源消费总量、人均能源消费和能源强度与经济增长的EKC曲线的拐点。能源消费总量、人均能源消费和能源强度与经济增长的EKC曲线方程见(8)至(10)式：

lngas=4.919lnpgdp-0.489(lnpgdp)2+0.018(lnpgdp)3-18.169

(8)

lnpgas=1.659lnpgdp-0.083(lnpgdp)2-6.711

(9)

lnk=0.658lnpgdp-0.083(lnpgdp)2-6.701

(10)

分别对上述方程求导可得(11)至(13式)：

(lngas)′=4.919-0.978lnpgdp+0.054(lnpgdp)2

(11)

(lnpgas)′=1.659-0.166lnpgdp

(12)

(lnk)′=0.658-0.166lnpgdp

(13)

求解二元一次方程，我们可得三个模型对应的拐点，碳排放与经济增长的EKC曲线拐点求解见表15。

由表15可知，尽管碳排放总量与经济增长之间的“N”型曲线，人均碳排放与经济增长之间的倒“U”型曲线，碳排放强度与经济增长间的倒“U”型曲线均存在，但这种关系较为脆弱。其中碳排放总量与经济增长的“N”型曲线不存在拐点，由于碳排放总量方程的导数始终大于0，碳排放总量会随着经济增长提升而持续递增。对于人均碳排放来讲，当人均GDP低于6 189.418美元时，人均GDP提升会导致人均碳排放增加，当人均GDP高于6 189.418美元时，人均GDP提升会导致人均碳排放降低。对于碳排放强度来讲，当人均GDP低于5 260.609美元时，人均GDP提升会导致碳排放强度增加，当人均GDP高于5 260.609美元时，人均GDP提升会导致碳排放强度降低。

表15 碳排放对经济增长的EKC曲线拐点求解

4 结论与建议

4.1 结论

(1)“一带一路”沿线国家经济增长与人均能源消费之间的关系图像呈倒“N”型曲线，沿线国家经济增长对能源消费的作用为抑制-促进-抑制。当人均GDP未达到340.76美元时经济增长对能源消费起到抑制作用，当人均GDP在340.76～4 041.49美元之间时经济增长对碳排放开始起到促进作用。

(2)“一带一路”沿线国家经济增长与人均碳排放的关系图像呈现倒“U”型曲线，沿线国家经济增长对人均碳排放的影响趋势为先促进、后抑制，当人均GDP高于6 89.418美元时，人均GDP提升会导致人均碳排放量降低。

对于大部分沿线的发展中国家来说亟需提高经济发展水平和发展速度，提高绿色发展意识，在经济发展达到一定的高度之后反作用于经济发展健康化、绿色化。近年来，虽然沿线各国家开始重视绿色全面协调可持续发展，在重视经济成绩的同时降低CO2排放量，使环境污染问题得到了缓解，大多诸如南亚和中南亚等地区的国家人口压力大、资源紧缺、整体能源利用率低和生态环境被破坏等将是一种长期的经济现象。要做到保护环境和发展经济并举，沿线国家中的大多数还需要经过经济发展和技术积累，并且坚持经济发展优先，在绿色低碳可持续发展方面还有很大的进步空间。

4.2 建议

根据上述结论，提出以下政策建议：

(1)沿线发展中国家需改变能耗模式、优化能源结构。“一带一路”沿线国家的发展水平差距较大，多数沿线国家经济发展水平和整体创新能力亟待提高，需要推进高效利用能源。通过加强与中国合作，积极向国际社会寻求帮助或者借助国际可再生能源署(IEA)开展国际合作，推动能源消费结构由化石燃料为主导的传统模式向风能、太阳能等清洁能源为主导的新型模式转换，推进经济系统绿色运行。

(2)推动绿色发展战略，制定产业结构转型升级政策，加大政府扶持力度。我国“十四五”规划和2035年远景目标纲要，专门用一个章节的篇幅论述如何推动共建“一带一路”沿线国家高质量发展，沿线国家必须将绿色发展战略与创新驱动战略深度融合，重视和有效利用“一带一路”的区域合作平台，促进自身国家的经济发展。建立良好的经济和政治制度，充分的产权保护，吸引外部投资与优秀的人才资源，提供更好的创新环境。

(3)可持续发展要求人与自然和谐共生、创造致力于实现绿色生活方式的政策和制度。在社会舆论道德约束的基础上，要求政府制定、修订和实施切实有力的生态环境保护管理法律法规，约束生产者和消费者的行为，加强基本环保知识的科普和媒体宣传力度，鼓励绿色技术创新，使节能贯穿始终，[9]34-42进而提高沿线发展中国家居民的环保意识与行为指数，促进实现可持续性发展的目标。

(责任编辑 王建卫)