新冠疫情下重庆市城市轨道交通运营风险评价

张尚毅，周米娜，郑先勇

(重庆交通大学 经济与管理学院，重庆 400074)

0 引 言

2020年1月，在我国发生了新型冠状病毒肺炎疫情(简称“新冠疫情”)公共卫生事件，为了切断疫情传播路径、控制人员流动，我国实施了“患者隔离”“人群分离”“减少接触”等应对措施，及时有效地防控了疫情，但也减少了人们出行频率，城市轨道交通客运量大幅度下降。根据《国家突发公共卫生事件应急预案》[1]，突发公共卫生事件可划分为特别重大、重大、较大和一般4级(表1)。可见，新冠疫情属于特别重大(I级)危害程度公共卫生事件，有必要开展其对城市轨道交通运营影响程度研究。

表1 公共卫生事件等级划分Table 1 Classification of public health events

国内外学者[2-4]分别运用模糊层次分析法、组合权重法和云模型对城市轨道交通运营风险进行了分析评估；黄宏伟等[5]分析了国内外地铁运营管理体系的异同点；叶庆辉等[6]利用综合性分析方法探讨了城市轨道交通运营风险；陈晓[7]运用系统动力学、杨兴宇[8]运用模糊ISM模型和FMICMAC模型、刘福泽等[9]运用结合TEI@I方法论的贝叶斯网络模型分别对城市轨道交通各方面运营风险进行了评估和分析；冯旭杰等[10]、付逸飞[11]分别从城市轨道运营方及公安机关的角度分析了新冠疫情的影响；曹磊等[12]对新冠疫情下城轨运营防疫提出了相关建议；徐建国等[13]针对突发事件提出了风险预警机制。

笔者以重庆市为例，开展了针对新冠疫情公共卫生事件下城市轨道交通运营风险的研究，通过构建的贝叶斯网络模型，对特大公共卫生事件下城市轨道交通运营风险进行了评估。研究结果可为城市轨道交通企业把握风险重点、风险程度，快速做出风险应对决策提供理论依据。

1 贝叶斯网络

贝叶斯网络适合分析具有不确定性的概率事件，可以在信息不充分、不确定的情况下对事件做出合理判断。贝叶斯网络的理论依据来自于贝叶斯公式(1)和全概率公式(2)：

(1)

(2)

式中：P(y|x)为事件x已经发生下事件y发生的概率，为后验概率；P(x|y)为似然概率；P(x)、P(y)分别为在完全不考虑其他因素情况下事件x、y发生的概率，为先验概率；i为事件个数。

贝叶斯网络由有向无环图和条件概率集构成，如图1，节点A、B为父节点，节点C为子节点，父节点与子节点之间用有向线段衔接。

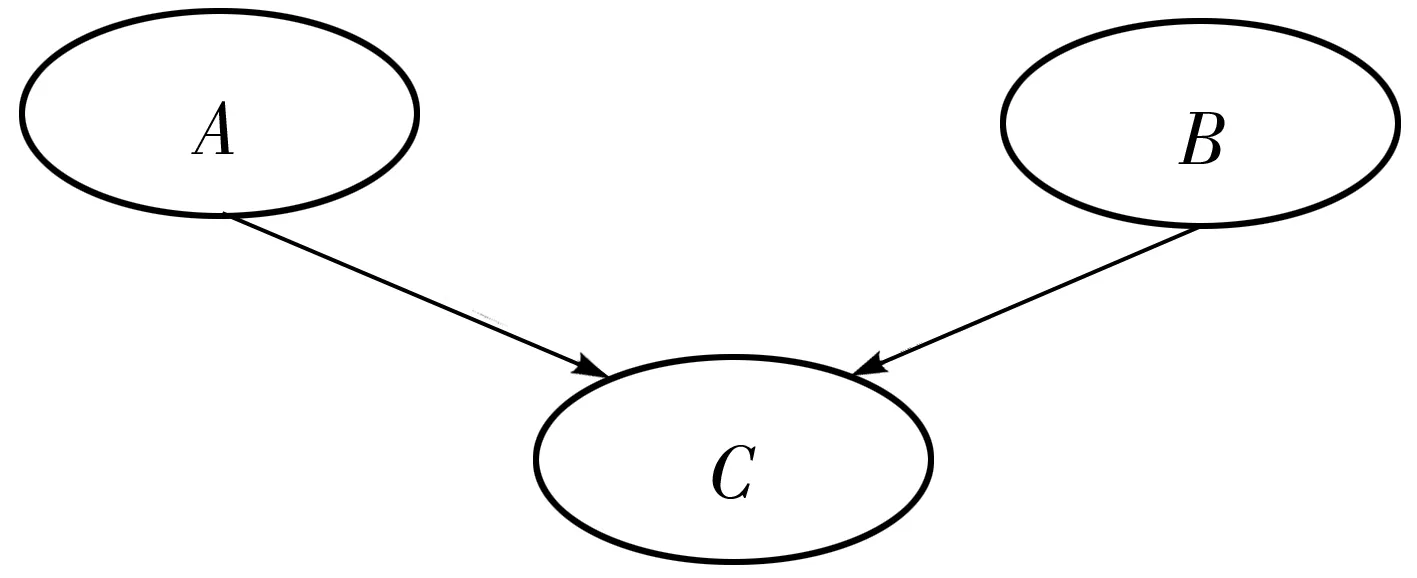
图1 贝叶斯网络示意Fig. 1 Schematic diagram of Bayesian network

可见，给定所有节点的先验概率及每个节点的概率集，即可得到包含所有节点的联合概率分布(3)：

P(A,B,C)=P(C|A,B)P(A,B)=

P(C|A,B)P(A)P(B)

(3)

式中：P(C|A,B)为节点A、B发生时节点C发生的条件概率；P(A)、P(B)分别为节点A、节点B发生的先验概率。

若一个复杂贝叶斯网络有节点V1,V2, …,Vn,且相互独立，则联合概率分解为式(4)：

P(V1,V2,…,Vn)=P(V1)P(V2|V1)…

P(Vn|V1,V2,…,Vn-1)

(4)

设π(Vi)为Vi父节点，则在条件独立的情况下，式(4)可简化为式(5)：

(5)

2 案例分析

2.1 模型构建

笔者运用Netica软件建模。假设同层内各因素间都是相互独立的，各层级风险因素的先验概率与条件概率主要通过专家打分、专家访谈等方式获得。

2.2 风险评价指标体系

在公共卫生事件背景下，城市轨道交通主要存在4大风险：经营风险Y1、应急管理风险Y2、乘客风险Y3及公共安全管理风险Y4，其下又包括12个指标。据此，构建城市轨道交通运营风险评价指标体系，见表2。

表2 城市轨道交通运营风险评价指标体系Table 2 Risk assessment index system of urban rail transit operation

图2为公共卫生事件下城市轨道交通运营风险指标和风险诱因贝叶斯网络拓扑图。图中：每个圆框中的状态表示该风险是否发生的先验概率；节点间带箭头的有向线段表示贝叶斯网络的构造关系。

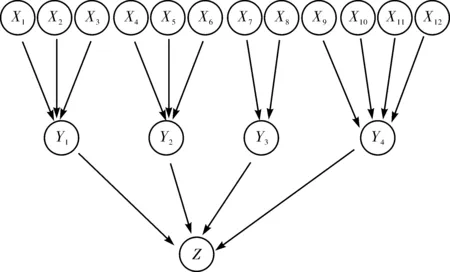
图2 贝叶斯网络拓扑图Fig. 2 Bayesian network topology

公共卫生事件下，4大风险Y1～Y4连接城市轨道交通运营总风险Z。总风险分高、中、低3级，分别表示影响与损失程度为较大、一般、较低。根据高、中、低风险概率分布，可判断风险等级以及所造成的损失程度。

2.3 模型计算与结果推理分析

2.3.1 子模型实例计算

1)邀请5位政府相关管理部门专家、15位轨道公司相关专家、15位高校专家共计35位专家填写问卷，收集节点的先验概率与条件概率，其中先验概率为新冠疫情中后期重庆市城市轨道交通运营现状的概率分布。

2)采用均值法对采集的数据进行处理，得到各节点条件概率分布。

由于节点较多，笔者仅截取经营风险子模型(图3)进行说明。

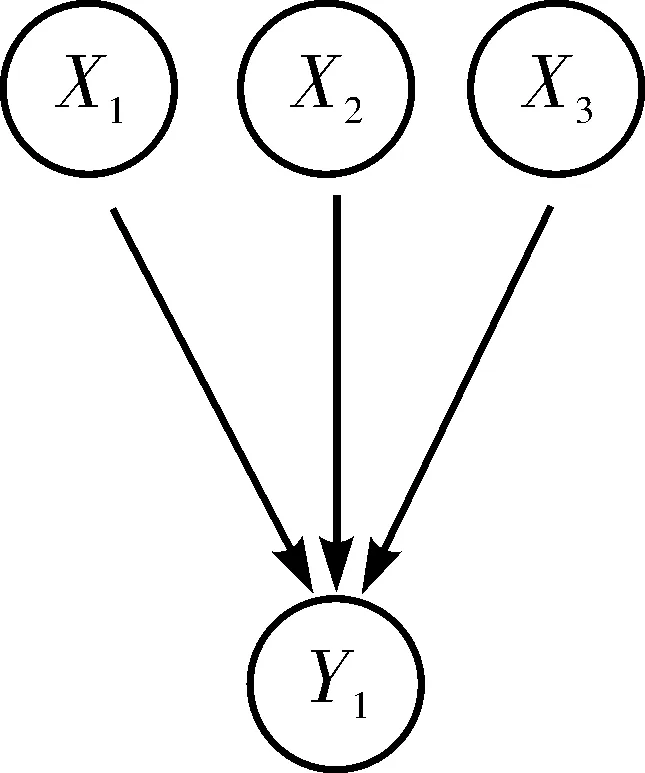
图3 经营风险子贝叶斯网络拓扑图Fig. 3 Topology of sub-Bayesian network of operation risk

经营风险的父节点的先验概率见表3，条件概率分布见表4。

表3 先验概率Table 3 Prior probability

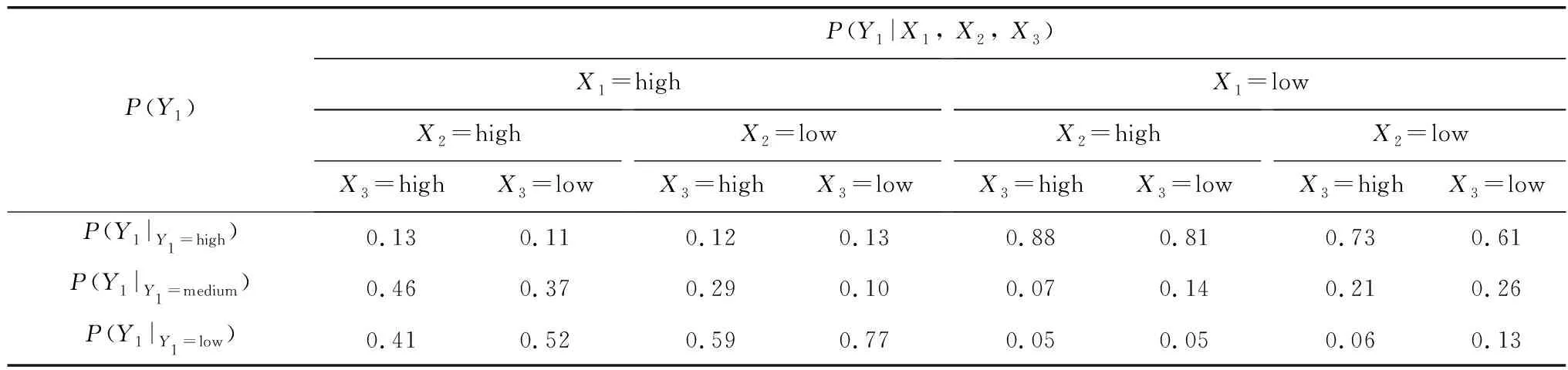
表4 条件概率Table 4 Conditional probability

表4的含义说明，以第1列数值为例，表示当客票收益高(X1=high)、采购防疫物资成本高(X2=high)、设备与人员防疫管理费用高(X3=high)时，经营风险处于高风险(Y1=high)的概率P(Y1|Y1=high) =0.13，处于中等风险的概率P(Y1|Y1=medium) =0.46，处于低风险的概率P(Y1|Y1=low) =0.41。

根据式(5)，结合表3先验概率和表4各节点条件概率，可计算得出案例中经营风险节点的概率分布：经营风险处于高风险的概率P(Y1|Y1=high) =0.239，处于中风险的概率P(Y1|Y1=medium) =0.344，处于低风险的概率P(Y1|Y1=low) =0.416。

运用Netica软件，输入各节点先验概率与条件概率，从而得到重庆市新冠疫情中后期城市轨道交通运营总风险概率分布，如图4。

2.3.2 风险节点状态正向推理

由图4可以看出，新冠疫情中后期重庆市城市轨道交通运营总风险处于高风险(Z=high)、中风险(Z=medium)、低风险(Z=low)的概率分别为P(Z|Z=high)=22.7%、P(Z|Z=medium)=39.4%、P(Z|Z=low)=37.9%。表明，新冠疫情中后期，疫情给重庆市城市轨道交通运营带来损失的程度为一般。

将先验概率调整为新冠疫情初期的状态，如图5。由图5可见：在新冠疫情初期，重庆市城市轨道交通运营总风险Z处于高、中、低风险的概率分别为P(Z|Z=high)=42.1%、P(Z|Z=medium)=37.1%、P(Z|Z=low)=20.8%。表明，新冠疫情初期，总风险Z为高风险的概率比中后期的大，为中、低风险的概率比中后期的低。说明新冠疫情初期给重庆市城市轨道交通带来的损失程度较高，这个结论与实际相吻合。

图4 新冠疫情中后期贝叶斯网络正向推理拓扑图概率结果Fig. 4 Probability results of forward inference topology of Bayesian network in the middle and later stage of COVID-19

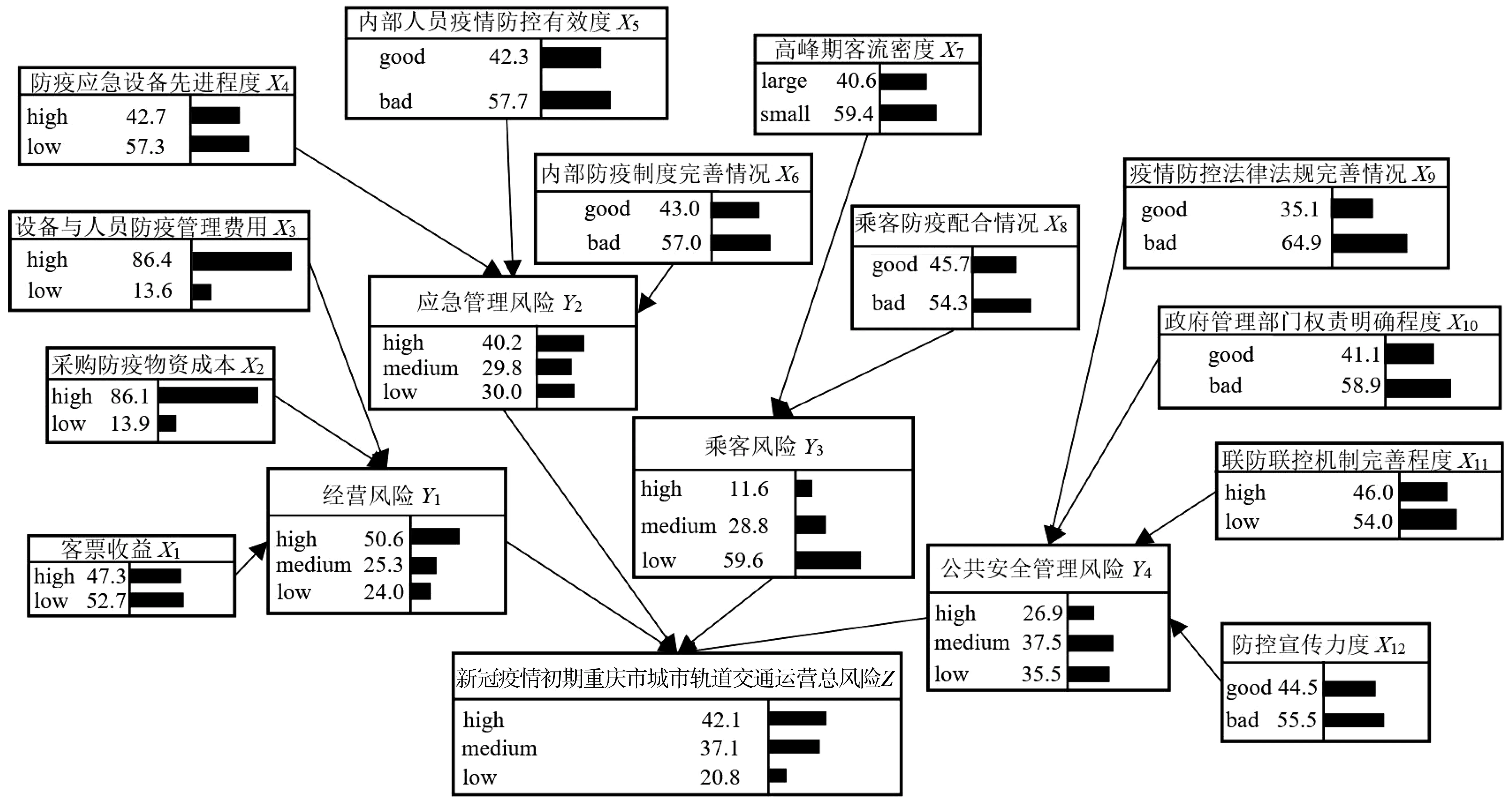
图5 新冠疫情初期贝叶斯网络正向推理拓扑图概率结果Fig. 5 Probability results of forward inference topology of Bayesian network in the early stage of COVID-19

2.3.3 风险节点状态逆向推理

贝叶斯网络还可以很方便地进行逆向推理。如果观察到公共卫生事件下城市轨道交通运营总风险概率状态的变化，则可以了解相关父节点的后验概率。

如图6，若新冠疫情下重庆市城市轨道交通运营总风险处于高风险的概率为P(Z|Z=high)=100%，则经营风险处于高风险的概率P(Y1|Y1=high) =55.9%，应急管理风险处于高风险的概率P(Y2|Y2=high) =28.2%，乘客风险处于高风险的概率P(Y3|Y3=high) =26%，公共安全管理风险处于高风险的概率P(Y4|Y4=high) =17%。可见，在新冠疫情下，当城市轨道交通运营总风险Z处于高风险的概率P(Z|Z=high)高时，经营风险、应急管理风险为主要风险。

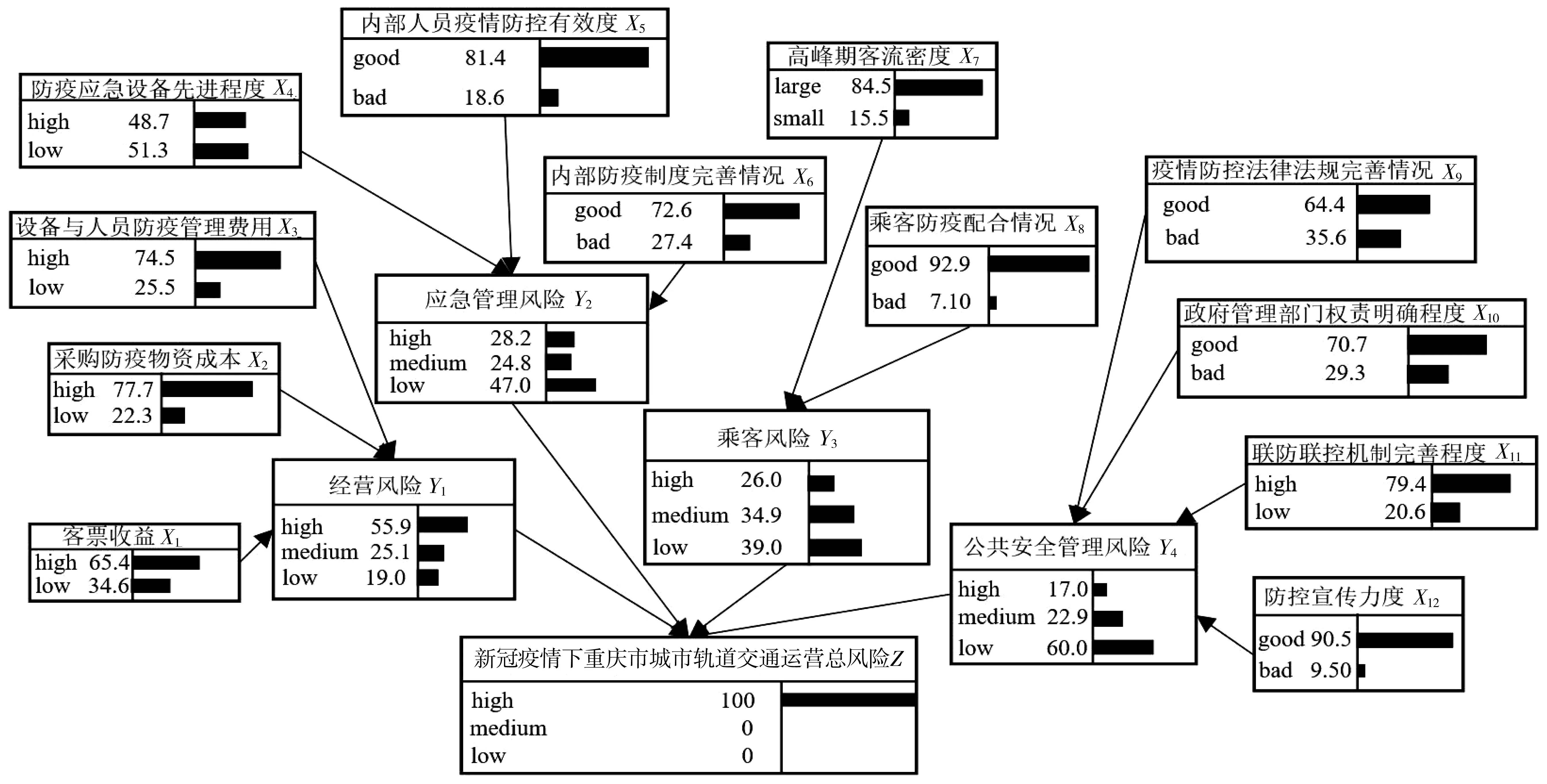
图6 贝叶斯网络风险节点状态逆向推理结果拓扑图Fig. 6 Topology of reverse inference results of risk node status in Bayesian network

可以通过分析各二级指标与一级指标的关联度来判断4大风险对运营总风险的影响程度。首先，确定自变量与因变量，设一级指标Z处于高风险的概率变化值ΔPZ为自变量，二级指标Y1、Y2、Y3、Y4处于高风险的概率变化值ΔPYi(i=1～4)为因变量，则逆向关联度ηYi为：

(6)

根据式(6)，当重庆市城市轨道交通运营总风险处于高风险的概率P(Z|Z=high) =0%→100%时，各二级指标的风险处于高风险的逆向关联度为：

可见，在新冠疫情下，4大风险对重庆市城市轨道交通运营总风险影响程度排序为：经营风险>应急管理风险>乘客风险>公共安全管理风险。

2.4 防控措施建议

2.4.1 优化城市轨道交通运营防疫效率

城市轨道交通企业应设置系统的内部人员健康监测管控机制和科学的防疫流程，以最短的防疫消毒时间和最合适的防疫费用实现高效防疫。在城市轨道交通运营前，对工作人员进行统一健康监测，落实防疫工作安排，明确防疫责任；在城市轨道交通运营中，保证列车与站台通风，及时清运站点与列车垃圾，定时为站点、列车进行防疫消毒；在城市轨道交通运营后，集中统一对站点、列车进行防疫消毒，监测内部人员健康情况，及时总结汇报当日防疫工作完成情况。

2.4.2 统筹调配应急物资

在应急物资体系上，依照重要商品储备机制，整合防控资源，建立轨道交通公共卫生事件防护物资的调配机制，设置应急物资储备与流动数据库；充分利用大数据，将防疫物资内容信息、防疫物资数量信息、防疫物资储备地点信息进行共享，打破部门行业单位的防疫物资信息流动传递壁垒，实时监控防疫物资储备与使用情况，以便在紧急时刻及时、有效地分配防疫物资资源。

2.4.3 完善乘客防疫机制

在公共卫生事件下，严格落实乘客乘坐城市轨道交通行为规范，如出示健康绿码、行程绿码、配合体温检测、全程佩戴口罩等。加强进站点对乘客健康状况的监测；加强列车行进过程中执勤人员对乘客防疫配合度的监督；加强出站口疏散工作，避免出站口乘客拥堵。在疫情严重时，充分运用网络及大数据功能，实时调取乘客防疫健康轨迹与健康状况，适时提前若干时间读取乘客相关健康数据，便于疫情追踪，迅速定位。

2.4.4 完善联防联控机制

统筹政府机构、公共卫生单位、企业、社区等各部门之间的联防联控机制；明确城市轨道交通企业防疫责任、防疫任务及防疫范围；加强各部门之间的沟通，优化各部门间信息网络共享机制，及时传递疫情信息，确保堵塞防疫漏洞。

3 结 语

当公共卫生事件发生时，城市轨道交通运营面临经营、应急管理、乘客及公共安全管理4大风险。以重庆市为例，构建了贝叶斯网络模型，分析并量化城市轨道交通运营在新冠疫情背景下面临的主要风险及风险程度。研究结果表明：在新冠疫情中后期，由新冠疫情引起的重庆市城市轨道交通运营总风险Z为一般风险；当总风险Z处于高风险的概率P(Z|Z=high)高时，经营风险、应急管理风险为主要风险；当P(Z|Z=high)=0%→100%时，经营风险对总风险Z影响最大。