基于NSGA-Ⅱ算法的并联机器人结构分析及优化

范浩东，王宗彦，宋灵芝，王 曦，张宇廷

(1.中北大学机械工程学院，山西 太原 030051)(2.山西省起重机数字化设计工程技术研究中心，山西 太原 030051)

工业机器人现被大规模应用于工业生产的各个领域，是实现智能制造的主要手段之一，可以让劳动者从乏味繁重的单一体力劳动中解脱出来，同时有效提高生产效率与质量。与互补型结构的串联机器人相比，并联机器人有着优异的重载比、更高的精度和刚度、更小的占空比以及更小的累计误差和惰性。目前，对多自由度DELTA并联机器人的研究已经较为深入，但是对少自由度机构的研究却不多。然而在日常生产生活中，较多的时候只需要机器人有较少的自由度就能完成任务，且少自由度机器人结构简单、成本低廉，因此具有实际的研究意义。

1 建模及工作空间分析

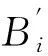
图1 并联机构

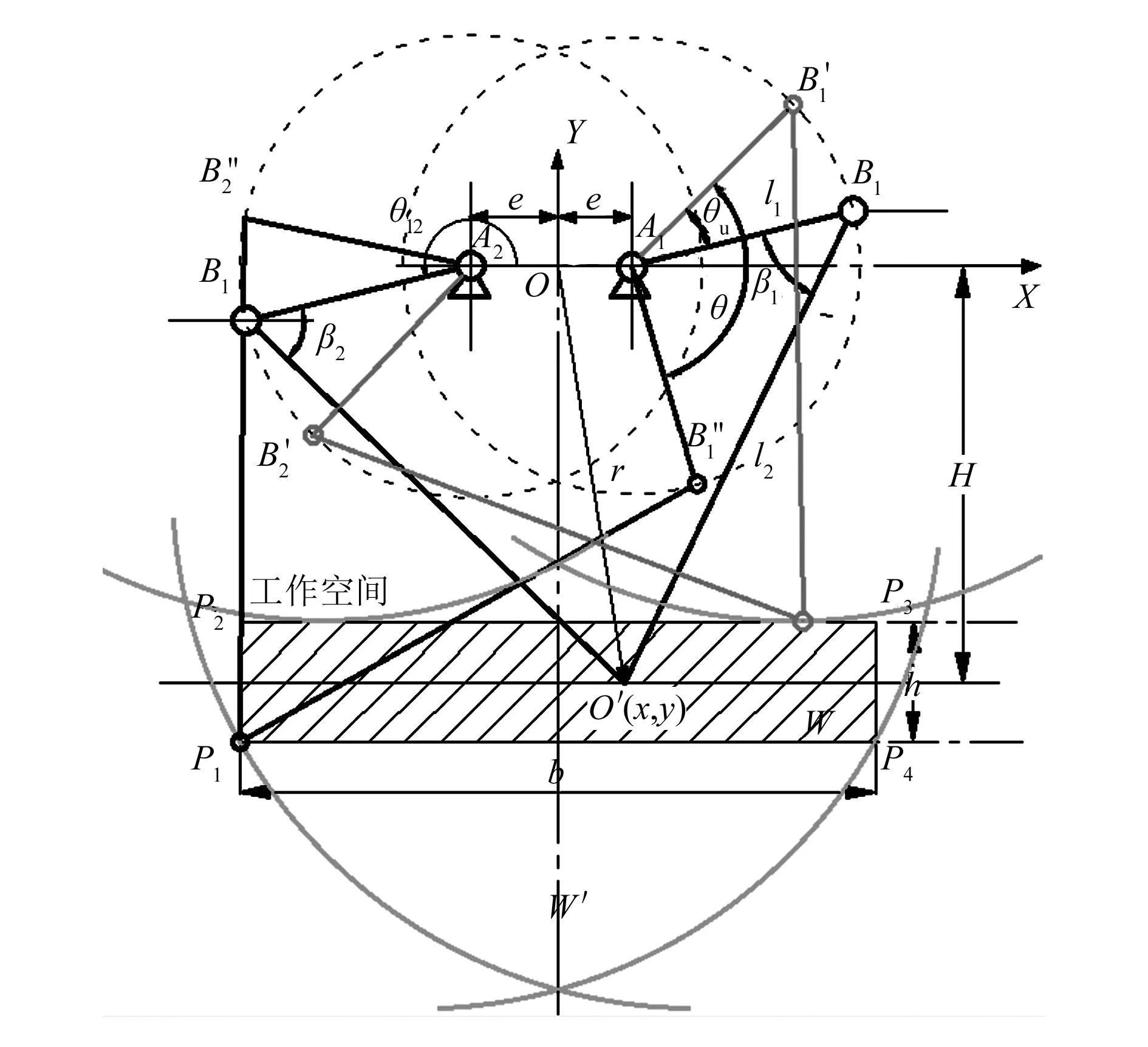
图2 机构运动简图及工作空间

2 运动学与动力学指标分析

2.1 运动学性能指标分析

本文选取速度雅可比矩阵的条件数来建立并联机器人的运动学性能指标[1]。条件数指标K(J)计算公式为：

(1)

式中：σmax为雅可比矩阵最大奇异值；σmin为雅可比矩阵最小奇异值。

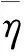
(2)

式中：K为条件数。

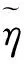
(3)

2.2 系统动力学性能指标分析

参照运动学性能指标的方法构建基于奇异值的系统动力学性能指标[5]。

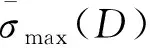
(4)

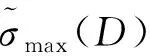
(5)

3)全域性能指标：

(6)

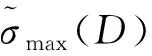
3 多目标参数优化

3.1 优化流程设计

通过对工作空间的分析可知：多目标参数的优化就是在指定工作空间内确定最优的点O距工作空间中心距离H、主动关节距原点距离e、主动臂长l1以及从动臂长l2的值，使得并联机构的全域性能指标最优。依据NSGA-Ⅱ算法以及工作空间分析，对二自由度DELTA并联机器人的结构优化设计流程如图3所示。

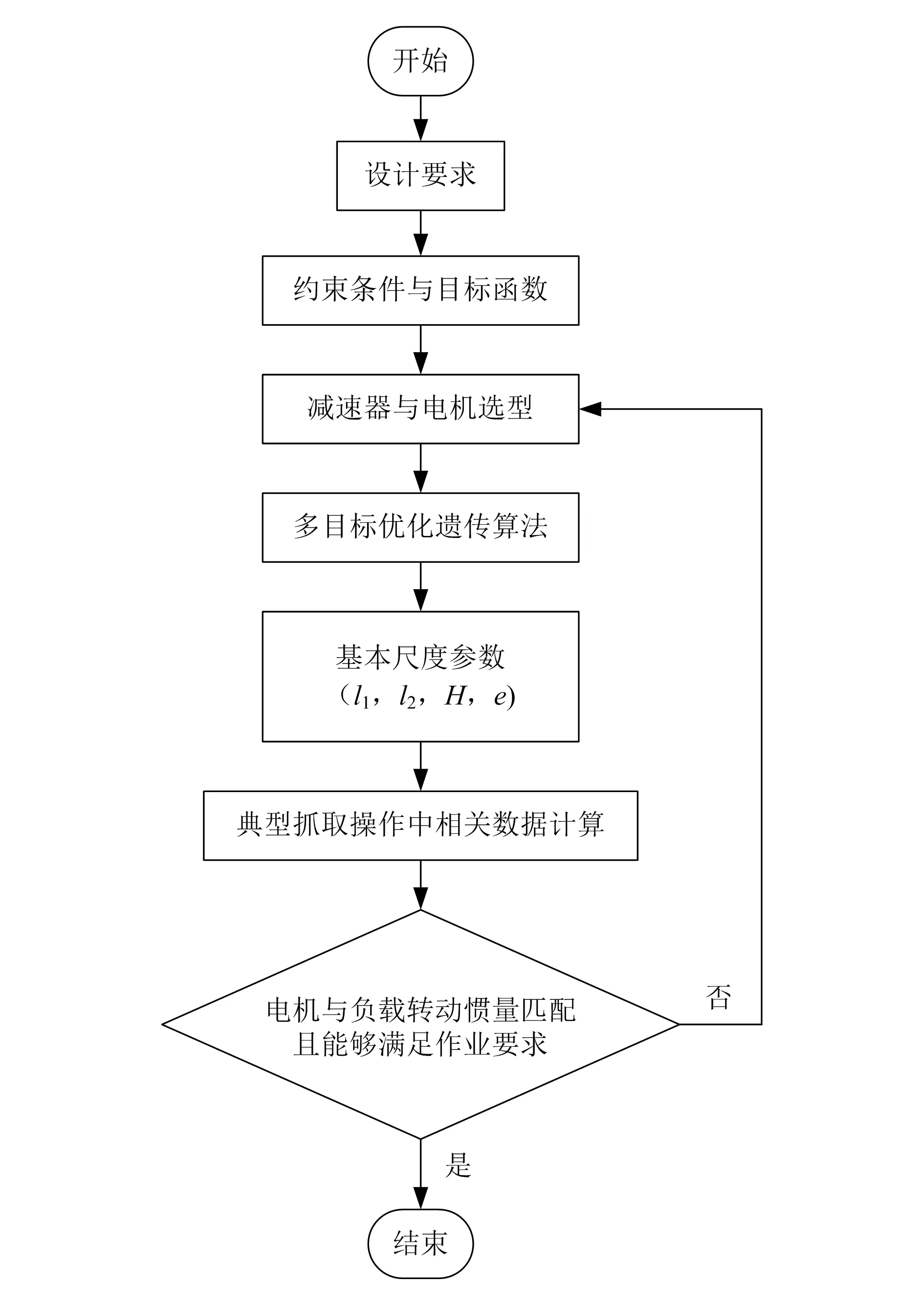
图3 优化设计流程图

3.2 多目标优化

1)约束条件。

根据并联机构的设计要求和以往设计经验，表1给出了待优化参数及其取值范围。

表1 机构零部件参数

2)目标函数。

运动学性能优化目标函数f1(x)为：

(7)

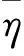
动力学性能优化目标函数f2(x)为：

(8)

3)优化结果。

为了提高系统的加减速能力，结合工作空间、负载能力、抓取次数等设计要求，优先选用小惯量电机。暂选取松下公司的MSMF012L1V2M型小惯量电机，其性能参数见表2。

表2 电机参数

在MATLAB软件中对目标函数进行求解优化，设置初始种群大小为100，进化代数最大值为500，交叉适应度函数偏差为1E-05，迭代停止次数为500，交叉概率为8，运行结束后得到第一前端个体分布图，如图4所示[6-7]。Workspace中得到函数前30个Pareto解集及目标函数值。

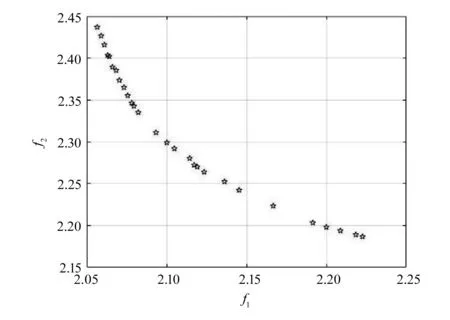
图4 Pareto前沿

采用归一化加权求和法来确定最终结构尺寸，即找出优化结果中2个目标函数各自的最小值，取其倒数为权重系数，表达式如下[8]：

minF(x)=ω1f1(x)+ω2f2(x)

(9)

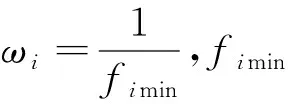
按照上述办法计算取整可得，l1=288 mm，l2=567 mm，e=60 mm，H=501 mm。

3.3 电机校核

机器人工作在0.8 m×0.15 m的矩形区域，其中心到机架距离H=0.547 m，设计动平台末端执行器最大加速度为am=3g(g=9.81 m/s2)。计算得出并联机构主动臂的角速度、角加速度、转矩和功率如图5～图8所示。

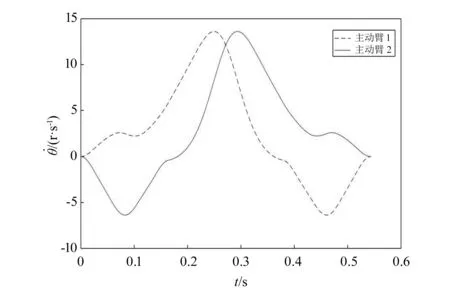
图5 典型抓取操作中主动臂角速度变化规律

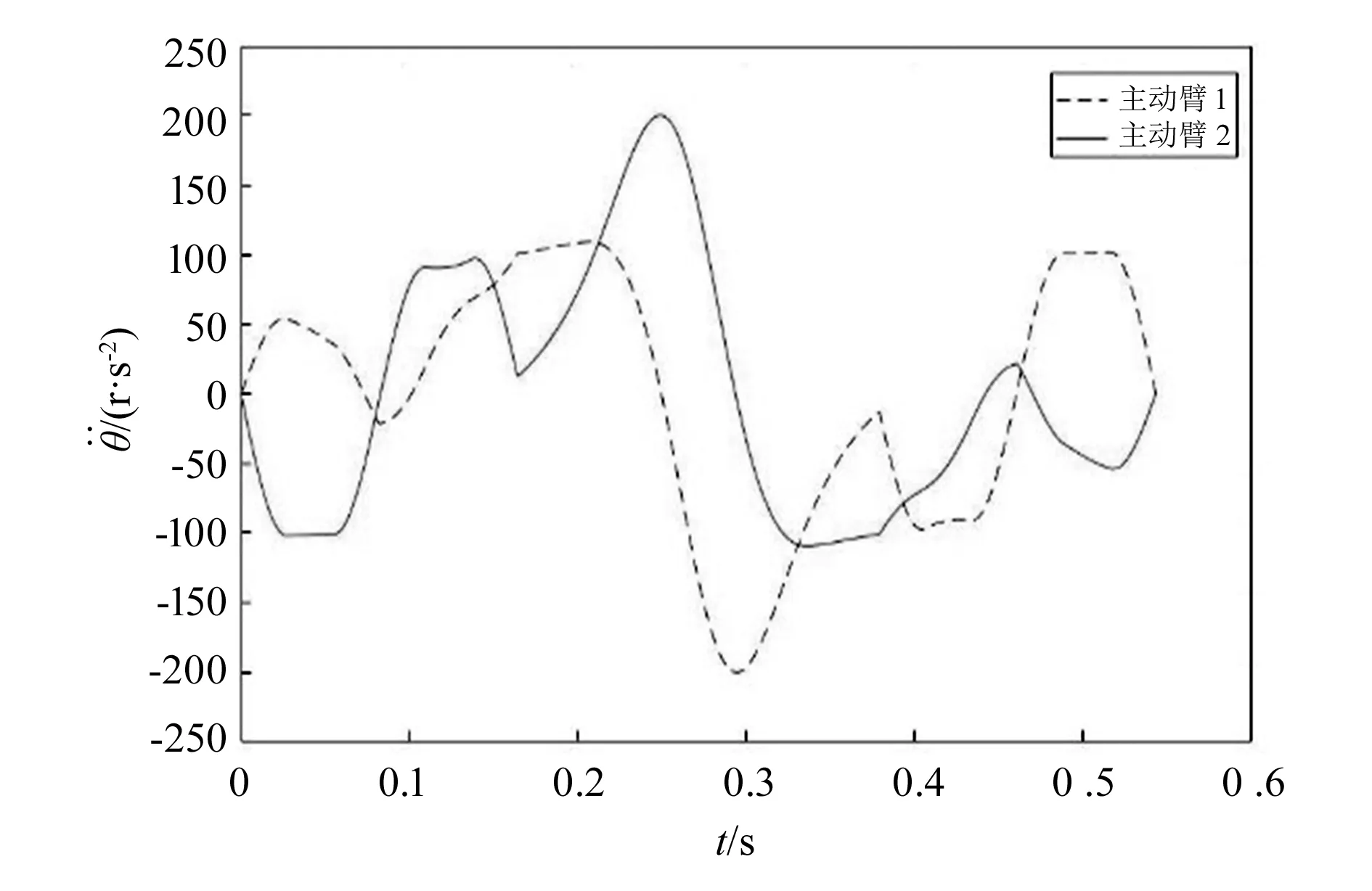
图6 典型抓取操作中主动臂角加速度变化规律

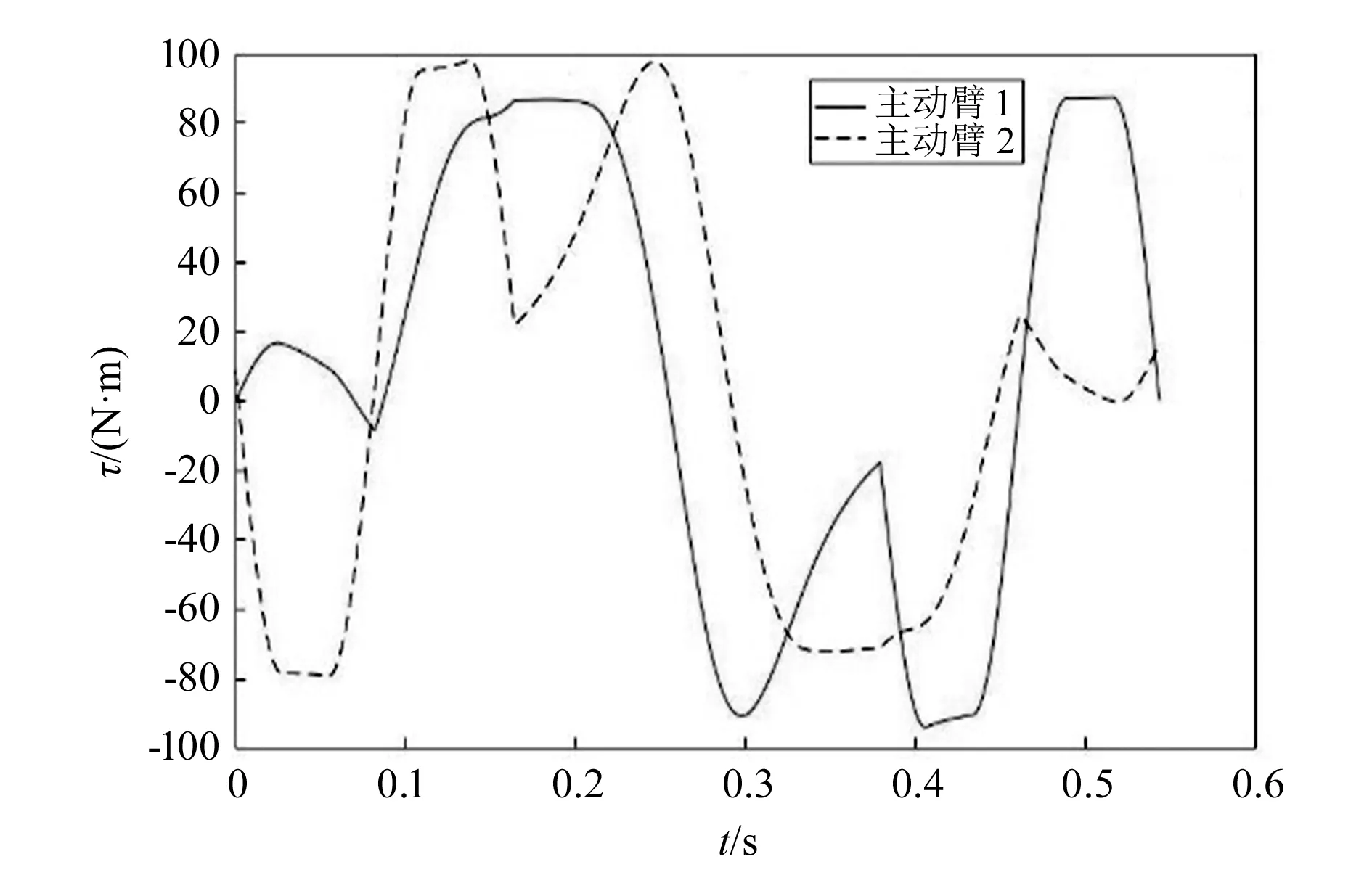
图7 典型抓取操作中主动臂转矩变化规律

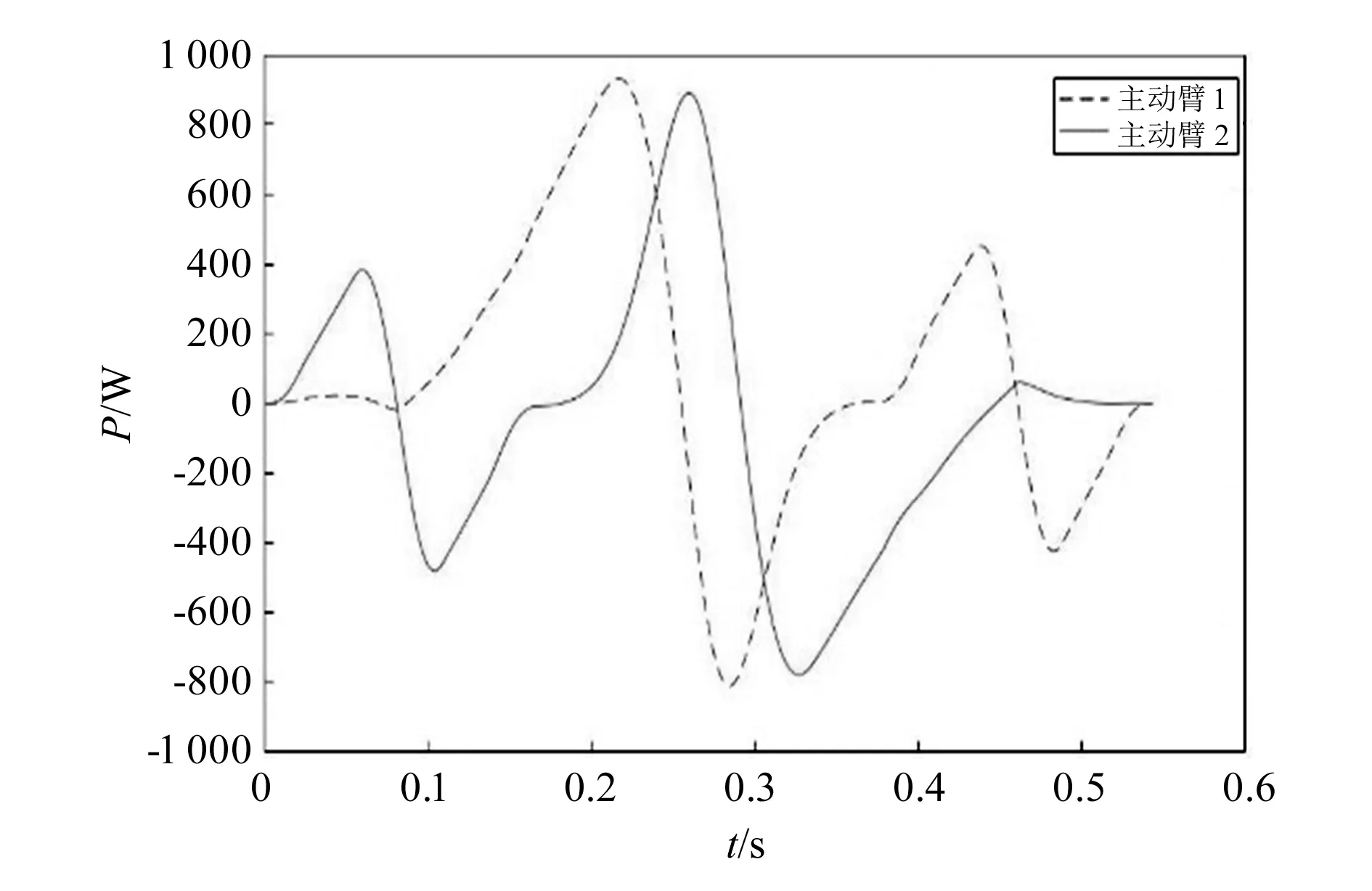
图8 典型抓取操作中主动臂功率变化规律

4 优化结果验证

图9、图10分别给出了多目标优化后的结构参数下并联机构的条件数和奇异值在工作空间中的分布情况。由图可知，条件数在整个工作空间内数值整体较小，中间部位数值最小，具有良好的运动学性能；奇异值在工作空间下半部分数值较小，具有较高的动力学性能。

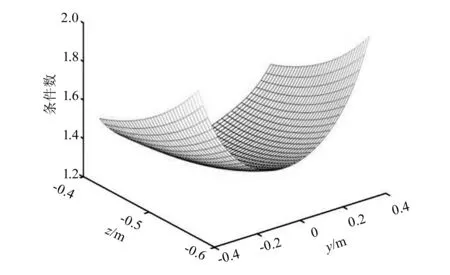
图9 多目标优化结果条件数

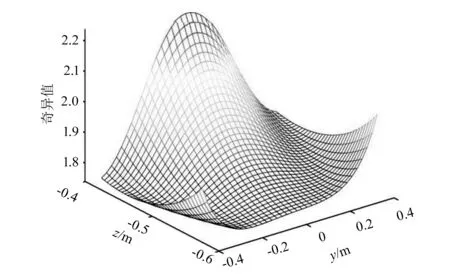
图10 多目标优化结果奇异值

将上述优化结果与文献[9]的单运动学目标优化结果及文献[10]单动力学目标优化结果进行对比，结果见表3(表中第一行为本文的多目标优化结果，第二、三行分别为文献[9]与文献[10]单目标优化方法所得到的结果)，可以看出，多目标优化结果与单运动学目标优化结果相比，运动学目标函数f1(x)的值减小了9.2%，动力学目标函数f2(x)的值减小了14.7%，F(x)值减小了12.2%；多目标优化结果与单动力学目标优化结果相比，虽然f2(x)的值增加了3.6%，但是f1(x)的值降低了8.3%，F(x)值减小了2.7%。说明针对机器人性能而言，NSGA-Ⅱ算法具有一定的优越性。

表3 优化结果对比

5 结束语

本文对二自由度DELTA并联机器人的运动学与动力学、结构进行分析，通过建立合理有效的评价指标构建目标函数，使用多目标优化算法对机器人结构参数进行优化，得到使机器人综合性能最佳的结构参数。文中研究还存在一些不足，以后将尝试同时对弹性动力学性能进行优化以进一步深入研究。