四机两区域电力系统低频振荡分析及抑制

肖伸平，李 让

（1.湖南工业大学 电气与信息工程学院，湖南 株洲 412007；2.电传动控制与智能装备湖南省重点实验室，湖南株洲 412007）

0 引言

我国电力系统行业发展迅速，超高压、重负荷、远距离的电网互联互通已是大势所趋，同时也对电力系统稳定性带来了一系列的挑战。现代电力系统是一个高维复杂的强非线性系统，IEEE 将电力系统稳定分为功角稳定、电压稳定和频率稳定三大类，功角稳定又分为小扰动稳定和暂态稳定。由四机两区域系统发电机转子间阻尼不足且缺乏足够的电磁转矩来抑制振荡，引发的转子增幅振荡属于小扰动功角失稳的范畴，振荡频率在0.2 Hz～2.5 Hz 之间，称为低频振荡［1］。R.H.Park 等学者最早提出同步发电机传统低频振荡问题［2］。实际电网运行工况复杂多样，低频振荡时有发生，是严重威胁电网安全稳定运行的重要因素。

大电网通过联络线进行的弱互联，降低了整个互联系统的动态稳定性［3］，当扰动出现时，系统极易产生低频振荡，严重时可能造成整个系统的崩溃。相关学者在低频振荡的产生机理、分析方法和抑制措施等［4］方面进行了广泛的研究，并取得了大量成果：文献［5］利用MATLAB 搭建了含双馈感应发电机的风电并网系统，将电力系统稳定器应用到系统以抑制其低频振荡；文献［6］研究了柔性直流输电系统产生的低频振荡，并采取了多种控制手段来抑制低频振荡；文献［7］在DIgSILENT 平台上通过双馈风电机组仿真研究分析其低频振荡阻尼控制策略的性能；文献［8］在系统中加入电池储能装置来抑制低频振荡。综合以上学者研究，对四机两区域系统低频振荡建模的研究很有必要。

本文针对典型的四机两区域系统，通过建模研究该系统低频振荡的产生及抑制，利用时域仿真对一定运行方式下的系统施加不同小扰动，对联络线三相接地短路和励磁参考电压突变故障进行仿真，观察小扰动后系统各发电机输出功率、转子转速及联络线传输功率等随时间摆动的情况。并在发电机的励磁系统Vstab 端接入多频带电力系统稳定器（MB-PSS）和通用型电力系统稳定器（G-PSS）的输出信号来抑制系统产生的低频振荡。四机两区域算例广泛用于电力系统稳定性的相关研究［9］，具有普遍性和实用性，对低频振荡的研究具有一定的参考意义。

1 四机两区域电力系统建模

1.1 四机两区域系统结构

四机两区域系统也称Kundur 系统，1994 年由电力系统大师Prabha S.Kundur 在经典著作《电力系统稳定与控制》一书中提出，其系统结构如图1 所示，该系统包括两个用一条220 km 联络线连接的虚线框内的相似区域，区域1 与区域2 的系统容量较大，在电力系统发生扰动的情况下很容易失稳。

图1 四机两区域系统结构图Fig.1 System structure diagram of the two areas with four generators

两个区域中均有两台耦合的机组，分别是发电机G1、G2 与G3、G4，系统相关参数参照文献［1］设置。系统负荷模型为恒阻抗负荷L7、L8，分别连接于7 号母线与9 号母线处；C7、C8 为无功补偿电容器，为系统提供无功功率。

1.2 四机两区域系统仿真模型

利用MATLAB/Simulink软件对Kundur系统进行仿真，研究存在弱联系的两个区域易受到小扰动干扰，造成机组间的振荡不稳定，仿真包含同步发电机、三相变压器、励磁调速器、分布参数线以及三相故障块等模型。

图2 为Kundur 系统的仿真模型总图。封装好的区域1 和区域2 通过220 km 的线路进行弱联系，在线路上设置三相故障块（Three-Phase Fault）。

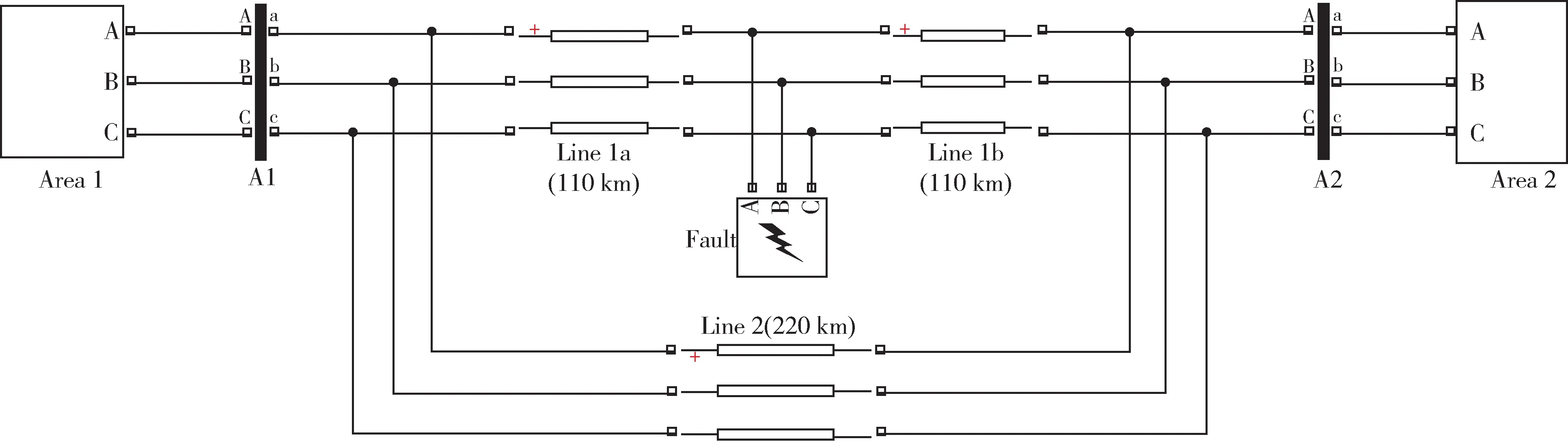
图2 四机两区域系统仿真模型总图Fig.2 General layout of simulation model for the two areas with four generators

图3 为区域1 的仿真模型示意图，包括一组耦合的发电机G1、G2，以及两个变压器T1、T2，7 号母线处设置了负荷模型和并联电容器为系统提供无功功率，两组耦合的系统通过6 号母线经10 km 的输电线路接入总系统。区域2 与区域1 区别在于参数设置不同。

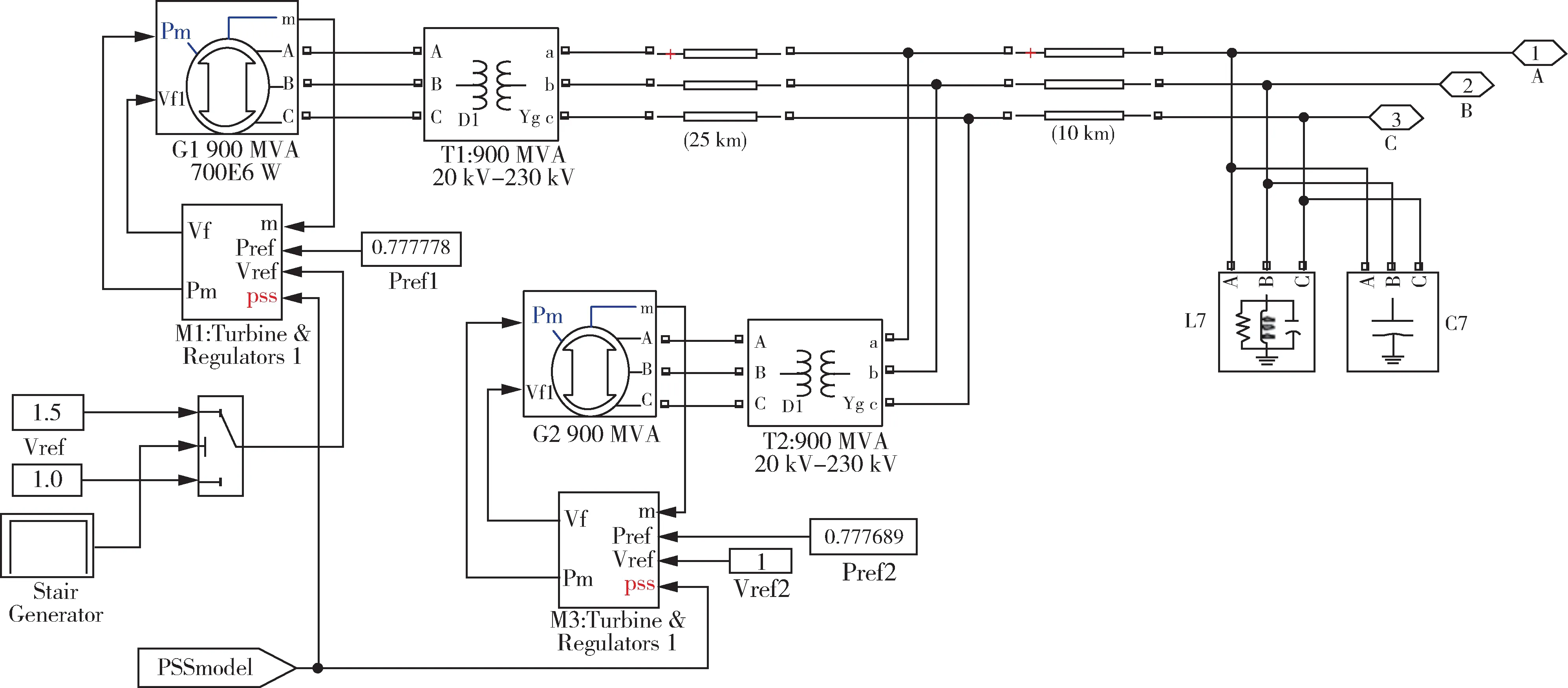
图3 区域1 仿真模型Fig.3 Simulation model of area 1

图4为G1的励磁调速系统仿真模型，4台同步发电机均配备了励磁调速系统，包括励磁调速器（Excitation）和汽轮机调速器（STG），在励磁系统的Vstab输入端引入两种类型的PSS，用来抑制该系统产生的低频振荡。

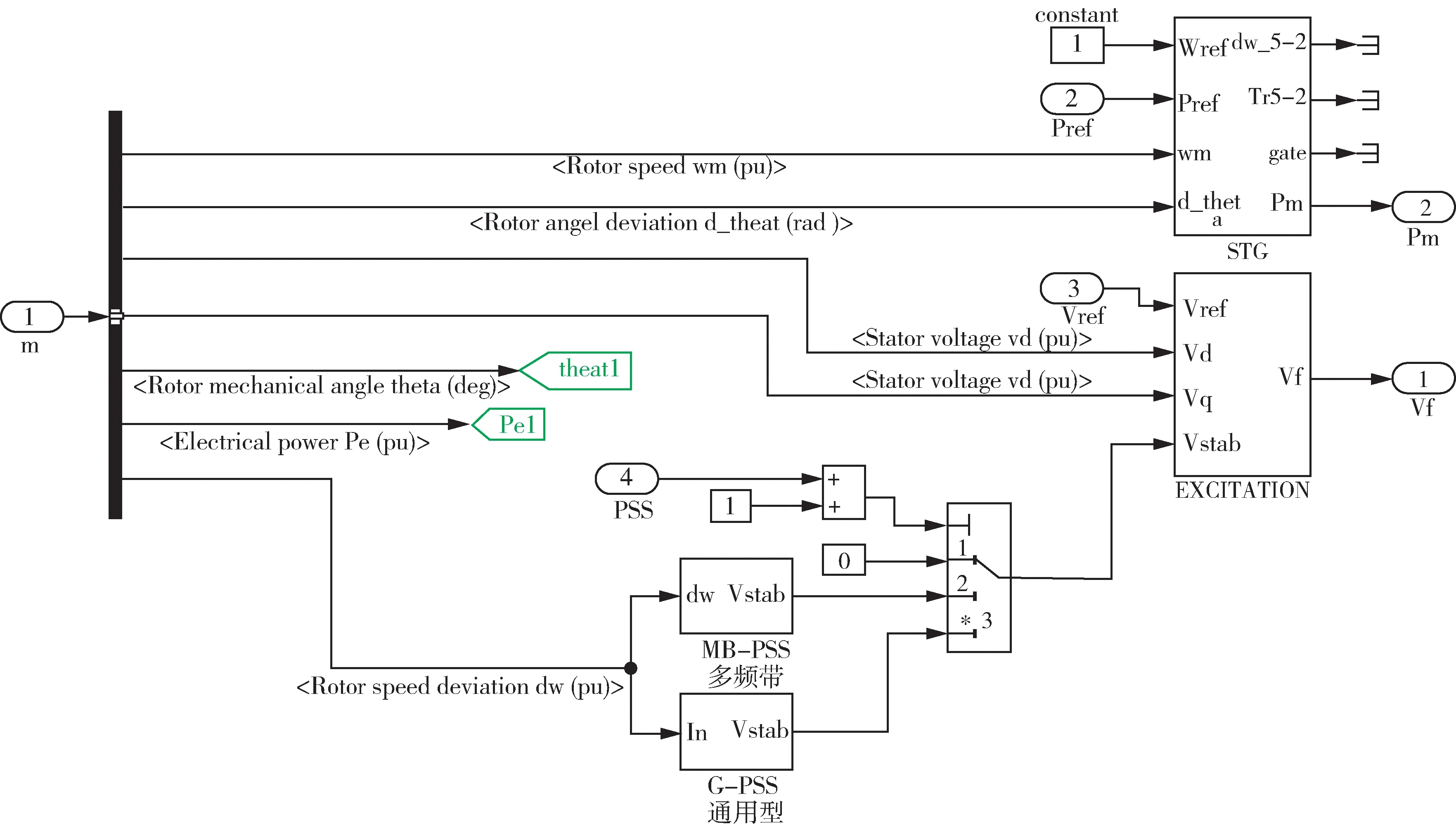
图4 发电机G1 励磁调节系统仿真模型Fig.4 Simulation model of excitation regulation system of generator G1

1.3 模型参数设置

同步发电机G1、G2、G3、G4 参数基本相同，额定容量为900 MV·A，额定电压为20 kV。其他参数标幺值：d轴对应的同步电抗Xd=1.8 p.u.，暂态电抗X′d=0.3 p.u.，次暂态电抗X′′d=0.25 p.u.；q轴对应的同步电抗Xq=1.7 p.u.，暂态电抗X′q=0.55 p.u.，次暂态电抗X′′q=0.25 p.u.；Xl=0.2 p.u.。发电机励磁绕组对应的暂态时间常数T′d0=8 和次暂态时间常数T′′d0=0.03；阻尼绕组对应的暂态时间常数T′q0=0.4、次暂态时间常数T′′q0=0.05，定子电阻Rs=0.002 5，极对数p=4；另外，G1 与G2 的惯性系数为H=6.5，G3 与G4 的惯性系数为H=6.175。

变压器模型参数：T1、T2、T3、T4 基准容量900 MV·A，变比均为20/230 kV。

无功补偿电容C7 的标称相间电压为230 kV，感应无功功率QL=0，电容无功功率QC=200 MVar；C8 标称相间电压为230 kV，QL=0，QC=350 MVar。

负荷L7 参数的有功功率P=967 MW，QL=100 MVar，QC=187 MVar；重负荷L8 参数的P=1 767 MW，QL、QC与L7 的设置相同。

励磁调节系统参数：放大倍数Ka=200，时间常数Ta=0.001。

2 仿真实验

2.1 三相接地短路故障仿真

在四机两区域系统联络线上连接三相故障块，设在1 s 时发生A、B、C 三相接地短路故障，持续时间约为0.2 s，系统仿真如图5 所示。图5（a）中三个波形分别是G1、G2、G3 与G4 的机械角乘以极对数得到功角度的差值。文中选取一台发电机G1 观测其参数变化，图5（b）是G1 的转子转速，图5（c）是G1 的输出功率，图5（d）是区域1 向区域2 的联络线传输功率。

由图5（a）可知，同一区域的一组发电机联系较强，功角变化趋势相似。当系统受到扰动时，发电机的转子转速和输出功率均发生振荡，且随着时间增加，振幅越大，系统处于不稳定状态。

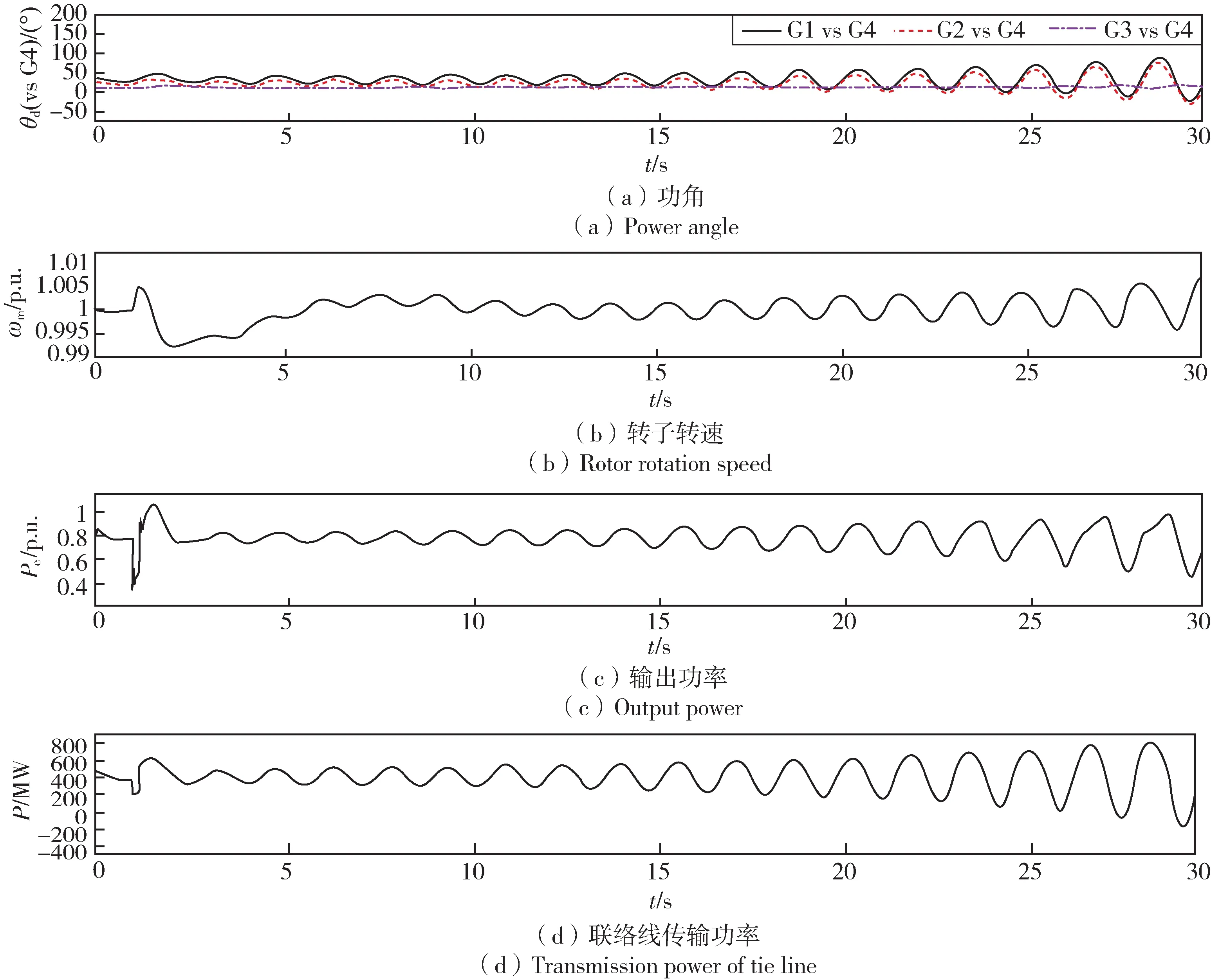
图5 三相接地短路仿真Fig.5 Simulation of three phase grounding short circuit

2.2 励磁参考电压突变仿真

系统中发电机均配备励磁调速系统，在图3 中区域1 的发电机G1 励磁参考电压Uref输入端连接阶梯生成器Stair Generator 使得励磁参考电压在1 s 时发生从1 到1.5 的突变，仿真如图6 所示。由图6 可得系统中发电机转子转速、输出功率和区域传输功率均发生了大幅度的振荡，可见励磁参考电压突变引起的振荡均强于三相接地短路造成的振荡。

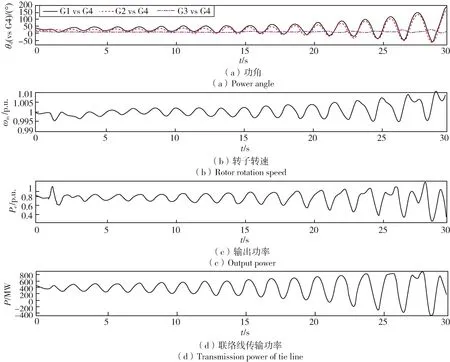
图6 励磁参考电压突变仿真Fig.6 Simulation of sudden change of excitation reference

3 低频振荡抑制策略

目前，提高系统功角稳定性的措施主要包括一次系统和二次系统两方面的对策［10］，但一次系统抑制措施投资大且互联电网情况复杂，不适用于低频振荡的抑制，一般采用二次系统策略。具体可分为：（1）励磁控制，设计各种励磁控制器，在励磁回路施加附加阻尼控制；（2）柔性交流输电系统设备，包括静止无功补偿器（SVC）装置［11-12］和可控串联电容补偿等附加阻尼；（3）PSS 是通过附加系统提供合适的正阻尼抵消系统负阻尼来抑制低频振荡等。

在各种阻尼控制方式中，利用励磁控制最为经济有效［13］。文献［14-15］研究了发电机励磁系统引入调差单元对低频振荡的影响。本文在发电机励磁系统的Vstab 输入端引入PSS 抑制低频振荡，文中采用MB-PSS 和G-PSS 两种PSS 抑制低频振荡，MB-PSS 参数为低频段频率FL=0.2，增益KL=30；中频段FI=1.25，KI=40；高频段FH=12，KH=160。G-PSS 参数：时间常数T=0.001 5，增益K=30，冲洗时间常数为10。

如图7 和图8 所示分别是MB-PSS 和G-PSS 抑制三相接地短路的发电机转子转速、输出功率和联络线传输功率的时域仿真，通过对比可看出，对于三相接地故障引起的低频振荡，G-PSS 抑制效果比MB-PSS更好，尤其是转子转速的变化较为明显。

图7 MB-PSS 抑制三相接地短路Fig.7 Suppression of three phase grounding short circuit by MB-PSS

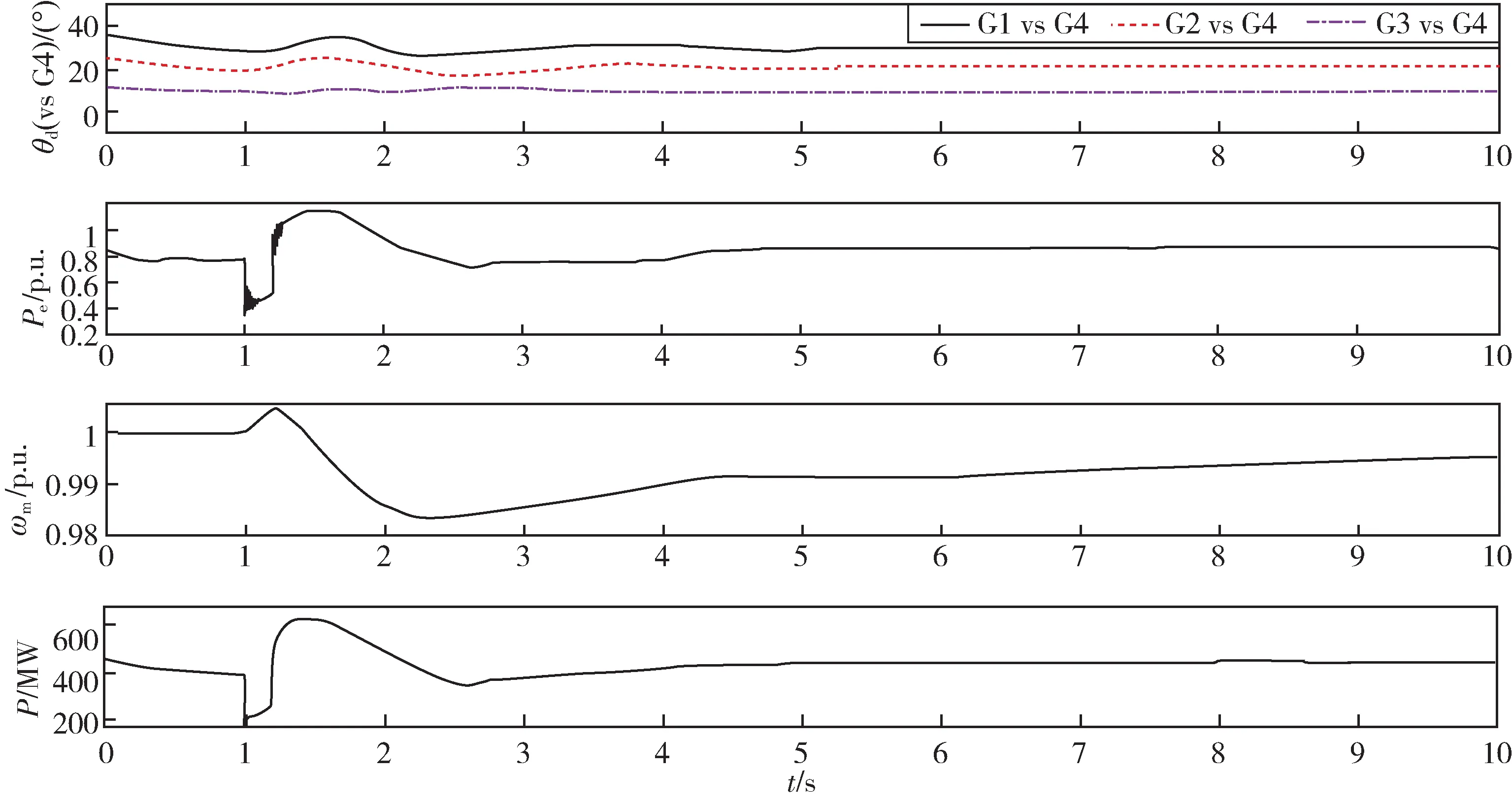
图8 G-PSS 抑制三相接地短路Fig.8 Suppression of three phase grounding short circuit by G-PSS

如图9 所示是四台发电机励磁系统参考电压发生突变后发电机参数仿真图，可看出发电机参数发生振荡，联络线传输功率处于不稳定状态。在励磁系统加入MB-PSS 和G-PSS 来抑制系统低频振荡，仿真结果如图10 和图11 所示。

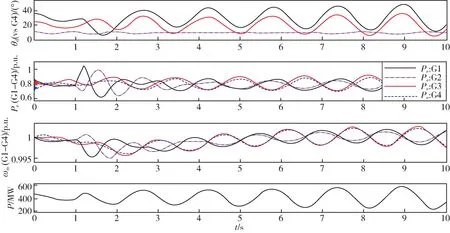
图9 励磁参考电压突变仿真Fig.9 Simulation of sudden change of excitation reference voltage

图10是MB-PSS 抑制励磁参考电压突变的发电机转子转速、输出功率和联络线传输功率的时域响应图，图11是G-PSS 抑制仿真。由图可知，两种类型的PSS均能较好地抑制由于励磁参考电压突变所引起的低频振荡。

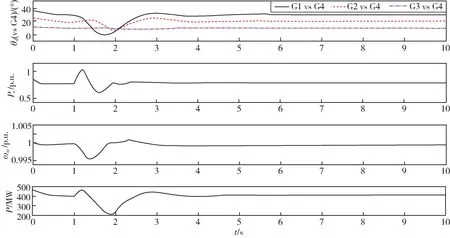
图10 MB-PSS 抑制励磁参考电压突变Fig.10 MB-PSS suppresses sudden change of excitation

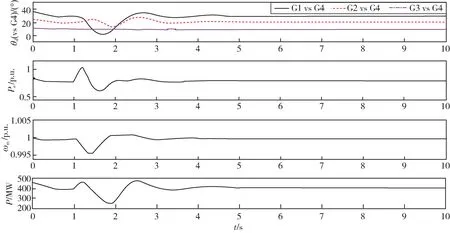
图11 G-PSS 抑制励磁参考电压突变Fig.11 G-PSS suppresses sudden change of excitation reference voltage reference voltage

4 结语

本文利用MATLAB/Simulink 搭建了典型的四机两区域系统，通过设置两种常见故障，即三相接地短路和励磁参考电压突变，测试该系统在对应扰动情况下发电机转子转速、输出功率及联络线功率的时域响应。分别对故障设置两种PSS 抑制措施，即MB-PSS 和G-PSS，通过仿真比较两种PSS 抑制系统低频振荡效果。结果表明，联系较弱的系统受到干扰极易产生低频振荡，严重时系统甚至会解列，三相接地短路故障使用G-PSS 效果更佳，而两种PSS 对励磁参考电压突变故障引起的低频振荡均有较好的抑制效果。