岩石巷道爆破效果预测及应用效果实践研究

马鑫民，王 毅，翟中华，冯文宇，朱培枭，陈 攀，张召冉，王雁冰

(1.中国矿业大学(北京)力学与建筑工程学院，北京 100083；2.北方工业大学 土木工程学院，北京 100144)

爆破在矿山开采的总成本中所占比例虽然不大，但爆破效果的优劣往往会给后续工作如铲装、运输、破碎等带来较大的影响，因此其是矿山安全高效开采的关键技术之一[1]，而爆破效果的优劣是评价掘进质量好坏的重要指标。如何通过科学的方法开展爆破效果预测，并据此调整优化爆破参数，进而提升爆破效果具有重要的理论和工程实际意义。通过爆破智能预测可以比较准确地预测出当前生产条件下爆破效果。此技术能给予在现场施工的技术人员更多合理的经验性知识，辅助他们因地制宜地进行现场的方案调整。

爆破效果预测在国内外都属于新兴的研究方向，预测的办法也是百花齐放。支持向量机(Support Vector Machine，简称 SVM)因其对小样本、高维度的数据更敏感，在爆破效果预测中被广泛使用或联合其他算法使用[2-9]。针对爆破效果预测存在的不足，本文提出基于改进的SVM算法进行爆破效果预测研究，既充分发挥SVM的优点，又具有创新性。提出目前研究较少的预测爆破的炸药单耗，通过网格搜索交叉验证算法与SVM算法结合提升预测的准确性；利用免费开源、用途广泛、语言简单的Python平台进行建模预测及输出数据；利用随机森林重要性排序筛选合理的预测因素，综合提升预测准确率及可操作性，更贴合工程人员的实际需求。

1 算法原理

1.1 SVM算法

SVM是一种有监督的机器学习算法[10-15]，其中心思想就是利用某些支持向量所构成的“超平面”，将不同类别的样本点进行分类[16，17]。

假设线性分割面表示为w′x+b=0，则点到分割面的距离可以表示为：

(1)

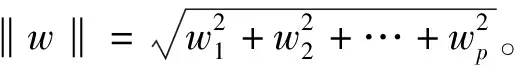
SVM可以解决连续型数据的预测问题，称为SVM回归，简称SVR，需要计算出上式中的w与b。对于线性回归，加入松弛因子ξ(*)，确保不等式|yi-f(xi)|-ξ(*)≤ε成立，即：

(2)

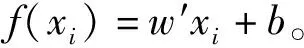
整理得关于目标函数的极大值问题，即：

(3)

(4)

在实际中遇到的样本基本都是高维且非线性可分的，需借助于核函数技术，实现样本在核空间下完成线性可分。需要使用核函数K(xi，xj)技术替换更高维的空间内积，函数f(xi)可以表示为：

(5)

选择SVM适配的三种核函数，具体见表1。

表1 使用的核函数种类

1.2 Grid Search CV算法

Grid Search CV(Cross Validation)，由网格搜索和交叉验证两部分组成[18，19]。

Grid Search(网格搜索)的目的是寻找最优参数，即在指定的参数范围内，按步长依次调整参数，利用调整的参数训练学习器，遍历所有可能参数的组合，从中找到在验证集上精度最高的参数。

这种方法虽然简单易行，但是其最终的表现好坏与初始数据的划分结果有很大的关系，为了降低偶然性，可采用交叉验证的方式来予以辅助。

Cross Validation(交叉验证)的基本思想是把将原始数据进行分组，一部分作为训练集，另一部分作为测试集，先用训练集对分类器进行训练，再用测试集来测试训练得到的模型，以此作为评价分类器的性能指标。

采取K折交叉验证，若K=10，就是十折交叉验证，其运算步骤如下：

1)将所有数据集分成10份。

2)不重复地每次取其中1份做测试集，用其他9份做训练集训练模型，之后计算该模型在测试集上的MSEi。

3)将10次的MSEi取平均得到MSE。即：

(6)

一般来说折数不宜过多，K=5或K=10较为常用，通过比对每一组数值，可以求得选定范围内使预测准确率最高的参数。

1.3 Grid Search CV与SVM融合方法

虽然SVM模型对爆破预测有很大优势，但是SVM还有核函数的参数不易调整的缺点。为了克服这一缺点，引用Grid Search CV算法来进行合理的参数寻优，提升SVM算法的准确率。

本文使用非线性可分SVM模型，选择使用径向基核函数“Rbf”、多项式核函数“Poly” 和线性核函数“Linear”三种核函数作为对比验证，用网格搜索法来进行它们的参数寻优。

在这三种核函数中，有两个重要的参数，即C和gamma。C表示模型对误差的惩罚系数，gamma反映了数据映射到高维特征空间后的分布。这两个参数的大小将会一定程度上改变预测的结果。

网格搜索法需要在SVM建模之前进行，使用K折交叉验证，K-CV交叉验证重复k次，其显著的优点是所有的样本都被作为了训练集和测试集，每个样本都被验证一次。在SVM算法下，将全体数据拆分为训练集和测试集，按照预先设定好的K折，经过计算，将其中平均得分最高的超参数组合作为最佳选择，将这些参数传递给SVM的核函数，以便进行下一步的SVM预测。

在实际运用中，可利用Python中的sklearn子模块下的“sklearn.model_selection import GridSearchCV”模块实现参数的寻优。

1.4 随机森林算法原理

随机森林(Random Forest)算法作为对照组，其核心思想是采用多颗决策树的投票机制来完成预测，其基本原理是运用Bootstrap抽样法从数据集中随机抽取多个样本，为每一个样本进行决策树建模，在给每个结点划分属性时，从该节点的属性集合中随机抽取一个子集，选取该子集中的最优属性用于划分；最后组合多棵决策树的预测，得出预测结果[23]。其中，Bootstrap重抽样方法中每个样本未被抽取的概率为：

(7)

当N→+∞时，每个样本未被抽取的概率为：

(8)

其中，N为原始训练集中样本的个数。

2 关键指标选取与预测流程

2.1 影响爆破效果关键因素初步确定

本文使用的爆破数据库由线上收集和现场收集两部分组成，具体收集流程如图1所示。岩石巷道爆破方案决策涉及的参数多且复杂，为提高预测准确性，在众多因素中初步挑选出5大类、共18个比较重要的因素。

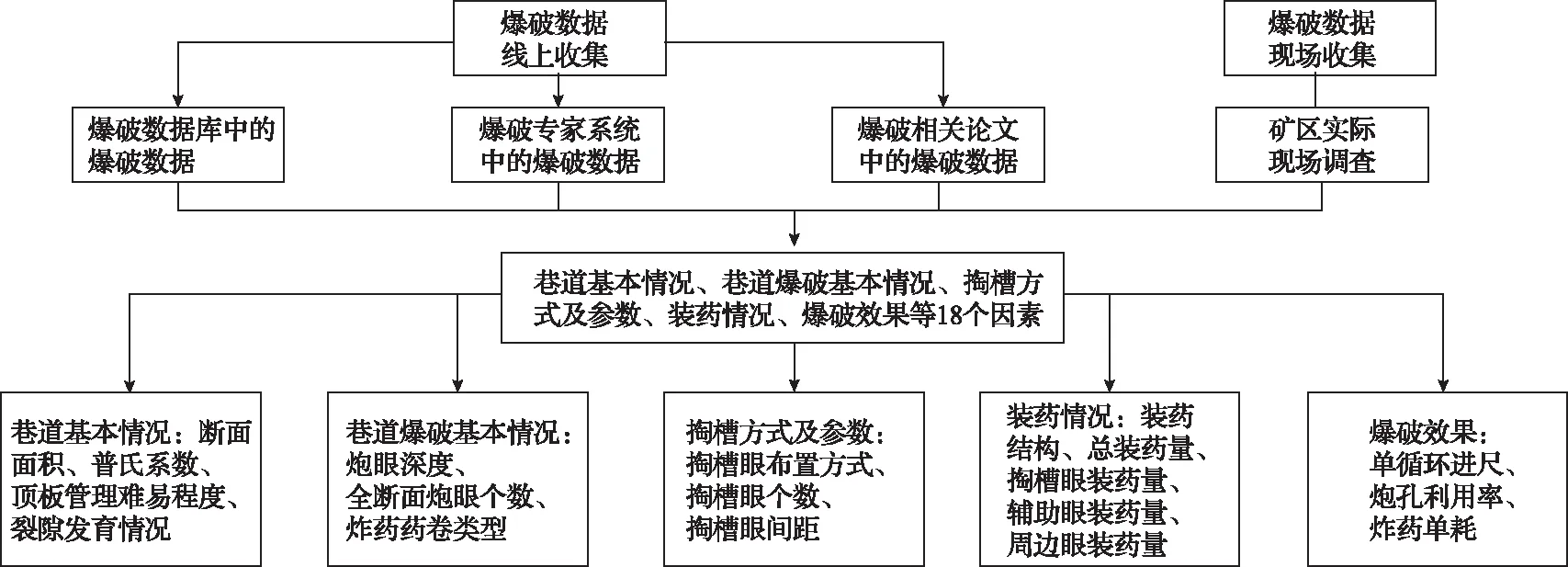
图1 爆破数据收集流程

2.2 数据的预处理

共收集整理76组爆破数据，部分数据有缺失或者不合理的地方，运用爆破经验进行合理的补充、或替换，有利于进行预测，处理后见表2。

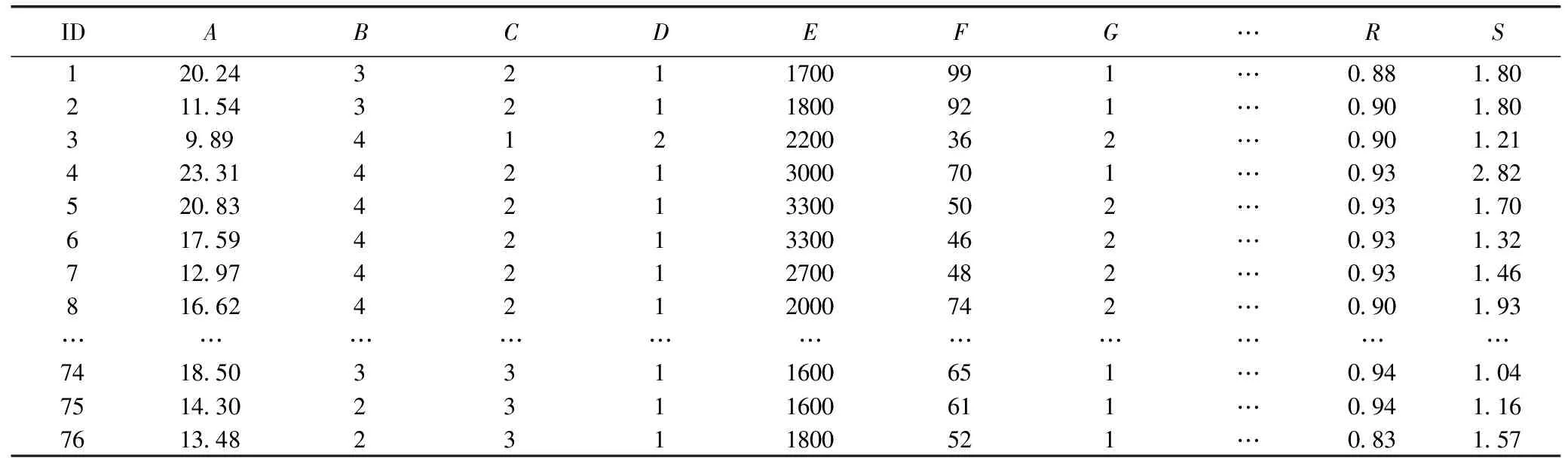
表2 预处理后的爆破数据库的数据

2.3 数据的归一化

表2的数据并不利于预测，这些数据的大小和量级不同，预测时易造成数据间的欧式距离不准，导致预测准确率不足，为了让不同维度之间的特征在数值上有一定的比较性，需要进行数据的归一化来提升预测的准确率和运算速度。

为了消除数据特征之间的量纲影响，需要对各个特征进行归一化处理，使得不同指标之间具有可比性，本文选用线性函数归一化。它对原始数据进行线性变换，使结果映射到[0，1]的范围，实现对原始数据的等比缩放[24]。其公式如下：

(9)

式中，x*为某一样本归一化后的值；x为某一样本的值；max为样本数据的最大值；min为样本数据的最小值。

将表2的数据进行归一化，结果见表3，为建模预测打下良好的基础。

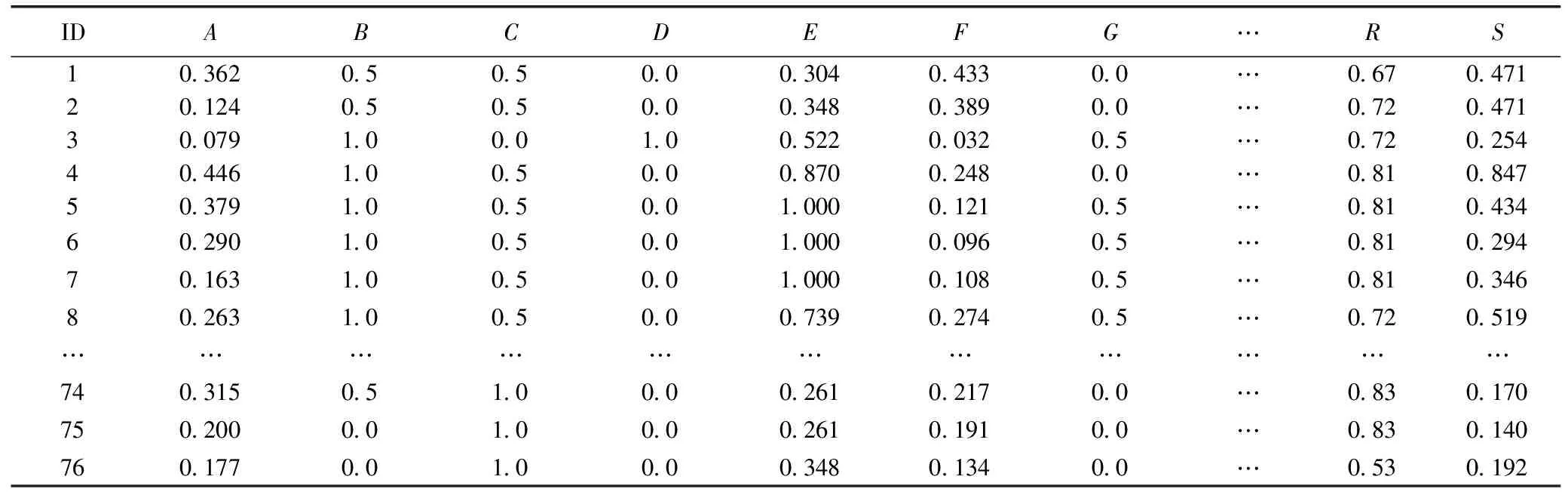
表3 经整理及归一化后的爆破数据库的数据

2.4 预测流程

1)引入Python中的sklearn机器学习库的相关程序包，作为预测算法的前置准备，sklearn机器学习库在智能预测中有很强的适用性。

2)根据爆破现场情况和文献中的相关理论经验合理地补充或修改数据库中的数据，运用公式(9)将数据归一化。

3)将预处理后的爆破数据运用Python随机分为训练集和预测集，在数据库自身预测中训练集约占总体数据的70%，测试集约占总体数据的30%。

4)对SVM适配的三种核函数的参数使用网格搜索法进行寻优，通过交叉验证可以确定参数的取值。

5)将上一步得到的参数运用sklearn机器学习库中的SVR函数预测炸药单耗，可得出预测结果。

6)将数据可视化并分析预测结果以得结论。

预测流程如图2所示。

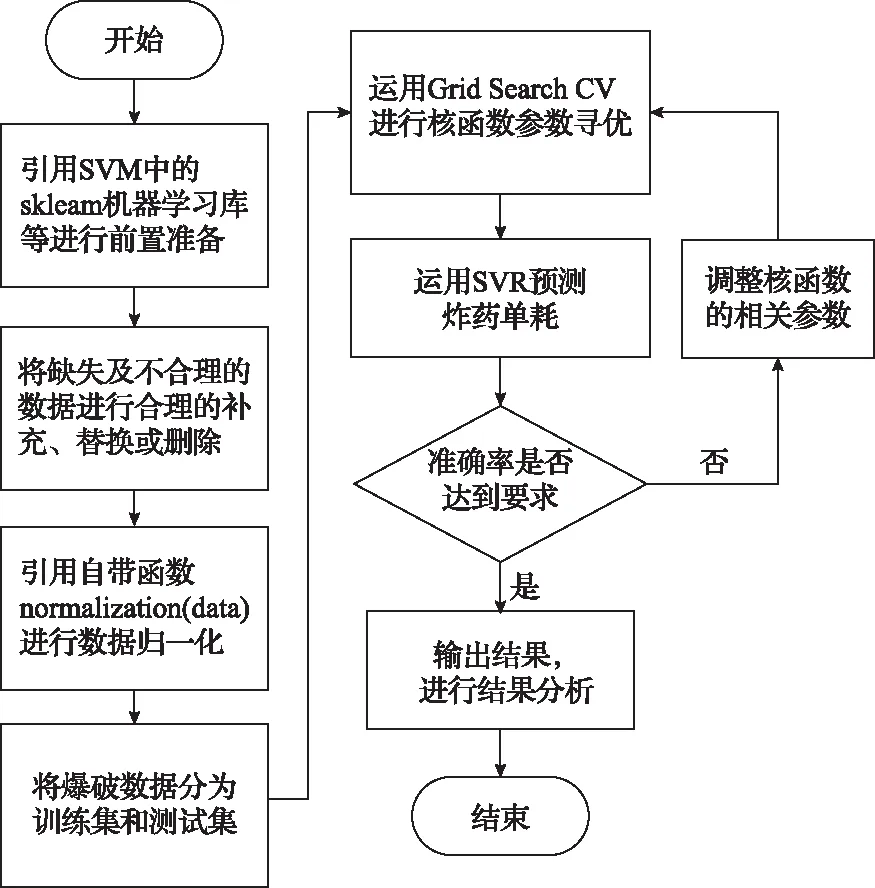
图2 Grid Search CV-SVM预测流程

2.5 选择合理的因素进行预测

通过初步预测，发现预测的炸药单耗的准确性不高，其相关系数为0.55～0.65之间，运用随机森林算法中的重要性排序功能，对炸药单耗预测进行因素重要性排序，排序结果如图3所示。考虑可能是因为因素太多导致效果不佳，依次将重要性低的因素剔除并重新建模预测，当剩余6种重要因素时(总装药量、掏槽眼装药量、周边眼装药量、炮眼深度、辅助眼装药量、断面面积)预测的最好，将这种预测方法应用于实际案例中，结果表现良好。

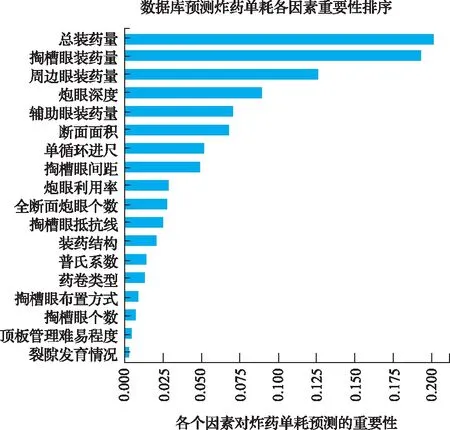
图3 爆破数据库炸药单耗预测重要性排序

3 预测模型的结果与分析

3.1 爆破数据库案例预测结果与分析

运用2.5节的结论进行建模预测，可以得到多项式核函数、径向基核函数以及线性核函数三类核函数匹配的SVM在爆破数据库下对数据库自身的炸药单耗回归预测的数据，同时展示同条件下随机森林的预测数据作为对比，这四种预测参数和预测结果(平均绝对误差“MAE”、均方误差“MSE”、解释回归模型的方差得分“Explained_variance_score”、相关系数“R2_score”)见表4。

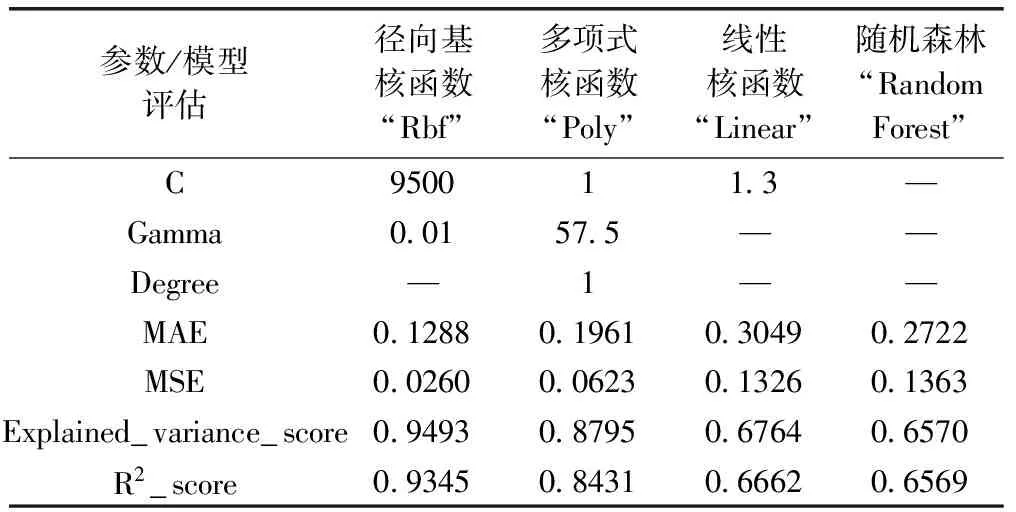
表4 爆破数据库炸药单耗回归预测结果对比

随机分配训练集53组，预测集23组，四种函数预测的效果对比和误差对比如图4、5所示。

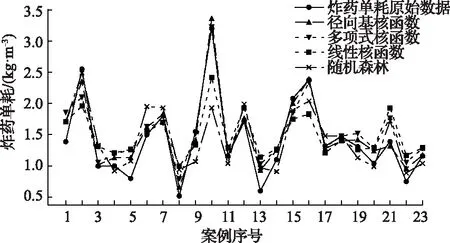
图4 四种函数对爆破数据库中炸药单耗的回归预测结果与原始数据对比图

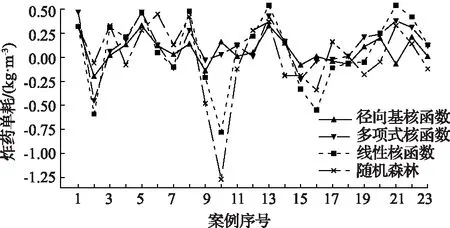
图5 四种函数对爆破数据库中炸药单耗的回归预测误差对比

通过以上的参数和图像可以发现SVR-Rbf组相较于其他三组都有绝对的优势，其相关系数为0.934，平均绝对误差也只有0.129，表现非常出色同时发现随机森林在本组的表现与SVR-Linear组相似，但不如SVR-Poly组，随机森林相较支持向量机预测精度相对较差。

对所得数据进行进一步分析，绘制四种函数的误差直方图，发现SVR-Rbf组的误差范围最小，核密度值最大，从各方面综合来看SVR-Rbf组预测效果最好，数据如图6所示。

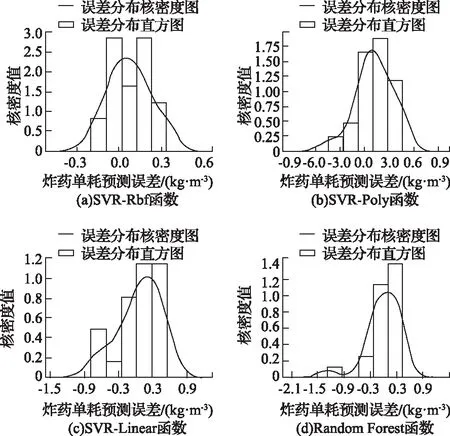
图6 四种函数对爆破数据库中炸药单耗的预测误差直方图和核密度分布

在以爆破数据库自己为训练集和预测集的预测中，SVM技术，尤其是SVR-Rbf组展现出了比较好的预测能力。接下来将把现场实际的数据带入爆破数据库中去预测，验证爆破数据库的能否支持现场的实际需要。

3.2 顾北煤矿案例预测结果与分析

顾北煤矿位于安徽省淮南市凤台县，其地层的岩性主要为粉砂岩、粉细砂岩、中细砂岩、细砂岩、煤等；(煤)岩层裂隙、滑面发育；局部发育小褶曲；岩石普氏系数f在4～5之间。

为验证模型的预测效果，选取顾北煤矿中实测的23组数据作为预测集，而原爆破数据库中的76组数据作为训练集，进行预测，部分数据见表5。

表5中的数据均为现场实测收集，实际案例数据同样经过数据处理过程，再运用四种函数进行预测，最终得出预测的结果。通过比较相关系数等参数，可以得出径向基核函数表现最好，多项式核函数稍逊，径向基核函数更次之，对照组随机森林在实际案例中表现不如前面三种函数。具体的参数和预测结果见表6。

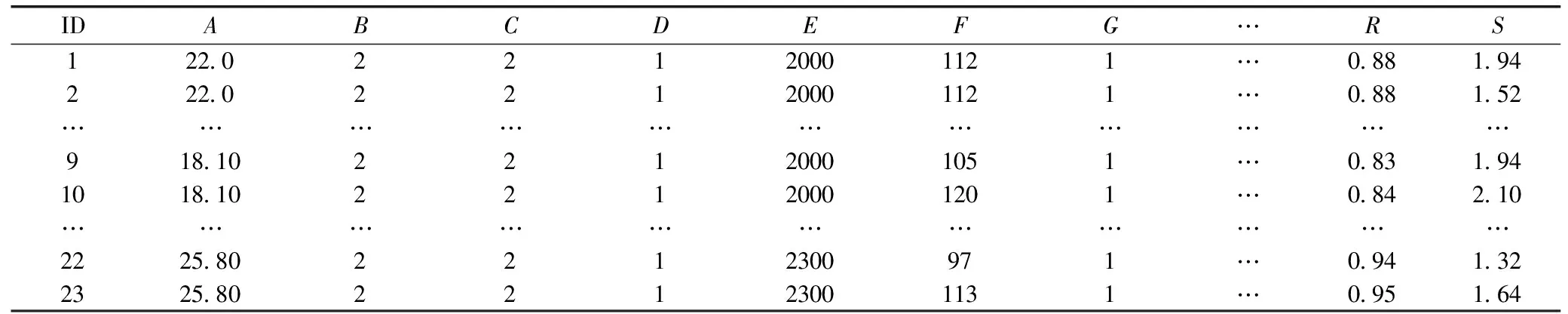
表5 顾北煤矿部分实测爆破数据

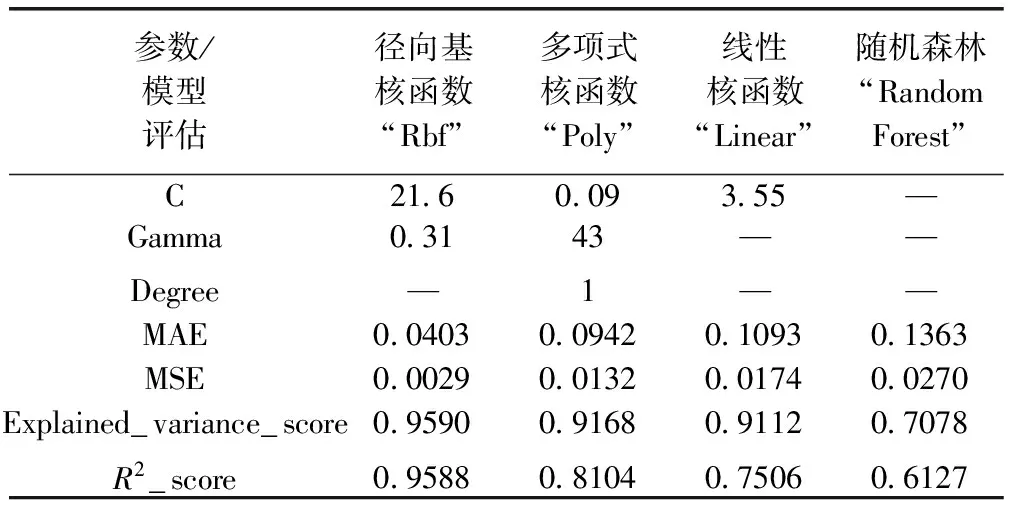
表6 顾北煤矿案例炸药单耗回归预测结果对比

参与预测的共计99组数据，训练集比重为0.768，预测集比重为0.232。

通过以上的参数和图像可以看到同样是SVR-Rbf组在各方面相较于其他三组有很大的优势，其相关系数为0.959，平均绝对误差也只有0.040，由此可见SVR-Rbf函数的确具有较强的实用性。另外两组SVR的函数表现不如Rbf。最重要的是，虽然预测出的数值有所差异，但是SVR的三种函数在图10中的预测趋势大致相同，说明SVR所搭载的函数有共通性，但径向基核函数表现更好，随机森林预测的表现依然不佳，印证了SVM算法更适用于小样本、高维度的数据的结论。

对所得数据进行进一步分析，分别绘制四种函数的误差直方图，依然同上一节的结论，SVR-Rbf组的误差范围最小，误差接近0的组别最多，而Poly和Linear组都是预测偏大；Rbf组的核密度值也是最大，且核密度值的峰值远高于其它组别，综合来看SVR-Rbf组预测效果最好。

本节介绍了以爆破数据库自己为训练集，实际案例为预测集的预测中，用支持向量机理论来预测炸药单耗展现出了非常好的预测能力，对实际案例具有良好的适应性。

4 结 论

1)提出了基于改进SVM算法的爆破效果预测方法。利用随机森林特征重要性方法获得了爆破效果影响因素的权重，并根据专家经验确定了6个关键指标，为提升爆破效果预测模型的准确性提供了前提条件。

2)针对岩石巷道爆破效果预测工程特点，构建了以平均绝对误差和相关系数为评价指标的网格搜索法-支持向量机回归爆破效果预测模型，基于径向基、多项式和线性三种支持向量机核函数对收集的76组样本进行预测训练，预测结果显示，SVR-Rbf函数预测的各项指标均优于其他函数，其中判定系数为0.935，平均绝对误差为0.129，SVR-Poly函数次之，SVR-Linear函数和Random Forest函数结果相似，表现最差。

3)为验证本文建立的爆破效果预测模型的可靠性，将模型应用于顾北煤矿实际工程中，以该矿实测23组数据作为测试集进行爆破效果预测，结果显示SVR-Rbf函数表现最佳，其判定系数为0.959，平均绝对误差为0.040，预测结果与实际相符。工程实际应用效果表明，本文提出的岩石巷道爆破效果预测方法具有较好的可靠性和实用性。