基于模糊时间知识推理的到发线运用冲突预测

冯丽萍，张立东，高 佳

（1.山东交通学院 轨道交通学院，山东 济南 250357；2. 山东交通学院 交通与物流工程学院，山东 济南 250357)

0 引言

到发线运用方案是涉及车站固定资源调配、车站列车到发顺序、特殊使用要求等限制的综合性方案，是保证列车能够正点、安全接发的关键技术文件之一。在使用过程中，往往由于列车运行受到干扰造成晚点导致实际使用方案偏离计划，继而需要对到发线运用方案进行调整。传统的到发线运用方案调整多在计划已经发生偏离后进行，且假定后续不会再发生其他扰动事件，导致到发线运用调整前提假设过于绝对，到发线运用调整弹性不足。因此，如何科学合理地丰富到发线运用方案调整决策信息，对提高到发线运用方案调整与优化水平具有重要意义。

目前针对到发线运用方案的研究主要集中在方案优化与动态调整2个方面。任禹谋等[1-2]以到发线均衡利用为优化目标，构建咽喉区和到发线整体运用优化模型，并以列车晚点总时长最小为目标，引入滚动时域调度策略，建立高速铁路车站到发线动态调整模型；霍亮[3]以咽喉道岔、到发线运用效率最大化和调机出段作业接续时间最少、走行距离最短为目标，对铁路客运站调机运用与列车接发进路进行了协同优化；朗越等[4]以均衡到发线设备时空应用和提高车站作业计划的稳定性为目标，提出列车进路链式分配模型；针对列车到发不确定性，李涛等[5-6]利用数理统计方法确定列车到发时刻的波动分布，并以列车占用到发线时间最小和到发线运用最均衡为优化目标建立客运站到发线运用优化模型；金福才等[7]将列车运行调整中的冲突判定转化为区间、车站和到发线3类，并引入堆栈方法对到发线冲突进行判定；廉志斌等[8]以所有列车的连带晚点时间之和最少、所有列车实际占用到发线偏离原计划程度最小为目标构建到发线运用计划调整模型并设计求解算法；潘明轩等[9]通过仿真实验分析了到发线运用对到达时间间隔的影响，并以最小总运营时间为目标建立优化模型，有效提高车站接发作业效率及通过能力。这些研究虽涉及列车到发不确定性的处理，但是优化调整的决策过程多局限在当前时间段，对未来一段时间内的到发线运用情况未予考虑。

研究通过模糊时间知识推理，将模糊弹性处理后的到发线运用方案在未来一段时间内的冲突进行定位和量化，可反馈用于当前的调整决策。拟通过整合周期性统计数据，模糊化处理到发线运用过程中的时间要素，通过构建到发线运用方案Petri网模型，基于模糊时间知识推理算法定位列车到发冲突位置并量化冲突可能性，为到发线运用方案调整奠定决策基础。

1 到发线运用方案建模

1.1 运用方案约束条件

到发线作业过程可以分为咽喉区占用作业和到发线占用作业2部分。到发线运用方案解决的是列车到发所需的咽喉区道岔、到发线的空间设备资源分配和列车占用到发线的时间分配问题。因此，到发线运用方案的制定受到时空约束如下。

（1）时间约束包括列车到发作业时间标准和相邻列车到发间的最小时间间隔约束。前者是指列车进行到发作业过程所需的最小时间，后者是指包括车站间隔时间和追踪间隔时间的列车间隔时间。

（2）空间约束是指由于车站设备资源的有限性和独占性，导致的列车对各项设备资源的占用不能同时进行且同一设备资源不能同时被一列以上的列车同时占用。

对到发线运用方案的时空约束形式化定义如下。假定某车站计划内共到发m列列车，车站内包括咽喉道岔组和到发线的设备资源n项，任一列车i在车站的到发过程中对任一设备资源j的占用关系xij需要满足以下约束条件。当第i列列车占用第j项设备资源时，xij取1，否则取0。

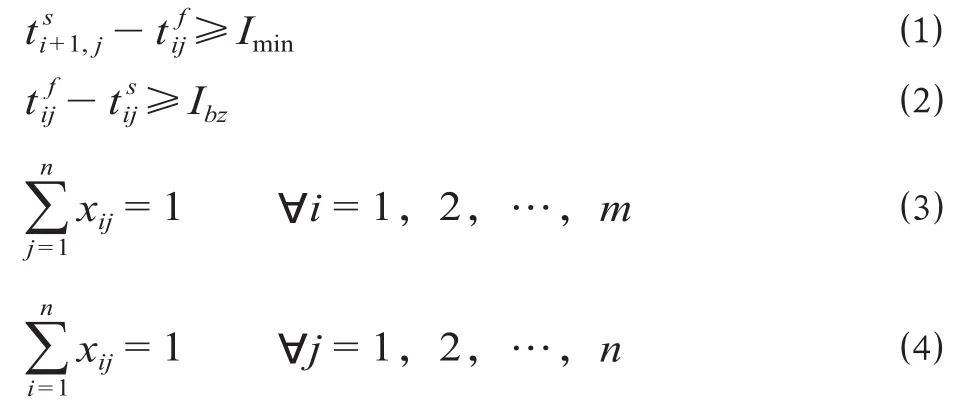
1.2 基于Petri网的运用方案建模

Petri网自1962年由C.A.Petri提出以来，以其简单的图形化表示和严密的数学理论支撑，尤其是在描述系统顺序、并发、冲突、异步等事件发生关系上的优势，被广泛应用于典型的铁路运输问题。考虑到到发线运用方案中的约束关系，建立包括M个库所和N个变迁的到发线运用方案Petri网形式化模型N如下。

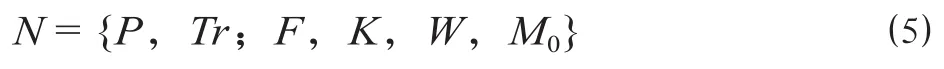
式中：P= {p1，p2，…，pM}为模型中的库所集合，根据库所标识表达到发线运用方案模型中列车位置、设备资源处于占用或者空闲的状态，此外还存在部分没有实际含义的逻辑库所，用以表达变迁间触发的逻辑关系；Tr= {tr1，tr2，…，trN}为模型中的变迁集合，用以表示到发线运用方案使用中的列车对设备资源的占用与释放；F为模型中的库所与变迁间的流关系，用以描述列车对设备资源动作的约束条件与后续影响；K，W分别为模型中库所的容量函数和流关系的权函数，且满足K=W= 1；M0为模型的初始标识，表示当前所有列车对所有设备资源的占用或释放状态。

基于到发线运用方案模型的形式化定义，建立到发线运用方案模型的具体步骤如下。

（1）考虑每列列车在该站的到发作业过程，建立初始Petri网模型。单列车作业模型如图1所示。其中，p1至p5分别代表列车到达站外、列车占用进站道岔组、列车占用到发线、列车占用出站道岔组和列车出站5种状态，Tr1至Tr4分别代表列车占用进站道岔组、列车占用到发线、列车占用出站道岔组、列车出站4种事件。需要特别说明的是为了叙述的方便仅考虑了进出站各1个道岔组，在实际建模中需按照列车对道岔组的占用顺序，依次添加库所和变迁。

图1 单列车作业模型Fig.1 Workflow model of a signal train

（2）考虑到发线运用方案中多列列车对同一个道岔组、同一条到发线在不同时间的计划占用关系，增加模型空间约束。增加空间约束模型如图2所示。其中，p6至p10，Tr5至Tr8的定义与图1类似，为另一列列车的到发作业过程模型，p11为到发线约束逻辑库所，根据到发线运用方案的形式化模型，库所内含有唯一托肯，表示2列列车对1条到发线的资源竞争关系。

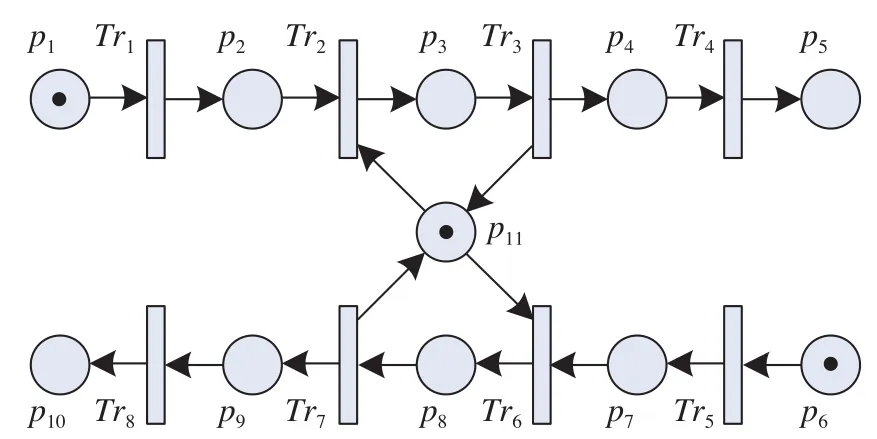
图2 增加空间约束模型Fig.2 Model with spatial constraint

（3）考虑相邻列车在该站的到发作业间的列车间隔时间，在空间约束模型的基础上增加模型时间约束，构建完整到发线运用方案模型。运用方案模型示例如图3所示，p12为2列列车作业顺序关系，根据图3中的流关系，下层列车出站道岔组占用变迁Tr8触发完成后才有可能触发上层列车进站道岔组占用变迁Tr1，即下层列车出发作业在前，上层列车进站作业在后。

图3 运用方案模型示例Fig.3 Model example of the operation plan

2 时间模糊化处理与推理算法

2.1 时间模糊化处理

在计划列车运行图中，设列车在车站到发线的停留时间为T= (b，c)，其中c为图定停站时间，min；b为最小停站时间，min；r= (c-b)为图定冗余时间，min。当列车在该站通过时，其在到发线上的停留时间可表示为(0，0)。考虑计划列车运行图使用的周期特性，以b，c为对比值，统计车站在1个周期内的到发列车实际停留时间，分别计算停留时间左偏(小于b)期望值E(Tb)和右偏(大于c)期望值E(Tc)，即可得到该站到发线停留时间的梯形模糊数如下。

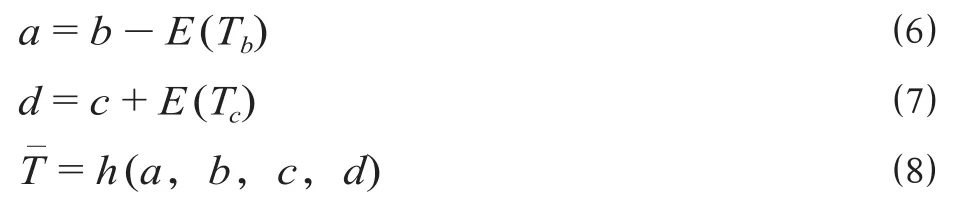
其中，h= 1，表示取值可能性的最大值，以上所有时间要素均为时间段。

同理，可对车站各到发线的进站道岔组占用时间及出站道岔组占用时间进行模糊化处理得到相应的梯形模糊数。

2.2 冲突判定条件与评价

列车到发线运用冲突是指相邻列车对同一设备资源(即进站道岔组、到发线、出站道岔组)占用的时间间隔不满足最小时间间隔的约束，即

时间模糊化处理后，列车对设备资源的占用时间为梯形模糊数。冲突判定示意图如图4所示，设前行列车梯形模糊数为T1=h(A，B，C，D)，后行列车梯形模糊数为T2=h(E，F，G，H)，其冲突判定为后行列车的最早开始时间E与前行列车最晚结束时间D的差值，即

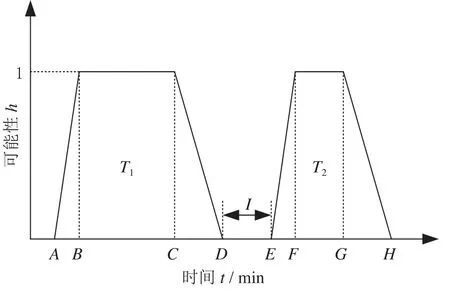
图4 冲突判定示意图Fig.4 Conflict judgment

基于梯形模糊数的定义及冲突判定准则，相邻列车间对同一设备资源的占用冲突可能性可通过如下步骤获得。

（1）根据缓冲时间使用的紧前原则，利用T1中的冗余时间进行冲突消解。若T1中的冗余时间r1=C-B大于冲突消解所需时间R，则冲突完全消解，冲突发生可能性为0。否则，进入第（2）步。

（2）利用T2中的缓冲时间r2=G-R进一步消解冲突，若r1+r2≥R，则冲突完全消解，冲突发生可能性为0，否则，T1，T2间隔时间不满足最小时间间隔约束，进入第（3）步计算冲突发生可能性。

（3）冲突发生可能性计算的前提是r1，r2已全部用于消解冲突时间R。此时由于梯形T1，T2中冗余时间已为0，梯形T1中的B，C点重合为一点，同理梯形T2中的F，G点重合为一点。原有的梯形模糊数更新为T1=h(A'，B'(C')，D')，T2=h(E'，F'(G')，H')。以T1中D'为起点，以2事件最小间隔时间Imin为长度作辅助线与T2相交部分的阴影面积占T2总面积的比例即为冲突发生可能性。

冲突可能性求解示意图如图5所示。由于冲突的实际发生是在前后两事件的冗余时间全部消耗完成后依然小于最小时间间隔的要求，因此，T1，T2中的冗余时间为0，由梯形模糊数变为三角模糊数。T1，T2冲突可能性η12的计算公式为

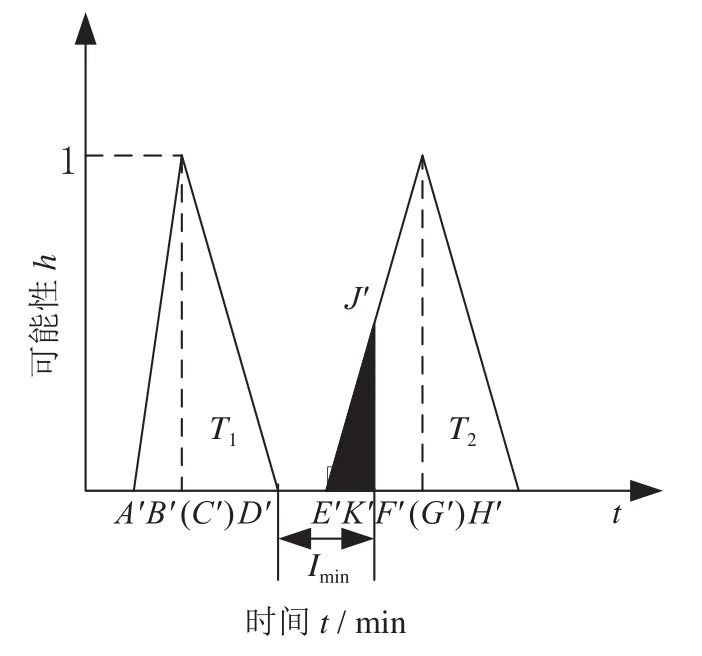
图5 冲突可能性求解示意图Fig.5 Conflict possibility solving

式中：S(E'K'J')为阴影部分面积；S(E'H'F')为更新后的三角模糊数T2面积。

2.3 到发线运用冲突推理算法

模糊时间知识推理算法在模糊时间Petri网中引入模糊时间片π(τ)、模糊使能时间e(τ)、模糊发生时间o(τ)和模糊延迟时间d(τ) 4个模糊集理论函数，基于最迟时间可能性分布函数latest、最早时间可能性分布函数earliest以及最小操作min运算方法，对以梯形模糊数表示的不确定时间进行推理。算法具体可参照文献[10]和文献[11]，现对4个模糊集理论函数概述如下。

（1）模糊延迟时间d(τ)。模糊延迟时间d(τ)是库所内托肯从到达到满足时间间隔约束条件所经历的时间长度可能性分布。令d(τ) =h1(a1，b1，c1，d1)，其中，b1为最短作业时间，c1为图定作业时间。

（2）模糊时间片π(τ)。模糊时间片是库所内托肯在时间τ时处于可用状态的可能性分布，即该库所达到了触发后集变迁的条件的可能性分布。同样令π(τ) =h2(a2，b2，c2，d2)，则

式中：o(τ) = (a4，b4，c4，d4)为变迁的模糊发生时间；⊕为加法算子。

（3）模糊使能时间e(τ)。模糊使能时间e(τ)是变迁t在时间τ时所有前集库所处于“有托肯”状态且可用的可能性分布。在到发线运用方案Petri网模型中，变迁的前集库所可能不止一个。根据Petri网的变迁使能条件，只有当所有前集库所中的托肯可用时，变迁才处于使能状态。因此，模糊使能时间e(τ)为前集库所中的最晚模糊时间片π(τ)，即

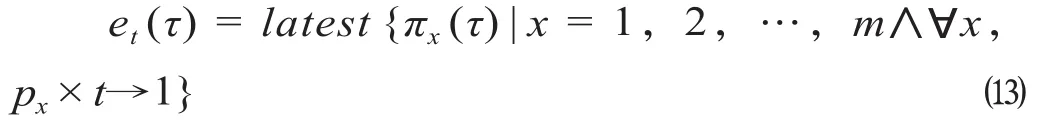
式中：πx(τ)为m个变迁t的前集库所的模糊时间片。

（4）模糊发生时间o(τ)。模糊发生时间o(τ)是指当多个变迁使能时，根据一定的决策策略确定该变迁在时间τ发生的可能性分布。决策策略根据实际情况可以选择“先到先服务”“后到先服务”等。本次研究采用“先到先服务”的服务策略，对较早使能的变迁赋予优先权。即

式中：ey(τ)为n个使能变迁的模糊使能时间。

基于模糊时间知识推理算法的到发线运用方案冲突预测步骤如下。①设置到发线运用方案Petri网模型初始标识，确定车站当前设备设施占用/空闲状态、列车位置信息。②自上而下、自左向右基于模糊时间知识推理算法推算变迁模糊发生时间o(τ)，依次对存在最小追踪间隔时间约束的前后列车进行冲突判定。若存在冲突，则计算冲突可能性η，并延后后行列车变迁发生时间以完全消解冲突，更新其模糊时间片。以图5中的冲突消解为例，将后行作业发生时间整体后移K'-E'，满足T1，T2间最小间隔约束。更新后T2的模糊发生时间为e(T2) = (K'，F'(G') + (K'-E')，H'+ (K'-E'))。若不存在冲突，则继续推理，直至遍历模型所有变迁。

3 算例

某单线横列式区段站部分布置图如图6所示，共有7条到发线，6组道岔。其中1号、II号、3号到发线为旅客列车到发线；4号、6号、7号到发线为货物列车到发线；道岔分组基于接发车进路与道岔的占用及妨碍关系确定。算例假定上行、下行各10列列车，其中旅客列车12列、货物列车8列。时间间隔约束I= 5 min。列车到发数据示例如表1所示。需要特别说明的是，虽然在本示例中，1号到发线、II号正线的占用不存在妨碍道岔组，但在实际应用中除直接占用的道岔组外，需考虑由于到发线使用过程中对妨碍道岔组的间接占用关系。该约束可参照前文到发线运用方案建模方法，补充模型中的资源占用时空约束关系即可。

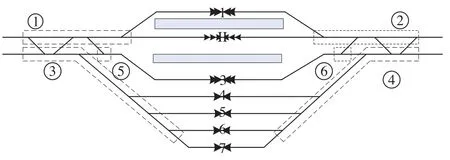
图6 单线横列式区段站部分布置图Fig.6 Layout of district station in horizontal type of single track railway

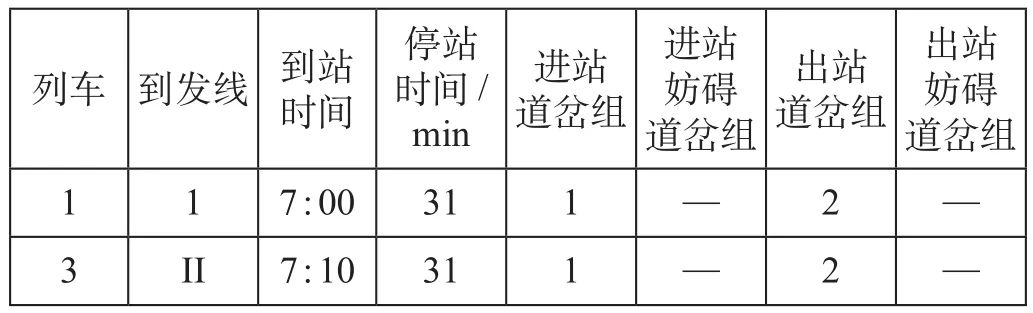
表1 列车到发数据示例Tab.1 Data example of train arrival and departure

假设将列车到发数据周期性统计处理，接发列车占用道岔组时间的模糊时间片设置如表2所示。除占用道岔组的模糊时间片处理外，列车停站时间中图定冗余时间r= 5 min，左偏3 min，右偏1 min。以列车1停站时间为例，其停站模糊时间片为(22，25，31，32)。其余相邻列车到发时间间隔模糊时间片中，图定冗余时间、左偏时间、右偏时间均为1 min。

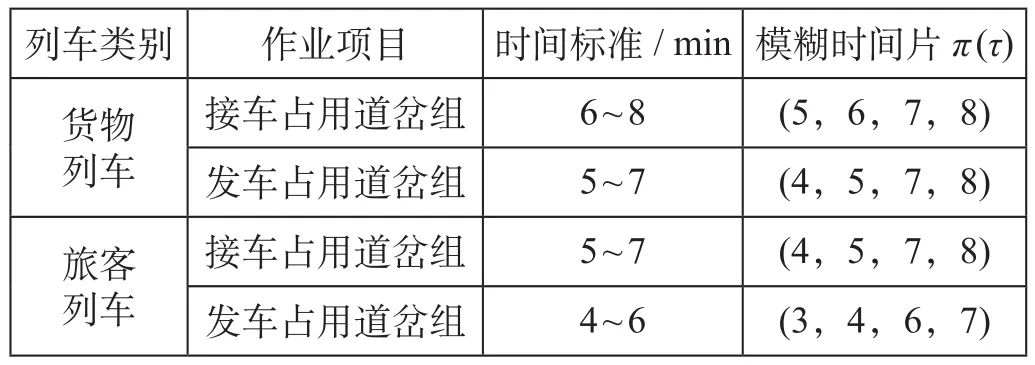
表2 模糊时间片设置Tab.2 Fuzzy time slice

运用前文中的基于Petri网的到发线运用方案建模方法，以表1中列车1和列车3为例，构建到发线运用方案模型如下。

在分别绘制2列列车作业模型的基础上，增加因2列车到发均需占用1号、2号道岔组产生的2个资源约束；最后考虑列车到发间的时间约束。列车1和列车3到发关系示意图如图7所示，存在列车1和列车3到达的追踪间隔约束IZD，列车3到达与列车1出发之间的不同时到发间隔约束IDF和列车1和列车3出发的追踪间隔约束IZF。

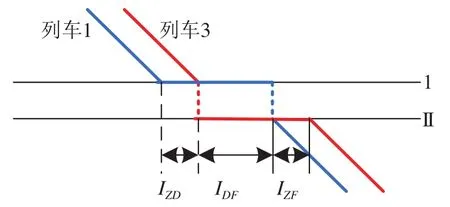
图7 列车1和列车3到发关系示意图Fig.7 Arrival-departure relationship between trains No. 1 and No. 3

综上，构建列车1和列车3到发线运用方案模型如图8所示。为增强模型的可读性，对模型中库所、变迁的命名规则规定如下：下标只有1位数字的表示列车序号；下标含有2位序号的表示列车对资源的占用关系；上标D表示列车到达站外、F表示列车出发进入区间、L表示占用到发线、DF表示到发时间间隔、ZD表示到达追踪间隔时间、ZF表示出发追踪间隔时间。

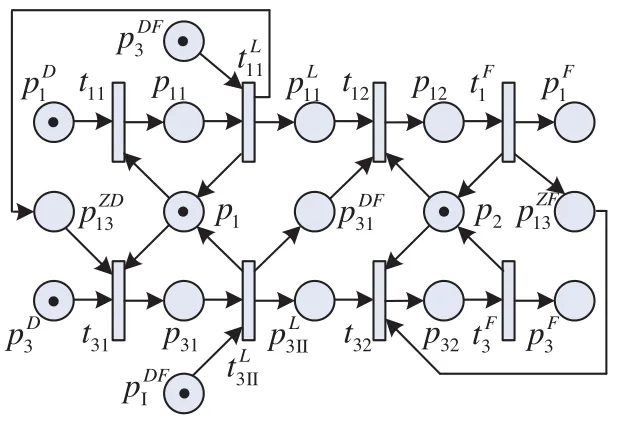
图8 列车1和列车3到发线运用方案模型Fig.8 Arrival-departure plan model of trains No. 1 and No. 3

模型构建完成后，以表示列车1占用进站道岔组1的变迁t11、表示列车1占用到发线的变迁表示列车3占用进站道岔组1的变迁t31，进行模糊时间知识推理，列车1和列车3到发模糊时间知识推理示例如表3所示。其中变迁与变迁t31之间存在冲突检查。

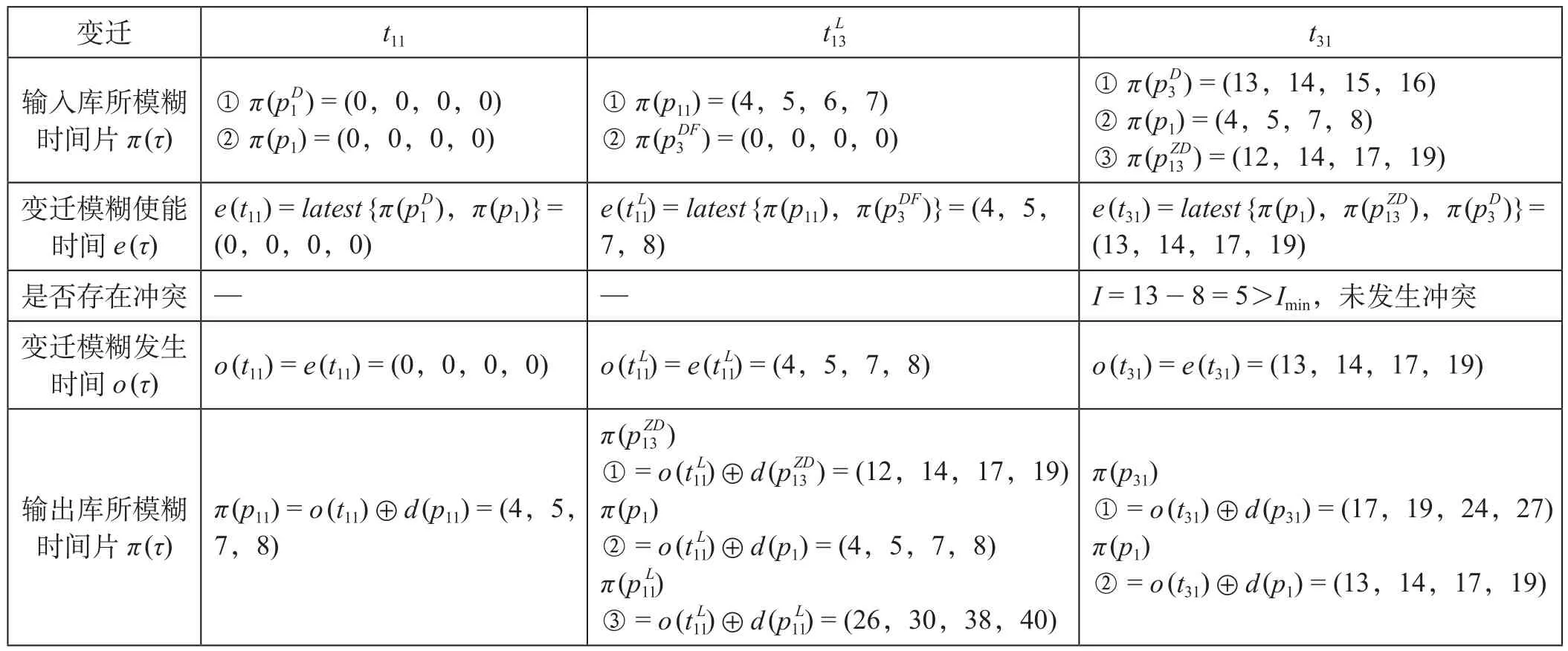
表3 列车1和列车3到发模糊时间知识推理示例Tab.3 Example of fuzzy temporal knowledge reasoning of arrival-departure relationship between train No. 1 and train No. 3

对算例中的20列列车的到发线运用方案构建Petri网模型，并基于模糊时间知识推理算法从上到下、从左到右进行推理，列车间冲突可能性示意图如图9所示。根据图9列车间冲突可能性计算结果得到冲突可能性分布如表4所示。通过模糊时间知识推理，可对到发线运用冲突产生的位置及可能性进行预判，为到发线运用方案调整奠定决策基础。

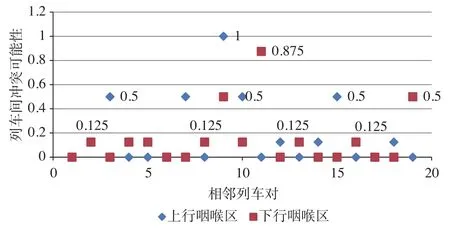
图9 列车间冲突可能性示意图Fig.9 Conflict possibility between trains

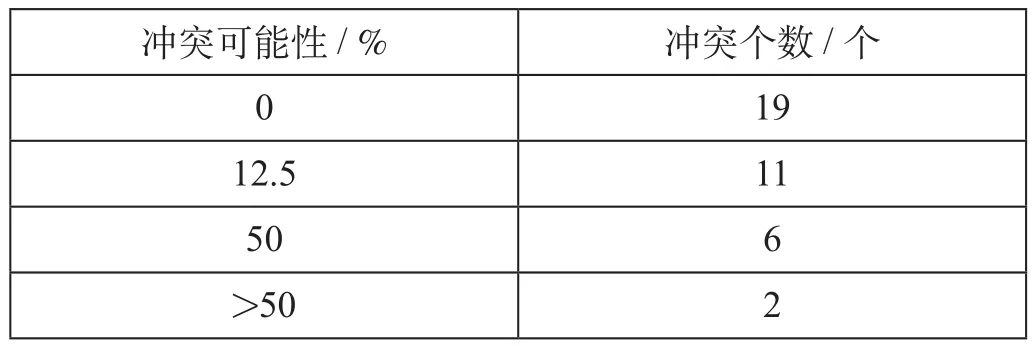
表4 冲突可能性分布Tab.4 Conflict possibility distribution

4 结论

研究通过将列车到发时间要素模糊化处理，提出基于模糊时间知识推理算法的到发线冲突预测算法，用以预判冲突发生位置及可能性，研究结论有以下几点。

（1）利用到发线运用计划周期性使用的统计数据，将运用方案中的时间要素从考虑冗余时间的区间数据模糊化为梯形模糊数，有利于丰富用于运用方案冲突预判的信息，并增强运用计划调整的弹性。

（2）基于Petri网的到发线运用方案建模，从单列车作业模型开始，依次增加资源约束、时间约束，流程逻辑清晰，可为后续基于编程语言实现面向对象的到发线运用方案建模提供思路。

（3）利用模糊时间知识推理算法，可实现对到发线运用方案中单列车到发偏离程度、列车间到发冲突发生的位置及可能性的预判，预判结果可为到发线运用计划调整奠定决策基础。

（4）由于晚点传播效应的影响，到发线运用方案的模糊时间知识推理存在越往后，冲突发生可能性越大，单列车偏离计划越多的现象。因此，推理到一定时间后，基于模糊时间知识推理的冲突预测不再有实际意义。下一步，可对停止模糊时间知识推理的阈值及基于模糊时间知识推理结果的冲突调整策略开展深入研究。