基于频率反馈锁相的双馈感应风力发电机频率稳定控制方法
唐升卫,李世明,胡春潮,刘菲,许良斐,顾礼斌
(1.广东电科院能源技术有限责任公司,广东 广州 510050;2.广东电网有限责任公司电力调度控制中心,广东广州 510030;3.北京四方继保自动化股份有限公司,北京 100085)
0 引言
双馈感应风机(DFIG-WT)和全功率直驱风机,均通过锁相环(PLL)与外界交流电网保持同步[1]。由于PLL具有快速响应能力,风机的输出电压能够快速追踪机端母线电压相角的变化,无法实现同步发电机内电势与机端电压矢量间的相对运动[2]。因此,风力发电机自身无法对外界系统的频率变化提供对应的输出功率响应,也无法参与系统的频率控制。
研究人员提出两类方法用于提升风力发电机的频率控制性能。第一类:模拟惯量控制(Synthetic Inertia Control,SIC),即在风力发电机的转速或转矩控制回路中,增加频率偏差的一阶微分,实现风机对系统频率扰动的响应[3]~[5]。系统频率偏差在经过一阶微分环节前,须要经过低通滤波器消除测量噪声和频率偏差中的高频分量。由于低通滤波器与一阶微分环节在通频带存在相互抵消现象,因此,SIC的参数选取必须通过精确的小干扰稳定性分析得到。SIC控制与风机本身的转速和转矩控制环紧密耦合,使得其动态性能受限于转速和转矩控制环的性能。第二类:在风力发电机的转速或转矩控制环中引入频率下垂控制,对系统的频率偏差进行控制[6],[7]。频率下垂控制的效果主要由下垂系数决定,下垂系数可影响风力发电机有功功率对系统单位频率偏差的响应幅度,频率下垂控制的效果同样受到风机的有功控制回路性能的限制[8]。
SIC控制和频率下垂控制方法均为简单、有效的风力发电机频率控制手段。但两种控制方法的响应速度和性能均受限于风力发电机控制系统的带宽。因此,本文利用SIC和下垂控制的简单、易实现优势,提出一种基于频率反馈锁相的频率稳定控制方法(Frequency Feedback Phase Locking,FFPL)。考虑到双馈感应风机已广泛应用在实际系统中,本文以双馈感应风力发电机为研究对象,以其频率稳定控制为目标,进行控制器设计和分析。本文所提出的FFPL控制方法直接作用于PLL的输出相角,可通过控制风机与电网接口电压矢量间的夹角而改变双馈风机的有功功率输出,因此FFPL可绕过双馈风机本身的内外环控制回路,提供更加快速的响应。FFPL综合了SIC、频率下垂控制的优势,具有结构简单、易实现特点。FFPL中引入系统频率偏差量的微分、比例和积分项,实现对系统频率的暂、稳态误差的响应,可适应于高比例可再生能源并网的电力系统频率控制。
1 FFPL控制器设计
1.1 双馈感应风力发电机结构及系统电压矢量运行原理
双馈感应风机主要由风塔、感应发电机(Doubly-Fed Induction Generator,DFIG)、转子侧换流器(RSC)、网侧换流器(GSC)及其控制系统组成。双馈风机最常用的控制系统为矢量控制系统,该系统主要由RSC控制器和GSC控制器组成。在矢量控制系统和坐标系的变换中,均须PLL测得的机端交流母线电压vabc的相角θPLL。在GSC控制器中,θPLL被用于控制器产生的dq轴参考控制电压到abc坐标系的变换,实现了GSC输出电压矢量与机端电压矢量间的同步。在RSC控制器中,θPLL-θr被用于控制器产生的dq轴参考控制电压到abc坐标系的变换,其中θr为发电机转子相角。通过上述电压矢量间的相位关系变换,实现了感应发电机定子绕组感应电势与机端电压矢量的同步,如图1所示。
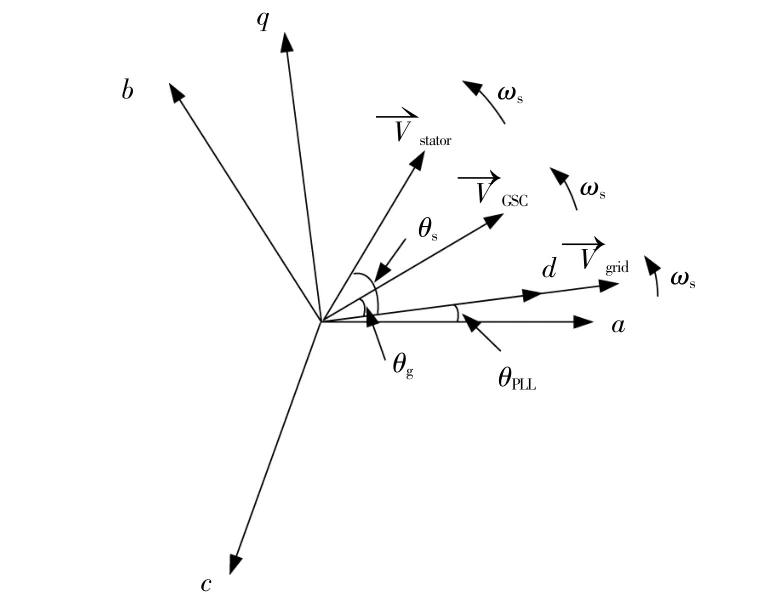
图1 双馈感应风力发电机各电压矢量的相位关系Fig.1 Spatial relationship of the voltage vectors of a DFIG-WT


1.2 频率反馈锁相控制器原理及其设计
现有研究中,SIC控制和频率下垂控制分别模仿同步发电机的惯性响应和一次调频功能。双馈风机模仿同步发电机对系统频率进行响应,实为双馈风机各电压矢量模仿同步发电机各电压矢量间的相对运动,如图2所示。
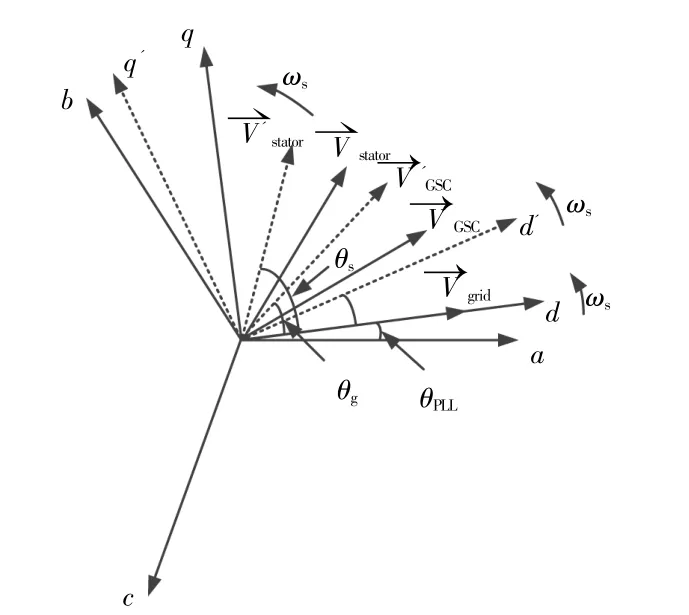
图2 含频率反馈锁相控制的双馈风机电压矢量相位关系Fig.2 Spatial relationship of voltage vectors of the DFIG-WT with the FFPL controller
若在系统频率受到扰动后,相应调整dq旋转坐标系d轴与abc静止坐标系的a轴间的夹角,即叠加Δθ于θPLL之上,则可改变θs和θg的值,使得Vstator移动到V′stator的位置,VGSCr移动到V′GSC的位置。相应的双馈风机定子侧输出有功和GSC输出有功功率会发生相应改变。
本文设计了FFPL控制器,如图3所示。
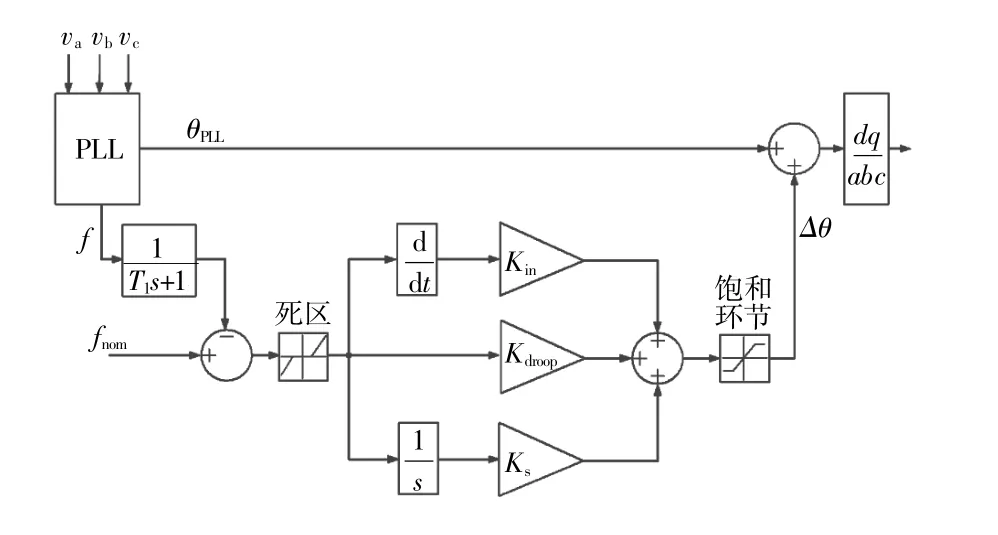
图3 频率反馈锁相控制器结构原理图Fig.3 Layout of the proposed FFPL controller

式中:Kin为微分环节增益,使FFPL提供与频率偏差一阶微分相关的输出分量;Kdroop为比例环节增益,使FFPL提供与频率偏差成比例的输出分量;Ks为积分环节增益,使FFPL提供与频率稳态偏差相关的输出分量。因此,FFPL在原理上可模拟包括惯性响应、一次调频和二次调频在内的频率控制过程。进而通过饱和环节对FFPL控制器的输出进行限幅,得到:

2 频率反馈锁相控制器参数设计与鲁棒性分析
本文所用双馈感应风力发电机模型参数如表1所示[9]。采用Matlab/Simulink中的线性分析工具对双馈风机系统进行根轨迹分析。FFPL控制器参数:Kin=0.01,Kdroop=0.2,Ks=3。以上参数依据线性分析工具中的最优化参数设计得到。
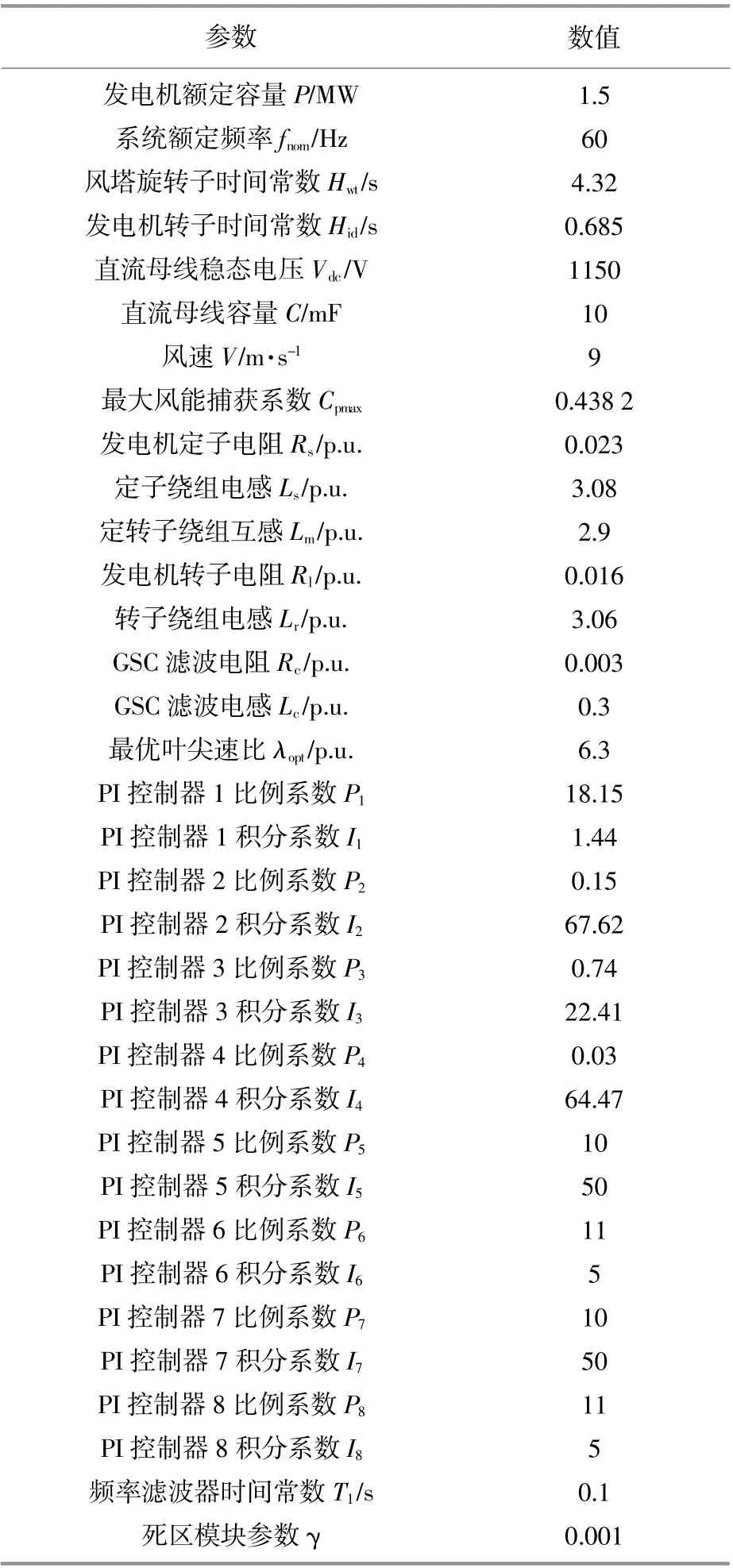
表1 双馈感应风力发电机参数Table 1 Parameters of the DFIG-WTs
2.1 频率反馈锁相控制器输出限幅设计
为了保证双馈风机系统运行的稳定性,FFPL控制器的输出须进行限幅,即为式(4)选取合适的φ+,φ-。令FFPL的输出Δθ由0 rad增加到0.5 rad,此时,双馈风机系统的极点迁移轨迹如图4所示。

图4 0 rad增加到0.5 rad时双馈风机系统极点迁移图Fig.4 Pole map of the DFIG-WT when the decreases from 0 rad to 0.5 rad
由图4可知,随着FFPL输出增加,系统极点的运动方向如图中箭头标注,可见系统的一对极点移动到右半复平面,其他极点则向左移动。为了保证系统稳定运行,所有极点均须在左半复平面,因此选取φ+=0.4 rad。
令FFPL的输出由0 rad减小到-0.5 rad,系统的极点迁移如图5所示。
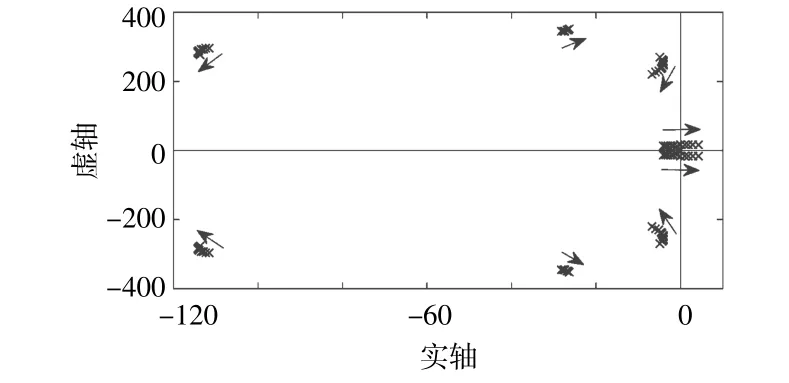
图5 0 rad减小到-0.5 rad时双馈风机系统极点迁移图Fig.5 Pole map of the DFIG-WT when the decreases from 0 rad to-0.5 rad
由图5可见,随着FFPL输出减小,系统的一对极点移动到右半复平面,其他极点则保持在左半复平面运动。同样为了保障系统的稳定性,须使系统的所有极点均在左半复平面。因此,FFPL输出的下界选取为φ-=-0.25 rad。
2.2 对控制器参数变化的鲁棒性
令转子转速控制环的PI控制器的比例和积分系数分别乘以矩阵[0.5,1.0,1.5],共得到9种P和I的组合。对应的系统极点如图6所示。
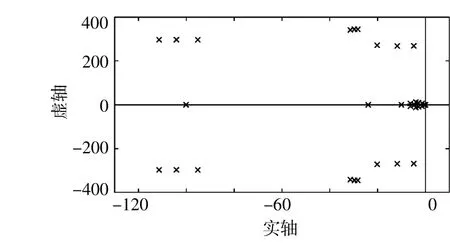
图6 FFPL控制下系统极点迁移情况Fig.6 Pole map of the DFIG-WT controlled by FFPL
在相同控制器参数下,绘制文献[4]所提出的SIC控制的双馈风机系统的极点,如图7所示。
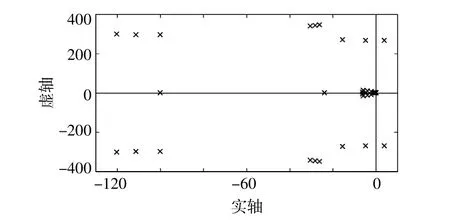
图7 SIC控制下系统极点迁移情况Fig.7 Pole map of the DFIG-WT controlled by SIC
由图6,7可知:在上述参数变化下,FFPL控制下双馈风机系统的极点均在左半复平面移动;SIC控制下系统的一对极点移动到了右半复平面,系统失稳。因此,本文所提出的FFPL控制方法在小干扰稳定指标下比SIC具有更优的鲁棒性。
3 时域仿真测试
本文的测试系统如图8所示[10]。
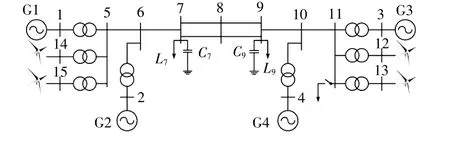
图8 测试系统拓扑结构图Fig.8 Schematic of the test power system
4个容量为75 MW的风力发电场分别连接于节点12,13,14,15,风电场动态用单台集中参数的双馈风机模拟,风机的参数如表1所示。同步发电机的初始出力相比于文献[10]系统分别降低93 MW,降低的出力由风力发电场提供。仿真分析在Matlab/Simulink中进行,测试条件的风速假定为15 m/s,风电场的稳态有功功率输出假定为0.6 2 p.u.。
在t=0.2 s时,节点11增加了150 MW负荷,系统频率受到扰动。图9为采用3种控制器配置下,系统频率与双馈风机相关的动态。由图9可知,前8 s,FFPL控制下系统频率振荡显著小于其他两种控制方法。这是由于FFPL控制下,双馈风机输出有功功率抬升远高于其他两种控制器。8 s后,系统中有功功率的生成和消耗的不平衡已得到很大缓解,此时系统的频率主要由同步发电机的行为决定,而3种控制器配置下,同步发电机的参数及固有振荡模态均相同。因此,8 s后,3种控制器控制下系统的频率振荡情况差别较小。
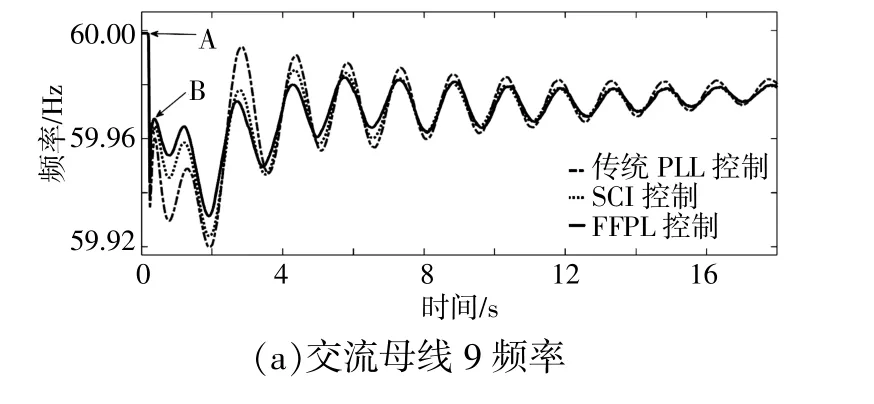
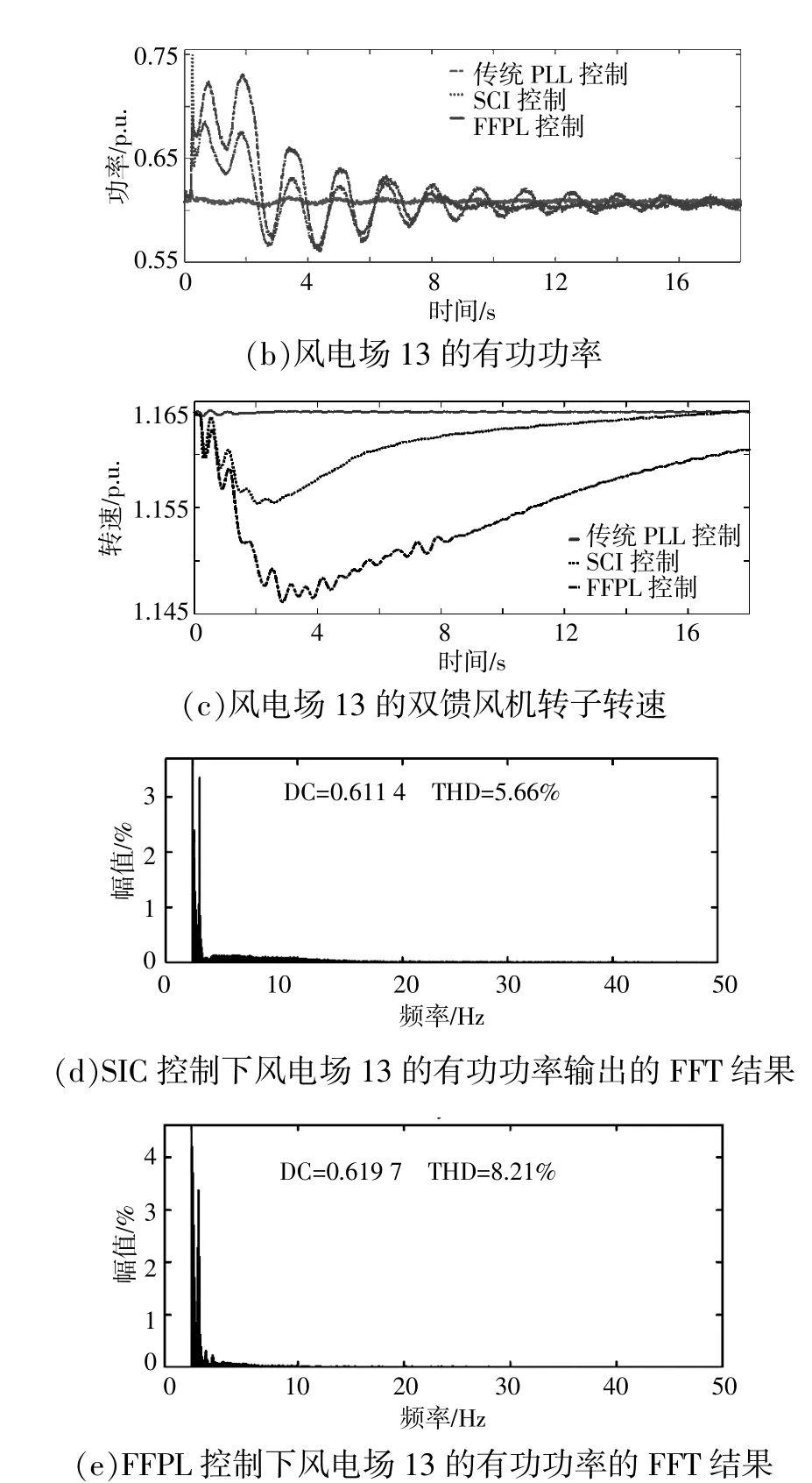
图9 系统发生负荷投运时,3种控制器配置下系统频率动态与风电场13中双馈风机动态Fig.9 System frequency and dynamics of the DFIG-WT in wind power plant 13 in the case where a load increase occurs in the system
FFPL控制下的双馈风机的输出功率增长最多,因而对系统频率的支撑也最强。采用矢量控制和传统PLL控制的系统,由于PLL对网侧交流母线矢量的精确追踪,双馈风机定子感应电势和GSC输出电压矢量与机端电压矢量间基本无相对运动,而双馈风机定子输出有功和GSC输出有功功率的变化主要取决于双馈风机定子感应电势和GSC输出电压矢量与机端电压矢量间夹角的变化,即图1中θs和θg的变化。但是由于PLL对网侧交流母线矢量的精确追踪,使得θs和θg的变化非常小,因而双馈风机定子有功输出和GSC有功输出均无明显变化,对外界系统频率变化无响应。仅采用矢量控制和常规PLL控制的风机有功出力基本无变化,与其运行原理相吻合。在FFPL控制下,风电场13的有功功率输出中直流分量为0.619 7 p.u.,高于SIC控制下风电场有功功率输出的直流分量0.611 4 p.u.,因而证明FFPL控制下,风机向外界交流电网提供更多有功功率支撑。同时,配置有FFPL控制的风机转子转速下降最多,原因是其有功出力增长最多,增长的有功功率本质上来源于转子释放的动能。因而,配置有FFPL控制的风机转子转速下降最多。
为了提供量化的比较结果,表2给出了3种控制器配置下,系统频率在负荷增加扰动后的变化率和受扰后系统频率的最小值,其中频率变化率由图9(a)中A点到B点的变化率得到。
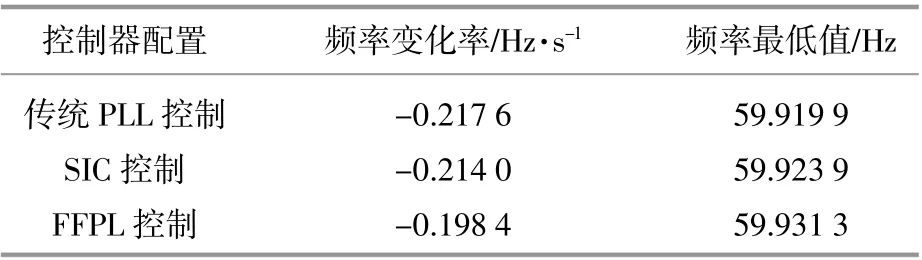
表2 系统频率受扰后的变化率和最小值Table 2 Rate of change of frequency and frequency nadir after the load increase disturbance
由表2可知,FFPL控制下,系统频率的变化率最小,即等效惯性最强。FFPL控制下的系统频率最小值最高,其对系统频率的支撑能力也最强。
4 试验验证
本文在环实验平台对SIC控制器的性能进行了测试,硬件在环实验平台由RTDS实时仿真器和dSPACE1006处理器构成,双馈感应风力发电机和外界电力系统由RTDS实时仿真器模拟,双馈风机的控制系统则由dSPACE处理器模拟,控制器与系统间通过GTAO板卡和光纤进行通讯。双馈风机和外界电力系统的建模和参数如文献[11]所示,双馈风机的额定容量为2 MV·A,稳态运行时风机的出力为1.2 MW。仿真环境如图10所示。在外界交流系统侧投入1 MW的负荷后,分别配置FFPL和SIC控制器的双馈感应风力发电机的响应如图11所示。
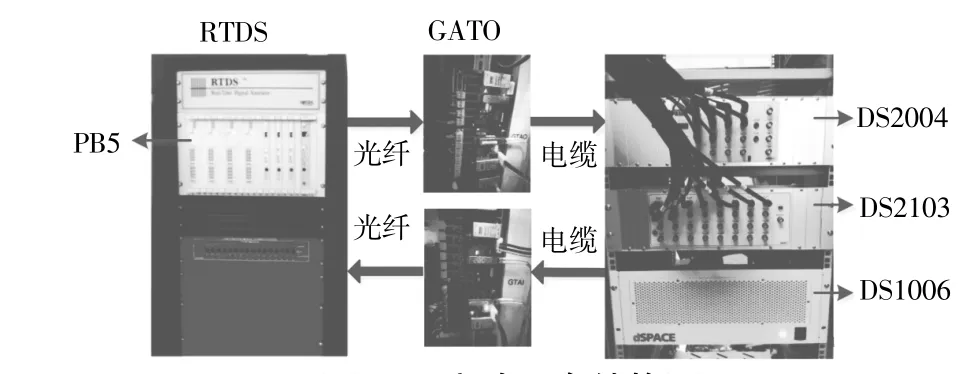
图10 实验平台结构图Fig.10 Layout of the experiment platform
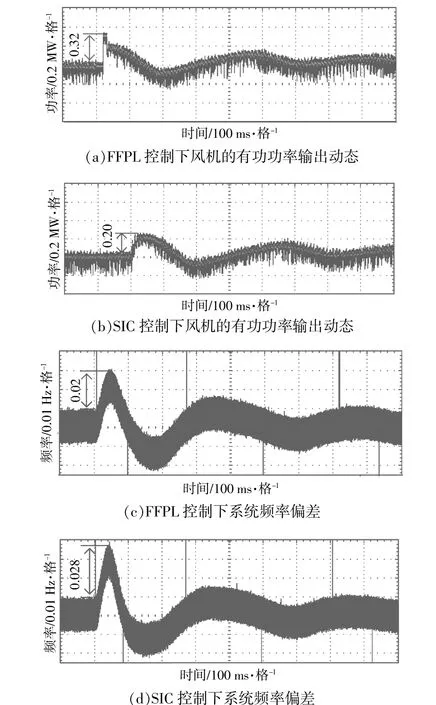
图11 双馈风机系统的频率响应比较Fig.11 Comparison of the frequency response of DFIG-WT controlled respectively
由图11可知,由于负荷突然增加,交流系统频率下降,在FFPL控制下双馈风机的有功功率输出增加。FFPL使双馈风机的有功输出增加0.32 MW以支撑交流系统频率恢复,对应的系统频率偏差fnom-f相对于额定频率下跌的最大幅值为0.02 Hz。在SIC控制下,双馈风机的有功功率输出增加的最大值为0.2 MW;相对于额定频率,系统频率下降的最大幅值为0.028 Hz。由此可见,在FFPL控制下双馈风机可以为外界交流系统提供更多有功功率支撑,使得系统频率的最大跌落得以缓解。
5 结束语
本文提出的FFPL控制算法,具有结构简单、易实现的优势,且根据根轨迹分析结果可知,与SIC控制相比,FFPL对控制系统参数变化具有更强的鲁棒性;由时域仿真和硬件在环试验结果可知,在FFPL控制下,双馈风机可为外界电力系统提供更快、更多的有功功率支持,使系统表现出更高的惯性且系统频率的最低点得到更多抬升。因此,本文所提出的FFPL控制的双馈风机,具有模拟同步发电机频率控制的能力,可提升含风力发电并网的电力系统的频率稳定性。

