重载VLCC的横向变速性能与靠泊速度控制

刘艳军 柴志文

一、引言

在船舶发展日益大型化、专业化的今天，20万t级及以上的VLCC被不断投入航运市场。和其他类型商船相比，这类船舶具有满载排水量大，对拖轮力、风压力作用不敏感等特点。在实践中，为了确保顺利地操纵重载VLCC靠泊，驾引人员不仅应选择在平潮期作业，还应采用合理的靠泊方式。为此，贾小堂[1]着重论述了30万t级油轮的进港控速时机；黎造邦[2]借助MATLAB软件全面分析了VLCC的操纵性能，并深入探讨了拖轮的使用方法；李培年[3]定性探讨了控制VLCC的进港速度和靠泊速度的方法。在可查阅的这些文献中，或偏重理论研究，或侧重定性讨论，而依据具体的船舶运动参数探讨控制VLCC靠泊速度的资料却很少。在操纵VLCC靠泊期间，引航员只能凭经验控制VLCC的靠泊速度，这难免会导致其心理压力较重，在指挥拖轮时频繁下口令，时而令拖轮顶推，时而令拖轮吊拖，更有甚者可能会忘记已发出的指令。本文基于重载VLCC的横向变速性能，结合当下作业环境和条件以及拖轮的输出功率提出合理的控速方式，并估算出合理的控速时机，为驾引人员操纵VLCC靠泊提供理论依据。

二、VLCC横向受力概述

操纵VLCC入泊程序复杂，在此过程中VLCC在水平方向上会受风压力、水阻力和拖轮力作用。其中，水阻力随船舶运动状态变化而变化，而拖轮力的大小及作用方向则取决于操船者的意愿。

（一）风压力

由于大多数港口对VLCC靠泊时的风力有明确规定（如天津港规定风力小于7级），且重载VLCC对横向风压的反应并不敏感，因此文中暂不探讨风压对重载VLCC横向靠泊操纵的影响。

（二）水阻力

在对水横移过程中，船体所受水阻力主要由摩擦阻力和压阻力构成。其中，压阻力所占比例远高于摩擦阻力所占的比例，因此可近似认为作用于横向运动船舶的水阻力等于压阻力[4]，即

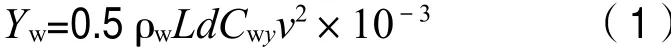
其中：Yw为水线以下船体所受的横向水阻力，N；ρw为海水密度，1 226 kg/m3；L为首尾柱间水线长度，m；d为平均吃水，m；Cwy为横向水动力系数；v为任意时刻船舶横向运动速度，m/s。

对于在特定环境中处于某装载状态的船舶来讲，除横移速度外，上述各参数均为定值；因此可视式（1）中的0.5ρwLdCwy为定值并称之为水阻力系数，用k表示，即

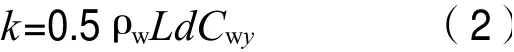
（三）拖轮的推力

在操纵大型船舶靠泊时，为确保安全靠泊并节省时间，操船者通常需要多艘大功率拖轮协助靠泊。据参考文献[5]，拖轮可发出的最大推力取决于主机额定输出功率及推进器类型。其中，最常见的ZP型港作拖轮每输出73.5 kW的功率可产生13.24～14.715 kN的推力，且当拖轮在开敞的环境中作业时，其做功效果随风力增大而变差。

三、船舶横向变速运动

据悉，各港口对于VLCC的入泊速度、入泊横距均有明确规定，如天津港规定：重载VLCC的纵向入泊速度应不超过1 kn，横向入泊横距应不小于3倍船宽。横向入泊运动，或经历加速运动、减速运动两个阶段，或经历加速运动、匀速运动、减速运动三个阶段。至于如何控制VLCC的横向运动速度，则主要取决于驾引人员的操纵习惯和拖轮的配置。

（一）VLCC的横向加速运动

考虑到在外力作用下重载VLCC的横向变速性能差，抵达泊位外档后，受双拖轮作用，VLCC的最大横移速度通常不超过40 cm/s，因此可认为作用于船体的压阻力系数为一定值。据牛顿第二定律可建立如下船舶加速横移运动方程[6]：

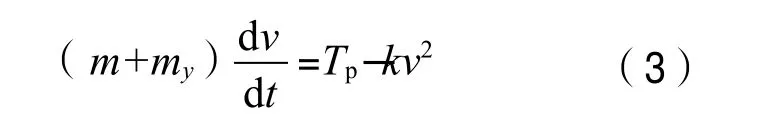
其中：m+my为船舶虚质量，kg；Tp为拖轮输出的推力，N。

解式（3）微分方程，得

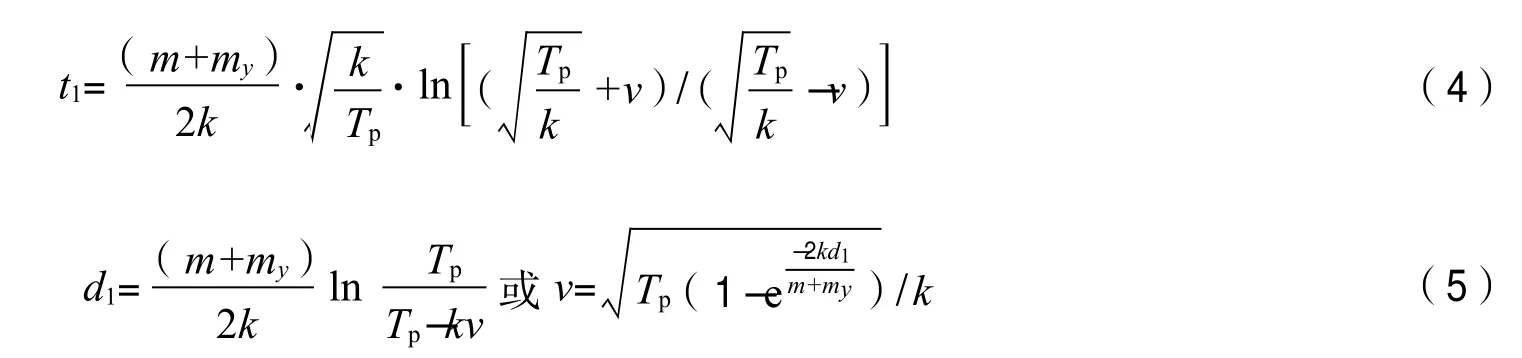
其中：t1为加速横移时间，s；d1为加速横移距离，m。

（二）VLCC的横向匀速运动

当作用于船体的拖轮推力和横向水阻力相等时，船舶将呈匀速横移运动状态。其运动方程为

式（6）可转变为

据此可断定，运动船舶所能达到的最大横移速度取决于拖轮的推力和水阻力系数。

（三）VLCC的横向漂移运动

当船舶横移速度达到某一值时，若令拖轮停止顶推作业，则船体在水平方向上仅受水阻力作用，船舶呈减速运动状态。其减速运动方程为

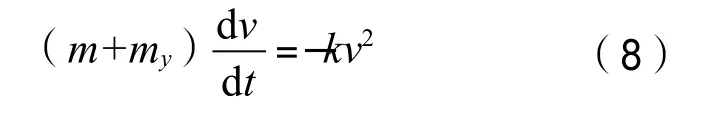
解此方程，得

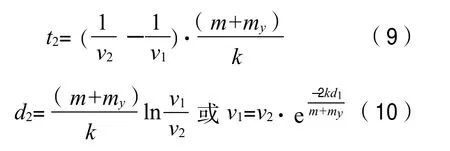
其中：t2为船舶漂移时间，s；d2为船舶漂移距离，m；v1为船舶运动的初速度，m/s；v2为船舶运动的末速度，m/s。

四、VLCC横向入泊速度的控制

从有利于安全操纵方面来讲，VLCC抵泊位外档后，合理控制船舶横移速度是确保VLCC安全靠岸的先决条件，为此需先确定控制横移速度的模式，再确定控速时机。

（一）控速模式的确定

（1）在实践中，为确保VLCC安全靠泊，人们通常取辅助拖轮额定输出功率的80%～90%为其常用功率。在操纵VLCC横向入泊过程中，为确保合理控制横向入泊速度，操船者首先应据拖轮的常用输出功率确定其常用推力Tp′，之后再通过式（7）根据VLCC的横向阻力系数k和拖轮的常用推力Tp′即可算出VLCC能够达到的最大横移速度vmax。

（2）在操纵VLCC横向入泊时，操船者期望的最佳运动模式是在拖轮的常用推力作用下，VLCC的横移速度达到某值之后，拖轮既不予顶推也不予吊拖，VLCC凭自身的惯性以适宜的横移速度靠岸。不妨假定：VLCC的初始横移速度为零；VLCC抵泊位外档时其距码头的横距为d，其值为船舶在加速横移阶段的横移距离d1与其在减速横移阶段的横移距离d2之和，如图1所示；拖轮的常用推力为Tp′；其靠岸速度为船舶运动的末速度d2。继而据上述条件建立下列方程式，并通过解该方程推导出所期望的船舶横移速度v′的表达式。

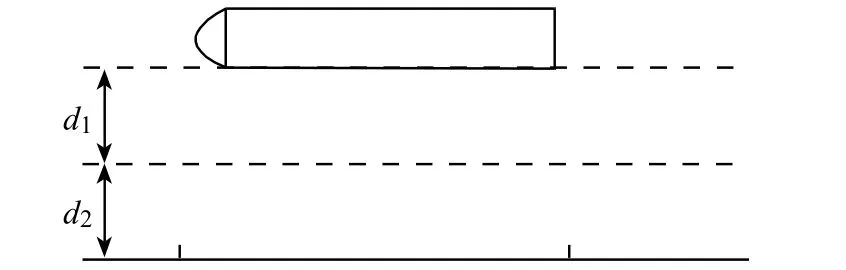
图1 船舶“两阶段式”横向运动距离

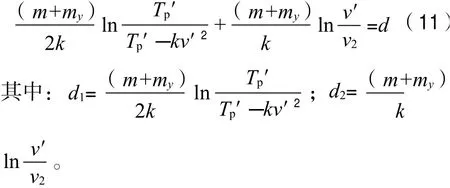
解式（11），得

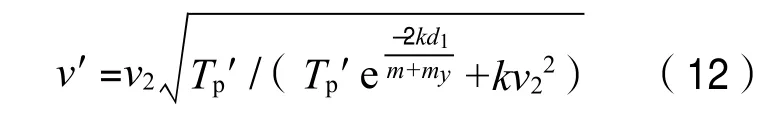
若v′≤vmax，则表明：承担顶推任务的拖轮所能发出的常用推力Tp′足以使VLCC的横移速度在合理期间达到预期值。据此可把整个横向入泊过程划分为加速运动和减速运动两个阶段，并把这种控速模式称为“两阶段”控速模式。

若v′≥vmax，则表明：① 操船者所企及的横移速度超出了拖轮推力的做功能力。②d的值过大，导致d2的值过大。换言之， VLCC的横移速度接近或达到峰值后，若令拖轮停止顶推，仅靠VLCC自身的惯性，VLCC会以远低于v2的理论速度靠岸。因此VLCC的横移速度达到vmax后仍需令拖轮持续顶推船体并使其横移若干距离，将这种控速模式称为“三阶段”控速模式。

（二）减速时机的确定

若确定以“两阶段”控速模式靠泊，须令承担顶推任务的两拖轮从顶推开始到顶推结束始终以同一推力Tp′顶推船体。VLCC的横移速度达到预期值之际，就是开始操纵其降速的最佳时机；而与之相对应的操作则是令拖轮停止顶推。

若确定以“三阶段式”模式靠泊，需依据事先算出的VLCC所能达到的最高横移速度vmax的值，然后再把所求vmax的值代入式（5）算出VLCC在加速运动阶段的横移距离d1；再据已求得的横移速度vmax的值，算出VLCC在减速阶段的横移距离d2；最后据d1、d2的值算出VLCC在匀速横移阶段的运动距离dm，如图2所示。从理论上讲，VLCC匀速横移了dm之后就是开始操纵其横向入泊速度的时机。

图2 船舶“三阶段式”横向运动距离

五、VLCC横向入泊算例

某VLCC轮M，总长333 m，水线间长323 m，船宽58 m，满载平吃水22.723 m，总载重量307 284 t，满载排水量351 284 t，TPC172.3，方形系数0.812。2021年7月20日该轮抵天津港，抵港时的实际排水量300 972.4 t，处于平吃水状态，吃水19.80 m。

考虑到潮流对靠泊操纵的影响，港方安排该轮于2021年7月21日上午平潮期（10：30时—11：30时，平均潮高约3.6 m）靠泊天津新港S30泊位（栈桥式码头，附近海图水深21.5 m），并安排2艘额定功率均为4 410 kW的拖轮、3艘额定功率均为3 675 kW的港作拖轮协助靠泊。

鉴于多数引航员的靠泊操纵习惯，在本例中特指定2艘额定功率为4 410 kW的港作拖轮承担在横向入泊期间的顶推任务；因此需依据它们的常用输出功率（推力）确定控制横向入泊速度方式并制订相应的靠泊控速预案。

（一）横向运动参数的推算

为了能够确定合理的横向入泊、控速时机，在进港前除了必须据实际情况制订进港计划外，还需事先获取下列船舶横向运动参数：

（1）水阻力系数k的值。依据参考文献[2，5]，认定该轮在当时相对水深条件下的横向水动力系数Cwy为3.7，代入式（2）得k=1.2×107N/s2。

（2）横向惯性系数（m+my）/2k的值。为获取船舶横向运动时的附加质量，周昭明[7]根据井上图谱给出下列回归公式。据该公式可计算出船舶在水深充分的水中横向运动时的附加质量为

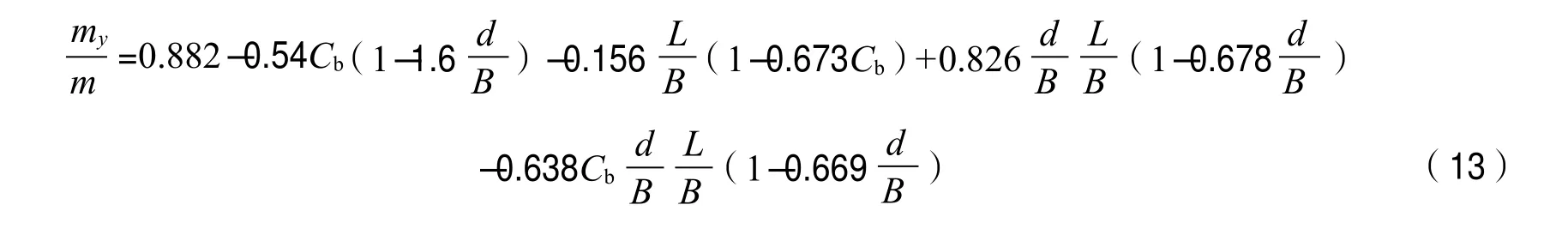
其中：d为船舶吃水，m；B为船宽，m；Cb为方形系数。

把相关数值带入式（13），可得my=0.736 m。考虑到当船舶在浅水中横向运动时，其附加质量会随水深变化而变化，为此可根据船舶附加质量浅水修正公式[8]计算出在浅水中船舶附加质量的变化倍率为

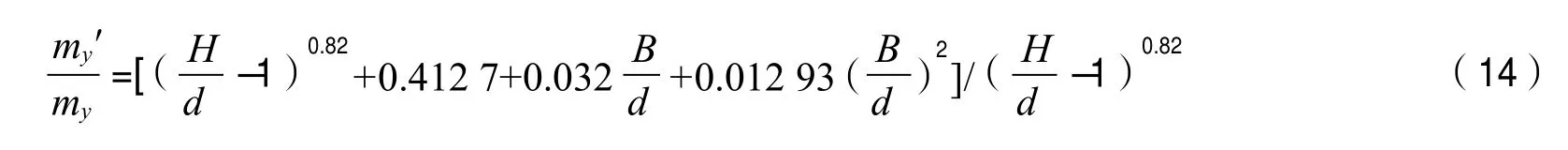
把相关数值代入式（14），得my′=1.8my。基于以上计算结果，可得（m+my）/2k为29.5 m。

（3）拖轮的额定推力Tp的值。据拖轮资料，用以顶推作业的单拖轮可产生的最大推力为882.9 kN。若把各拖轮额定功率的85%设定为最大常用输出功率，则在此条件下两拖轮发出的推力之和约为1 471.5 kN。

（二）最大横移速度的计算

假定该轮的横向入泊横距为180 m，把拖轮的最大常用推力值、船舶惯性系数、水阻力系数代入式（12）算出M轮的理想横移速度v′为33.34 cm/s，该速度即为预期速度。

由于v′≤vmax，因此采用“两阶段”控速模式和“三阶段”控速模式靠泊皆可。

（三）船舶横向运动距离及时间的计算

1.“两阶段”控速模式

（1）船舶横向加速运动：把所求速度值33 cm/s分别代入式（4）、（5），得到船舶横向加速运动的横移时间t1为293 s、横向加速运动的横移距离d1为63.8 m。

（2）船舶横向减速运动：把速度值33 cm/s分别代入式（9）、（10），得船舶漂移时间t2为989 s、漂移距离d1为110 m。

（3）计算结果表明：尽管所采纳的最大横移速度33 cm/s与理论上的最大横移速度33.34 cm/s仅差0.34 cm/s，该差值却可使加速运动距离减少5.3 m，加速运动时间减少16 s。反过来讲，若拖轮推力的实际做功效果不如拖轮的理论推力效果，则可能使M轮的加速运动距离大幅增大，这对后期的操纵是极为不利的。

2.“三阶段”控速模式

为了对比采用不同靠泊模式可能导致的不同结果，在此以初始靠泊横距为180 m、最大横移速度为25 cm/s为例，计算完成靠泊操作所需时间。

就移动互联网中存在的日益膨胀边界网关协议(BGP)路由表的问题，LISP架构设计了全新的网络结构来分离位置和标识。该架构的中心思想是将之前的IP地址分开终端的身份和位置信息，把IP地址在语义上划分成身份标识(EID)和位置标识(RLOC)两个空间。

将速度值25 cm/s分别代入式（4）、（5）、（9）、（10），可得船舶横向加速运动的横移时间t1为149 s、横移距离d1为20.8 m，船舶横向减速运动的横移时间t2为933 s、横移距离d2为93.8 m。进而可计算得出，船舶横向匀速运动的横移时间tm为262 s、横移距离dm为65.4 m。

综上所述，采用“两阶段”和“三阶段”模式靠泊所需时间分别为1 282 s和1 344 s，采用“两阶段”靠泊模式靠泊，比采用“三阶段”模式靠泊多耗时2 min。

（四）讨论与分析

（1）在船舶加速横移过程中，操船者不可能仅凭发给拖轮的指令预判其实际顶推效果。为此，需视式（5）为以横移距离d1为自变量的函数式，并绘制函数v（d1）的曲线图（如图3所示）和列表（如表1所示），据此可随时判断拖轮发出的推力是否适当。

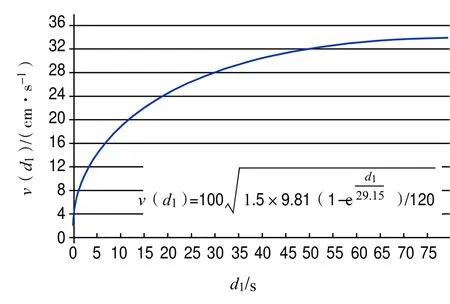
图3 横移速度随横移距离变化的曲线图

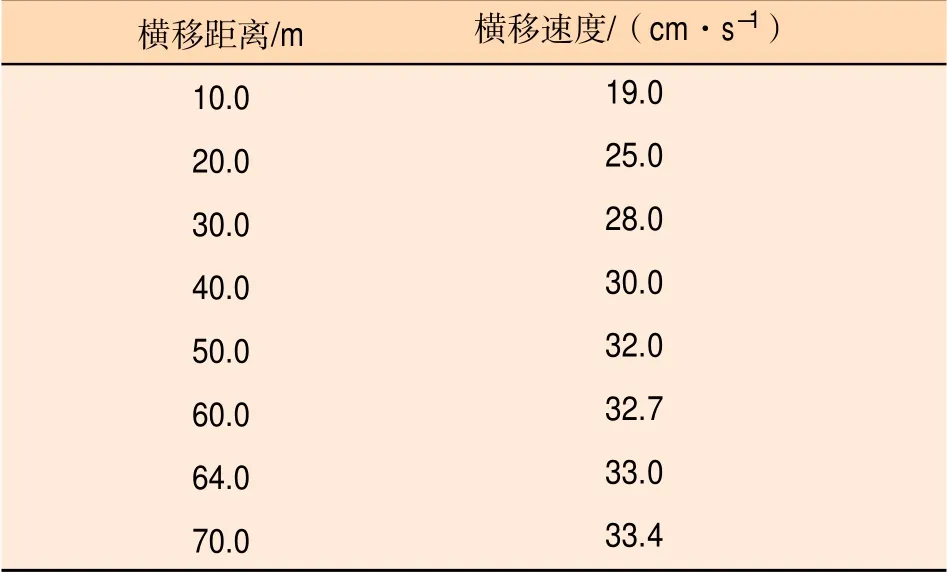
表1 横移速度随横移距离变化表

（2）在船舶减速横移过程中，操船者同样不能直接预判水阻力的降速效果；为此，应视式（10）为以d2为自变量的函数式，并事先绘制出函数v（d2）的曲线图（如图4所示）和列表（如表2所示），据此可随时核实水阻力的实际减速结果是否和表2所列横移速度值相符。

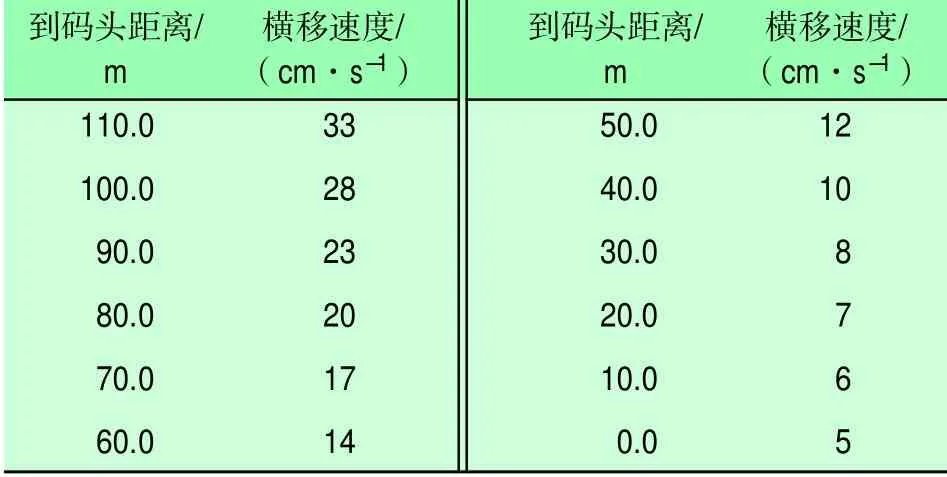
表2 横移速度随船舶距泊位距离变化表

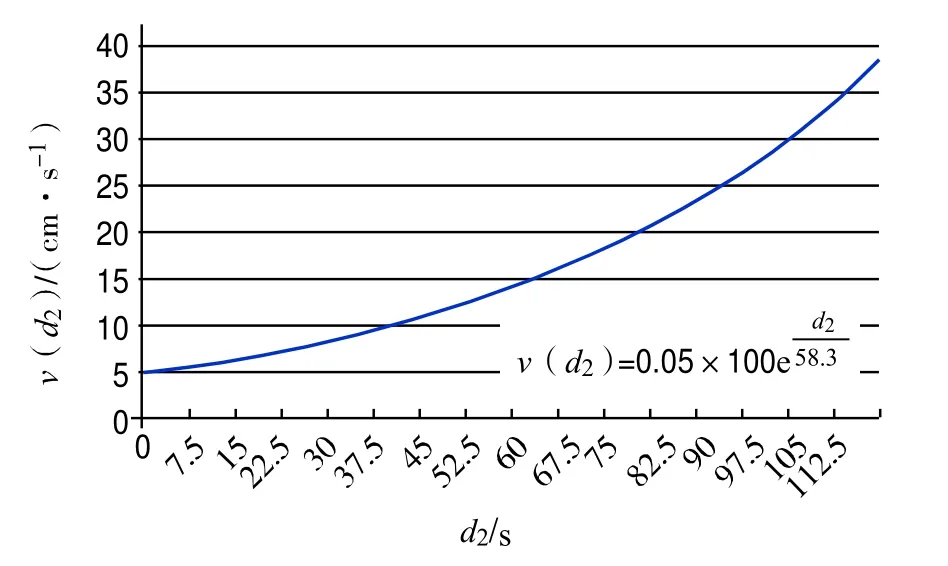
图4 横移速度随船舶到泊位距变化的曲线图

（3）就本算例而言，当M轮到泊位的距离小于10 m，且横移速度接近5 cm/s时，通过式（6）可求得前后两拖轮的最大许用推力之和，即Tp为30 kN。

六、横向入泊控速实例

M轮于2021年7月20日07：30时按计划进港靠S30泊位。当航行至距泊位约1.5 n mile处带妥4艘辅助拖轮。它们的配置顺序从前到后依次为津港轮15、津港轮28、津港轮29、津港轮19和津港轮20（如图5所示）。其中：津港轮15、津港轮18、津港轮19的额定输出功率为3 675 kW；津港轮28、津港轮29的额定输出功率为4 410 kW。当时风力偏北风2级，风压作用较弱，可忽略不计。

图5 拖轮配置

（一）入泊操纵实录

（1）10：07时，航速3.4kn，船首距泊位0.7 n mile，操纵M轮转向泊位。船舶操纵进入入泊阶段。

（2）10：35时，该轮抵泊位外档，距泊位距离如图6所示，船舶操纵进入入泊阶段。基于当时实际情况，并为验证算例中的船舶运动参数的可靠性，确定采用“两阶段”控速模式靠泊。具体操纵措施及相关船舶运动参数见表3所列。

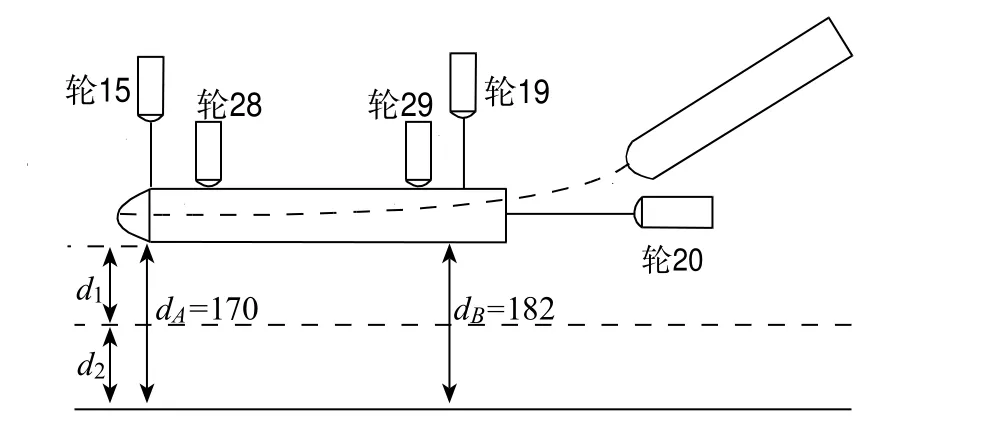
图6 船舶入泊示意图

表3 操纵措施及相关船舶运动参数

（3）10：57时，M轮以4 cm/s的速度平行靠岸。

（二）讨论与分析

表3所列的船舶变速运动数据表明，该表所列数值与理论计算结果相符。因此可断定：文中所引用的各运动参数是可靠的；在相同或相近的外界条件下操船者可直接引用这些参数。

（1）在加速拢泊的初期，M轮产生了向后运动的速度，究其原因极有可能是因津港轮28、津港轮29的顶推船舶角度出现了偏差，好在通过转舵、进车既抑制了船舶后退速度又调整了船首。

（2）10:49时，发现船首有向左偏转的趋势，随即令津港轮15慢速拖、津港轮29慢速顶，使船舶的偏转趋势得到抑制，究其原因很可能是因水下底土面不平所致。

（3）由于靠泊仪所显示的横移速度仅能精确到厘米级，且拖轮输出功率存在些许误差，和靠泊仪所显示的真实速度、横距相比，计算出的预期横移速度和横距必然存在误差。但在靠泊过程中引航员可依据靠泊控速预案及时予以纠正。

七、结束语

在电子信息技术高度发达的今天，在操纵超大型船舶横向入泊时，粗放型的入泊操纵方式已不符合时代要求。本文涉及的原理不难，但相关的数学运算却较为复杂，不过借助电脑软件、手机APP等相关电子计算工具可快速完成过去靠手工难以解决的数学运算。因此，只要在靠泊前做好相应的准备工作，就可在操纵VLCC横向入泊过程中避免盲目指挥拖轮。

天津港同仁的多次靠泊实践证明：文中给出的控制VLCC横向入泊速度的方法既可靠又实用；既适用于VLCC又适用于其他超大型船舶。希望兄弟港口的同仁们在引航实践中对本方法的可靠性予以佐证。