水文站渠道输水流量测验误差分析及优化设计

郑玉峰

（河北省唐山水文勘测研究中心，河北 唐山 064100）

流量是江河湖库水体变化的水文资料。为了掌握流量变化情况，要求在江河湖库设立的水文站，根据河流水情变化特点，采用合理的流量测验方案施测流量。我国在建的水库水文站都肩负着渠道输水水量的计量任务，严格执行《河流流量测验规范》（GB50179—2015）（以下简称《规范》），不断更新测验设施，逐步提高测验精度，圆满完成输水计量任务。为提高流量测验精度，水文站普遍采用流速仪多垂线多测点法施测流量，控制流速从水面到河底的不均匀分布。但是多垂线多测点施测方案测验误差是多少，测验精度达到何种水平，尚未进行深入的研究。随着《规范》颁布实施，其中明确了流量测验误差估算和施测方案优化的具体要求。依据《规范》，对水文站渠道输水流量测验误差给出了具体分析方法，以达到优化测流方案、提高测验精度的目的。

1 流量测验误差

流量测验存在的误差是指流量测量值与其真值之差，其产生是由流量测验方案的性质决定的。首先，流量的测量值是对计算公式中所采用的各种单项变量分别进行直接测量，在此基础上进行计算而得出的；其次，由于测量流量的不重复性，对某一时刻某一水流状态下的实测流量只能作一次测量，以测定相应各单项变量的值。流量测验误差是综合各单项变量测验误差的结果。

1.1 误差来源

采用流速仪法测流并用平均分割法计算流量时，误差来源于下述几个方面。

（1）起点距定位不准、水深测量方法不正确和流量测验过程中操作不当导致的误差，以及秒表未检定导致的计时误差。

（2）流速仪超期使用未检定、流向偏角超限和上游障碍物干扰水流等导致的误差。

（3）在流量测量断面的每条测速垂线上，对在水深不同位置上的测点流速、有限的测速历时引起的误差，即测点流速受脉动现象影响所产生的误差，在国际标准中称Ⅰ型误差。

（4）在流量测量断面的每条测速垂线上，在不同位置由于测点数目不足导致的垂线平均流速计算误差，在国际标准中称Ⅱ型误差。

（5）在流量测量中由于测速垂线数目不足导致的误差，即两垂线之间用内插方法来确定流速分布引起的误差，在国际标准中称Ⅲ型误差。

1.2 误差分类

流量测验误差按性质分为随机误差、系统误差和伪误差。

误差因来源不同具有不相同的性质。测深误差与测宽误差由观测的随机误差和仪器自身造成的未定系统误差组成；流速仪检定误差由仪器检定的随机误差和仪器自身在测量中所造成的未定系统误差组成；Ⅰ型误差为随机误差；Ⅱ型误差和Ⅲ型误差由随机误差和已定系统误差组成。

《规范》规定，随机误差按正态分布，采用置信水平为95%的随机不确定度描述；未定系统误差，采用置信水平不低于95%的系统不确定度描述；已定系统误差，应进行修正。

流量测验中的伪误差，即由于测验差错或人为粗心造成的明显歪曲测量结果的误差，在测量过程或数据处理中应尽可能地发现，含有伪误差的测量成果必须剔除。

2 流量测验误差试验

《规范》中流量测验精度所作的规定是依据我国南方湿润地区的10 余个水文站的流量测验误差试验和模型试验分析成果制定的。受自然条件和技术手段等因素限制，在我国干旱和半干旱地区尚未进行系统的流量测验各分量的误差试验。对于水文站这种人工渠道断面的流量测验误差，无试验成果可供借鉴，需要开展试验。

《规范》对不同测验精度类别水文站的各水位分级的误差试验给出了具体技术要求，首先要确定水文站的站类和水位分级，以便进行误差试验和估算测验误差。

2.1 测验精度类别和水位级的划分

渠道输水为水库出口站，肩负着输水计量任务，其流量测验精度高低直接关系到城市生活生产主要水源的科学调度和水资源的合理配置。测站任务的重要性决定了该站要达到较高的流量测验精度，因此确定渠道输水水文站为一类精度水文站。

由于输水渠道的流量受人为控制，不同于天然河道，各年最高水位相差不大，频率计算失去意义，无法采用年特征值法划分水位级。根据渠道的输水能力和各年输水流量的大小来划分高、中、低水位，更符合实际情况。

2.2 测验误差试验

流量测验误差试验工作根据《规范》要求和输水实际情况，按流量测验误差的来源分项进行。

测宽误差由缆道设备自身所决定，其起点距在测流缆道主索上，测速悬索可准确置于任一位置，误差能控制在规定范围内。由于断面及渠底高程无变化，每次施测流量均根据水位查算断面，其测深误差实际上由水位观读误差所决定。因此，测宽和测深误差不需要进行试验，主要是试验和估算流速测量的Ⅰ、Ⅱ、Ⅲ型误差。试验结合水文站原有的施测方案进行，增加测点和垂线，其布设位置应能反映测流断面流速分布的一般规律，垂线和测点的布设控制了流速分布的变化范围。

（1）Ⅰ型误差的试验应在水位稳定时进行。每次均取断面均匀分布的4 条垂线、2 个测点测量，测点测速历时2 000 s，每10 s 观测1 个流速，至少试验4次。

（2）Ⅱ型误差试验根据断面流速分布情况、每次均在包括中泓在内的6 条垂线上施测，每条垂线布设11个测点，测速历时60 s或100 s，至少试验20次。

（3）Ⅲ型误差试验在输水过程中进行，布设不少于11条垂线，用两点法施测，测速历时60 s或100 s，至少试验20次。

流速测量的Ⅰ、Ⅱ、Ⅲ型误差试验均在水流平稳、水位无涨落变化条件下进行，试验所用流速仪应为新检定的仪器，性能良好。整个试验过程中均应采用同一架仪器。试验人员按《规范》规定操作，所取得的数据能够满足分析计算的要求。

3 流量测验误差估算

流量实际测量值为一间接测量值，其误差是由各单项分量的误差综合而得到的。因此，估算流量测验误差首先要分别估算各有关分量的测量误差。水文站采用缆道流速仪法施测流量，缆道的定位精度使得测宽和测深误差控制在《规范》允许范围内，而流速仪检定误差由检定单位所决定，应在《规范》规定范围内，这里主要根据误差试验结果来估算流速测量的Ⅰ、Ⅱ、Ⅲ型误差。

3.1 Ⅰ型误差

Ⅰ型误差性质记述如下：随水深和垂线位置而变化；随流速而变化，一般是随流速减少而增大；随测速历时增加而减少。Ⅰ型误差是随机误差，采用置信水平为95%的随机不确定度来描述。

对Ⅰ型误差试验阶段取得的测速历时为10 s的原始流速测量系列进行整理，绘制流速脉动过程线发现伪误差和不稳定因素，并将其剔除。根据拉依达准则，对于某个残差大于测量系列3 倍标准差的测量值，认为含有伪误差，予以剔除。剔除坏值后的测量系列更具有代表性。

3.1.1 测点的Ⅰ型相对标准差估算

不同测速历时的测点Ⅰ型相对标准差，使用原始测量系列的标准差和自相关函数按下列公式估算：

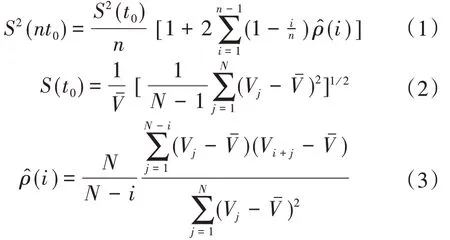
式中：t0为原始测量时段（s）；n为原始测量时段倍数；S（nt0）为测速历时为nt0的测点Ⅰ型相对标准差（%）；S（t0）为原始测量系列的相对标准差（%）为时段位移为i的原始测量系列的自相关函数；Vj为原始测量系列中第j个测点流速值（m/s）；Vi+j为原始测量系列中第i+j个测点流速值（m/s）为原始测量系列的算术平均值（m/s）；N为原始测量系列的样本容量。

采用置信水平为95%的随机不确定度描述Ⅰ型误差，即：

式中：X'e（nt0）为测速历时为nt0的测点Ⅰ型随机不确定度（%）。

3.1.2 垂线的Ⅰ型相对标准差估算

测速垂线平均流速的测量应采用有限测点和有限测速历时实际测量，得出垂线平均流速。流量计算规则造成的系统误差和由流速脉动造成的随机误差，后者即为垂线的Ⅰ型误差。对于垂线上的Ⅰ型相对标准差，根据垂线平均流速计算公式和误差的传递公式由测点计算到测速垂线上，其计算公式为：

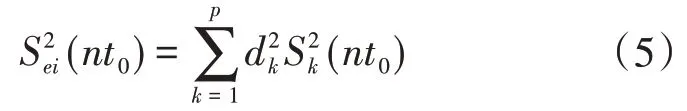
式中：Sei（nt0）为测点测速历时为nt0的第i条垂线的Ⅰ型相对标准差（%）；p为用以确定垂线平均流速的垂线测点数；dk为确定垂线平均流速时测点流速的权系数；Sk（nt0）为测点k处的测速历时为nt0的Ⅰ型相对标准差（%）。

3.1.3 断面的Ⅰ型相对标准差估算

断面的Ⅰ型相对标准差，按下式估算：

式中：Se（nt0）为测点测速历时为nt0时的断面Ⅰ型相对标准差（%）；m为用以确定单次流量Ⅰ型误差的测速垂线数。

3.2 Ⅱ型误差

测速垂线上的平均流速测量按规范采用有限测点进行施测，经过计算得到垂线平均流速，通常由于经过计算规则所造成的系统误差与随机误差，即为Ⅱ型误差。估算Ⅱ型误差，首先要对试验资料进行整理分析，确定垂线平均流速的真值和实际计算的垂线平均流速。采用11 点法计算的垂线平均流速作为其近似真值，将少点法计算的垂线平均流速除以近似真值，得到相对平均流速，采用下列公式估算Ⅱ型误差：

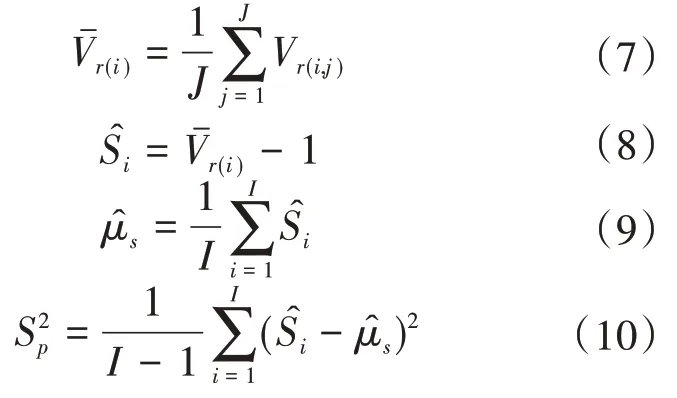
3.3 Ⅲ型误差

测流断面上的垂线数目数量是造成单次流量测验误差的主要因素，因此采用多垂线少测点的方法进行Ⅲ型误差试验，一般不少于10条垂线。对试验资料进行整理分析，按平均分割法计算流量，根据断面实际情况以11条垂线计算的流量作为近似真值。根据断面形状及流速横向分布特点，遵从水文站目前的垂线布设方法，将现有垂线作为保留垂线，按均匀抽取原则，精简一定数目的垂线，经计算得到少垂线法流量。即去掉2 条垂线，得到9 线法流量；继续去掉2 条垂线，得到7 线法流量；再去掉2 条垂线，得到5线法流量。从断面中抽去垂线，算得各次流量的近似真值和少线法流量，按下列公式估算Ⅲ型误差：

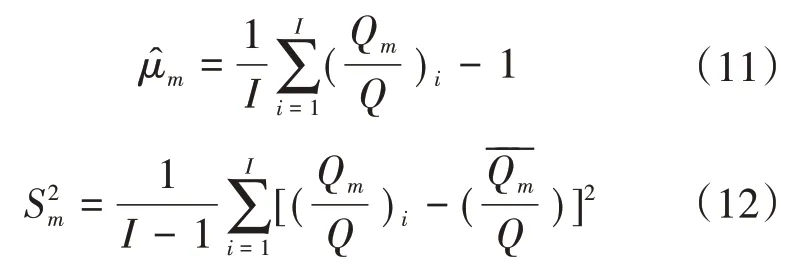
3.4 测宽、测深和流速仪检定误差

水文站流量测验设施一般为水文缆道，起点距最小刻度都能满足0.1 m，测宽的定位误差都能控制在0.1 m之内，按垂线间距不少于0.5 m计算，测宽的随机误差应控制在2%以内，并且无系统误差。

由于断面固定不变，测深误差主要来自水位观测，水文站的校核水尺应装有静水设施，起伏度小，保证了水位的观测精度。

流速仪鉴定误差由鉴定单位控制，水文站只需按规定保养仪器和及时检定。

从不利情况考虑，上述3 项误差均按《规范》给出的误差上限值确定，即断面测宽随机不确定度X'b= 2%，系统不确定度X"b= 0.5%；断面测深随机不确定度X'd= 2%，系统不确定度X"d= 0.5%；流速仪检定随机不确定度X'c= 1%，系统不确定度X"c=0.5%。

3.5 流量测验误差

单次流量测验误差由各单项误差之和得到，分别是总随机不确定度、总系统不确定度和已定系统误差。

《规范》给出一类精度水文站流速仪法单次流量测验允许误差：总随机不确定度高水±5%，中水±6%；系统误差高、中水均为-2%～-1%。

4 流量测验方案优选

多线多点长历时的施测方案误差小，精度高，但是在实际流量测验工作中，如果施测时间过长，往往水位会发生变化，也会受到其他不稳定因素影响，反而降低了测验精度。因此，需要优选误差小、精度高、施测时间短、减少工作量、最经济适用的流量施测方案。优化设计流量测验方案，按下列数学模型建立目标函数和约束条件。

以单次流量误差最小为目标函数，其表达式为：

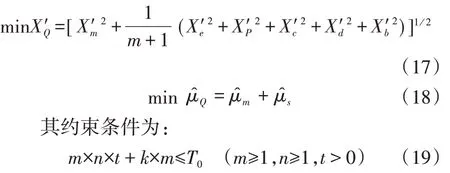
式中：m为断面测速垂线数；n为全部测速垂线上总测点数；t为单点上的测速历时（s）；k为每条垂线所需辅助历时（s）；T0为单次测流限制历时（s）。

5 结语

流量测验的随机误差、系统误差和伪误差或多或少是真实存在的，根据多垂线多测点不同测速历时的试验资料，能够组合出多种流量测验方案，从中选出精度更高且经济适用的方案。本文依托实际，严格执行《规范》，在保证流量测验精度要求、满足一次测流历时最短的前提下，确定断面测速数目、测点数目和测点测速历时等之间最佳的流量测验方案。