一道图形旋转问题的解题突破与探究
——以2021年宿迁市中考旋转压轴题为例
⦿苏州高新区实验初级中学 陈 超
1 考题初探
考题(2021年江苏宿迁中考数学试卷第27题)已知正方形ABCD与正方形AEFG,正方形AEFG绕点A旋转一周.
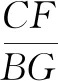
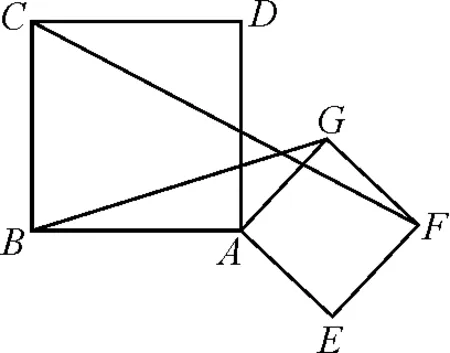
图1
(2)当正方形AEFG旋转至图2位置时,连接CF和BE,分别取CF和BE的中点为M和N,连接MN,试探究MN与BE的关系,并说明理由;
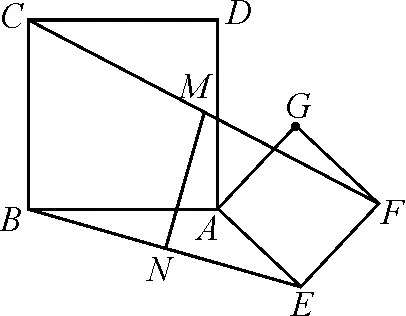
图2
(3)连接BE和BF,分别取BE和BF的中点为N和Q,连接QN,AE=6,请直接写出线段QN扫过的面积.
思路突破:本题以正方形旋转为背景开展几何探究,属于动态几何问题,解析突破需要把握运动规律,采用“化动为静”的策略,构建几何模型,利用性质定理求解.下面逐问探究.
1.1 第(1)问的探究
第(1)问求正方形AEFG绕点A旋转时其中的线段比例关系,问题中隐含了“手拉手”正方形模型,提取其中的相似关系即可求解线段比值.
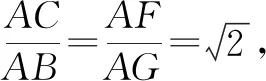
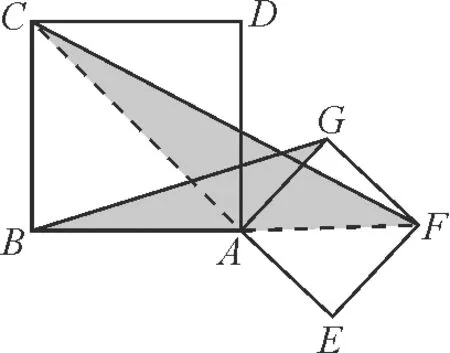
图3
1.2 第(2)问的探究
第(2)问取中点构建了线段,可以考虑采用旋转变换的方法,提取其中的全等关系,实现线段的转化,再结合其中的几何性质探究关系.
如图4,连接BM并延长使BM=MH,再连接FH,EH.可将△FMH视为是△CMB绕点M旋转180°所得,必然有全等关系,证明过程如下.因为M是CF的中点,所以CM=MF.又知∠CMB=∠FMH,则△CMB≌△FMH.由全等性质可得BC=HF,∠BCM=∠HFM.

图4
在四边形BEFC中,有∠BCM+∠CBE+∠BEF+∠EFC=360°,又知∠CBA=∠AEF=90°,所以∠BCM+∠ABE+∠AEB+∠EFC=360°-90°-90°=180°,∠HFE+∠ABE+∠AEB=180°,所以∠HFE=∠BAE.又知四边形ABCD和四边形AEFG为正方形,所以BC=AB=FH,EA=EF,则△BAE≌△HFE,从而BE=HE,∠BEA=∠HEF.因为∠HEF+∠HEA=∠AEF=90°,所以∠BEA+∠HEA=90°=∠BEH,可证△BEH为等腰直角三角形.
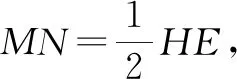
1.3 第(3)问的探究
第(3)问中同样取线段BE和BF的中点,求线段QN扫过的面积,显然需要确定线段QN的运动轨迹.由于点Q和N两点因旋转而发生位置变化,可知点Q和N的轨迹为圆,因此,只需确定轨迹圆的圆心和半径即可.
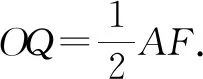
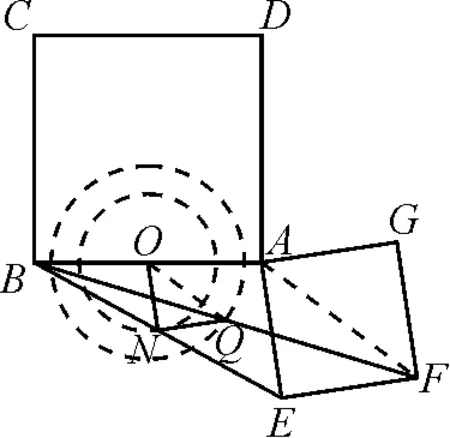
图5
2 深度探究
上述一道中考几何旋转题中涉及到了众多的知识点和几何模型,如图形旋转、三角形相似、中位线性质、圆环面积,以及“手拉手”模型等.其中第(3)问为考题的核心之问,考查学生对几何运动规律的把握,从本质上来看,可将其归为线段旋转扫过的图形面积问题,下面对此进一步深入探究.
2.1 线段旋转归纳
对于线段旋转扫过的图形面积问题,需要关注两点:一是旋转中心和旋转线段长度;二是二者的相对位置关系.尤其是后者,将直接决定旋转图形的形状,以及适用的公式.以旋转中心O和旋转线段AB的相对关系为例,下面分三种情形加以探究.
(1)旋转中心在旋转线段上
旋转中心在旋转线段上,即旋转线段绕着自身上的一点旋转,则其旋转图形会出现两种情形.如图6-1,设AO=a,BO=b,a>b,旋转角度为α.
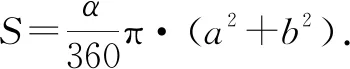

图6-1

图6-2
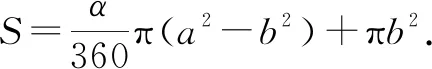
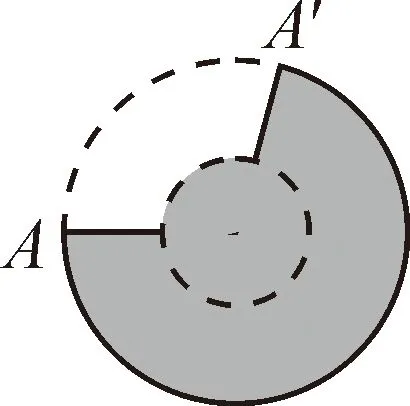
图6-3
(2)旋转中心在旋转线段的延长线上
当然图形的旋转中心也可在旋转线段的延长线上,如图7-1所示.可设AO=a,BO=b,a>b,旋转角度为α.
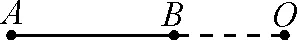
图7-1
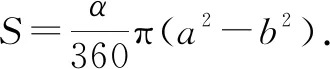
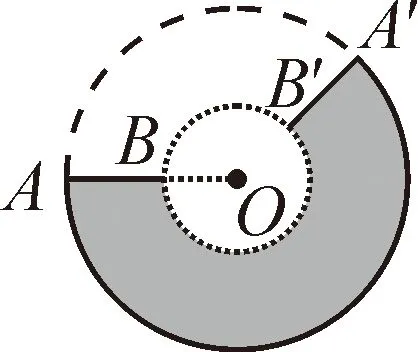
图7-2
(3)旋转中心不在旋转线段及其延长线上
原考题就属于该种情形,当线段AB的两个端点分别是线段AB上到旋转中心O的距离最长和最短点时,如图8-1所示.可设AO=a,BO=b(a>b),旋转角度为α.
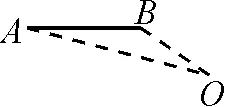
图8-1
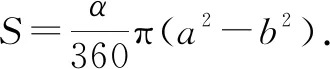
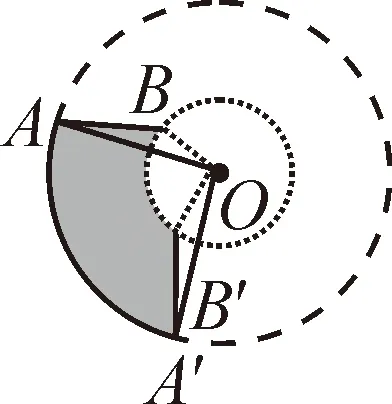
图8-2
2.2 考题关联探究
线段旋转问题在初中数学中十分常见,其中的规律具有极强的应用性,同时不同情形之间含有一定的联系,本质上同为环形及圆形的面积割补.实际考查时常采用几何探究的方式,下面结合实例进一步探究.
问题(1)操作:如图9-1,在线段AB所在直线上取一点O(点O在线段外),线段AB绕着点O旋转一周,可得如图9-2所示的圆环,则环形面积就为线段AB扫过的面积.记AB=2,OA=1,则线段AB扫过的面积为.
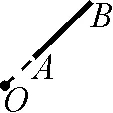
图9-1
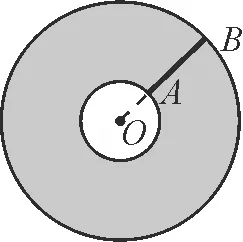
图9-2
(2)如图10所示,在Rt△ABC中,已知∠C=90°,∠B=30°,AC=2.将△ABC绕着点A旋转一周,试判断线段BC扫过的图形,并求出图形的面积.
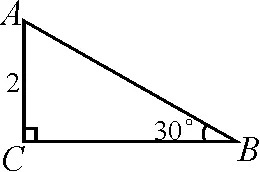
图10
(3)若将图10中的Rt△ABC绕着点C旋转一周,试判断线段AB扫过的图形,并求出图形的面积.
分析:上述是关于几何线段旋转的问题,题目中所探究的3问实则就是线段相对于旋转中心的三种情形,只需根据总结的规律来构建面积模型即可.
解:(1)该情形为旋转中心O在旋转线段AB的延长线上,则线段AB扫过的面积为环形.由AB=2,OA=1,可得OB=3.所以环形的面积S=π(OB2-OA2)=8π.
(2)△ABC绕着点A旋转一周,该情形为旋转中心A不在旋转线段BC及其延长线上,则旋转图形为圆环.在Rt△ABC中,可求得AB=2AC=4.故圆环的面积S=π(AB2-AC2)=12π.
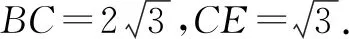
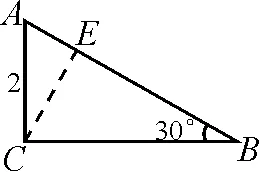
图11
评析:上述为几何线段旋转探究题,其中涉及到了线段旋转的两种情形,问题解析分两步进行.①判断旋转中心与旋转线段的相对位置关系;②引入环形面积模型,确定圆的半径,利用面积公式求解.
3 教学思考
上述以一道几何旋转考题为例进行了探究,并立足核心之问开展深度探究,围绕线段旋转的三种情形构建模型,并总结规律,对于理解线段旋转,强化旋转知识有着一定的帮助.下面基于教学实践进行深入反思.
3.1 关注几何旋转,挖掘旋转本质
上述考题以正方形旋转为背景开展几何探究,旋转是图形运动的重要形式,掌握图形旋转的三要素及其特性十分重要.以上述考题为例,正方形AEFG绕点A旋转一周,其中旋转中心为A,旋转方向逆时针或顺时针均可行,旋转角度为360°,正方形旋转到任何位置,其特性均不变.实际教学中要引导学生理解旋转的定义,并掌握图形旋转的过程中从图形全等的角度来理解旋转,通过全等关系来把握旋转特性.
3.2 把握模型特征,归纳模型特性
几何压轴题中往往综合了众多的几何模型,利用模型将知识考点融合在一起.因此,解题探究要关注问题中的模型,提取模型特征,充分利用模型性质来转化问题条件.如上述考题实则以“手拉手”正方形相似模型为背景创设命题,该模型具有“相似”特性,包括正方形相似和三角形相似.以上述考题为例,题干中正方形ABCD与正方形AEFG显然为相似关系,旋转过程中衍生了△CAF∽△BAG.教学中要引导学生提取模型,归纳模型的核心特性,并结合几何知识加以证明,强化学生对模型的理解.
3.3 探索问题内涵,总结生成规律
考题的第(3)问本质上是求旋转线段扫过的图形面积,并且旋转中心不在旋转线段及其延长线上,这是问题的本质特征.上述基于旋转线段进行了深度探究,并立足三种情形总结图形规律及面积公式,形成类型问题的解题策略,其探索过程具有一定的参考价值.教学中要引导学生探索问题内涵,挖掘问题本质,基于问题特征开展深度探究,总结规律,帮助学生积累解题经验,提升数学思维.

