浅析基于传递闭包法对供水管网压力监测点的布置

杨启航，周 艳，王晨婉

（天津理工大学环境科学与安全工程学院,天津 300384）

水是生命之源,是人类不可缺少的资源之一,全球淡水资源的储存量匮乏,人均占有量极少。据统计我国每年由于泄漏而引起的水损失高达数亿元。

以往研究中,压力监测点的布置分为两种：包括经验法和理论法。经验法是根据以往的大量的工作经验,通过观察等直接布置压力监测点,这种方法往往不具备普遍适用性,尤其是在不同的地形和城市规划不能保证布置的科学有效[1]。理论法是通过一系列的数学模型,依靠数学方法和理论,确定压力监测点的位置。在国内通常使用的方法包括：灵敏度分析、遗传算法、FCM聚类、蚁群算法等[2-5]；另外,其他的压力监测点的选取方法往往都是通过考虑单维的压力变化,或者对多个变量同时进行考虑,作为监测点布置的约束条件。舒诗湖以模型校核精度最大化以及监测成本最小化作为双目标来布置压力监测点[6]；刘书明等将管网监测范围中水压相关节点个数、水量覆盖作为目标函数,在实际管网中确定测压点优化选址[7]。这些方法简单有效,能够合理地选取压力监测点。压力监测点的首要目的是能够通过管网压力异常的变化进行漏失识别,每个压力监测点能够监测足够多的压力变化数据,这样才能有效保证当出现漏损时,所布置的压力监测点能够及时有效地监测到泄漏情况。

本文通过Python调用EPANET对管网进行水力模拟,得出管网节点压力变化,建立模糊矩阵,基于传递闭包进行聚类的方法,以可靠性和经济性为主要目标,对压力监测点进行选择。该方法简单可行,监测点布置的经济合理。

1 传递闭包算法

1.1 模糊相似矩阵

设供水管网有n个节点,在ΔQk节点处产生了一个的节点流量变化值,整个管网的节点水压都会受到不同程度的影响,被考察节点i的水压变化值为ΔHi,用ΔHi/ΔQk表示k节点处节点流量变化在节点i处产生的水压变化率,它反映了节点i水压受其他节点流量变化影响的大小。但是水压和水量的变化相差较大,并且数量级不同,因此通过因流量的变化引起节点的压力改变量,计算压力的变化率,来确定不同节点的相关程度。因节点i流量变化而引起的节点j的压力变化值为ΔHi,影响系数记作X（i, j）。

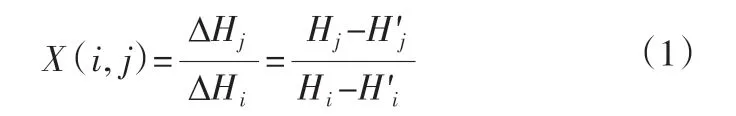
式中：Hi和Hj是节点i和节点j的原始压力；H'i和H'j是节点i和节点j变化后的压力。

供水管网所有节点的影响系数X（i, j）可用矩阵[X]n×n表示,称之为水量影响矩阵。

1.2 传递闭包法

从数学上来说,传递闭包是在集合X上求包含关系R的最小传递关系。从关系图的角度来说,如果原关系图上有i到j的路径,则其传递闭包的关系图上就应有从i到j的边。通俗地讲,就是确定每个点是否能到达其他每个点。传递闭包法聚类首先需要通过标定的模糊相似矩阵R,然后求出包含矩阵R的最小模糊传递矩阵,即R的传递闭包,最后依据进行聚类。

1.2.1 节点相似程度

选择模糊相似系数标定方法中的绝对值减数方法,取c=0.1,m=n,得到模糊相似矩阵,记作。

式中：rij为相似程度,为节点i和节点j的相似性。

1.2.2 检验模糊等价矩阵的三条性质

定义：设R=（rij）n×n为论域U上的模糊矩阵（模糊关系）性质包括：①若对任意的i,都有rij=1,则称R满足自反性；②若对任意的i和j,都有rij=rji,则称R满足对称性；③若有RoR包含于R,则称R满足传递性。

2 实例分析

基于某管网的水力模型分析,该模型由12根管段和8个节点组成,各节点的基础需水量、压力、流量等均可通过EPANET软件获得。运用EPANET建立实例管网的计算机微观模型,以节点22为例,在节点22的基础上增加用水量的20%,得到新的水力平衡。当节点22的用水量增大时,其余各个节点的流量也会产生一些影响,从而导致其余各个节点压力变化,其他节点同理。由于管网管径管长等一些因素,任意节点的流量增加都会对其他节点产生不同的影响,两种变化量不同,因此,需要分别计算管网所有节点流量变化对其他节点的影响。设定各个节点的基础用水量增加20%,基于EPANET软件模拟供水管网的变化情况,对节点压力相关性的定量分析。

2.1 基于机理公式建立水量影响矩阵

基于EPANET软件根据各个节点的基础用水量变化20%,得到新的水力平衡。由式（3）～式（5）可以建立节点水压变化之间的关系,确定水压变化敏感的节点。该供水管网有8个节点,其各个节点的水压变化见表1。

表1 各节点水压变化情况

对以上各个水压变化率由式（3）进行处理：

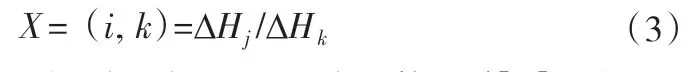
经过计算机处理得到一个8×8影响系数矩阵［X］8×8如下：

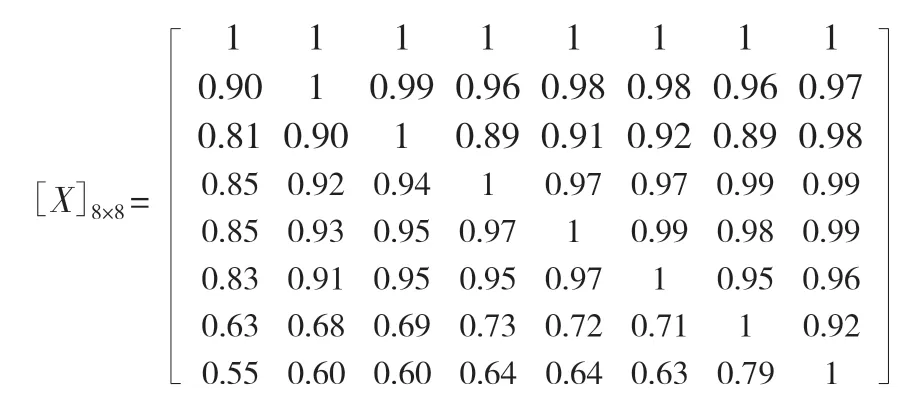
对矩阵［X］8×8中的元素使用标准偏差进行标准化,可得出新的系数影响矩阵［X'］8×8,得出水量影响系数矩阵里的各列的平均值均为0,方差均为1。结果表明：经过标准的标准差处理,在元素改变的情况下,也可以保证数据的稳定性。对系数影响矩阵［X'］8×8的各列元素标准化处理,见式（4）。由此,得出水量系数影响的最终矩阵［X''］8×8如下：

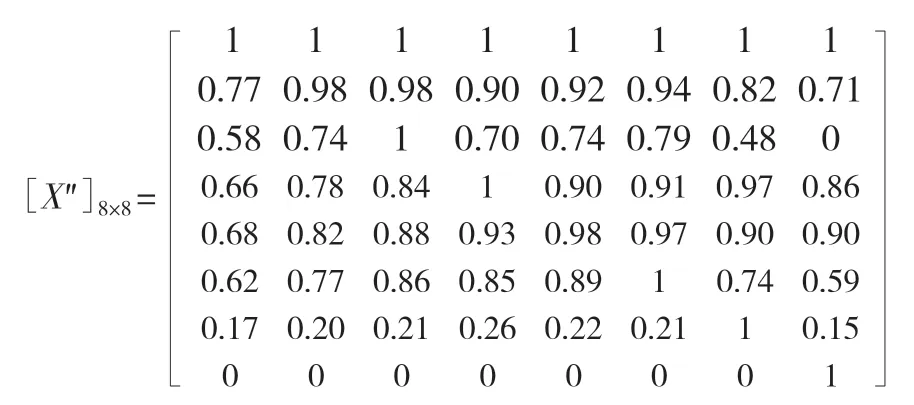
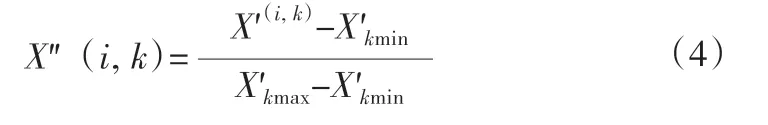
2.2 基于传递闭包进行聚类

选择模糊相似系数标定方法中的绝对值减数方法,取c=0.1, m=n,得到模糊相似矩阵。rij称为相似程度,见式（5）。

结合模糊相似系数标定方法中的绝对值减数法及水量系数影响的最终矩阵［X''］8×8得道矩阵R8×8。经检验,该矩阵满足模糊等价矩阵中的两条性质,自反性与对称性,但是不满足传递性,即ROR不包含与R。因此,需要将模糊矩阵自乘R·R=R2,得到R2,然后再自乘R2·R2=R4,…,直到R2k=Rk时为止,此时t（R）=Rk即为所求。本文通过MATLAB编程计算得到t（R）矩阵。

基于t（R）矩阵进行聚类分析。此次聚类是一种动态聚类,动态聚类的过程就是求模糊等价矩阵R*的∈[0,1]水平截集R 的过程,水平截集是一个布尔矩阵,也是一个等价矩阵。当 从1 逐渐变为0时,R 不断变化,这个过程形成了一个动态聚类关系,从而得到不同节点的分类。

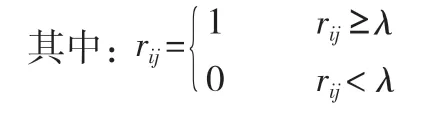
因此,取值不同,最终的结果不同,当 取0.96 时,整个管网分为7 类：{1},{2},{3},{4,5},{6},{7},{8}；当取0.93 时,整个管网分为6 类：{1},{3},{2,4,5},{6},{7},{8}；当取0.92 时,整个管网分为5 类：{1}{2,4,5,6},{3},{7},{8}。

经过考虑供水管网的可靠性和经济性,确定 =0.92 时,压力监测点布置最合理有效,最终分为5 类：节点11；节点12、21、22、23；节点13；节点31；节点32。

3 结论

本文首先介绍当前国家的水资源存储情况,综合压力在供水管网中的主要地位,选择压力监测点为本文主要的研究内容,并论述国内外学者对管网压力监测点布置的方法,提出以模糊聚类中传递闭包为压力监测点选取的主要手段。通过Python调用EPANET软件实现对管网的数值模拟,确定各个节点之间相关程度,以节点之间相关性和节点灵敏度为主要指标,运用传递闭包选出最佳监测点位置。该方法经济有效,能够对管网实时监控,保证了管网的正常运行。