基于多代竞争遗传的车辆配送路径多峰寻优研究
王力锋 黄斐 黄谦 任宇光 陈文冬


摘 要:为了高效完成车辆配送路径多峰寻优任务,提出基于多代竞争遗传的车辆配送路径多峰寻优方法。设计车辆配送路径多峰寻优的目标函数与约束条件,构建开放式车辆路径优化模型,求解车辆路径优化的路径多峰寻优目标函数,引用多代竞争遗传方法,求解车辆配送路径多峰寻优模型,完成车辆配送路径多峰寻优。仿真实验结果显示:所提方法对模拟区域车辆配送路径实施多峰寻优时,4辆车的配送时间均值为47.43h、迭代次数均值为149次、寻优时间均值为2.40s,寻优时间较短,车辆配送成本较少,实际应用价值显著。
关键词:物流;多代竞争遗传;车辆配送;路径寻优;多峰寻优
中图分类号:U116 文献标识码:A
Abstract: In order to efficiently complete the multi peak optimization task of vehicle distribution path, a multi-modal optimization method of vehicle distribution path based on multi-generation competitive genetic algorithm is proposed. This paper designs the objective function and constraint conditions of multi peak optimization of vehicle distribution path, constructs an open vehicle routing optimization model, solves the multi peak optimization objective function of vehicle routing optimization, and uses the multi generation competitive genetic method to solve the multi peak optimization model of vehicle distribution path, and completes the multi peak optimization of vehicle distribution path. The simulation results show that the average distribution time of four vehicles is 47.43h, the average number of iterations is 149, and the average optimization time is 2.40s. The optimization time is shorter, the vehicle distribution cost is less, and the practical application value is significant.
Key words: logistics; multi generation competitive inheritance; vehicle distribution; path optimization; multimodal optimization
0 引 言
合适的车辆配送路径,将缩短运输距离,减少配送成本,配送时间也将得以缩短,目前很多研究人员对车辆配送路径寻优问题进行了深入研究,例如叶勇等[1]提出基于狼群算法的车辆配送路径寻优方法,该方法可在降低车辆配送成本的条件下,有效获取车辆配送最佳路径,但是该方法在获取车辆配送最佳路径时,寻优次数较多,收敛速度慢;李卓等[2]提出基于混合蚁群算法的车辆路径规划方法,蚁群算法在求解车辆路径寻优中较为常用,可在短时间内获取车辆配送最佳路径,但是在所寻路径中配送时,与同类算法相比,车辆配送成本较多,在车辆路径寻优时的收敛效率也并不显著。夏扬坤等[3]为了降低连锁超市的配送系统总成本,设计了一个自适应禁忌搜索算法,采用“随机禁忌长度”和“禁忌表重新初始化”来对邻域进行充分搜索,结合各超市配送的时效性,建立了相应的双目标数学模型,增强算法的全局寻优能力,但是其约束条件不明确,无法获取全局最优解。贺桂和等[4]为了促进农产品流通,降低农产品电商物流配送成本,将传统约束中客户需求不可拆分的条件进行松弛,结合传统带时间窗的车辆路径问题,研究了一种带软时间窗的需求单元拆分车辆路径问题,提升禁忌搜索算法的全局寻优性能,有助于减少使用的车辆数和降低配送成本,但是其算法应用过程的迭代稳定性较差,无法实现多峰寻优。戚远航等[5]提出一种泰森多边形的离散蝙蝠算法,融入了一种基于多车场多车辆问题的编解码策略,求解多车场车辆路径问题,表现出较强的寻优能力和稳定性,但是其目标函数与约束条件不明确,其不支持多峰寻优任务。
车辆配送路径多峰寻优,可理解为车辆配送路径中多个高峰期的最优路径规划,此问题属于非线性函数多峰寻优问题,本文针对此问题进行深入研究。为此,本文提出基于多代竞争遗传的车辆配送路径多峰寻优方法,本文中的多峰寻优是指在车辆配送的高峰时段下,由固定的物流中心安排可以匹配最佳路线的车辆进行配送,是面向全时间段的车辆配送路径多峰寻优,其关键在于优化遗传算法收敛效率,并在车辆配送路径多峰寻优问题中,应用多峰函数,结合闭区间上连续函数的零点存在定理,求解最优的车辆配送路径即將全局最优解转换为车辆配送路径种群规模最优化问题,以多峰寻优的目标函数与约束条件为基础,求解车辆配送路径多峰寻优模型,使其具有较为显著的优化效果。
1 基于多代競争遗传的车辆配送路径多峰寻优方法
车辆配送路径优化属于路径优化的范畴,但车辆配送路径优化与路径优化又有很大不同,主要体现在以下三个方面:(1)车辆配送路径优化对货物的重量、大小、体积、属性等有一定的规定,路径优化仅仅涉及路径规划内容,其影响因子存在差异。(2)服务时效要求不同,车辆配送时间要求更严格,一般都是在白天,因为工作人员的工作时间固定,但具体时间要求比较宽松,例如上午、下午等,工作人员的服务时间较为灵活,而路径优化的寻优过程是基于全时间段的。(3)配送后,需要进行后续的、简单的分拣作业等过程,导致其影响配送时长的因素较多,很难快速、精确地找到全局最优解。
1.1 开放式车辆路径优化
开放式车辆是指对车载货物重量、配送车辆数量等内容不设限制,不做约束。车辆配送路径多峰寻优属于动态事件,此事件具有四种情况[4-6]:(1)车辆配送时,加入新“目标”;(2)车辆配送时,初始“目标”需求发生变化;(3)车辆配送时,交通情况变差;(4)车辆配送时,配送车辆出现事故。
如果出现上述四种任何一种动态事件,便需要因地制宜的设计新的车辆配送路径多峰寻优方案。为此,构建一种基于开放式车辆路径优化的路径多峰寻优模型。
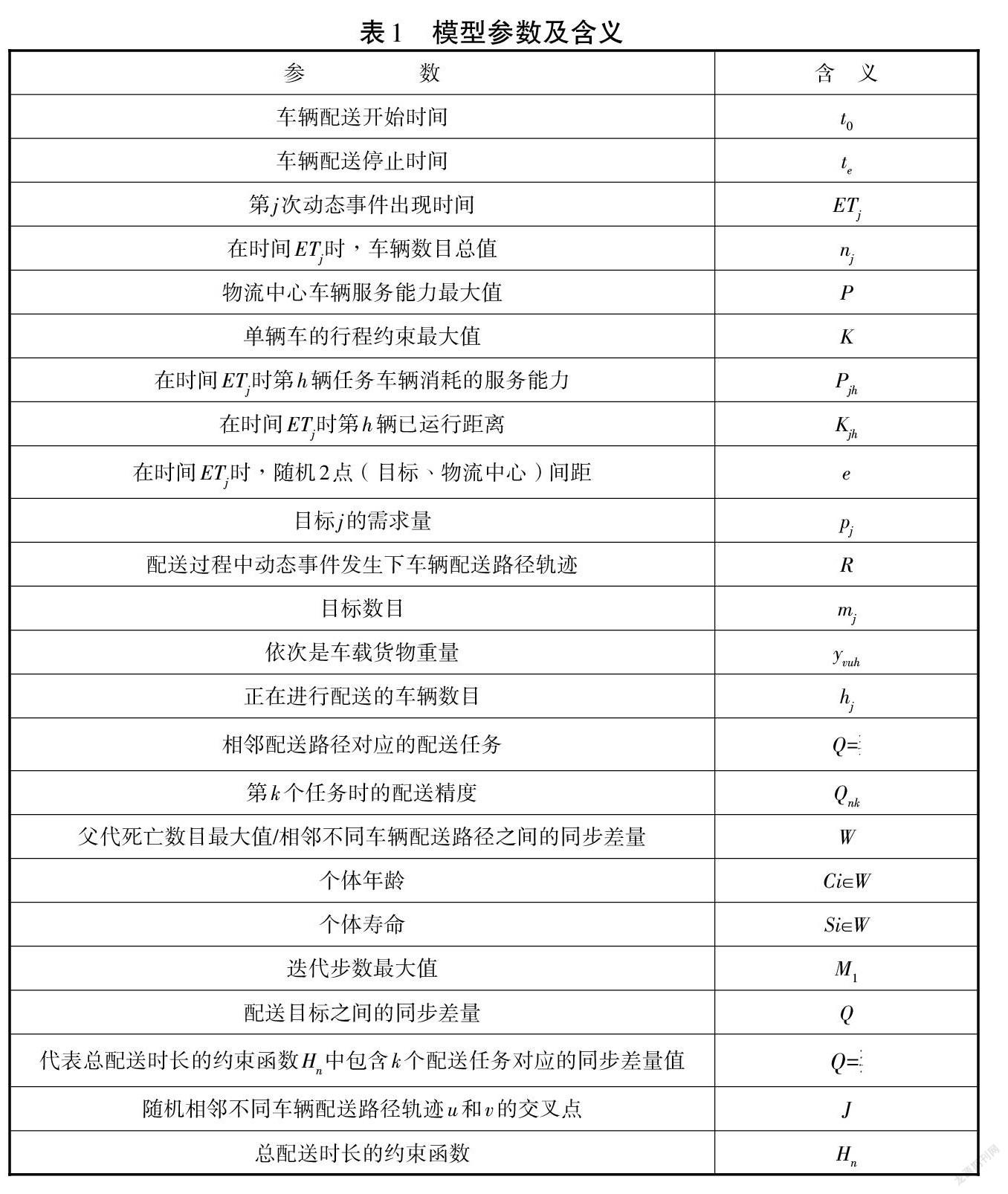
首先,设定路径多峰寻优模型所用参数,如表1所示。
其次,根据标记设立此模型中车辆配送路径多峰寻优的目标函数:
Miney (1)
车辆配送路径多峰寻优过程中的阻抗是具有实时或历史流量的时间属性,最佳路线是对指定日期和时间来说最快的路线,因此,高峰时段下车辆配送路径多峰寻优过程的目标函数与全局最优解相对应,需要应用多代竞争遗传算法中的多峰函数对其求解。
1.2 车辆配送路径的多代竞争遗传算法
为了合理安排车辆路径,使总运输路径最短,本文引入多代竞争遗传方法,进行路径多峰寻优模型设计。本文设计需在下列条件下进行:(1)假设用户分布在配送区域内,用户需求小于车辆额定载重量,每个用户只允许访问一次,只允许使用一辆车,且每辆车只允许使用一次;(2)分配到配送中心的每辆车在配送中心启动和结束时,每个用户的需求之和不超过车辆的额定。
一般来说,当遗传算法是“遗传”时,新个体将取代某些父个体在种群中的地
位[7]。然而,遗传算法(复制、交叉、突变)并不能保证后代优于父代,产生“退化”现象[8]。为了保障优秀的个体存在充足的繁殖次数,本文将“寿命优化”应用在遗传算法之中,防止出现“退化”情况,以此提高收敛效率[9-10]。
寿命即为个体在种群里的存活代数,年龄是个体目前已经存活的代数。年龄与寿命相同的个体,便属于“死亡”模式。种群之中,个体的年龄并非一致,所以便会衍生多代并存的种群结构。适应度显著的个体,寿命显著,可以繁衍多代,以此提升了优秀基因遗传至子代的几率,优化种群个体质量。种群里个体竞争分为子代个体的生存机会竞争、寿命竞争、遗传机会竞争。车辆配送路径多峰寻优时,多代竞争遗传的步骤如下:(1)多代竞争遗传中车辆配送路径初始种群建立时,假定车辆配送路径种群规模是W,车辆配送路径的初始种群适应度较差的W个个体(车辆配送路径)寿命是1,剩下优秀个体(可用路径)根据适应度实施从大到小的顺序配列,年龄都是0。繁衍一代后,全部父代个体的年龄需要加1。以此寿命是1的个体在子代个体出现后便会进入“死亡”模式,被新衍生的子代个体所取代。个体进入“死亡”模式表示某配送路径不是车辆配送路径多峰寻优目标,可舍弃[11-12]。(2)遗传操作衍生子代时,各个父体个体(车辆配送路径)进行遗传操作的几率按照自身适应度设置。为了避免车辆配送路径种群规模出现“萎缩”,各次衍生的车辆配送路径个体数目必须充足。因为父代死亡数目最大值是W,因此遗传之时,衍生的子代个体数目必须是W。去除父代死亡个体时,假定目前个体的年龄是Ci∈W,寿命是Si∈W,车辆配送路径种群通过交叉、变异衍生新一代个体时,车辆配送路径种群个体的年龄将加1。(3)子代以优胜劣汰的规则,择优录取并纳入车辆配送路径种群。假定父代个体死亡数目是Z,那么子代个体根据适应度实施对比,并择优录取,合适的车辆配送路径将被纳入车辆配送路径备选种群。(4)设置车辆配送路径种群个体寿命与年龄时,按照优胜劣汰的宗旨,子代个体(车辆配送路径)里适应度显著的个体,将纳入车辆配送路径种群。此类个体和还没有死亡的父代个体根据适应度的大小值排列,子代个体的寿命根据自身排序方位设置,年龄设成0。父代延续个体的寿命根据适应度设置。(5)车辆配送路径种群更新时,去除“死亡”个体,更新后的车辆配送路径种群,由前代延续个体与新生个体构成,车辆配送路径种群规模不变。
多次执行上述步骤,直至迭代次数为最大值,输出最优解。
此时,在车辆配送时,车载量约束是:
py<P-P (2)
车辆配送时,行驶距离约束是:
ey<K-K (3)
预设在物流中心所派遣车辆的载量约束是:
py≤P (4)
预设在物流中心派遣车辆的行驶距离约束是:
ey≤K (5)
车辆配送时,各个客户均被1辆车服务的约束是:
y=1 (6)
y=1 ; (7)
车辆配送时,全部车辆起点、终点均为物流中心的约束是:
y=y=n (8)
车辆配送时,各辆车运行的路径轨迹为圆形的约束是:
y≤R-1 (9)
车辆配送时,路径多峰寻优的效率约束是:
y=
(10)
车辆配送时,动态事件出现的时间点符合配送周期的约束是:
t≤ET<ET≤t (11)
整合上述公式,即完成的路径多峰寻优模型设计。
车辆配送路径的多代竞争遗传时,为了保障收敛效率得以优化,对遗传算法进行优化,优化之处见下述。
1.3 车辆配送路径多峰寻优
车辆配送路径多峰寻优时,使用符号对每个车辆进行编码,将编码的个体组成为车辆配送路径种群,多代竞争并存的车辆配送路径种群结构,将使用遗传与变异模式获取新的个体,取代“死亡个体”,将其转换为车辆配送路径问题,若出现新的车辆加入,在车辆配送路径种群序列里加入新车辆。根据父代种群里个体的适应度与遗传的双亲进行交叉复制,染色体的交叉复制属于双亲遗传。双亲遗传时,以拓展路径寻优范围为目的,使用多样性的邻域结构:
(1)两个体间的单个节点交换。任意选择两个体(车辆配送路径)相交的节点,设成交换点并实施转换,获取新解[13-14]。
(2)OX顺序较差。在一个父代个体里选取一辆车与其他车辆的所有相交節点,在此节点中加入其他父代个体里车辆位置,反复求解,直至解出现规模是N的车辆配送路径种群,即车辆编码顺序与车辆走过路径顺序。
为了克服遗传算法的早熟情况,求解车辆配送路径多峰寻优的目标函数时[15],需要优化可选车辆配送路径的种群个体多样性。遗传算法的搜索过程仅基于适应度函数。适应度分配方法是根据个体目标值对种群进行排序,个体适应度只取决于其在种群序列中的位置顺序。通过交叉概率与变异概率设置交叉与变异出现的概率,若迭代步数最大值是M,为了避免单个子种群,特别是个体序列的第一部分过度繁殖,导致分布过程中分布目标过多,有必要优化多峰函数,选择性地抑制子种群中的某些个体,令相邻不同配送目标之间的同步差量为Q。
假设Q=
Q,
Q,
Q,…,
Q,代表总配送时长的约束函数H中包含k个配送任务对应的同步差量值。因此,相邻不同车辆配送路径之间的同步差量W表示为:
Q=
=
(12)
式中:总配送时长的约束函数H处于第k个任务时的配送精度Q受到该段路程l的配送任务总数影响,相邻配送路径对应的配送任务可表示为Q=
q,
q,
q,…,
q,l取值1≤l≤x,当配送作业过程的配送目标过多时,配送精度逐渐减少,但相邻不同车辆配送路径之间的同步差量对应减少,车辆与车辆之间的多峰函数此消彼长,体现了划分种群、调整个体适应度以提高种群多样性的原则,即具有多峰优化性能,且不增加算法复杂度,便可停止车辆配送路径多峰寻优,输出车辆配送路径多峰寻优结果,完成车辆配送路径多峰寻优。
2 仿真分析
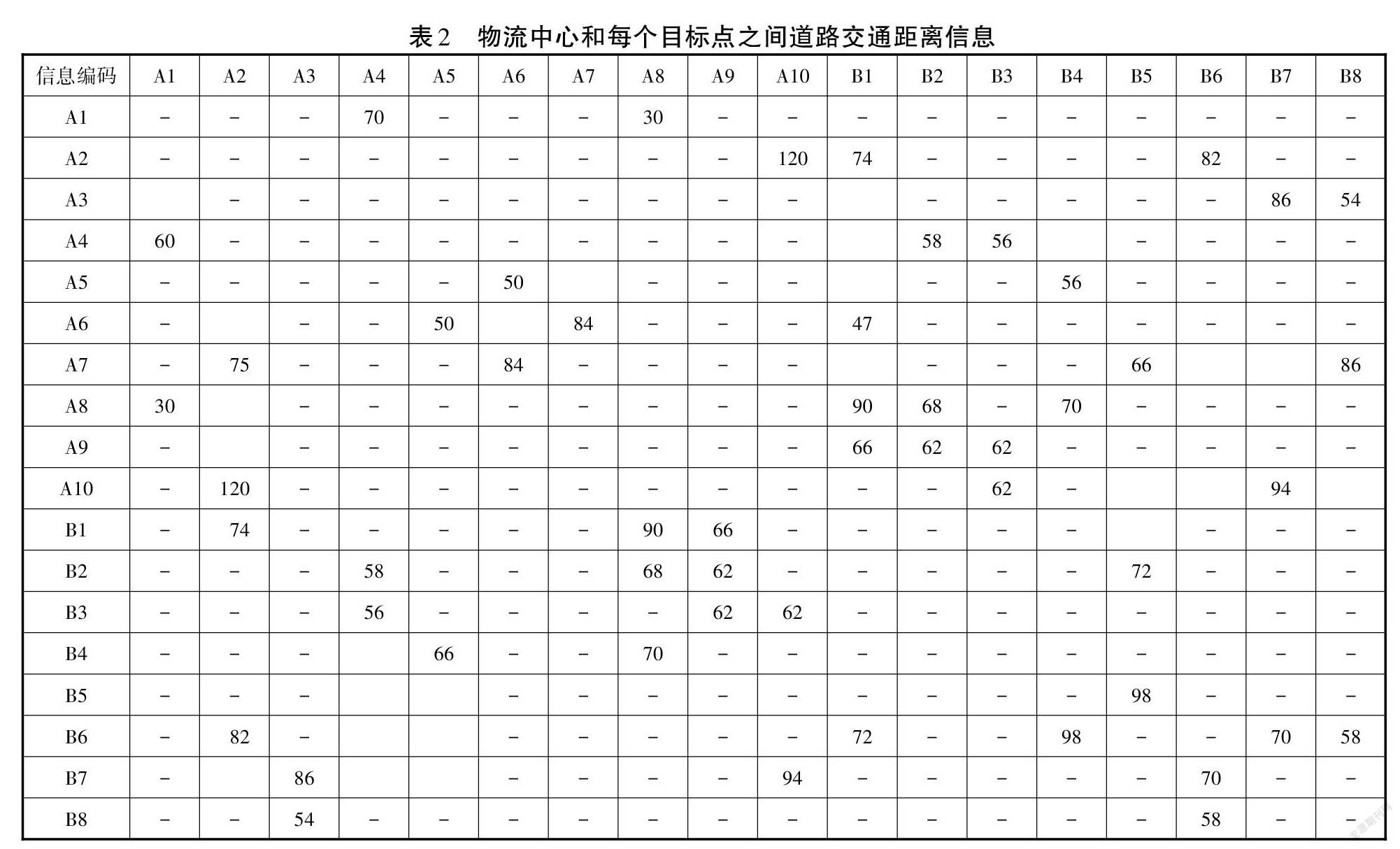
为测试本文方法对车辆配送路径多峰寻优问题的使用性能,在CodeBlocks编程环境中,通过C语言编程,基于Inter(R)Core(TM)i3 CPU、内存是4.0GB、64位Windows10旗舰版操作系统的计算机之中编程本文所提方法,模拟分析本文方法对车辆配送路径多峰寻优的效果。仿真环境中,所模拟的物流中心和每个目标点之间道路交通距离信息如表2所示。
表2中,A1、A2、A3、A4、A5、A6、A7、A8、A9、A10代表配送城市;B1、B2、B3、B4、B5、B6、B7、B8表示配送城市的十字交通路口,此路口不存在目标。
使用本文方法对该区域车辆配送路径进行多峰寻优时,配送车辆的详细配送顺序是:配送车辆1配送路径规定时间:物流中心出发时间为6:30,19:50返回物流中心。配送车辆2配送路径规定时间:物流中心出发时间为7:30,16:30返回物流中心。配送车辆3配送路径规定时间:物流中心出发时间为7:30,18:40返回物流中心。配送车辆4配送路径规定时间:物流中心出发时间为5:30,19:50返回物流中心。
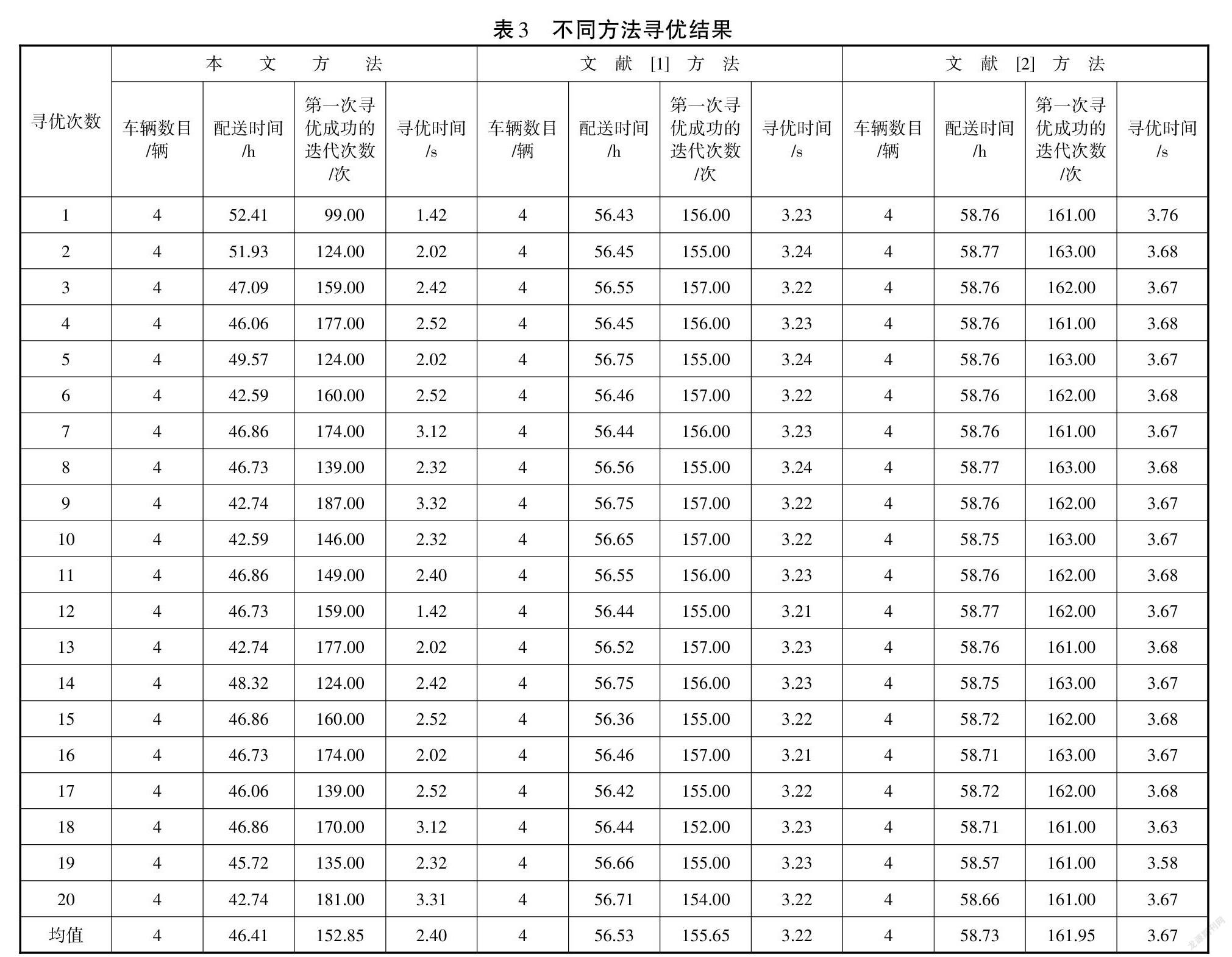
在初始种群建立后,依据种群个体多样性,迭代步数最大值是M时,进行了多峰函数寻优,在无动态事件出现的前提下,使用本文方法与其他文献方法(文献[1]和文献[2]方法)对该区域车辆配送路径进行多峰寻优后的结果,而本次实验给出的数据为第一次寻优成功的迭代次数(多峰函数的第一个取值即第一个峰),如表3所示。
如表3数据所述,本文方法在对该区域车辆配送路径实施多峰寻优时,使用4辆车、配送时间均值为46.41h、迭代次数均值为152.85次、寻优时间均值为2.40s。为凸显本文方法对车辆配送路径多峰寻优的使用效果,将其与文献[1]的基于狼群算法的车辆配送路径寻优方法、文献[2]的基于混合蚁群算法的车辆路径规划方法进行对比后,两种对比方法的车辆配送路径寻优结果的车辆配送时间、迭代次数、寻优时间均大于本文方法,表明本文方法和同类方法相比,在车辆配送路径多峰寻优时,存在效率优势。
为了增加算例分析的展现形式,体现本文方法的多峰性质,将表3转换为图1,突出对多峰配送优化求解的过程、优越性。
由图1可以看出,本文方法较文献[1]和文献[2]方法的多峰函数解即有多个极值点的函数解,也就是说其峰值较多,没有个体的区间不可能包含极值点,因此,本文取出包含个体的区间,再次细化,重复搜索过程,直到细化的区间足够小,可以更有针对性地获取最优解,进而为车辆配送路径寻优提供更为优越的求解过程。
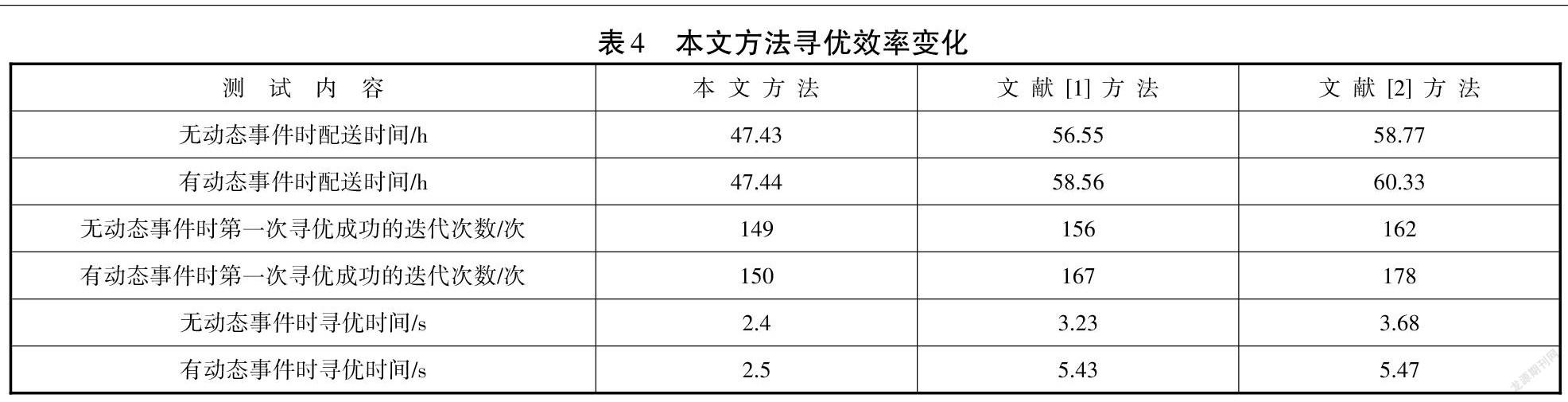
在仿真环境中,引入本文所设计四种动态事件中的事件(3),测试本文方法、文献[1]的基于狼群算法的车辆配送路径寻优方法、文献[2]的基于混合蚁群算法的车辆路径规划方法的寻优效率,并将此前提条件下的寻优效率与无动态事件出现前的效率进行对比,结果如表4所示。
如表4所示,在仿真环境中,引入本文所设计四种动态事件中的事件(3)后,本文方法寻优下,车辆配送时间比无动态事件时多出0.01h,第一次寻优成功的迭代次数多比无动态事件时多出1次,寻优时间比无动态事件时多0.1s;文献[1]方法使用后,车辆配送时间比无动态事件时多出2.01h,第一次寻优成功的迭代次数多比无动态事件时多出11次,寻优时间比无动态事件时多2.2s;文献[2]方法使用后,车辆配送时间比无动态事件时多出1.56h,第一次寻优成功的迭代次数多比无动态事件时多出16次,寻优时间比无动态事件时多1.79s。由此可见,动态事件的出现,对文献[1]方法、文献[2]方法应用效果存在影响,但对本文方法的影响不大。且文献[1]方法、文献[2]方法与本文方法相比,动态事件出现后,本文方法对车辆配送路径多峰寻优效率仍旧最为显著。
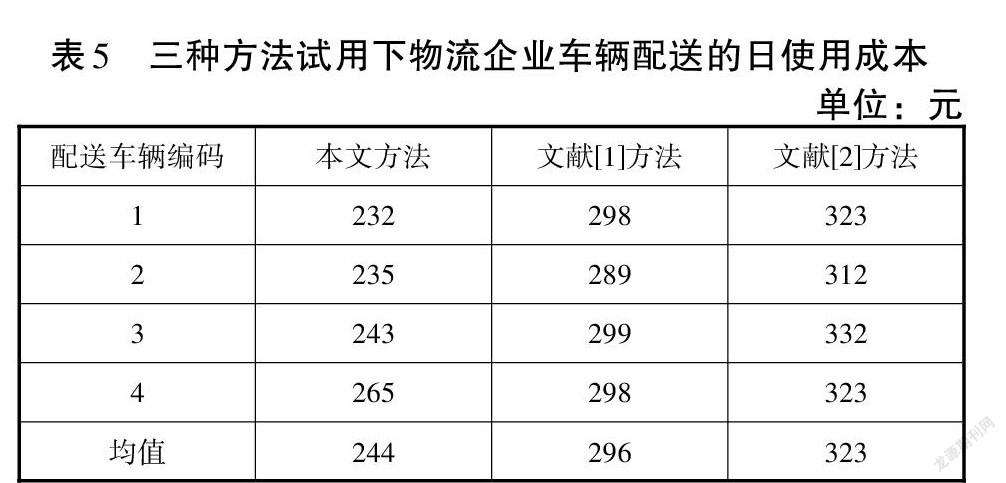
本文方法、文献[1]的基于狼群算法的车辆配送路径寻优方法、文献[2]的基于混合蚁群算法的车辆路径规划方法使用下,模擬计算物流企业车辆配送的使用成本进行对比,按功能计算物流成本计算车辆折旧或修理费用、通行费、燃料费、司机工资和其他费用,降级整合为最终成本,三种方法的最终成本对比结果如表5所示。
如表5所示,三种方法对比之下,物流企业使用本文方法后,物流企业4辆车辆配送的日使用成本均值是244元,使用文献[1]方法、文献[2]方法,物流企业4辆车辆配送的日使用成本均值分别比本文方法多出52元、79元。对比之下,本文方法寻优下,更节省车辆配送的应用成本。
3 结 论
(1)第三方物流企业中,物流中心的车辆路径规划十分重要,不仅需要准确无误地将货物配送至最终客户,也需要保证车辆的配送时效。针对车辆配送问题进行专题研究,提出了基于多代竞争遗传的车辆配送路径多峰寻优方法。
(2)所提方法有效提升了遗传算法的收敛效率,可在短时间内获取车辆配送的最佳路径,且其配送时间、迭代次数、寻优时间均得到保证,在最短时间内完成车辆配送路径寻优。且使用成本最少,在生产企业、物流企业的实际应用过程中均存在参考价值。
参考文献:
[1] 叶勇,张惠珍. 多物流中心车辆路径问题的狼群算法[J]. 计算机应用研究,2017,34(9):2590-2593.
[2] 李卓,李文霞,巨玉祥,等. 混合蚁群算法求解带软时间窗的车辆路径问题[J]. 武汉理工大学学报(交通科学与工程版),2019,43(4):761-766.
[3] 夏扬坤,符卓. 带软时间窗的连锁超市配送车辆路径问题[J]. 信息与控制,2018,47(5):91-97.
[4] 贺桂和,夏扬坤,朱强. 需求單元拆分的农产品电商配送车辆路径优化[J]. 信息与控制,2018,47(3):109-116,124.
[5] 戚远航,蔡延光,蔡颢,等. 泰森多边形的离散蝙蝠算法求解多车场车辆路径问题[J]. 控制理论与应用,2018,35(8):95-103.
[6] Nowak M, Archetti C, Kamiński, Bogumił. Preface: Special issue on the future of route optimization/vehicle routing[J]. Networks, 2019,73(4):379-381.
[7] 冯亮,梁工谦. 基于GPS/GIS协同的动态车辆调度和路径规划问题研究[J]. 计算机科学,2017,44(9):272-276,285.
[8] 陈久梅,张松毅,但斌. 求解多隔室车辆路径问题的改进粒子群优化算法[J]. 计算机集成制造系统,2019,25(11):2952-2962.
[9] Reihaneh M, Ghoniem A. A multi-start optimization-based heuristic for a food bank distribution problem[J]. Journal of the Operational Research Society, 2018,69(5):691-706.
[10] 葛显龙,谭柏川,吴宁谦. 基于碳交易机制的带时间窗车辆路径问题与算法研究[J]. 管理工程学报,2018,32(4):141-148.
[11] Salhi S, Rand G K. Improvements to Vehicle Routeing Heuristics[J]. Journal of the Operational Research Society, 2017,38(3):293-295.
[12] 吴亮然,林剑,刘毅志,等. 基于车辆配送线路的区域协同配送方法[J]. 计算机工程与应用,2020,56(1):244-250.
[13] 李军涛,路梦梦,李都林,等. 模糊时间窗多目标冷链物流路径规划[J]. 中国农业大学学报,2019,24(12):128-135.
[14] 张美. 海上应急物资配送路径规划模型的构建[J]. 舰船科学技术,2019,41(22):209-211.
[15] 马冰山,胡大伟,陈希琼,等. 半开放式的多配送中心纯电动车辆路径优化问题[J]. 交通运输系统工程与信息,2019,19(6):199-205.

