那苏瓦卡里水电站沉沙池沉沙及冲沙效果研究

高东红 邹浩

摘要： 在水利水电工程中一般都采用沉沙池来降低泥沙含量，减小泥沙对引水发电系统产生的不利影响，沉沙池中含沙水流流态及沉沙冲沙效果的研究就显得极为重要。基于尼泊尔那苏瓦卡里水电工程的沉沙池，采用理论公式、RNG  k～ε 紊流模型及体积分辨率函数VOF模拟计算了沉沙池内水沙两相流的水流形态，并详细展示了多组分泥沙颗粒组合中不同颗粒直径泥沙的沉积效果。结果表明：不小于0.2 mm粒径的泥沙沉沙率达到95%以上，数值计算结果与采用理论公式计算得出的沉沙率保持较高的吻合性，满足工程设计要求。

关 键 词： 沉沙池; 沉沙率; 数值计算; 那苏瓦卡里水电站; 尼泊尔

中图法分类号：  TV68

文献标志码：  A

DOI： 10.16232/j.cnki.1001-4179.2022.03.019

 0 引 言

自然界河流中多含有泥沙，水流中的泥沙通常会对水利水电工程带来诸多不利影响。近年来部分学者陆续对三峡水库、小浪底水库的泥沙淤积  [1-2] 、水工建筑物及水轮机组磨损  [3] 等问题开展了研究。

19世纪开始，含沙水流的理论研究就取得了飞速发展。Duboys  [4] 提出了推移质运动的拖拽力理论，Rouse  [5] 则提出了著名的悬移质泥沙浓度分布公式。中国学者窦国仁  [6] 则提出了表示纵向脉动流速沿竖直线分布的公式;蔡树棠  [7] 从流体力学基本理论出发，讨论了泥沙在湍流中对水相对速度、脉动速度的改变，泥沙在二维渠道均匀定常流动中含沙量的垂直分布和通常的扩散理论修正等3个问题。

从本质上讲，含沙水流属于固液两相流理论研究范畴，泥沙数值模拟主要基于两相流理论。随着计算机技术的发展，数值计算越来越广泛地用于含沙水流计算中。中国西部地区及在世界众多国家的河流中均含有大量泥沙，泥沙问题成为众多水利水电工程的制约因素。解决引水系统中的泥沙问题，通常是依靠修建沉沙池及其冲沙系统，而沉沙池中水沙流动分析常借助于数值计算。在沉沙池数值计算方面，杨红等  [8] 进行了沉沙池立面流场模拟计算，胡斌等  [9] 进行了沉沙池的三维流场模拟，周晓泉、张军等  [10-11] 分别对复杂边界条件下及圆中环沉沙池的三维紊流场进行了数值模拟研究。

尼泊尔地区多数为多泥沙河流，修建水电站工程通常需考虑沉沙池。岳竹等  [12] 等研究了尼泊尔内有压隧洞内沉沙池泥沙沉降特性。本文结合那苏瓦卡里水电站工程，对冲沙设施的结构设计理论及布置进行了详细论述，并运用大型流体计算软件对沉沙池中多组分泥沙颗粒的流态及沉沙效果进行数值模拟验算，选用较为成熟的湍流模型 RNG  k～ε 模型，应用流体积函数VOF追踪自由液面研究了沉沙池中泥沙沉积效果  [13] ，为工程设计和运行提供了依据。

1 工程概况

那苏瓦卡里水电站位于尼泊尔东北部地区，背靠喜马拉雅山脉，地势北高南低，河谷狭窄、岸坡陡立、阶地较为发育，且河床落差较大。此外由于山体植被覆盖较少，小型崩塌、滑坡及古滑坡体均较为发育，水土流失较严重，尤其是在雨季，山体滑坡频发，河水泥沙含量较大。

工程从Bhotekoshi河引水，通过4.194 km长的引水隧洞后进入地下发电厂房。发电水头达168.0 m，设计发电流量为80 m  3 /s，总装机容量110 MW。

整个枢纽河段河谷狭窄，受限于现场地形地质条件，河流两侧没有足够缓坡和滩地布置沉沙池，因此采用地下式沉沙池。

初拟地下沉沙池为3个独立的洞室，位于河流右岸的山体里面，其上游连接段与取水隧洞相相接。在正常情况下，3个独立的沉沙池连续运行。沉沙池主要尺寸为：上游连接段长度 32.0 m，工作段长度125.0 m，工作宽度15.0 m，下游连接段 24.5 m ;沉沙池工作水深13.0 m，底坡坡率0.02。

下游连接段布置有出口闸及闸室、排沙闸及闸室、沉沙池操作洞、排沙道等。下游连接段经断面收缩后与沉沙池出水隧洞相接，沉沙池总体平面布置如图1所示。

2 沉沙池中沉沙率理论分析

2.1 泥沙基本资料

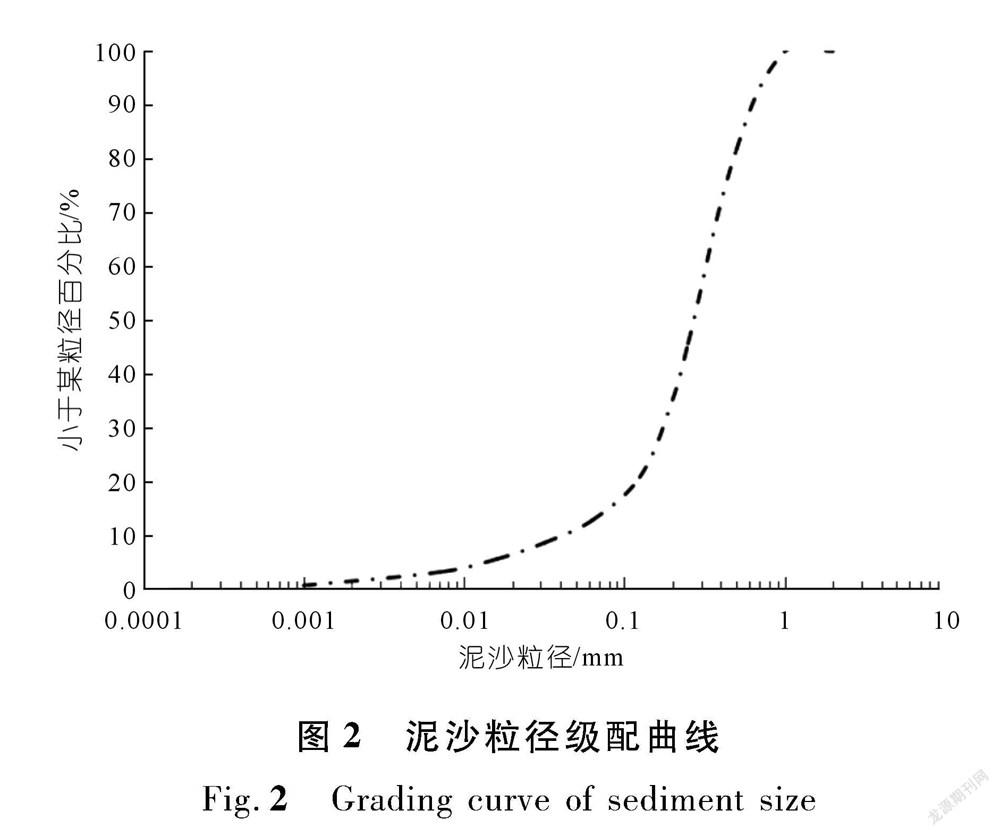
实测首部樞纽所在河段汛期泥沙浓度为5.624 kg/m  3 ，泥沙粒径级配曲线见图2。

2.2 泥沙沉降理论分析

2.2.1 沉沙池设计要求

根据工程特点及业主要求，单个沉沙池的设计应满足以下要求：

① 粒径大于等于0.2 mm的泥沙沉降率应大于95%;

② 工作段平均最大流速为0.2 m/s;

③ 沿程冲洗段的平均流速应大于2.5 m/s。

2.2.2 沉沙率理论分析

（1） 泥沙沉速计算  [14] 。

当泥沙粒径小于等于 0.062  mm时，采用斯托克斯公式：

ω= g 1800 （ ρ  s -ρ  w  ρ  w  ） d 2 γ  （1）

γ= 0.01775 1+0.0337t+0.000221t 2  （2）

当粒径为0.062～2.000 mm时，采用沙玉清天然沙沉速公式：

（ lg S a+3.790）  2+ （ lg ψ-5.777）  2=39.0 （3）

沉速判数：

S a= ω g  1/3  （ ρ  s  ρ  w  -1）   1/3 γ  1/3   （4）

粒径判数：

ψ= g  1/3  （ ρ  s  ρ  w  -1）   1/3 d 10γ  2/3   （5）

当粒径大于2.0 mm时，采用沙玉清紊流沉速计算公式：

ω=4.58 10d  （6）

上述式中： γ 为水的运动黏性系数，cm  2 /s，20 ℃时为 0.010 07  cm  2 /s; t 为水温，℃; d 为泥沙粒径，mm; ρ   s 为泥沙密度，取2.65 g/cm  3 ; ρ   w 为水密度，取1.0 g/cm  3 ; ω 为泥沙沉速，cm/s; g 为重力加速度，取9.81 m/s  2 ; S  a  为沉速判数; ψ 为粒径判数。

粒径组平均沉速：

ω i  = ω iω  i+1   （7）

式中： ω  i  为粒径组平均沉速，cm/s; ω  i  为粒径组下限粒径沉速，cm/s; ω  i+1  为粒径组上限粒径沉速， cm/s 。

（2） 泥沙率计算。

各粒径组悬移质沉降率为

η  ik =1- e   -α i  ω —   iL k q k   （8）

q k= Q k B  （9）

式中： η  ik 为k池段粒径组沉降率;α  i 为恢复饱和系数;q  k  为池段单宽流量，m  2 /s; Q  k  为池段平均流量，m  3 /s，水电站定期冲洗式沉沙池为引用流量，连续冲洗式沉沙池为引用流量和冲沙流量之和; L  k  为池段长，m; B 为工作宽度，m，对于矩形断面沉沙池，为工作段闸室的净宽度，对于梯形断面沉沙池，可近似取正常水位以下的平均宽度。

恢复饱和系数：

α i=K （  ω —   i u * ）   0.25  （10）

u *= nv g  R  1/6   （11）

式中： u   * 为摩阻流速，m/s; ω —   i  为粒径组平均沉速， cm/s ; K 为综合经验系数，一般取 K =1.2; v 为断面平均流速，m/s; R 为池段平均过水断面水力半径，m; n 为池壁糙率; g 为重力加速度，m/s  2 。

不小于 i 粒径级的沉降率为

η l=   l  i=m  η i Δ P i   l  i=m   Δ P i  （12）

式中：l为第i粒径组下限粒径编号，按粒径由大到小排列; Δ P  i 为第i粒径组沙重百分数 ，%。经计算，在沉沙池计算长度为125.0 m时，沉沙池内粒径不小于 0.2 mm 泥沙沉降率为97.8%，满足设计要求。

（3） 计算结果。

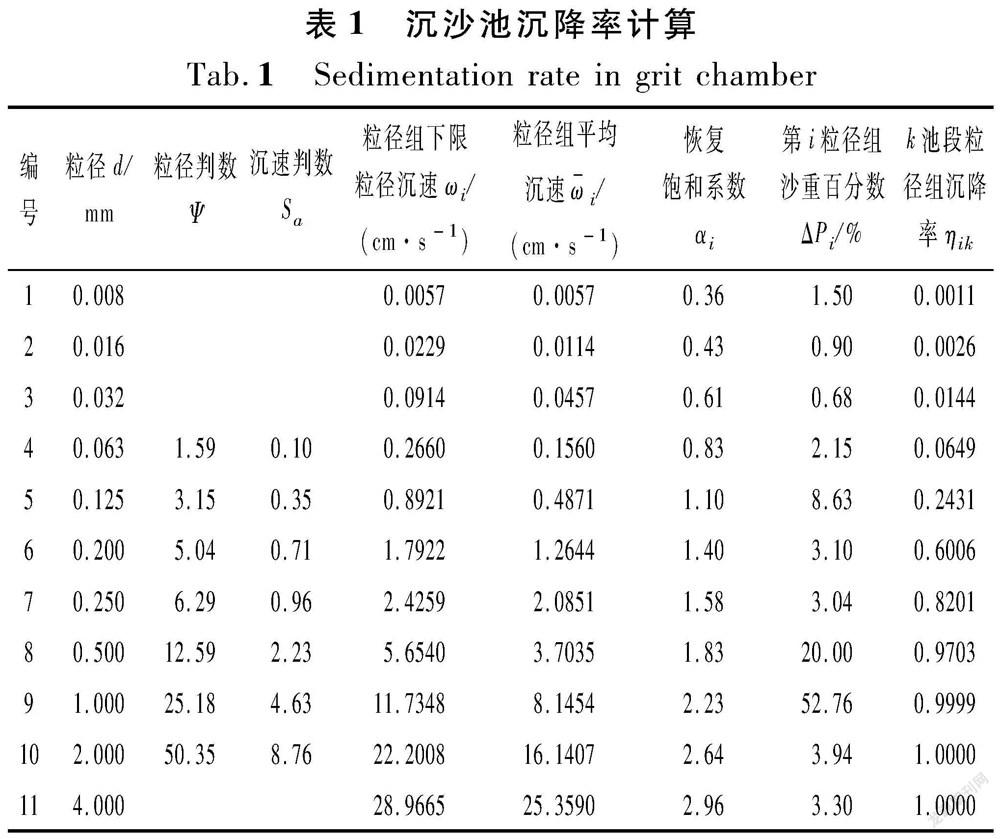
沉沙池沉降率计算结果见表1。

3 数值模拟

3.1 控制方程

水沙两相流模型基于连续介质假设，将颗粒相作为连续相处理。两相均由各自的连续性方程和动量方程描述，两相相互作用通过相间作用力耦合，本文采用质量平均来处理。流经沉沙池内的流体假设为不可压缩的牛顿流体，本次研究的连续方程和动量方程分别为

ρ  t +  ρ U i    x i =0 （13）

ρ U i    t +  ρ U iU j    x j =-  P -   x i +

x j   μ+ρυ T     U i    x j +   U j    x i   +ρg i （14）

υ T=C μ k 2 ε  （15）

式中：t表示時间， U i  表示 U  i方向的平均速度i=（1，2，3，…，n），P - 为平均压力，ρ为流体密度，g  i 为不同方向的重力加速度，k为紊流动能，ε为紊流动能消散率，μ为水分子黏性系数，υ  T 为紊流运动黏性系数，C  μ = 0.0085 ，为半经验系数。

3.2 紊流模型

本文基于大型流体计算软件CFX对沉沙池的含沙水流进行数值模拟。目前连续相湍流模型中最具代表性的两方程模型是标准 k～ε 模型，然而由于水沙两相流的不均匀性，水相与泥沙相之间的相互作用又难以精确模拟，本次紊流模型选用以控制方程的时间平均形式和RNG  k～ε 湍流模型来实现雷诺应力的封闭。RNG  k～ε 模型是由一种严谨的统计方法即重整化群理论推导出的，它与Standard  k～ε 湍流模型保持形式上的一致并有所改进，在其 ε 方程中增加了额外项，这样显著提高了快速应变流动的准确性。

3.3 数学模型

沉沙池几何模型极其复杂，难点之一是几何尺度跨度非常大且不规则，需进行必要的简化。本次研究采用MS来建立沉沙池三维模型。模型简化如图3所示。

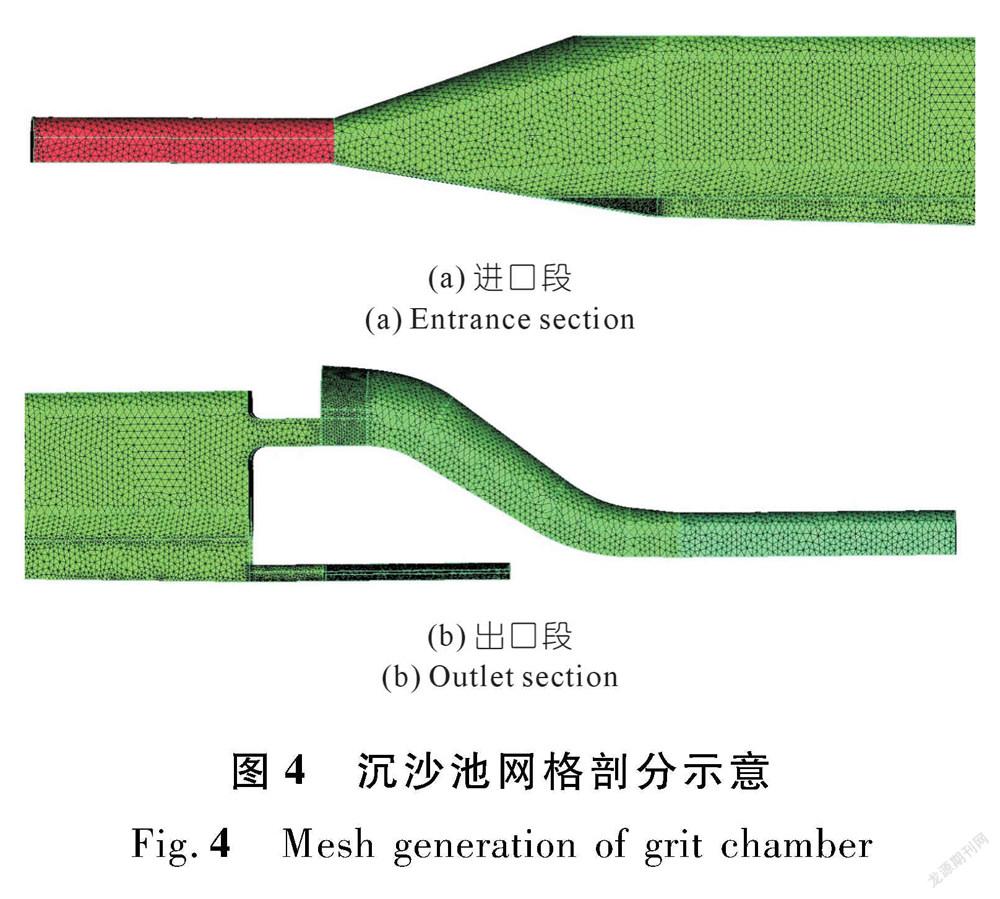
模拟高浓度泥沙沉积过程，需要同时求解泥沙和水的连续性方程和动量方程，因此计算量很大。网格划分原则是首先保证网格尺寸均匀过渡，不会使计算因网格纵横比太大而出现流量不守恒。其次，为保证泥沙沉降计算的稳定性，需选择合适的计算时间步长来确定网格尺寸。经过多次尝试，在保证Courant Number最大值在40上下波動的情况下，选择全局网格最大尺寸为1 200 mm，进口段最大为650 mm，进口截面最大为400 mm，沉沙池底部最大为450 mm，沉沙池尾部最大为650 mm，排沙管最大为350 mm。网格采用正四面体网格，网格单元为 2 035 047 ，网格节点数为396 739，最大纵横比14，最小角度16°，最小行列式值0.8。模型划分网格节点如图4所示。

3.4 边界条件

3.4.1 进口边界条件

（1）  入口流速。

水相和泥沙相均采用相同的入口流速条件。平行于进口边界的速度为零，垂直于进口边界的流速由窦国仁明渠流速度分布公式给定：

U U *      inlet  =2.5 ln  1+y * +7.05   y * 1+y *    2+

2.5  y * 1+y *  -B *+0.55 1- cos  2 π  y H    （16）

式中：y为垂向高度;U  * 为摩阻流速;B  * 为壁面粗糙度对流速分布的影响，y *=ρU *y/sμ，本次计算分析中壁面糙率在粗糙区，B  * 取值为2.3，H为明渠流水深。

（2） 入口体积分数。

进口边界水相体积分数为

r  w      inlet  =1-  r  s      inlet   （17）

r  s = S  w  ρ  s   （18）

式中： r   w  为水相体积分数，r   s  为泥沙相体积分数，S   w  为泥沙浓度，ρ   s  为泥沙密度。本次计算分析中取进口流量Q =36.67 m  3 /s，因此泥沙相体积分数 r   s =5.6/2650×100%=0.2113%

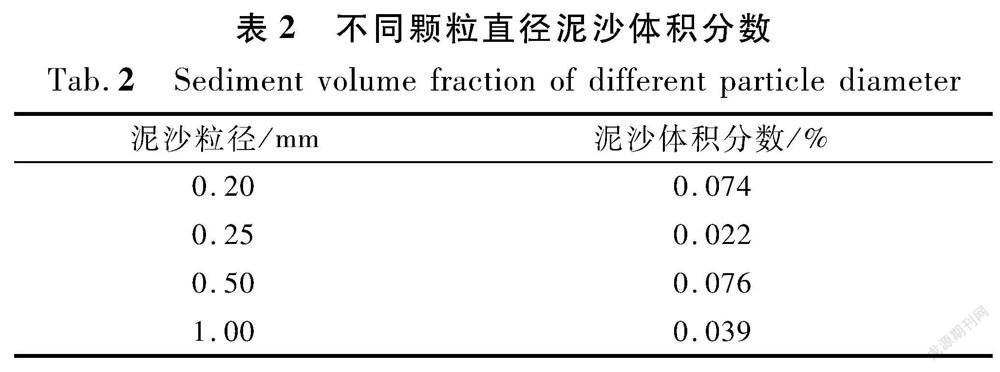
本次研究主要选取0.20，0.25，0.50，1.00 mm 4种颗粒级配泥沙粒径，不同粒径泥沙的体积分数如表2所列。

3.4.2 出口边界条件

（1） 出口压力。

水沙两相出口平均静压均为零。

（2） 出口湍流。

因流动为充分发展的湍流，出口给定湍动能和耗散率零梯度边界条件，即湍动能和耗散率沿出口方向一阶导数为零。

（3） 出口浓度。

沉沙池应满足平衡输沙条件，出口浓度边界条件给定垂直于出口边界的两相体积分数方向导数为零。

3.4.3 自由表面边界

因数学模型考虑重力，本次研究采用VOF体积分辨率函数来追踪自由表面。

3.4.4 壁面边界条件

壁面采用无滑移边界条件，即壁面上两相速度均为零。

3.5 结果分析

3.5.1 泥沙沉积率

本次研究采用多组分泥沙颗粒模型对沉沙池沉沙效果进行分析计算，由于很难单纯直接对多组分泥沙颗粒沉沙率进行查看，故采用含沙水流中泥沙体积分数变化率来反映沉沙池中泥沙沉降效果。某颗粒粒径的泥沙沉降率用 η 表示：

η= 1- V   outlet   V   inlet    ×100 %  （19）

式中：V   outlet  表示某粒径出口泥沙体积分数;V   inlet  表示某粒径进口泥沙体积分数。

3.5.2 沉沙池不同颗粒直径泥沙沉积效果

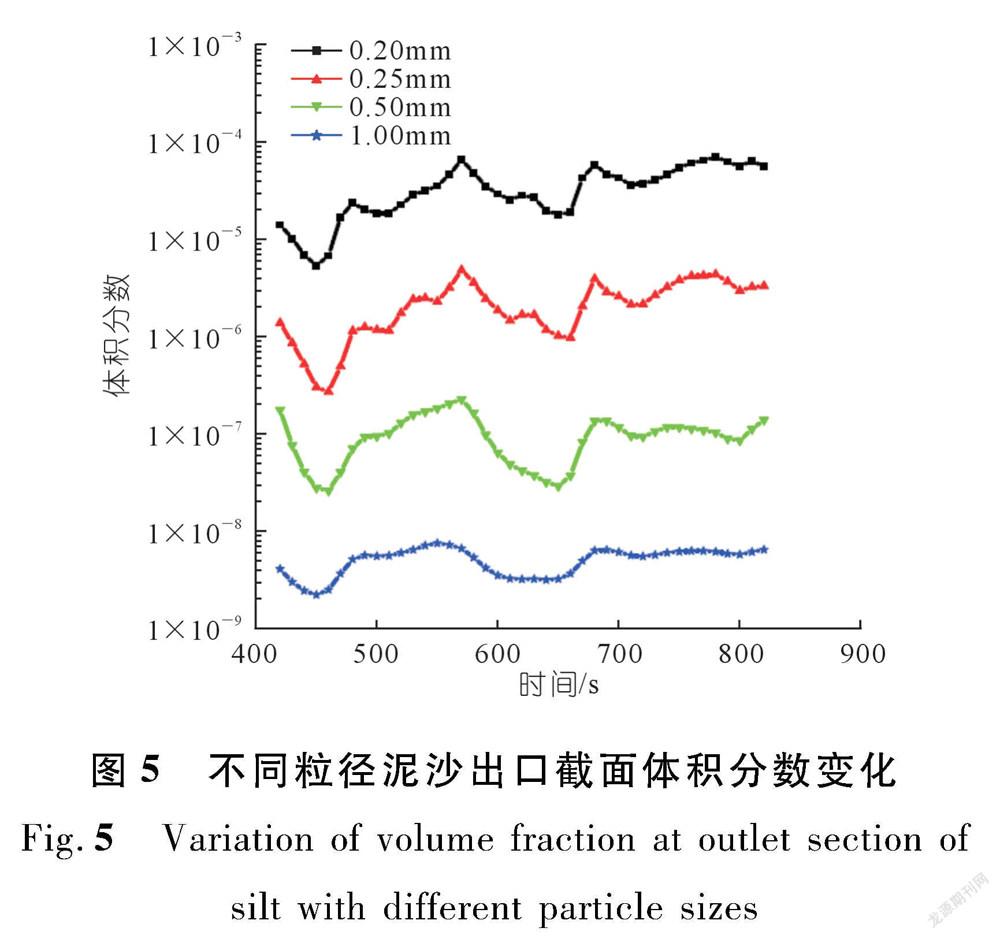
为了达到更好的收敛效果，本次计算时间步长取为0.5 s，在650～800 s时基本达到动态平衡稳定状态。为更精细地了解泥沙的沉降情况，以沉沙池出水口截面的泥沙平均浓度的体积分数为监测点，分析不同粒径泥沙体积分数随时间的变化，其变化趋势如图5所示。

根据出水口截面泥沙体积分数在不同时刻变化情况计算得出泥沙的沉降率，不同颗粒直径泥沙随时间变化的沉降率如表3所列。

计算成果表明：沉沙池内水流含沙量沿垂线分布是上小下大，即水流含沙浓度接近池底最高，在水面含沙量最低，符合泥沙的运动扩散规律;且通过以上计算对比可知，不同粒径泥沙的沉沙率均满足设计要求。相关研究表明：混合泥沙中粗颗粒对细颗粒有一定的遮蔽效应，即与等粒径的均匀泥沙颗粒相比，混合泥沙中同等粒径的细颗粒由于受到粗颗粒的制约而沉降更快。沉沙池进口区域受水流紊动影响，有轻微的絮凝现象发生，符合泥沙沉淀一般规律。

4 结 论

（1） 基于传统理论分析，结合国内外研究学者总结得出的沉沙池中含沙水流泥沙颗粒沉降理论，推导 出该水电站沉沙池不同颗粒直径泥砂的沉沙率，其中不小于0.2 mm颗粒直径泥沙沉降率为97.8%，满足工程设计要求。

（2） 数值模拟计算结果表明：该工程不小于0.2 mm粒径泥沙沉积率为95.59%，与理论分析结果较为吻合。而且数值方法还能模拟沉沙池冲砂效果，比理论分析方法更直观。

参考文献：

[1]  袁晶，许全喜，童輝.三峡水库蓄水运用以来库区泥沙淤积特性研究[J].水力发电学报，2013，32（2）：139-145.

[2] 王普庆.小浪底水库运用初期库区泥沙淤积分布特征[J].人民黄河，2012，34（10）：26-28.

[3] 廖庭庭，陈和春，高甜，等.三峡水电站过机泥沙粒径对水轮机叶片空化空蚀的影响[J].中国农村水利水电，2012（2）：121-124.

[4] DUBOYS M P.One dimensional bed wave movement in lowland rivers[J].Water Resources Research，1983，19（3）：627-631.

[5] ROUSE H.Experiments on the mechanics of sediment suspension[C]∥Proceedings of the 5th International Congress for Applied Mechanics，Cambridge，1939：550-554.

[6] 窦国仁.论河流紊动与流速分布[J].水利学报，1959，5（4）：49-50.

[7] 蔡树棠.泥沙对水的相对速度和含沙浓度对脉动速度的影响[J].应用数学和力学，1982，3（1）：1-10.

[8] 杨红，潘光在.沉沙池立面流场数值模拟研究[J].泥沙研究，2000，18（2）：55-59.

[9] 胡斌，桂林.斜板式沉沙池水流流态数值模拟[J].西南民族大学学报（自然科学版），2012，38（3）：425-430.

[10]  周晓泉.复杂边界条件下的三维紊流数值模拟研宄[D].成都：四川大学，2003.

[11] 张军，侍克斌，高亚平，等.圆中环沉沙排沙池流场三维数值模拟研究[J].水力发电学报，2015，34（3）：103-110.

[12] 岳竹，肖钰.有压隧洞内沉沙池泥沙沉降特性研究：以尼泊尔尼亚迪水电站为例[J].人民长江，2020，51（增1）：200-203.

[13] CHEN Q，DAI G，LIU H.Volume of fluid model for turbulence numerical simulation of stepped spillway overflow[J].Journal of Hydraulic Engineering，2002，128：683-8.

[14] 朱鉴远.水利水电工程泥沙设计[M].北京：中国水利水电出版社，2010.

（编辑：胡旭东）

Study on sand depositing and sand flushing effect in grit chamber of  Rasuwagadhi Hydropower Station

GAO Donghong，ZOU Hao

（ Shanghai Investigation，Design & Research Institute Co.，ltd.，Shanghai 200434，China ）

Abstract：

In water conservancy and hydropower projects，a grit chamber is generally used to reduce the sediment content，so as to reduce the adverse impact of the sediment on the water diversion and power generation system.It is very important to study the flow pattern of sand-containing water flow，sand depositing and sand flushing effect in the sand grit chamber.Based on a grit chamber of Rasuwagadhi Hydropower Station，using the theoretical formula，RNG  k～ε  turbulence model and volume resolution function VOF，we simulated the flow pattern of the two-phase flow of sediment in the grit chamber，and showed the deposition effect of different sand particle in the multi-diameter particle composition in detail.The results showed that the sand depositing efficiency of no less than 0.2 mm was more than 95%，and the numerical results agreed with the theoretical calculation and met the engineering design requirements.

Key words：

grit chamber;sand depositing efficiency;numerical simulation;Rasuwagadhi Hydropower Station;Nepal