基于GRAPES-GFS 次季节预报的误差诊断和预报能力分析

齐倩倩 朱跃建 陈静 田华 佟华 2

1 中国气象局地球系统数值预报中心，北京 100081

2 国家气象中心，北京 100081

3 美国国家海洋和大气管理局/国家气象局/国家环境预报中心/环境模式中心，马里兰大学帕克分校，美国20742

1 引言

次季节尺度的天气预报是对某一地区未来几周的天气状况进行预测，它衔接了天气预报（1～10 d）和气候预测（月尺度以上）的“时间缝隙”，在防灾减灾决策服务中起着重要作用。然而，目前的气象业务其天气预报的有效预报时长通常是10 天左右，两周至一个月之间的次季节预报一直是天气预报业务的空白领域，备受科学研究和业务预报的关注。欧洲中期天气预报中心（European Center for Medium range Weather Forecasts，简称ECMWF）指出，高影响天气事件的有效预报时效在未来10年将提升至2 周，大尺度环流形势及转折的预报时效提升至超前4 周（ECMWF, 2016）。美国国家科学院（National Academy of Sciences, NAS）制定了延伸期预测研究计划，提出未来将次季节预测应用提升至目前天气预报的预报水平（Black et al.,2017）。美国国家海洋大气局（National Oceanic and Atmospheric Administration，简称NOAA）计划发展次季节到季节尺度的预报系统，并提供超前3～4 周的预报服务（Zhu et al., 2017）。中国气象局在“智能网格预报行动计划（2018～2020 年）”中，也明确提出将常规气象要素和重要天气过程的次季节预报列为未来天气预报研究的重点任务和攻关的关键核心技术。

全球各大数值预报中心相继利用大气环流模式开展延伸期次季节预报试验。美国国家气象中心开展了冬、春两季每月30 天的逐日数值预报试验（Tracton et al., 1989）。ECMWF 开展了逐月的延伸期预报试验，加拿大和日本也进行了类似的试验（Palmer, 1993; Yamada et al., 1991）。各数值天气预报中心对大气环流模式的预报评估结果显示，大气环流模式仅依赖于初值信息，其对前7～10 d 大尺度环流形势的预报能力决定了更长时间的预报效果。Zhu et al.（2018）基于NCEP 全球集合预报系统（NCEP GEFS），评估了海表温度（SST）强迫对3～4 周各天气要素次季节预报性能的影响，结果表明，更实时的SST 强迫方案可提高热带大气振荡（MJO）预报技巧，但对2 m 温度和降水预报技巧提高不大。进一步地，Li et al.（2019）采用NCEP 全球集合预报系统（NCEP-GEFS），基于4 种不同的集合预报试验方案，指出改进随机物理扰动方案、采用新的对流化方案及更新实时SST方案，可极大地提高热带大气振荡（MJO）的次季节预报技巧。

GRAPES（ Global/Regional Assimilation and Prediction System）全球预报系统（GRAPES Global Forecast System，简称GRAPES-GFS）是由中国气象局数值预报中心自主研发的多尺度通用资料同化和数值预报系统（王金成等, 2017），该系统在2016 年6 月实现业务化运行（刘永柱等, 2013），目前已建立了一套针对日常业务应用的完善的预报性能常态化检验反馈机制。基于新版本的GRAPES-GFS 模式，沈学顺等（2017）对各等压面要素的中期预报能力进行了综合评估。宫宇等（2018）从天气学角度评估了GRAPES-GFS 模式对不同季节、不同区域及不同尺度影响系统的暴雨过程的预报能力。张萌等（2018）通过对比GRAPES-GFS 2.0 预报产品和NCEP FNL 分析资料，对GRAPES-GFS 模式的系统误差做了综合分析。以上这些工作主要基于GRAPES-GFS 模式，对其中期预报性能进行评估，然而，对于其延伸期次季节预报性能的分析和诊断工作鲜有开展。

大气作为一个复杂的非线性系统，其本身固有的混沌特征是数值天气预报模式进一步发展的主要制约因素，尤其对于时间尺度在两周以上的延伸期次季节预报，目前仍缺少可用于业务的预报技巧。然而，数值天气模式在长期的预报过程中所表现出的预报技巧及预报误差的稳定性、相似性，可对较长时间的预报提供有用的信息。因此，需要将数值模式的次季节预报产品与不同的再分析资料进行比较，给出预报要素的预报技巧和预报误差的时空分布，从而找出模式存在的系统偏差，为数值天气模式延伸期次季节预报的发展提供指导。

本文对次季节尺度预报性能进行评估的主要物理量是：温度、位势高度和热带大气季节内振荡（MJO）。2 m 温度是地面要素的常规物理量，可作为衡量不同模式分析资料差异及评估系统性能偏差的重要指标，因此，关于地面要素，本文着重对2 m 温度进行分析。由于500 hPa 位势高度场受下垫面影响相对较小且环流形势较为稳定，可以描述大尺度天气特征，是数值预报系统的主要关注对象，因此，关于高空要素，本研究重点分析500 hPa位势高度场。此外，MJO 作为热带大气季节内变率的主要模态，经过印度洋和太平洋，向东移动并绕 行 全 球，具 有 准 周 期 性（Madden and Julian,1971, 1972）。同时，MJO 与热带地区的对流活动有密切关系，且其时间尺度介于月、季之间，不仅对热带地区，还对中高纬地区的天气气候有显著影响（He et al., 2011; Jia et al., 2011; 冯俊阳和肖子牛,2012, 2013）。因此，本研究也对MJO 进行诊断分析和预报评估。结合以上分析，本研究试图采用中国气象局数值预报中心自主研发的GRAPES 全球预报系统，开展次季节尺度的可预测性研究。通过对该预报系统的常规要素（气温、环流）和重要天气过程MJO 的次季节预报效果进行诊断分析，可有效获取模式预报性能、判定系统性误差分布特征，为GRAPES-GFS 模式进一步改进和发展提供思路。

2 GRAPES-GFS 模式试验配置及选用资料

GRAPES-GFS 模式的动力框架采用非静力平衡的动力方程组及采用半隐式—半拉格朗日方法做时空离散。物理过程方面，辐射选用RRT-MG LW(V4.71)/SW(V3.61)方案（Iacono et al., 2000），陆面过程为通用陆面模式CoLM（Hong and Pan,1996; Dai et al., 2003），微物理过程选用中国气象局研发的CMA 双参数方案（Lott and Miller, 1997），并引入次网格尺度地形重力波参数化。在本研究的积分试验配置中，模式积分的区域为全球，水平分辨率为50 km，即0.5°×0.5°，垂直层数输出为60 层。模式积分的初始分析场通过GRAPES 4 维变分（4-Dimension Variational Assimilation，简称4DVAR）同化方法获得（王金成等, 2017）。对于每次预报，采用NCEP 的最优插值（Optimal Interpolation，简称OI）海表温度（SST）日平均再分析资料作为强迫场输入到模式中，该资料在模式积分过程中固定不变。

本文采用的分析时间段为2018 年9 月1 日至2019 年8 月31 日，跨2018 年秋季、冬季和2019年春季、夏季。具体地，采用GRAPES-GFS 模式积分，起报时间选用分析时间段内逐7 天间隔的00:00（协调世界时，下同）和12:00。即，2018年9 月1 日分别在00:00 和12:00 开始预报，2018年9 月8 日分别在00:00 和12:00 开始预报，2018年9 月15 日分别在00:00 和12:00 开始预报，依次类推。对于每个时次的预报，积分时长为35 d，预报输出结果间隔为12 h。

首先，对模式输出结果做后处理，通过插值转换和多要素综合计算，将非规则格点的数据、非等压面数据插值到等经纬度网格和等压面上，生成Grib2 格式的等压面数据。具体地，对于云量、云水物质等要素采用线性插值方法，对于垂直风、高度和温度等要素采用三次样条插值方法，对于水平方向要素采用双线性插值方法，从而将这些模式输出结果从模式垂直坐标垂直插值到预报员熟悉的等压面坐标。

作为对照，本文使用的2 m 温度数据分别为NCEP/NCAR 及ECMWF 所发布的同时间段的再分析资料。其中，下载的NCEP/NCAR 资料为日平均再分析资料，下载的ECMWF 再分析资料，将每天2 个时次（00:00 和12:00）的结果进行平均得到。本文使用的500 hPa 位势高度场为NCEP/NCAR发布的日平均再分析资料。在检验MJO 预报技巧时，采用的850 hPa 和200 hPa 纬向风场（U850和U200）数据为NCEP/NCAR 所发布的日平均再分析数据；大气层顶层对外长波辐射（Outgoing Longwave Radiation，简称OLR）数据为NOAA 发布的同时间段的日平均再分析数据；用于衡量本文计算的MJO 指数（RMM）准确性的标准是由澳大利亚气象局提供的，利用实时多变量计算的RMM（http://www.bom.gov.au/climate/mjo/ [2019-12-01]）。

3 诊断分析及预报检验方法

3.1 空间距平相关（PAC）

空 间 距 平 相 关 PAC（ Pattern Anomaly Correlation）主要反映的是预报距平值与实况距平值空间型的相似程度，每次预报均可对预报计算空间相似系数，通常用于检验空间场（Murphy and Epstein, 1989）。PAC 是在空间场的检验方面广为使用的一种度量，它是预报距平和观测距平间的相关系数，其表达式如下：

其中，

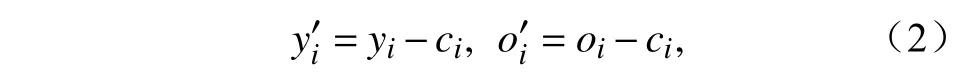
式中，yi和oi分别是预报和观测在网格点i处的值，ci是 气候态,y和o分别是预报距平和观测距平，和分别是预报距平和观测距平场的空间平均。本文中，PAC 估计了预报和分析场（在此是“truth run”）之间的距平相关，PAC 越大，预报技巧越高。

3.2 均方根误差（RMSE）

RMSE 通常用于评估预报和观测间的平均差别，其表达式如下：

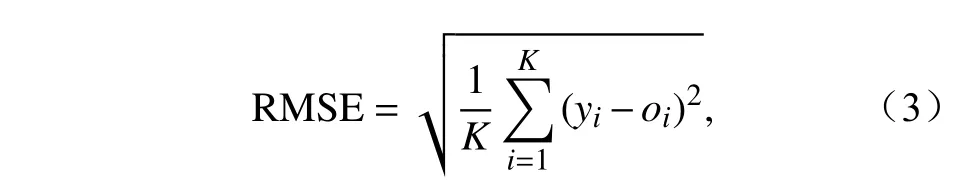
其中，K是空间网格点个数。本文中，RMSE 度量了预报场和同一时间分析场之间的差，RMSE 越小，预报越准确。

3.3 时间相关系数（TCC）

时间相关系数能够在统计意义上较好地表征数值模式对每个空间格点要素的预报能力，从而得到一个完整的相关技巧的空间分布。通过计算时间相关系数TCC,可给出要素在选取时间段内每个空间格点的预报技巧。在计算TCC 时，需要求出每个格点要素的均方差和协方差，其表达式如下：

其中，xi,j表 示观测值，fi,j表示预测值，i=1,2,3,···,M表示所选区域的格点数，j=1,2,3,···,N表示时间序列；S(xi)表 示观测值的标准差；S(fi)表示预测值的标准差；S(xi,fi)表示预测值和观测值的协方差。

3.4 合成主成分分析（CEOF）方法

EOF 是大气和海洋资料分析中常用的多变量分析方法之一，用来揭示一个要素场的主要时空特征（魏凤英, 2007）。其基本原理是：将m个变量的n次观测资料场表示成如下的矩阵形式：

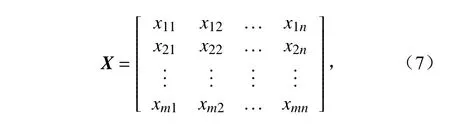
其中，矩阵中元素xij(i=1,2,···,m;j=1,2,···n)表示变量xi在 时刻j的观测值。进一步，将矩阵X分解为空间函数vik和 时间函数yki的线性组合，即

对于资料矩阵X，按照上述方法分解成矩阵的形式，可表示为

其中，V为空间函数矩阵，Y为时间函数矩阵，即

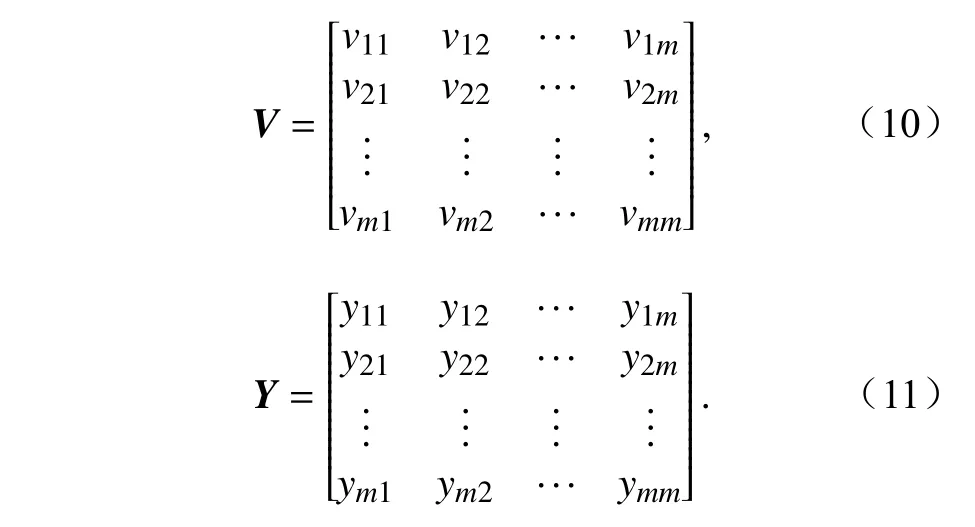
在该分解过程中，要求不同的空间函数保持正交，即要求：

最后，通过求解矩阵XXT的特征向量从而得到空间函数V以及计算Y=VTX得到时间函数。

通过EOF 分析，一方面，可将变量分解为与空间无关的时间函数和不随时间变化的空间函数，以便进行时空特征的分析；另一方面，按照解释方差的大小对分解得到的空间函数和时间函数进行组合排列，根据需要可选取排名前几的时空函数的组合以反映变量的主要特征。在本研究中，为评估MJO的预报能力，我们将赤道地区（15°S～15°N）20天季节内带通滤波和标准化处理后的OLR、200 hPa和850 hPa 纬向风进行合成EOF，称为合成EOF（CEOF），取前两个主分量，以获取RMM 指数。

4 预报效果分析

4.1 不同分析资料的比较

本文选取了2018 年冬季（2018 年11 月、12月及2019 年1 月）和2019 年夏季（2019 年6 月、7 月、8 月）的2 m 温度和500 hPa 位势高度场为例进行分析。首先，将GRAPES-GFS 分析场的2 m温度日平均与其它两套分析资料（NCEP/NCAR 和ECMWF 再分析资料）进行对比，从而对GRAPESGFS 模式性能做初步评估。结果表明，GRAPESGFS 模式可基本反映出全球2 m 温度在热带、北半球热带外和南半球热带外的空间分布，并能反映出全球2 m 温度的纬向梯度和经向梯度的分布特征，如图1。进一步地，为了衡量不同资料分析场的相似程度，我们将采用相似系数来度量。相似系数的

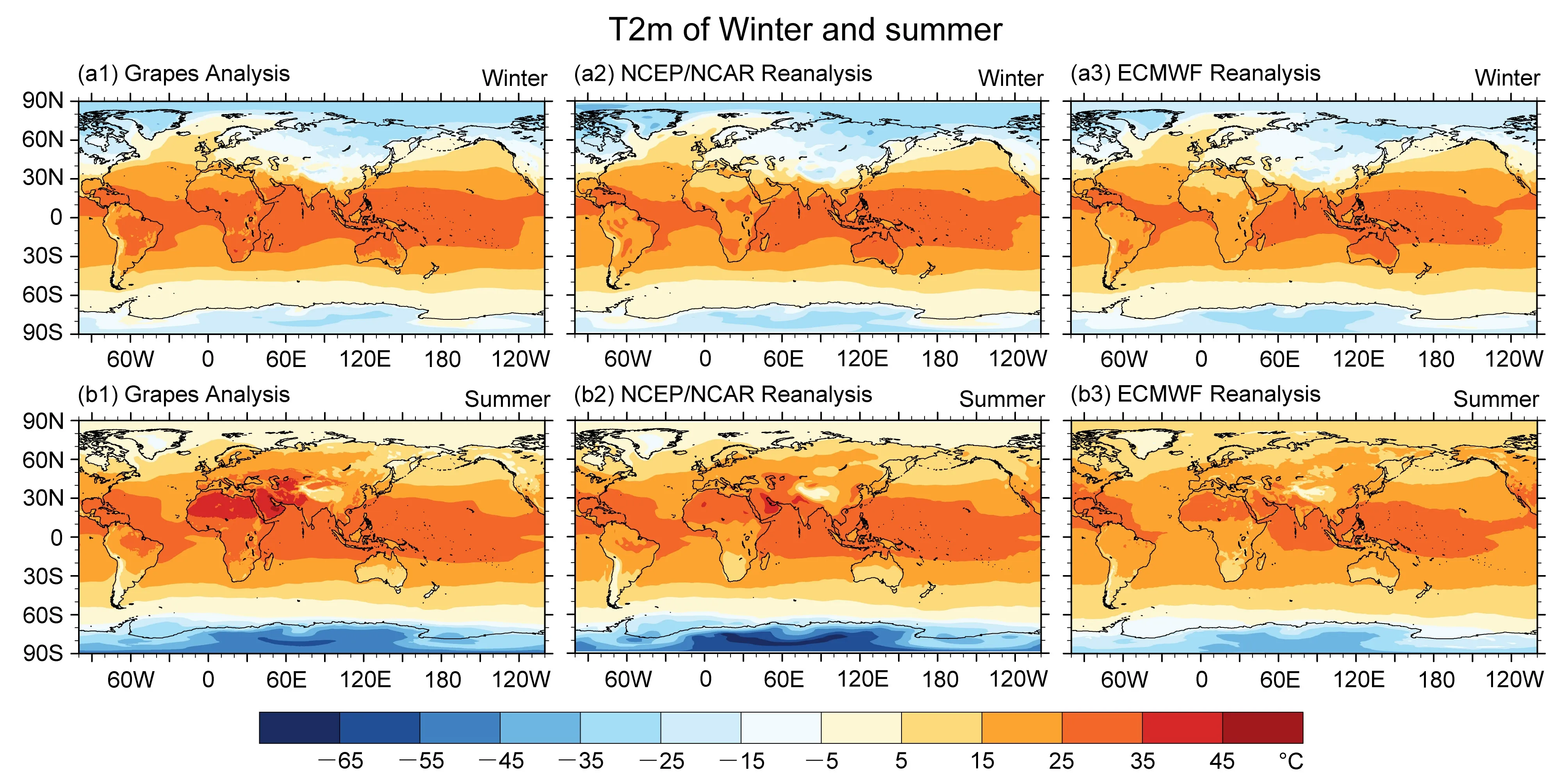
图1（a1–a3）2018 年冬季（2018 年11 月、12 月及2019 年1 月）和（b1–b3）2019 年夏季（2019 年6 月、7 月、8 月）全球季节平均的2 m 温度（单位：°C）分布：（a1、b1）GRAPES-GFS 分析场；（a2、b2）NCEP/NCAR 再分析资料；（a3、b3）ECMWF 再分析资料Fig.1 The distribution of the global seasonal average of daily 2-m temperature (units: °C) from (a1, b1) GRAPES-GFS, (a2, b2) NCEP/NCAR reanalysis, and (a3, b3) ECMWF reanalysis during the winter (Nov–Dec–Jan) in 2018 and summer (Jun–Jul–Aug) in 2019, respectively

计算公式如下（Kim et al., 2004; Buizza et al., 2005）：

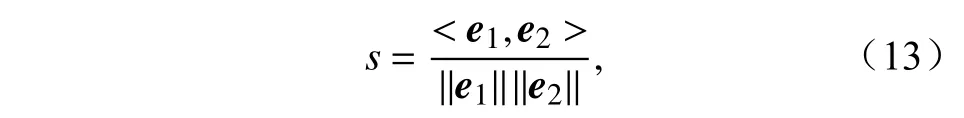
其中，er表示第r个空间场，是不同空间场er和et的 内积，且//er//=,r=1,2。

通过计算GRAPES-GFS 与其他分析资料在不同季节的相似系数s，结果表明，GRAPES-GFS 与其它两套分析资料相比，在冬季空间相似系数普遍高于夏季，这可能与夏季地面温度变化剧烈，模式不容易准确地预报出有关。另外，无论是冬季还是夏季，GRAPES-GFS 与NCEP/NCAR 分析资料的空间相似程度更高（表1）。

表1 GRAPES-GFS 与其他分析资料的2 m 温度在不同季节的相似系数Table1 Similarity coefficients of seasonal-mean 2-m temperatures between three groups of analysis/reanalysis data

从误差的角度上，与NCEP/NCAR 及ECMWF再分析资料相比，无论是冬季还是夏季，GRAPESGFS 模式的2 m 温度在非洲大陆及欧洲大陆大部分地区呈现暖偏差，在北美洲及澳大利亚地区呈现冷偏差，其中，与ECMWF 再分析资料相比，偏差更为显著，如图2。另外，GRAPES-GFS 模式与其它两套分析资料相比，夏季误差比冬季误差更大，且受海陆分布与地形分布差异影响较大，陆地比海洋区域误差更大。进一步地，图3 为不同分析资料（GRAPES-GFS、NCEP/NCAR、ECMWF）对中国东南区域及非洲干旱区2 m 温度的时间序列。三套分析资料的2 m 温度随时间发展的变化趋势基本保持一致，然而，与其它两套分析资料相比，GRAPES-GFS 分析场在非洲干旱区误差显著增大，且在非洲干旱区，2 m 温度始终比其它两套分析资料偏高，夏季更为明显。这表明，在热力强迫作用显著的非洲干旱区，地面2 m 温度正偏差非常大。造成这种系统偏差的可能原因，一方面是因为非洲干旱地区地面热容量小，昼夜温差特别大，GRAPES-GFS 模式常常不能准确地刻画出日变化剧烈的温度；另一方面，非洲干旱区地面资料缺少，地形资料分辨率低，因此在近地面处，2 m 温度存在较大的误差。在未来模式改进方面，需要进一步增加非洲干旱区的地面资料，提高地形资料分辨率，同时完善全球陆面系统同化，GRAPES-GFS 对地面要素的效果有可能会进一步增加。

图2 2018 年冬季（左列）和2019 年夏季（右列）全球2 m 温度的季节平均的偏差分布（单位：°C）：（a1、a2）GRAPES-GFS 与NCEP/NCAR 之差；（b1、b2）GRAPES-GFS 与ECMWF 之差Fig.2 The distribution of the global seasonal average error of daily 2-m temperatures (units: °C): (a1, a2) Difference between GRAPES-GFS and NCEP/NCAR; (b1, b2) difference between GRAPES-GFS and ECMWF during the winter in 2018 (left column) and summer in 2019 (right column)

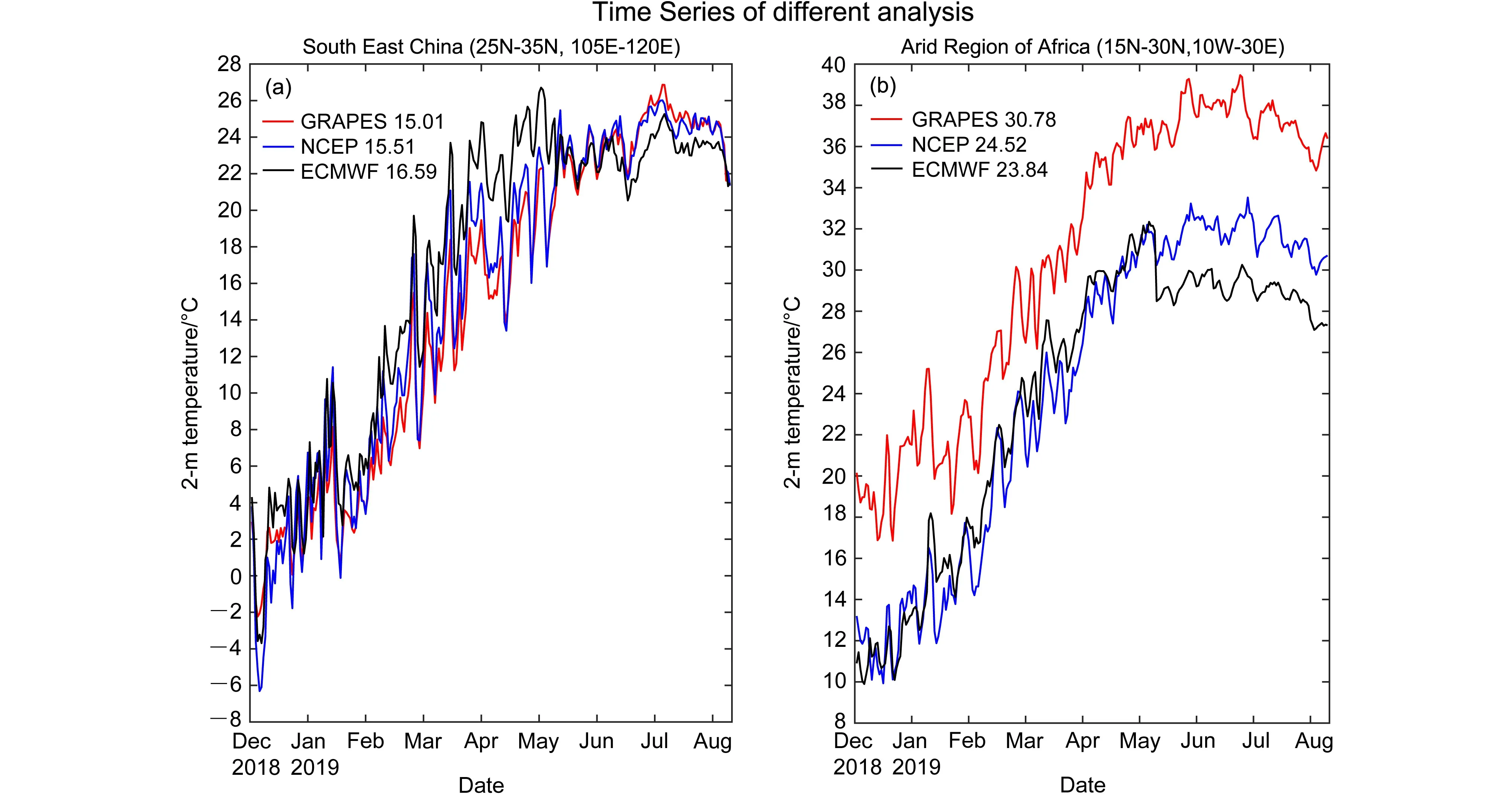
图3（a）中国东南区及（b）非洲干旱区日平均2 m 温度的时间序列（单位：°C）。其中，不同颜色的曲线代表不同分析资料的2 m 温度序列，标签中的数字表示全部月份2 m 温度的平均值Fig.3 Time series of daily 2-m temperature over (a) South East China and (b) arid region of Africa (units: °C). The different colour lines indicate the daily 2-m temperature series with different analysis data. The numbers in the legends indicate mean 2-m temperature of the whole reforecast period

500 hPa 位势高度场处于对流层中部，受地形影响较小，通过对2018 年冬季和2019 年夏季500 hPa位势高度的季节平均诊断，结果表明：GRAPESGFS 模式可基本反映出500 hPa 位势高度在南北的纬向梯度差异，即热带和副热带地区位势高度整体较高，两极地区位势高度整体较低，呈现出较明显的条带状分布，且夏季位势高度整体高于冬季（图4）。进一步地，相比于NCEP/NCAR 再分析资料，在2018 年冬季和2019 年夏季，误差在南北半球中纬度地区均呈现波列状分布，且大值区域正负偏差交替出现，无较明显的海陆分布和地形分布差异。另外，冬季偏差要大于夏季，高纬度地区偏差大于低纬度地区。同样地，对于500 hPa 位势高度，我们也计算了GRAPES-GFS 与NCEP/NCAR 再分析资料在冬季和夏季的空间相似系数s，分别为0.82 和0.91。这表明，GRAPES-GFS 的500 hPa 位势高度的空间分布与 NCEP/NCAR 再分析资料的空间分布在夏季比冬季更为相似。这可能是因为，冬季大尺度环流形势特征比较明显，变化较大，因此，不同模式之间的差异性也更为明显。

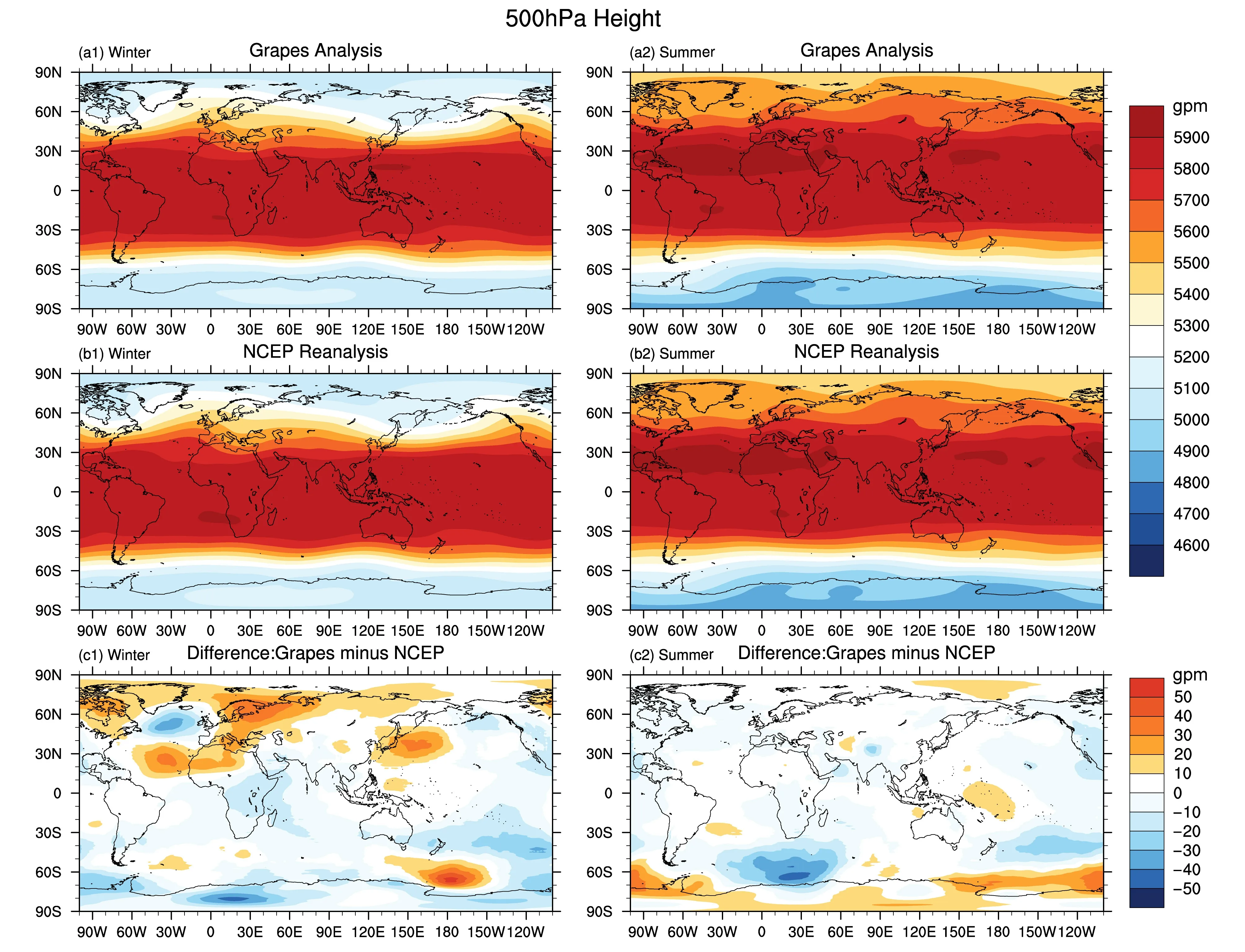
图4 2018 年冬季（左列）和2019 年夏季（右列）季节平均的（a1、a2）GRAPES-GFS 分析场以及（b1、b2）NCEP/NCAR 再分析资料的500 hPa 位势高度（单位：gpm）分布，（c1、c2）GRAPES-GFS 与NCEP/NCAR500 hPa 位势高度之差（单位：gpm）的分布Fig.4 Seasonal means of 500-hPa geopotential heights from (a1, a2) GRAPES-GFS, (b1, b2) NCEP/NCAR reanalysis and (c1, c2) their corresponding errors (units: gpm) during the winter in 2018 and summer in 2019, respectively

4.2 模式次季节预报的系统性能偏差

2 m 温度受海陆分布差异影响较大，尤其，4.1 节中，三套分析资料对比结果表明，2 m 温度陆面的误差远大于海洋区域，且相比于陆地，海表温度（SST）的日变化非常小。另外，GRAPESGFS 模式在预报时，对于SST 每天采用NCEP 的OI 分析资料更新一次，积分过程中不发生变化。因此，在诊断分析模式次季节预报的系统性能偏差时，我们将海洋区域的数据去掉，只探讨陆地区域的系统性偏差。图5 给出了在不考虑海洋区域数据后，GRAPES-GFS 模式2 m 温度分别超前预报1～4 周时相对误差（格点） (Fi−Ai)的空间分布。当GRAPES-GFS 模式超前1～4 周的预报结果与自身分析场相比时，相对误差大小在整个预报时效内逐渐增大；当超前预报1 周时，误差偏差大多不超过2 度，其正偏差大值区主要集中在东亚和澳大利亚地区；当超前更长时间（2～4 周）预报时，正偏差大值区主要集中在东亚、北美洲北部及欧洲大陆东部延伸区，而在非洲沙漠干旱区呈现弱的冷偏差，在澳大利亚沙漠区呈现弱的暖偏差。当与参考态为NCEP/NCAR 分析场相比时，相对误差明显增大，暖偏差大值区主要集中在非洲沙漠干旱区、德干高原和青藏高原等高原沙漠地区，而在澳大利亚沙漠区偏差较小。当与ECMWF 分析场相比时，其偏差的空间分布与NCEP/NCAR 作为参考态时类似，但相对误差大小值进一步增大。综合模式1～4 周预报结果与三套分析资料对比，当去除海洋区域后，模式次季节预报的系统性能偏差主要分布在热力强迫作用显著的高原沙漠地区，当在更长时间的预报后，该偏差程度更为明显。

图5 GRAPES-GFS 模式2 m 温度超前1～4 周（第一行至第四行）次季节预报平均的相对误差（单位：°C）：（a1–a4）参考态为GRAPES-GFS 分析场；（b1–b4）参考态为NCEP/NCAR 分析场；（c1–c4）参考态为ECMWF 分析场Fig.5 Relative errors (units: °C) of daily 2-m temperature sub-seasonal predictions for weeks 1, 2, 3 and 4 (from top line to bottom line): (a1–a4)With the reference field from the GRAPE-GFS analysis; (b1–b4) with the reference field from NCEP/NCAR reanalysis; (c1–c4) with the reference field from ECMWF analysis

4.3 GRAPES-GFS 地面和高空要素的次季节预报能力

4.3.1 地面2 m 温度（T2m）的次季节预报能力

对于地面要素2 m 温度，图6 给出了GRAPESGFS 模式对全球、北半球和东亚地区2 m 温度分别超前预报1 周、2 周、3 周和4 周均方根误差的时间序列，在此，计算均方根误差时，参考态选用的是GRAPES-GFS 的分析场。其中1 周的计算采用1～7 天的平均，2 周的计算采用8～14 天的平均，3 周是15～21 天平均，4 周是22～28 天平均。结果表明，随着预报时间的增加，RMSE 逐渐增加，且冬季的RMSE 要高于夏季，具有明显的季节依赖性。另外，随着预报时间增加，东亚的RMSE低于北半球和全球。均方根误差在超前1 周至2 周预报时效内近似于线性增长，而在超前2 周至4 周预报时效内逐渐趋于稳定。这说明，对于2 周以上的预报时效，2 m 温度的RMSE 逐渐趋于饱和，次季节预测值更加稳定。

图6 2018 年11 月至2019 年8 月, 去除海洋区域后，GRAPES-GFS 模式对全球、北半球和东亚陆地地区2 m 温度分别超前预报（a）1 周、（b）2 周、（c）3 周和（d）4 周时均方根误差的时间序列图。不同颜色的曲线代表不同区域的均方根误差序列，标签中的数字表示全部月份均方根误差的平均值Fig.6 RMSE of 2-m temperature forecasts over the global area (land only), Northern Hemisphere (NH) and East Asia (EA) for (a) leading 1 week,(b) leading 2 weeks, (c) leading 3 weeks and (d) leading 4 weeks during the period from November in 2018 to August in 2019. The different lines indicate the RMSE series over different regions and the numbers in the legends indicate the mean RMSE of the whole reforecast period

时间相关系数TCC 能够在统计意义上较好的表征模式对各个格点异常的预报能力，得到一个完整的相关技巧空间分布。图7 给出了2018 年11 月至2019 年8 月期间超前1 周至3 周预报时2 m 温度的预报技巧。从图中可看出，无论提前多长时间预报，赤道TCC 最低，北半球预报技巧高于南半球。在超前1 周和2 周预报时，2 m 温度预报技巧较高的区域主要位于两极、东亚及澳大利亚等地区，全球平均的TCC 值均在0.7 以上，在超前3 周和4 周预报时，2 m 温度的TCC 预报技巧进一步下降，但空间分布基本保持不变。和陆地相比，海洋区域2 m 温度的TCC 预报技巧较低，这可能与全球模式采用的海温设置有关。GRAPES-GFS 作为大气模式，其在试验配置时采用的是固定的SST，因此模式不能很好地描述海洋区域的海气耦合物理过程。而在海洋地区，大气的2 m 温度受海气相互作用影响较大，鉴于模式不能很好地刻画SST 与大气的反馈，所以2 m 温度的预报技巧在海洋区域较低。

图7 GRAPES-GFS 模式对2 m 温度超前1 至4 周预报的时间相关系数。(a) 超前预报1 周；(b) 超前预报2 周；(c) 超前预报3 周；(d) 超前预报4 周。其中，右标题的数字表示全球平均的TCC 技巧Fig.7 TCC (Temporal Correlation Coefficient) of 2-m temperature forecasts during weeks 1, 2, 3 and 4 for (a) leading 1 week, (b) leading 2 weeks,(c) leading 3 weeks and (d) leading 4 weeks. The numbers in the right title indicate the mean TCC over the global areas

4.3.2 高空500 hPa 位势高度场的次季节预报能力

对于高空要素500 hPa 位势高度场，图8 给出了超前1 周、2 周、3 周和4 周预报的全球、北半球和东亚地区500 hPa 位势高度场的PAC 预报技巧序列。由图8 可知，在超前1～3 周的预报时效内，PAC 预报技巧随预报时长近似于线性下降，超前4 周预报时，基本趋于稳定。另外，东亚的PAC 预报技巧随季节变化的波动较大，这可能是因为，500 hPa 位势高度场处于对流层中部，而东亚地区的中小尺度天气过程在不同季节变化很大，因而对500 hPa 位势高度场的预报技巧影响较大。另外，超前1～4 周预报的TCC 技巧在南北半球中纬度地区呈现散点状分布，无较明显的海陆分布和地形分布差异（图9）。在超前1 周预报时，500 hPa位势高度场预报技巧最高，平均在0.8 以上。当超前2 周预报时，技巧下降迅速，平均在0.57 左右，当超前更长时间的预报，预报效果较差。其中北半球预报技巧高于南半球，东亚的技巧相对其他区域较高，尤其是东亚中低纬度地区预报技巧明显高于中高纬度地区，热带地区的预报技巧远低于其它地区。

图8 2018 年11 月至2019 年8 月, GRAPES-GFS 模式对全球、北半球和东亚地区500 hPa 位势高度场分别超前预报（a）1 周、（b）2 周、（c）3 周和（d）4 周PAC 技巧的时间序列。其中，不同颜色的曲线代表不同区域的空间距平相关PAC 预报技巧序列，标签中的数字表示全部月份PAC 预报技巧的平均值Fig.8 The PAC (Pattern Anomaly Correlation) time series of 500-hPa geopotential height forecasts during weeks 1, 2, 3 and 4 over the global area,Northern Hemisphere (NH) and East Asia (EA) for (a) leading 1 week, (b) leading 2 weeks, (c) leading 3 weeks and (d) leading 4 weeks during the period from November in 2018 to August in 2019. The different lines indicate the PAC series over different regions and the numbers in the legends indicate the mean PAC skill of the whole reforecast period

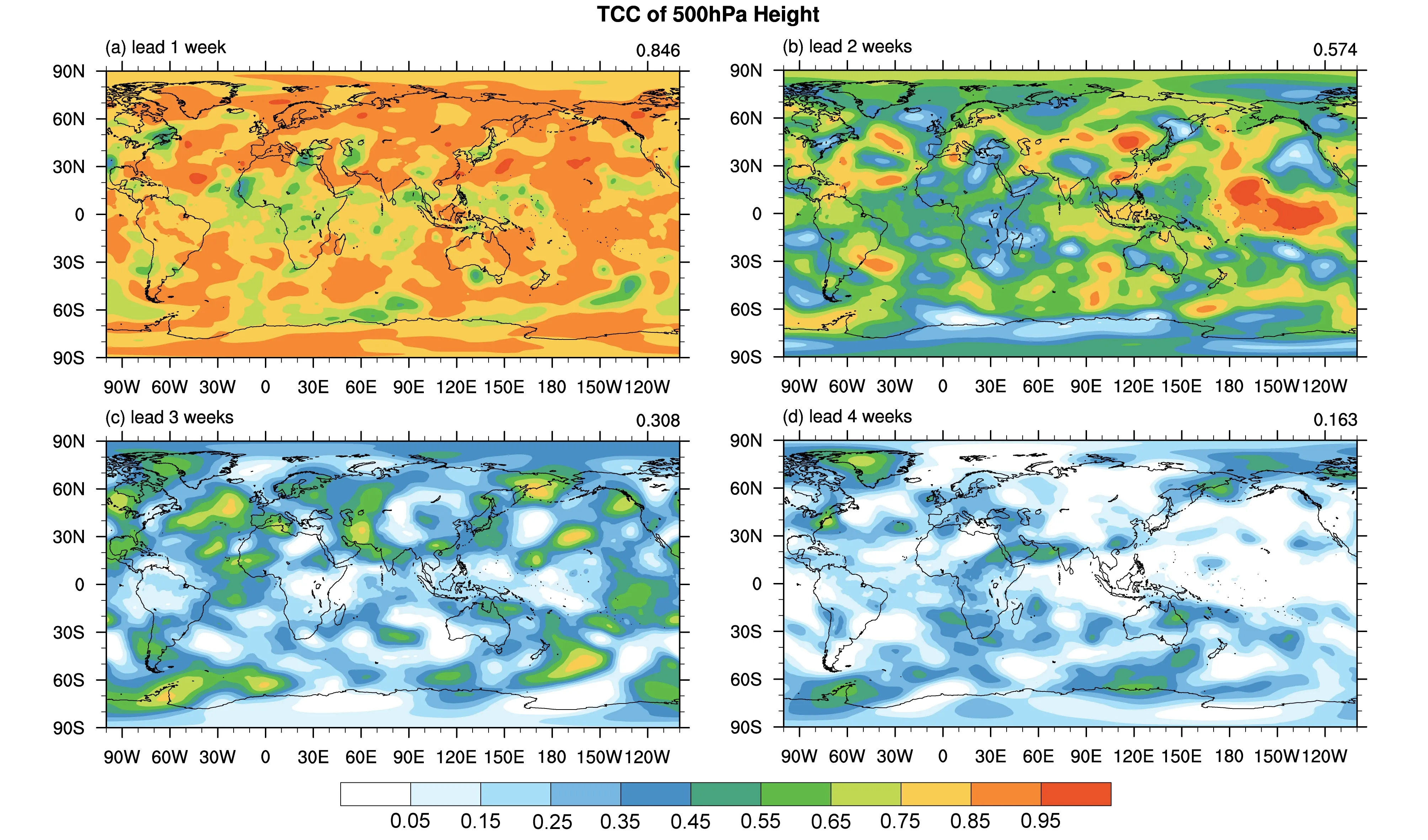
图9 GRAPES-GFS 模式对500 hPa 位势高度场超前预报（a）1 周、（b）2 周、（c）3 周和（d）4 周的时间相关系数（TCC）。其中，右标题的数字表示全球平均的TCC 技巧Fig.9 TCC of 500-hPa geopotential height forecasts during weeks 1, 2, 3 and 4 for (a) leading 1 week, (b) leading 2 weeks, (c) leading 3 weeks and(d) leading 4 weeks. The numbers in the right title indicate the mean TCC over the global areas

4.4 GRAPES-GFS 对热带MJO 的预报能力

20 世纪70 年代初，Madden 和Julian 发现季节内振荡存在于热带地区，起源于热带印度洋和西太平洋，并以热带地区对流的向东传播为主，绕全球一周，但在印度洋及西太平洋季风区表现更为明显（Zhang, 2005）。更多的研究表明，MJO 对亚洲季风活动（Zhang, 2005; Lau and Waliser, 2012）及中国东部降水有显著的影响（李崇银，2004；Zhang et al., 2009；丁一汇和梁萍，2010）。作为连接数值天气预报和季节预测的桥梁，MJO 对延伸期次季节预报有重要应用价值。因此，本研究尝试使用天气模式GRAPES-GFS 对MJO 的预报效果进行分析，以初步探讨GRAPES-GFS 的延伸期次季节预报能力。

GRAPES-GFS 模式的大气层顶层向外长波辐射OLR 预报资料：大气层顶层的upward longwave rad. flux（简称ulwrf）变量。在模式中，该变量输出的是随时间的累计积分结果。因此，逐日的长波辐射通量资料，需要次日的减去前一日的，并对24 小时做平均。具体分析为：模式输出的tn+1时刻的长波辐射通量为Itn+1，模式输出的tn时刻的长波辐射通量为Itn，记第tn+1天的平均长波辐射通量为n+1， 第tn天的平均长波辐射通量为xtn，则

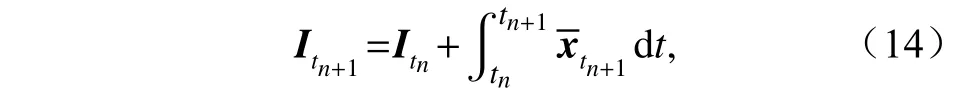
因此，

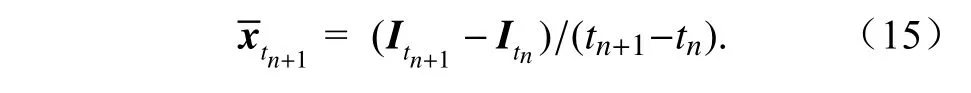
GRAPES-GFS 模式的OLR 分析场采用国家卫星气象中心提供的风云3 号卫星（FY3C）的实时OLR 场。由于FY3C 观测的OLR 资料的长度较短，因此在计算距平场时，选用的气候态为NOAA 的1981～2010 年共30 年平均的OLR。

本文采用反映热带对流和降水特征的OLR 场及对流层高、低层纬向风场异常来监测MJO 的传播和强度。另外，本研究采用Wheeler and Hendon（2004）定义的RMM1 和RMM2 指数作为MJO实时预报的监测指数。具体步骤如下：首先，对监测要素做20 天的带通滤波；一方面，去除噪音信号的干扰；另一方面，最大可能地保留预报资料的信息。其次，对近赤道平均的850 hPa 和200 hPa纬向风及OLR 做联合EOF（CEOF）分解，得到近赤道地区MJO 空间结构的前两个主模态EOF1和EOF2。然后，在MJO 的实时监测中，将实时的多变量投影于上述两个主模态，从而得到主成分RMM1、RMM2，基于RMM1、RMM2 确定的位相分布图，可给出MJO 事件空间位相的逐天演变。其中，MJO 强度由RMM1、RMM2 平方和的算术平方根确定，当其大（小）于1，即位于位相图中的圆圈外（内）时，为强（弱）MJO。

4.4.1 MJO 基本要素—风场及OLR 场的预报效果分析

时间—经度剖面可直观地展示MJO 的传播。本节基于描述MJO 传播的基本要素850 hPa 纬向风场（U850）、200 hPa 纬向风场（U200）和OLR资料，将GRAPES-GFS 分析场中描述MJO 的要素与NCEP/NCAR 再分析资料进行对比，从而对GRAPES-GFS 模式性能做初步评估。近赤道地区（15°S～15°N）850 hPa 纬向风场及200 hPa 纬向风场分别对应着低空急流和高空急流，这两个层次的风场异常，其传播特征和模态特征均与NCEP/NCAR 再分析资料一致，如图10a1、a2、b1、b2。譬如，在2019 年1 月初，低空850 hPa 的西风异常发展自赤道90°E 开始，逐渐向东传播至东太平洋，盛期时异常海面风变大变强，随后传至150°W 衰退；而到2019 年2 月份，东风异常又从赤道90°E 开始传播，进行下一个循环发展。与此同时，高空200 hPa 的西风异常在2019 年1 月份自赤道140°W 开始逐渐向东传播发展，在110°W局地变强，随后在 2019 年2 月份衰退。另外，两套分析资料都显示，纬向风的振幅在冬季（DJF）最大，夏季（JJA）最小，而且季节内振荡在印度洋和西太平洋最为明显。

图10 GRAPES-GFS（第一行）、NCEP/NCAR（第 二行）分析场中MJO 基本要素距平场在2018 年9 月至2019 年8 月在热带 地区15°S～15°N 平均的发展：（a1、a2）850 hPa 纬向风；（b1、b2）200 hPa 纬向风；（c1、c2）OLRFig.10 Composite evolution of the basic elements related to MJO averaged over 15°S–15°N as derived from GRAPES-GFS (top line) and NCEP/NCAR (bottom line) reanalysis: (a1, a2) 850-hPa zonal wind anomaly; (b1, b2) 200-hPa zonal wind anomaly; (c1, c2) the OLR anomaly

对于赤道（15°S～15°N）平均的OLR 距平场，GRAPES-GFS 在赤道印度洋和西太平洋上的信号传播特征和NCEP/NCAR 较为接近，但在赤道60°W 位置处正距平较弱，对流季节振荡变化不明显。进一步地，在对比GRAPES-GFS 与NCEP/NCAR的OLR 全球季节平均的空间分布后（图11），两套资料都显示：热带季节内振荡有明显的季节变化，冬季主要活动在赤道以北，夏季则主要活动在赤道以南。和NCEP/NCAR 相比，GRAPES-GFS 冬季偏差大于夏季，且在赤道地区正距平信号偏弱，负距平信号偏强，但可以抓住较强的对流活动信号的具体位置。GRAPES-GFS 模式分析场采用的风云3 号卫星FY3C 的实时OLR 资料，其在赤道地区具有显著的负距平，这表明，和NOAA 的1981～2010 年共30 年平均的OLR 气候态资料相比，GRAPES-GFS 模式分析场具有显著的负偏差。

图11 2019 年夏季平均与2018 年冬季平均的（a1、b1）GRAPES-GFS 分析场和（a2、b2）NCEP/NCAR 再分析资料中OLR 距平场（单位：W m−2）季节平均的空间分布Fig.11 The seasonal average of OLR anomaly (units: W m−2) from (a1, b1) GRAPES-GFS and (a2, b2) NCEP/NCAR reanalysis during the summer in 2019 and winter in 2018, respectively

低空和高空风场代表大气循环及能量传播，OLR 场可反映热带对流和降水特征。因此为评价MJO 各要素预报产品的表现随预报时间的变化趋势，我们重点分析了低空850 hPa 纬向风场、高空200 hPa 纬向风场和大气OLR 场。图12 给出了低空、高空纬向风场和大气OLR 场的距平相关系数ACC 随预报时长的变化。其中，纬向风场的参考态为GRAPES-GFS 的分析场，OLR 场的参考态为国家卫星中心提供的风云FY3C 的日平均OLR 场。随着预报时间的增加，ACC 的变化趋势逐渐趋于平稳，且预报能力逐渐降低。其中，U850 和U200 纬向风有着相似的预报技巧变化趋势，且在预报初始阶段预报技巧都较高。如果以ACC 为0.5 作为有效的预报技巧，可以发现，U850 和U200 分别在6.9 天和7.1 天之后，相关系数下降到0.5 以下，并在2 周左右下降趋势逐渐趋于平稳；OLR 的ACC 预报技巧相对比较平稳，在9.3 天之后相关系数下降到0.5 以下，随后在较长一段预报时间仍保持着一定的相关性。

图12 赤道地区（15°S～15°N）平均的MJO 基本要素距平场的距平相关系数Fig.12 Anomaly correlation coefficients by lead days for the basic elements related to MJO averaged over 15°S–15°N

4.4.2 MJO 的预报效果分析

为了考察GRAPES-GFS 模式中MJO 的预报技巧，首先利用GRAPES-GFS 的分析资料得到相应的MJO 空间分布。具体方法如下：将15°S～15°N范围内U850、U200 和OLR 资料去掉时间平均，对得到的距平场资料进行20 天的带通滤波，以除掉噪音信号的干扰；然后对经过上述处理的数据进行纬向平均，以去掉纬向变化；为保证上述3 个变量在CEOF 分析中具有相同的方差贡献，分别对上述3 个变量进行标准化处理；最后进行联合EOF分析。

分别对GRAPES-GFS 和NCEP/NCAR 资料中的U850、U200 和OLR 三个变量距平的联合场进行EOF 分析，得到2 套资料前2 个模态的空间型EOF1 和EOF2（图13）。结果表明，两套资料的两个模态空间型均近似正交，表现出MJO 纬向1波的特征，其中，U200 和U850 的反位相关系可反映出大气的斜压结构。在GRAPES-GFS 资料的EOF 第一模态（EOF1）中，纬向风场在120°E 附件发生变化，在EOF 第二模态（EOF2）中，纬向风场在60°E 和180°附件发生变化，风向的变化有利于增强大气对流。在NCEP/NCAR 资料中，EOF1 的纬向风场在90°E 附近发生变化，EOF2 的纬向风场在60°E 和150°E 附近发生变化。另外，两套资料的OLR 场发生变化的经度位置和振幅大小也存在差别。但总体上， GRAPES-GFS 模式中U850、U200 和OLR 的变化趋势与NCEP/NCAR接近，可以反映出MJO 的信号。进一步地，基于GRAPES-GFS 超前1～35 天预报时长下利用实时多变量计算得到的时间序列RMM1 和RMM2，以及利用GRAPES 的分析场（包括风场及风云3 号卫星FY3C 的实时OLR 场）计算得到的RMM1和RMM2 指数，给出了MJO 预报技巧RMM1+RMM2 的距平相关系数随预报时长的变化，见图14。在预报前15 天，相关系数迅速下降，随后趋于平稳。如果以相关系数0.5 作为有效的预报技巧，可发现，MJO 有效的预报时长为11 天左右，与一般大气模式的预报水平接近。表明，GRAPES-GFS对MJO 是有一定的预报能力的。

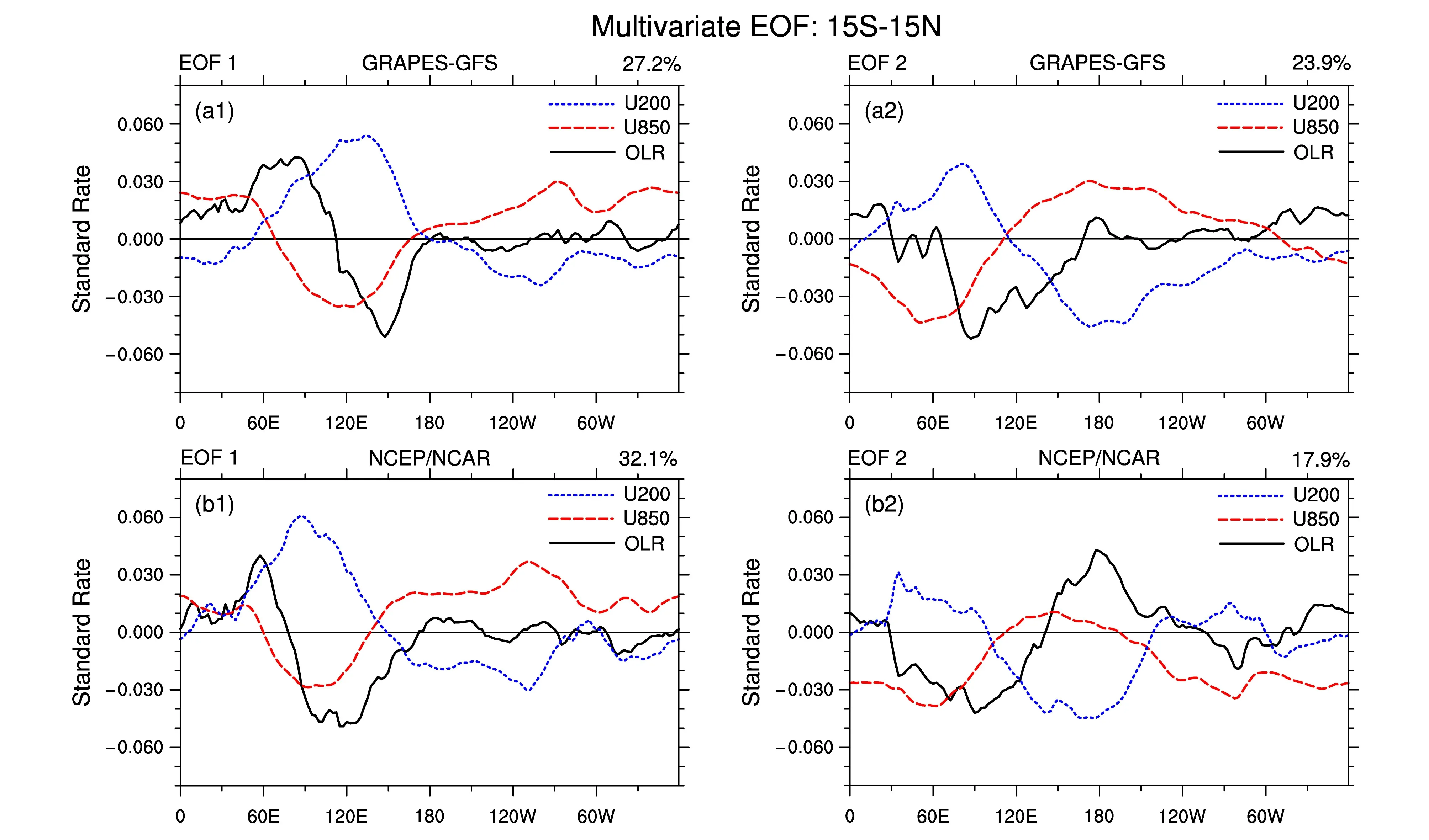
图13 由赤道（15°S～15°N）平均的 OLR 距平、U850 距平和 U200 距平的联合EOF 获得的第一、第二模态纬向结构。其中，第一行是关于GRAPES-GFS 的，第二行是关于NCEP/NCAR 的。所有变量均进行标准化和带通滤波处理Fig.13 The first mode (EOF1) and second mode (EOF2) of EOF of averaged over (15°S–15°N) OLR anomaly, U850 anomaly and U200 anomaly from GRAPES-GFS analysis data (top line) and NCEP/NCAR analysis data (bottom line). All variables are normalized and are 20-d band-pass filtered

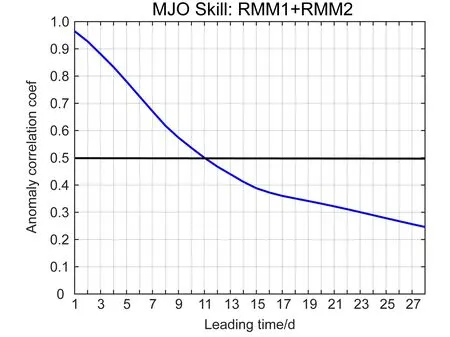
图14 2018 年9 月至2019 年8 月RMM1+RMM2 的距平相关系数Fig.14 the anomaly correlation coefficient of RMM1 plus RMM2 for the period of September in 2018 to August in 2019

以2019 年4 月15 日至6 月12 日为例，图15b反映了该个例中MJO 对流活动从印度洋（第2、3位相）开始向东传播，经海洋大陆地区（第4、5位相）到西太平洋（第6、7 位相），再经西半球和非洲西印度洋（第8 和第1 位相），并最终在西印度洋（第2 位相）消失的过程。此次传播过程为一次完整的MJO 活动周期。与澳大利亚气象局的实时RMM 产品相比，GRAPES-GFS 在超前6 天的预报上，也可以准确地刻画此次MJO 事件的东传过程，但GRAPES-GFS 模式在初始阶段具有较大的相位误差，且在MJO 的发展和衰亡阶段描述的强度偏强，在成熟阶段MJO 的强度较弱。

5 总结和讨论

本文采用GRAPES-GFS 模式1～35 天预报的历史数据，通过和其它再分析资料对比，对该系统地面要素2 m 温度和高空要素500 hPa 位势高度场的次季节预报效果进行诊断分析，给出其分析场误差和次季节预报的系统误差的空间分布，并评估了GRAPES-GFS 模式对地面和高空要素的次季节预报能力。另外，作为连接数值天气预报和季节预报的桥梁，MJO 对延伸期次季节预报有重要应用价值，因此，本文也评估了GRAPES-GFS 模式对MJO 的预报能力。结论如下：

（1）对于2 m 温度，GRAPES-GFS 模式分析场与NCEP/NCAR 及ECMWF 再分析资料相比，夏季误差比冬季误差大，且误差受海陆分布与地形分布差异影响较大，陆地比海洋区域误差更大，尤其在热力强迫作用显著的非洲干旱区，系统呈现显著的正偏差。对于500 hPa 位势高度，模式可模拟出2018 年冬季和2019 年夏季位势高度的条带状分布，但相比于NCEP/NCAR 分析资料，冬季偏差要高于夏季，高纬度地区偏差要明显高于低纬度偏差。

图15（a）2018 年11 月13 日 至2019 年1 月20 日 和（b）2019 年4 月15 日 至6 月12 日 澳 大 利 亚 气 象 局（ABOM）的 实 况、NCEP/NCAR 再分析资料以及GRAPES-GFS 超前6 天预报的MJO 空间位相传播对比Fig.15 The RMM phase space diagrams as derived from MJO products of Australian Bureau of Meteorology (ABOM), NCEP/NCAR reanalysis data and leading 6-day predictions of GRAPES-GFS, respectively, for (a) the period of November 13, 2018 to January 20, 2019 and (b) the period of April 15, 2019 to June 12, 2019

（2）关于GRAPES-GFS 模式1～35 天的2 m温度预报，在去除海洋区域的偏差后，模式次季节预报的系统性能偏差主要分布在热力强迫作用显著的高原沙漠地区，当超前更长时间的预报时，该偏差更为明显。均方根误差在超前1～3 周预报时近似于线型增长，并逐渐趋于饱和，TCC 预报技巧较高的区域在东亚及澳大利亚等地区；关于500 hPa位势高度，在超前1～3 周预报时长内，PAC 预报技巧近似于线型下降，在超前4 周预报时，预报技巧趋于稳定，综合超前1～4 周的预报，东亚中低纬度预报技巧明显高于中高纬度地区，热带地区的远低于其他地区，北半球的预报技巧高于南半球。

（3）对于描述MJO 传播的基本要素（850 hPa纬向风场和200 hPa 纬向风场），GRAPES-GFS 模式分析场描述的传播特征和模态特征均与NCEP/NCAR 再分析资料一致；另外，850 hPa 和200 hPa纬向风有着相似的ACC 预报技巧变化趋势，且在预报初始阶段，预报技巧相对较高，随后逐渐下降，并趋于平稳。对于OLR 场，和NCEP/NCAR 再分析资料相比，GRAPES-GFS 模式可抓住赤道印度洋和太平洋上较强的对流活动信号的传播，但和NCEP/NCAR 相比，GRAPES-GFS 冬季偏差要高于夏季，且在赤道地区正距平信号偏弱，负距平信号偏强，尤其在赤道60W 位置处存在明显的系统偏差。

（4）对MJO 传播的三个基本要素做CEOF 分析，结果表明，GRAPES-GFS 模式可反映出MJO纬向1 波的特征，且可呈现出大气的斜压结构，与实际信号吻合。MJO 有效的预报时长为11 天左右，与一般大气模式的预报水平接近。表明，GRAPESGFS 对MJO 是有一定的预报能力的。对于选取的两次强MJO 事件个例，与澳大利亚气象局提供的实时MJO 空间位相传播相比，GRAPES-GFS 在超前6 天的预报上，可以较准确地刻画2 次强MJO事件的传播过程，对应的MJO 对流活动中心也基本与实时RMM 指数反映的情况吻合，但GRAPESGFS 模式描述的MJO 信号，其在MJO 的发展和衰亡阶段描述的强度均偏强，对于2019 年春季的强MJO 个例，其在初始阶段具有较大的相位误差。

GRAPES-GFS 模式总体上能够描述各要素在延伸期次季节尺度的基本特征，但还存在诸多有待改进和提高之处。结合本文的分析，2 m 温度在非洲干旱区存在大的分析误差，以及在热力强迫作用显著的高原沙漠地区，存在较大的预报系统偏差。OLR 距平场在赤道地区正距平信号偏弱，负距平信号偏强，与其它再分析资料差别较大。对于强MJO 事件，和其它实时的气象产品相比，还存在较大的强度和相位误差。然而，采用不同的同化分析方法、提高地形资料分辨率和完善全球陆面同化系统，对GRAPES-GFS 预报效果的影响均较大，因此，在未来，还需要对模式中热力强迫作用显著地区的2 m 温度以及大气顶层的长波辐射资料进一步改进和完善，并对陆面同化系统加以完善，以减少模式的系统性偏差。另外，GRAPES-GFS 模式是大气环流模式，未能充分考虑海气相互作用的影响。诸多研究表明，数值模式中下垫面海温SST对MJO 可预报性有重要影响，可显著提高模式对MJO 的预报能力（Woolnough et al., 2007; Pegion and Kirtman, 2008; Zhu et al., 2017）。因此，未来我们将实时更新GRAPES 模式积分过程中的海温场，做1～35 天的预报，进一步比较分析模式对延伸期次季节预报的可预报性。进一步地，数值预报模式受初始误差、模式误差及大气混沌特性的影响，天气预报存在着较大的不确定性，而集合预报是估计这种预报不确定的重要工具之一（Lewis, 2005;Buizza et al., 2005; 麻巨慧等, 2011）。因此，在未来，我们将基于GRAPES 全球集合预报系统，从初始误差和模式误差的角度，探讨该业务系统对次季节预报的影响。