一个基于Eta 垂直坐标的新WRF 动力框架及其数值试验
程锐 宇如聪 徐幼平 刘娟 黄静
1 地理信息工程国家重点实验室,西安710054
2 中国气象局,北京 100081
3 中国科学院大气物理研究所大气科学和地球流体力学数值模拟国家重点实验室(LASG),北京 100029
1 引言
开发动力框架和设计相应的求解算法是模式发展的焦点问题之一。WRF(Weather Research and Forecasting model)动力框架考虑了更高阶数值精度和标量守恒为特性的数值算法,物理过程选项丰富、计算高效,同时具备可移植性、并行化、可扩展性;用于封装模式的软件框架考虑了多层级软件架构以及应用程序编程接口(API)设计等功能(Michalakes et al., 2001),可组装动力框架、物理过程、I/O 等模式元素。可以看出,该动力框架具备设计先进性、算法精确性和求解高效性,既能把模式元素富有逻辑、高效科学地组织起来,同时也确保了系统的可扩展、易于开发及大规模并行计算等功能,是现今利用率较高的先进模式框架。
WRF 模式在东亚地区获得了广泛应用,为中尺度天气预报机理研究和暴雨、台风等模拟预报提供了有力工具;但和其他数值模式一样,对于复杂地形下暴雨预报性能仍然不高。借鉴Eta 坐标模式对陡峭地形有效处理(Mesinger, 1984, 2004; 宇如聪 和 徐 幼 平, 2004; 普 业 等, 2008; 程 锐 等, 2018,2019),若能在WRF 模式中采用阶梯地形垂直坐标进行复杂地形表达,改善陡峭地形下气压梯度力、水平平流和扩散等过程的刻画,则既是对该模式功能的有益提升,也能够对解决复杂地形下暴雨预报问题提供一定参考。
1.1 垂直坐标设计
垂直坐标构造是数值模式的重要内容;理论上,在数值天气预报中,凡与几何高度有单调关系的任何变量都可作为垂直坐标,不同坐标变换仅仅带来方程组形式变化以及边界条件的改变。Richardson最初进行数值天气预报设计时采用了几何高度坐标,并由Kasahara and Washington(1967)实现利用高度坐标系进行数值天气预报。Eliassen(1949)提出气压作为垂直坐标的概念,并得到广泛应用;后来,为了更好处理下边界,Phillips(1957)使用了归一化坐标(σ=p/ps);再后来,由归一化坐标逐渐发展为基于高度(Gal-Chen and Somerville, 1975)和质量(Laprise, 1992)的地形追随坐标。基于Egger(1972)的地形障碍方法,曾庆存1982 年提出一种改进的Sigma 坐标(手稿;稿件题目:修改的σ 坐标),与Mesinger(1984)提出的Eta 坐标一致,都为阶梯地形坐标。现在比较流行的垂直混合坐标的概念由Sangster(1960)提出,他建议模式低层采用Sigma 坐标,高层逐渐采用气压坐标,从而在高层避免气压梯度力大量小差问题。Steppeler et al.(2002)将模式地形表示为线性连续样条函数形式,相当于倾斜阶梯地形坐标。
在选择垂直坐标时,首先要考虑是否适合处理地形。地形是大气运动重要的强迫源,既可将其看作阻滞气流的巨大障碍物,也可看作是矗立在对流层的热岛和水汽供应源(纪立人等, 2005);地形还是对流活动的触发源。中尺度数值模式的主要目的是描写大气中与灾害天气有关的强对流活动,而大陆上的对流灾害天气又往往和地形强迫作用密切相关。另外,随着模式分辨率的提高,陡峭地形坡度越来越大;比如2 km 分辨率的中尺度模式,地形坡度能达到0.3 左右,而一般的天气模式地形坡度小于0.01(胡江林和王盘兴, 2007)。因此,精确、合理的构造模式地形是数值天气预报的重要问题,尤其我国境内存在青藏高原等复杂地形,与地形相关的数值计算与处理更值得深入研究。
1.2 地形追随坐标的问题及其改进
地形追随坐标下,因坐标系非正交,所以会产生虚假曲率影响;由于坐标面不水平,水平平流和扩散处理需要额外人为控制;尤其是陡峭地形下气压梯度力的计算精度不高(Mesinger, 2004)。当然,地形追随坐标对陡峭地形处气压梯度力的求解误差可带来气象场模拟预报偏差(李兴良等, 2005;李兴良和陈德辉, 2015)。选用该垂直坐标,对背风坡气旋、冷空气阻塞等山脉下风方天气事件的模拟和预报也存在困难。
对于地形追随坐标模式,提高水平气压梯度力计算精度有多种应对方案,包括设计协调的差分格式(Corby et al., 1972;该格式在MM5 中得到应用)、反插回等压面计算(Smagorinsky et al., 1967;胡江林和王盘兴, 2007)、扣除法(曾庆存,1963,1979;钱永甫和周天军, 1995;WRF 模式中也采用了这种方法)以及上下层平均法(钱永甫等, 1978)等。另外,可将σ坐标变换为p–σ混合坐标,从而提高气象要素模拟精度。事实上,钱永甫(1985)就提出一个5 层p–σ混合坐标原始方程模式;赵鸣和方娟(1996)将其发展为9 层混合坐标模式。Steppeler et al.(2002)将模式地形表示为线性连续样条函数形式,并使用z和σ混合坐标构造LMz(z-coordinate nonhydrostatic version of the Lokal model)模式,其中动力框架在z坐标计算而物理过程在σ坐标计算。该方法是地形追随坐标和阶梯地形坐标的折衷方案,可以同时克服上述阶梯地形坐标及追随地形坐标的一些问题。WRF 模式也将混合坐标开发作为模式更新的重要内容,在其混合垂直坐标框架中,靠近地形的模式低层采用地形追随坐标,而地形之上逐渐向等压面坐标过渡松弛;这样既满足了易于地形处理的需要,同时也减小了地形对于模式高层的人为影响,从而使对流层顶的模式代表性得到增强。
上述修正主要针对动力计算层面,还可以通过减缓模式坐标面坡度,从而减小地形追随坐标计算误差的方式提高计算精度。Schär et al.(2002)提出一种新的平滑层垂直坐标(SLEVE),他们通过平滑复杂地形以上Sigma 坐标面来提高计算精度,并成功将此方法运用于COSMO(Consortium for Small-scale Modeling)模式中;后来,Zängl(2003)将该方法推广到质量追随坐标模式中。美国跨尺度预报模式(Model for Prediction Across Scales,简称MPAS)采用平滑地形追随(STF)混合坐标(Klemp, 2011),通过控制地形对坐标面的影响使得高层坐标面逐渐水平,从而使气流更趋平滑,这种调制作用在模式分辨率提高时尤显重要。相比SLEVE 方法,STF 方法对地形追随坐标面平滑更大。李超等(2019)基于GRAPES 模式对国际先进的平缓-混合坐标(Smoothed and Hybrid Terrain Following coordinate)进行了系统分析、试验,设计一种改进的余弦三角函数为基函数的平缓-混合坐标(COS 坐标),使低层坐标面垂直分布更加均匀,低层地形作用衰减的垂直变化更加均匀,减小了计算误差,提高了计算稳定性。张旭等人(2015)也利用GRAPES 区域模式,开展了Klemp(2011)和Schär et al.(2002)高度地形追随坐标理想试验研究,他们主要通过设定不同的地形衰减廓线或对坐标面地形高度进行平滑来减小小尺度地形影响。屠妮妮等(2012)、何光碧等(2015)通过滤波方案直接对模式地形进行处理,减缓地形坡度,提高模式预报性能。
为了解决追随地形坐标的非正交问题,很多人都尝试在陡峭地形之上使用数值网格生成方法设计正交的地形追随网格,从而减小模式截断误差,如Erdun(1997)提出Schwarz-Christoffel 正形变换方法并在复杂地形上产生2D 正交网格,Li et al.(2014)则设计提出3D 正交曲线地形追随坐标。
随着计算能力大幅提升,Eta 坐标模式在边界层内分层也能得到精细表述,对重力波和边界层特征的刻画能力得到提高,加之其对水平气压梯度力和平流的刻画优势,从而将Eta 坐标的应用重新提上模式发展日程。Mesinger et al.(2012)设计了一种倾斜Eta 坐标,较好清除了Gallus and Klemp(2000)发现的在原Eta 阶梯地形模式中存在的阶梯转角的虚假涡度。随后,Mesinger and Veljovic(2017)进行了该版Eta 坐标模式和Sigma 坐标模式比较试验,发现当Eta 垂直分层加密后气流分离现象得到消除。另外,Eta 模式在云物理和辐射过程以及资料同化改进后,其在降水评分上相对于Sigma 模式保持较高水平;Eta 模式优势在美国西部特别明显,对于所有降水类型Eta 模式性能更加优异,特别是较强降水。
1.3 山脉波的求解
山脉波的经典求解是给定稳定层结和平直西风情形下,分析钟形山脉激发的重力波解。实际钟形山脉可以进行阶梯地形近似,这种近似的准确性主要与地形的水平尺度以及垂直分辨率有关。1943年Lyra 推导了帽型山脉气流过山的分析解(Alaka,1960)。Gallus et al.(2000)在此基础上重新推导了旋转大气的山脉波解。
对于静力效应显著的波动,波动能量和动量垂直传播,并且波动局限于山脉上方区域,定常位相随高度向上游倾斜。此时,在转角之上产生的扰动的尺度比山脉强迫的尺度小好多,因此会产生明显的歪曲现象,也就使得每个阶梯转角之上的环流表现出强局地特征。虽然转角之上的扰动振幅与山脉宽度无关,但垂直速度随着山脉宽度增加而减小。因此,当山脉宽度增加时,这些阶梯转角扰动的相对振幅变得愈加明显。
2 Eta 坐标下WRF 动力框架
从原始方程出发,推导考虑地图投影变换和扰动变换的Eta 坐标WRF 湿动力框架如下:
(a)第一运动方程:
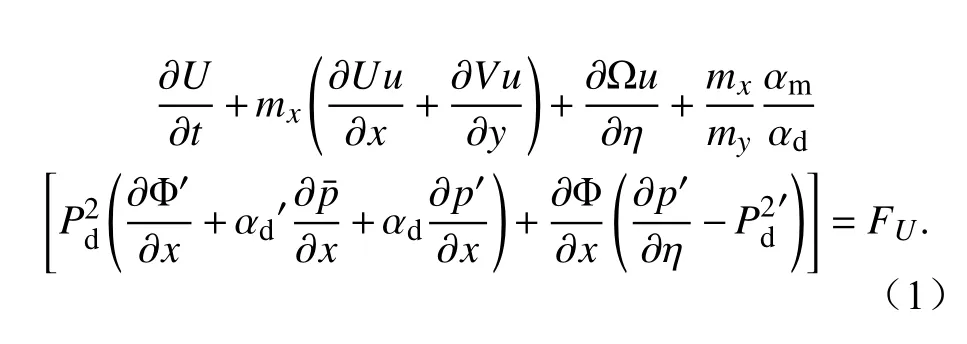
(b)第二运动方程:

(c)第三运动方程:
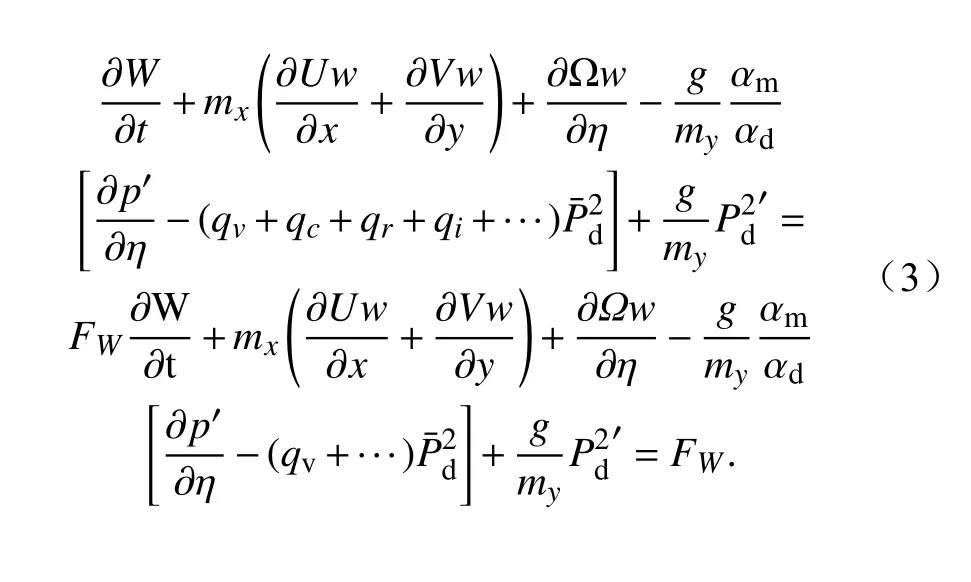
(d)连续方程:
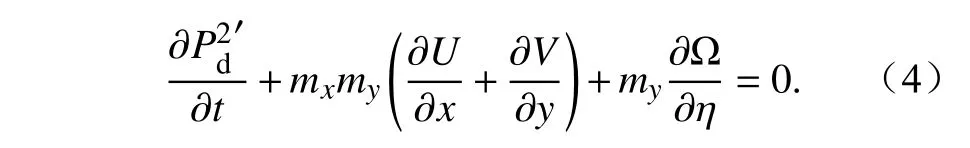
(e)热力学方程:

(f)扰动位势方程:

(g)水物质方程:
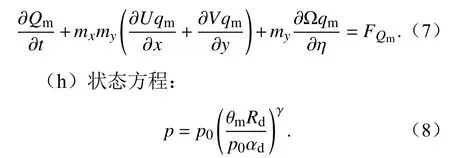
(i)静力近似方程:
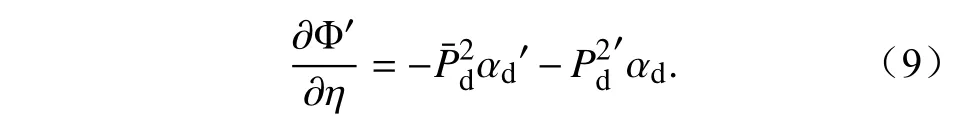
上述9 个方程共同组成了Eta 坐标下WRF 动力框架。其中,上标“ ′”表示扰动量,下标“d”、“m”分别表示干、湿过程; γ=cp/cv,cp、cv和Rd分别表示定压比热、定容比热和干空气气体常数;qv+qc+qr+qi+···表示水汽和水凝物混合比之和;(U,V,W)=(Pu,Pv,Pw),Ω=P,Θ=Pθ,Qm=Pqm,qm表 示水凝物混合比;FU、FV、FW主要为科氏力、曲率项力、混合项和物理过程转换项的贡献;FΘ、FQm主要为混合项和物理过程转换项的贡献;η表示Eta 坐标:
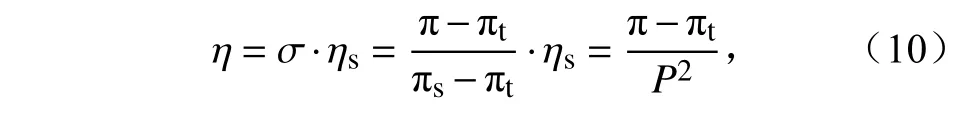
其中,
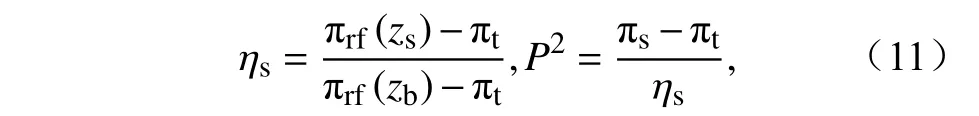
式中, π表示静力气压, πt为模式顶静力气压, πs为地面静力气压, ηs表 示地形处Eta 值; πrf为参考静力气压;zs为 地形高度,zb为 平缓地形高度, α表示大气比容,p0表示参考气压,一般取1000 hPa。
其他变量使用气象常用符号表示,不再赘述。
3 Eta 垂直坐标设计
3.1 参考状态定义
标准层结近似由曾庆存先生提出,宇如聪(1989)在中尺度模式中应用该近似方法实现静力扣除计算。本文利用标准层结大气构造阶梯地形,具体形式如下:

3.2 阶梯地形表征
3.2.1 阶梯地形2D 表征量
由于阶梯地形坐标具有准水平的性质,因此坐标面和地形存在交割关系,在不同的水平格点,大气变量在垂直方向的分布将会有三种情况:地形之下、地形表面或地形之上。在设计模式积分计算时,地形以下层次将不能参与。考虑WRF 水平网格分布为Arakawa-C 型跳点的特点,设计变量ksh(非界面层质量点紧邻地形的垂直层次编号)、ksu(纬向风点紧邻地形的垂直层次编号)和ksv(经向风点紧邻地形的垂直层次编号),对紧贴地形的Eta 坐标层次进行判断。模式垂直方向采用Lorenz 跳点形式,界面层和中间层交替分布,垂直速度和位势高度分布在界面层,其它变量分布在中间层,且从地表至模式层顶,垂直层次编号逐渐递增。

图1(a)Eta-WRF 模式的阶梯地形高度(单位:m)及阶梯坐标模式2D 表征量(b)ksh、(c)ksu、(d)ksv 随水平网格的变化Fig.1 (a) Eta-WRF Stepped mountain height (units: m) and variation of Eta model 2D-mesh indicators with horizontal grid: (b) ksh, (c) ksu, and (d)ksv
下面,我们将通过简单阶梯地形来分析ksh、ksu 和ksv 等2D 表征量与阶梯地形之间的关系(图1)。在试验中,钟形山脉实际最高高度为100 m,山脉半宽10 km,尺度系数选为zscale=0.5。从图中可以看到,在区域中心存在一个孤立地形,高约100 m;与阶梯地形对应的区域中心附近ksh、ksu 和ksv 都为2,而在其它区域为1。我们以质量点(不包括界面层变量垂直速度和位势高度)表征量ksh 为例来说明:通过阶梯地形设计,可使阶梯地形表面正好处于界面层,且紧邻阶梯地形之上的中间层和该界面层具有相同垂直层次编号;因此,“ksh=2”表示区域中心附近质量点阶梯地形所在层次为模式第2 个界面层。
3.2.2 3D 表征量
有了上述阶梯地形2D 表征量,就能够开展阶梯地形坐标下动力计算。但对于3D 格点空间的计算问题,首先进行水平网格判断,再进行垂直方向计算,会破坏数组的存取规则,影响计算效率。因此,为了方便高效开展Eta 垂直坐标模式3D 网格计算,需引入阶梯地形3D 表征量mph、mphi、mpu、mpv,分别表示模式中间层质量点所在3D 网格与阶梯地形关系、界面层质量点所在3D 网格与阶梯地形关系、纬向速度点所在3D 网格与阶梯地形关系以及经向速度点所在3D 网格与阶梯地形关系。
图2 的计算方案与图1 相同,为了更方便刻画阶梯地形3D 表征变量与Eta 垂直层次的关系,以及3D 表征量和2D 表征量表达的一致性,我们利用图中填充的阴影部分表示阶梯地形以下的网格点(其值设置为0);此处Y轴表示Eta 层次,而不是3D 表征量的具体数值。从图中可以发现,在区域中心阶梯地形处,半层质量点和速度点第2 层以下mph、mpu、mpv 为0,整层质量点第3 层以下mphi 为0。再以mph 为例进行说明:mph 在中心区域以外没有填充,表示中心区域以外没有阶梯地形存在,这和图1a 是相互对应的;在中心附近区域,因为存在孤立阶梯地形,且其位于第2 个界面层(ksh=2),因此中心区域附近第2 个界面层以下mph=0。对于界面层表征量mphi(图2b),因为中心附近区域阶梯地形位于第2 个界面层,因此第3 个界面层以上才能保证存在阶梯地形以上网格点,也就是说第3 个界面层以下mphi=0;而在中心以外区域无阶梯地形,故第2 个界面层以上就能保证存在阶梯地形以上网格点,也就是说第2 个界面层以下mphi=0。
4 山脉波试验
4.1 试验方案
原WRF(即Sigma 坐标下动力框架)山脉波试验方案作为对照试验(见表1),而将垂直坐标变换和积分时间延长作为比对试验(具体方案见表2)。通过数值试验,一方面检验更新的模式动力框架的正确性和有效性;另一方面通过对比试验考查垂直坐标选择对地形波模拟的影响。我们假定山脉地形最高为100 m,钟形山脉最高处位于区域中心,山脉半宽为10 个格距(20 km,图略),Brunt-Vaisala 频率设为10−2s−1。当前,大气背景场设置为稳定层结干大气,水平平直西风10 m s−1。数值模式选用2D 模型,模式区域水平延展202 个格点,水平分辨率为2 km,垂直方向指数拉伸分80 层,时间步长20 s,模拟时长36000 s。X方向为辐射开边界,Y方向为周期边界,Z方向刚体边界条件。水平平流采用5 阶方案计算,垂直平流采用3 阶方案计算。当前试验不考虑任何物理过程。不难看出,本方案模拟对象为典型静力特性的山脉波动,对这类波动的数值模拟也是Eta 坐标模式的难点问题之一。
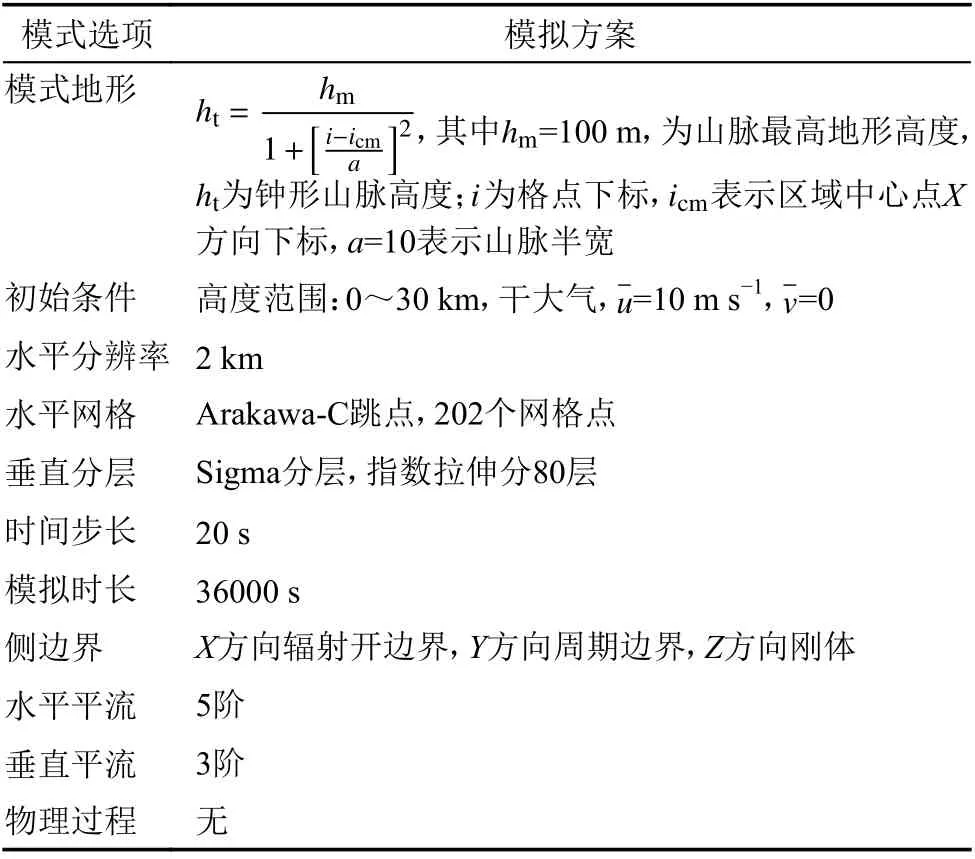
表1 原WRF 模式(Sigma 坐标)山脉波试验方案(对照试验)Table1 Original WRF (Sigma coordinates) configuration for mountain wave simulation (control experiment)

表2 Eta 坐标对比试验方案Table2 Configuration for comparative experiments with Eta coordinates
4.2 对照试验结果分析
图3 给出Sigma 坐标下WRF 动力框架对山脉波的模拟(对照试验EXP01)。从图1 可以发现,积分36000 s 时,由于钟形山脉的动力强迫,出现了明显的地形驻波特征。从温度扰动可以发现,在钟形山脉山脊靠近背风坡一侧从低层到高层存在3个大值中心(最大约0.45 K,位于模式第10 层左右),强度随高度减弱。气压扰动呈现高层弱而低层强、迎风坡弱而背风坡强的形势,最强扰动中心在背风坡靠近山脊附近,并位于模式底层,强度约−12 Pa。垂直速度分布和扰动位温相似,在山脊靠近背风坡一层从低层至高层存在交错分布的上升、下沉运动带,最大强度可达到0.04 m s−1,中心强度随高度逐渐减弱。因此,从垂直速度和扰动位温分布可以发现存在明显静力地形波动特点,波动垂直传播,且主要分布于山脊上方区域,位相随高度向上游倾斜。需要说明的是,当参考高度选为100 m时,Eta 坐标完全退化为Sigma 坐标(见方案EXP01_),与EXP01 具有相同的模拟图像(图略);伴随参考高度逐渐减小,垂直坐标变换为Sigma-Eta 混合坐标,与EXP01 模拟差异逐渐显现;当参考高度为0 时,垂直坐标为纯Eta 坐标,此时差异更加显著(具体结果见4.3 节)。
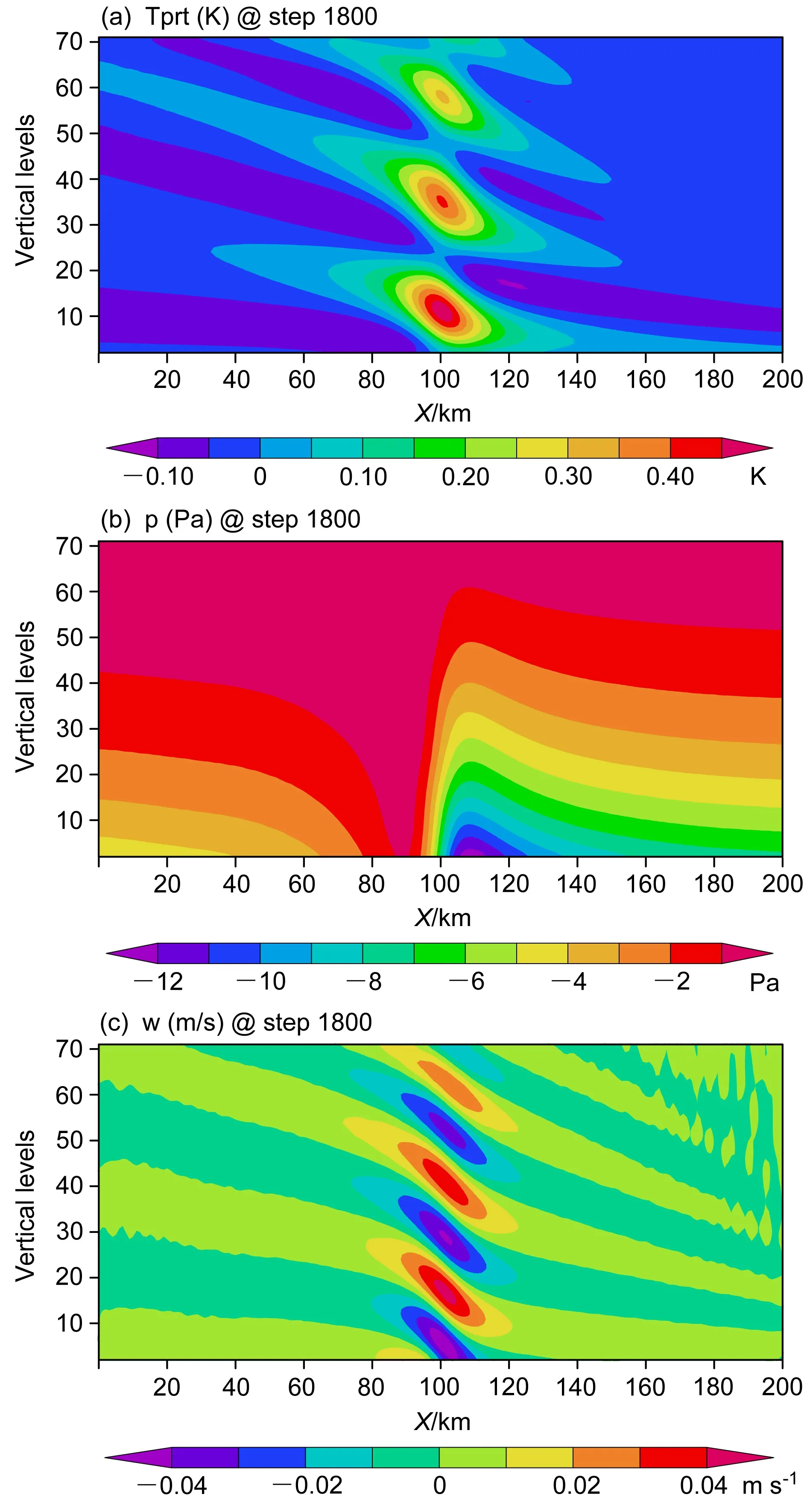
图3 EXP01 试 验 山 脉 背 风 波 动 结 构:(a)扰 动 位 温(单 位:K);(b)扰动气压(单位:Pa);(c)垂直速度(单位:m s−1)Fig.3 Structure of the mountain lee wave from experiment EXP01:(a) Potential temperature anomaly (units: K), (b) pressure anomaly(units: Pa), and (c) vertical velocity (units: m s−1)
4.3 对比试验结果分析
4.3.1 Eta 坐标(参考高度50 m)
如果将参考高度下调到50 m(如图4 所示),此时垂直速度和位温扰动呈现明显的双中心结构,中心强度明显下降(约为EXP01 的一半);气压扰动中心强度亦有减小。因此,当参考高度调整为50 m(钟型山脉最大高度的一半)时,模拟形态保持了向上游倾斜的山脉波动分布特征,但波动强度减弱,双中心结构明显。
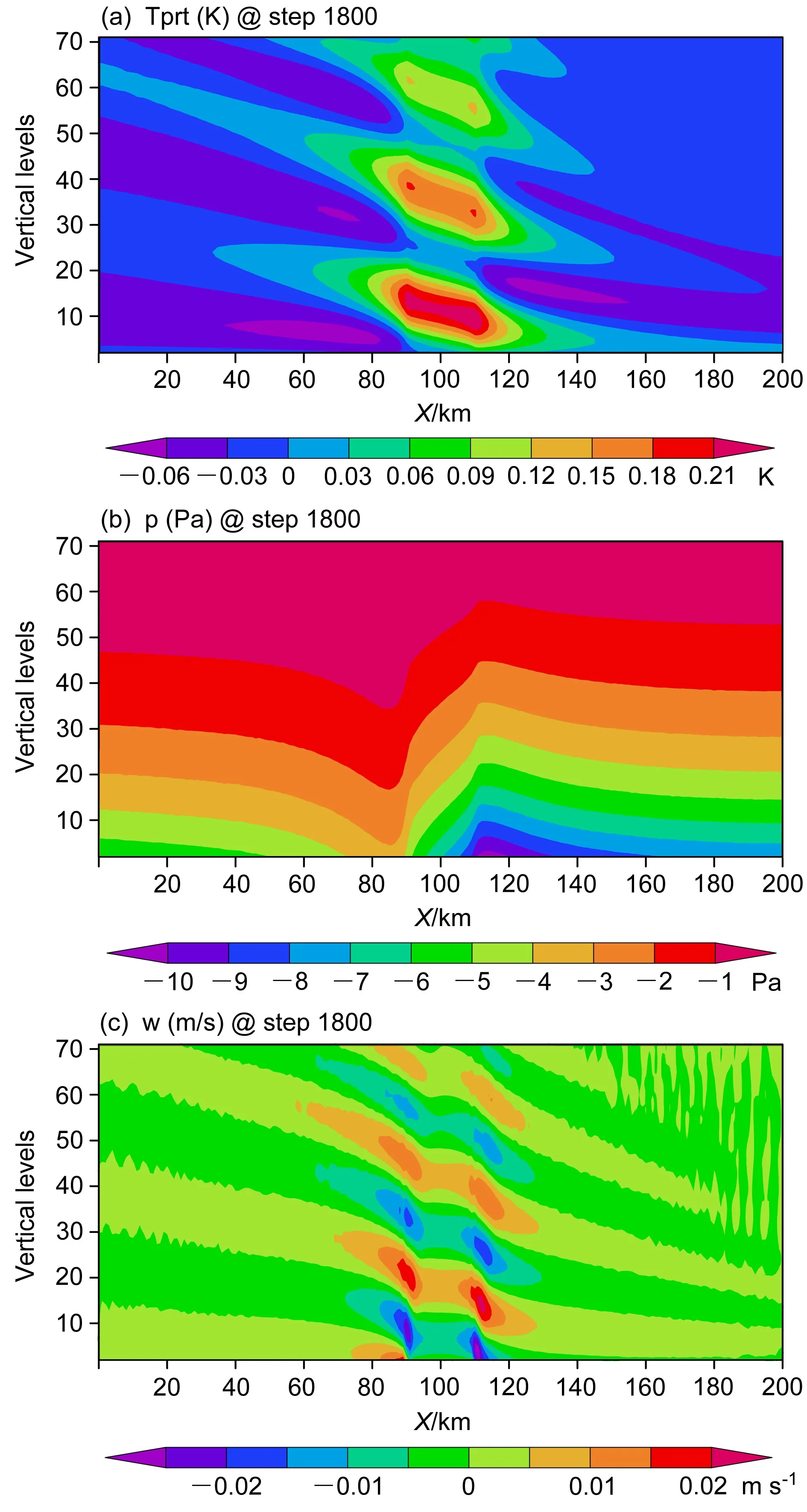
图4 如图3,但为EXP02 试验Fig.4 Same as Fig.3 but for EXP02
4.3.2 Eta 坐标(参考高度0)
如果取参考高度为0,则完全转变为Eta 坐标。图5 给出模拟结果,可以发现模拟图像发生很大变化,基本没有刻画出山脉波垂直传播、位相向上游倾斜等特征。其中,扰动气压由负转正,强度减弱;垂直速度和扰动位温强度非常弱,比对照试验减小约2~3 个数量级;另外,迎风坡主要表现为弱上升气流,背风坡主要体现为弱下沉气流。因此,Eta 垂直坐标动力框架在当前模拟方案条件下,无法正确模拟静力特性山脉波动。
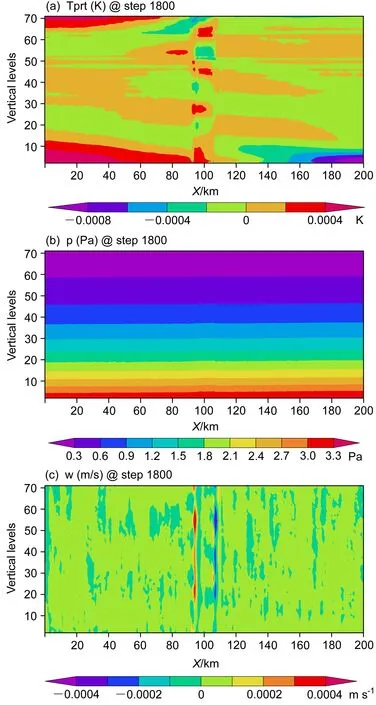
图5 如图3,但为EXP03 试验Fig.5 Same as Fig.3 but from EXP03
4.3.3 Eta 坐标(参考高度0,垂直分辨率提高)
从以上数值试验分析可以发现,Sigma 坐标和Eta 坐标模式采用完全一致的数值计算方案,但对山脉波的模拟却有很大差别:前者较好地刻画了山脉波特征,而后者几乎没有模拟能力。本节将尝试通过提高垂直分辨率来改进Eta 坐标WRF 新框架对山脉波的模拟性能。当把垂直分层从80 层提高到400 层时(图6),山脉波动特征出现,重力波垂直上传的特点比较明显,位相向上游倾斜也得到体现。不足之处在于波动垂直向上衰减更快,扰动强度虽比EXP03 强,但比起对照试验(EXP01)仍显著偏弱。

图6 如图3,但为EXP04 试验Fig.6 Same as Fig.3 but for EXP04
若将垂直分层继续提高到600 层(图略),此时山脉波模态虽仍可显现,但是波动分布较为零散,系统性不强。因此,当使用阶梯地形动力框架模拟山脉重力波时,提高垂直分辨率可以提升模拟性能,但也不是垂直分辨率越高越好。
4.3.4 Eta 坐标(参考高度0,模拟时长加大)
我们还发现,在垂直分辨率较低时(如80 层),经过长时间积分调整,也能逐渐形成山脉波。从图7 可以看出,该方案模拟出了地形波动的垂直传播及位相随高度向上游倾斜的特征,具有典型静力山脉波特征。进一步分析发现,80 层垂直分层情形下出现典型山脉波模态的时间约为220000 s,是相同垂直分辨率Sigma 动力框架模拟生成山脉波模态所需时间的6~7 倍。因此,对于Eta 坐标动力框架而言,比起相同垂直分辨率的Sigma 动力框架需要更长时间进行波动调整,才能在地形强迫下生成静力山脉波。

图7 如图3,但为EXP05 结果Fig.7 Same as Fig.3 but for EXP05
5 实例试验
5.1 北美大陆西风槽的模拟
5.1.1 试验方案
本节将利用Eta 坐标WRF 新动力框架对北美大陆西风槽演变进行模拟,并和原Sigma 坐标框架模拟结果展开对比。表3 给出北美大陆西风槽演变模拟试验方案。当前,模式分辨率取为30 km,时步180 s,积分24h;模式东西、南北和垂直方向分别为74、61 和28 个格点(对应的地理空间范围,水平方向:25.5°N~43.2°N,86.4°W~108°W;垂直方向:0~19 km),侧边界选为时变边界,垂直方向刚壁;不考虑任何物理过程。
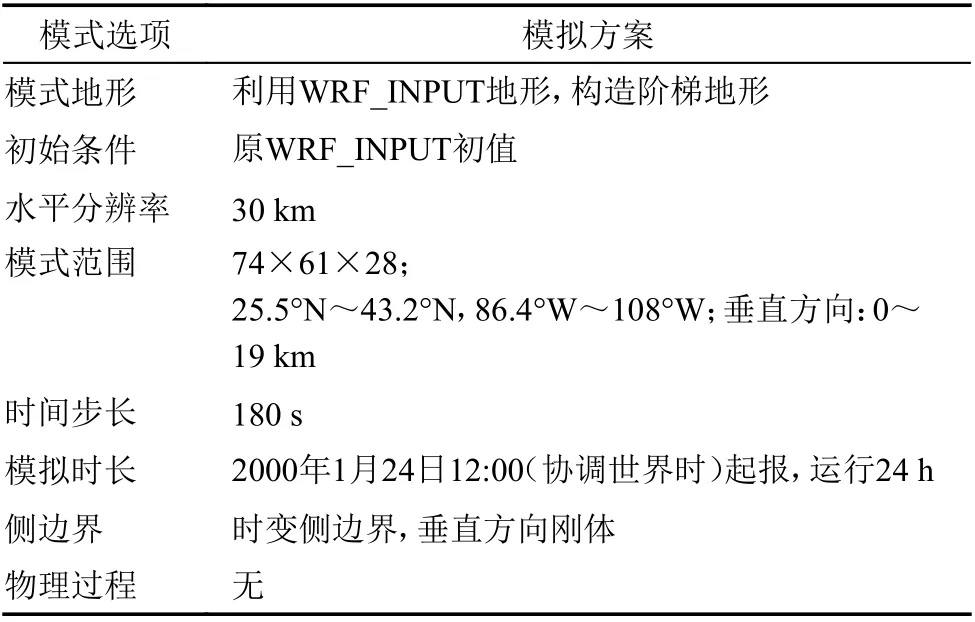
表3 北美大陆西风槽演变模拟试验方案Table3 Numerical experiment scheme for simulation on the evolution of the westerly trough in the North American continent
首先分析Eta 和Sigma 两个动力框架生成的模式地形之异同。图8 给出原WRF 模式地形和我们构造的阶梯地形分布。可以看出,新构造的阶梯地形与原Sigma 坐标下追随地形具有较好一致,如100 m 平缓地形范围及500 m 以上较陡地形分布等。从地形高度量值看,新构造阶梯地形与原WRF 地形之差在−40 m 和160 m 之间,100 m 以上地形高度差主要分布在500 m 以上较陡地形区域。这种差别可能来自于阶梯地形构造时标准大气状态的选择、Eta 垂直分层以及模式水平分辨率等因素的影响。
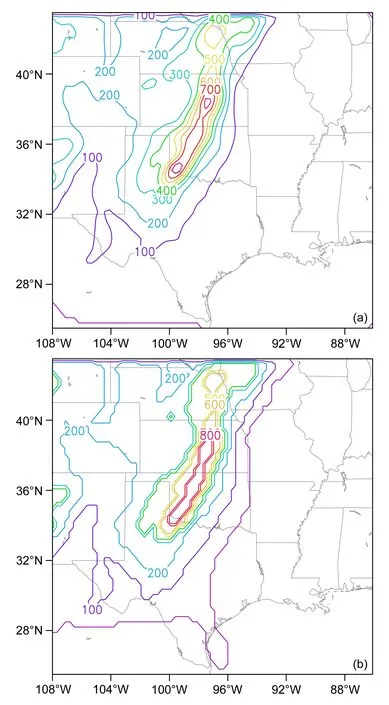
图8(a)原Sigma 坐标下和(b)Eta 坐标下WRF 模式地形高度(单位:m)分布Fig.8 Distributions of WRF model terrain height (units: m) under (a)original Sigma coordinate core and (b) Eta coordinate core
从风场的纬向—高度剖面(图9)可以发现,Eta 和Sigma 模式模拟的风场分布都是低层弱而高层强,槽区小而槽前、槽后大,且槽后更大;但Eta 坐标新框架模拟的槽前高空风速偏弱。图10给出两垂直坐标框架下模拟24 h 的500 hPa 风场分布。可以发现,选用Eta 和Sigma 垂直坐标模拟出一致的流场形势,如显著的气旋性流场分布;主要差别在Sigma 坐标模式在(36°N,94°W)附近模拟出局地中尺度气旋性涡旋,但Eta 坐标模式模拟出一致的偏南气流分布。
5.2 中国大陆槽脊系统的模拟
5.2.1 试验方案

图9(a)Eta 坐标新框架和(b)Sigma 坐标原框架模拟12 h 过32°N 的水平风速纬向—垂直剖面(单位:m s−1)Fig.9 The 12 h-simulated horizontal wind velocity across 32°N(units: m s−1): (a) Eta coordinate core; (b) original Sigma coordinate core
最后,我们来分析Eta 坐标新框架对中国大陆低槽和副高系统的模拟情况。通过该方案,主要分析新框架对我国重要天气系统的模拟性能。2012年7 月21 日03:00(协调世界时,下同)至22 日08:00,受贝加尔湖高空冷涡和西太平洋副热带高压共同影响,华北地区出现了一次大范围强降水天气过程。本节主要关注相关形势场的模拟情况。表4 给出模拟试验方案。可以看出,模拟方案与上节相同,不同之处主要体现在模式水平范围,本方案涵盖(15°N~44.7°N,109°E~144.7°E)的水平区域;另外,试验从2012 年7 月21 日00:00 起报,运行12 h。

表4 中国大陆槽脊系统模拟试验方案Table4 Numerical experiment scheme for simulation on continental weather systems in China
5.2.2 试验结果分析
图11 给出Eta 坐标新框架对中国大陆低槽及副高系统的模拟结果,并和分析场进行比较。从700 hPa 风场分布可以看出,模拟和分析风场分布较为一致,在副高控制区域,模拟形势以西南风为主,而分析则以南风为主。
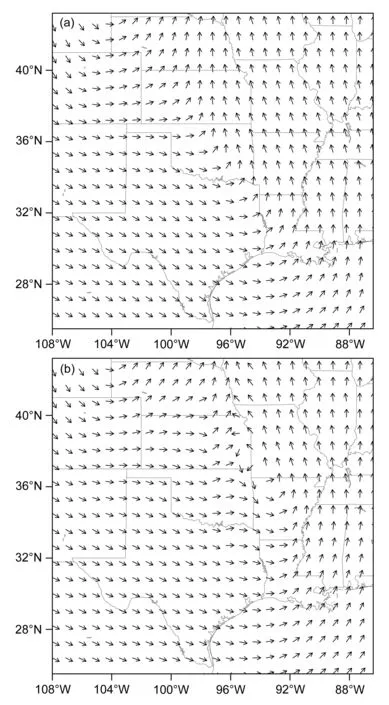
图10(a)Eta 坐标新框架和(b)Sigma 坐标原框架模拟的北美大陆24 h 500 hPa 水平风场(单位:m s−1)Fig.10 The 24-h simulated horizontal wind at 500 hPa (units: m s−1)in the North American continent: (a) Eta coordinate core; (b) original Sigma coordinate core

图 11(a)Eta 坐标新框架模拟的中国大陆6 h 700 hPa 风场分布和(b)FNL 分析场风场分布对比,单位:m s−1Fig. 11 Distributions of 6-h simulated wind at 700 hPa in the Chinese continent (units: m s−1) from (a) Eta coordinate core simulation and (b)FNL analysis
6 总结与结论
本文的主要工作是通过在WRF 模式中引入阶梯地形坐标,构造适用于复杂地形的高精度新动力框架;通过模式气柱质量变换方法,巧妙实现了Sigma 坐标和Eta 坐标下控制方程形式的完全一致,从而使Eta 坐标WRF 新动力框架计算更加便利、高效。
Eta 坐标下WRF 动力框架搭建完成后,设计理想和实例试验对新框架进行检验。主要结论如下:
(1)从动力框架形式来看,Eta 垂直坐标和Sigma 垂直坐标下WRF 的差别主要体现在模式顶与参考面之间气柱的质量定义,前者为P2=(πs−πt)/ηs, 后者为 µ=πs−πt。通过该质量变换设计,使得两个动力框架形式完全一致,从而使程序实现变得简单。
(2)引入AREM 参考大气状态用于构造WRF新动力框架阶梯地形,虽然该大气状态仍有改进空间,但其主要用于计算地表Eta( ηs)的初估值,对阶梯地形设计和模式积分计算影响不大。此外,通过设计阶梯地形2D 和3D 网格表征量使模式循环迭代与高阶差分计算过程更加简洁、高效。
(3)理想和实例试验表明,Eta 坐标WRF 动力框架运行稳定、计算合理。阶梯地形坐标动力框架可对静力地形波进行有效刻画,但前提是提高垂直分辨率或延长模拟时间。再考虑阶梯地形先判断再计算的额外时耗,相比Sigma 坐标动力框架,新框架计算花费更大。
本文主要围绕Eta 垂直坐标WRF 动力框架设计、实现及其验证展开,数值试验尤其是实例试验分析仍显初步,Eta 和Sigma 垂直坐标的差异及其原因有待今后深入分析讨论。另外,模式现有初始化仅由插值实现,物理过程参数化也未接入框架,也不利于实例试验开展。

