基于流固耦合的深基坑变形与受力分析

赵延林, 李 明, 侯月文

(黑龙江科技大学 建筑工程学院, 哈尔滨 150022)

0 引 言

深基坑工程施工通常伴随着工程降水。基坑降水会改变基坑内外地下水的渗流场与土体的应力场,引起基坑内外土体位移场的变化,最终导致基坑支护结构与周边环境产生变形。

针对工程降水对深基坑变形的影响问题,一些学者开展了一些相关的研究工作。施成华等[1]采用随机介质理论、渗流理论和土体固结压密理论,分析了基坑开挖及降水所引起的地表沉降,得出基坑降水引起的地表下沉不容忽视。董建军等[2]运用软件FLAC3D对一邻近河流的基坑工程进行模拟,得出在水位突变的情形下,基坑变形会发生显著的变化。陆建生[3]应用Modflow模拟分析悬挂式帷幕基坑,得出渗透各向异性系数越小,坑内抽水对坑外水位下降的影响越小,同时坑外回灌对坑内水位上抬的影响也越小。周勇等[4]研究了基坑开挖降水对工程周边地下管线的位移,得出了受影响变形规律。周连伟[5]通过有限元软件MIDAS GTS,在完全流固耦合的情况下,分析了降水对基坑锚杆轴力的影响。袁斌等[6]运用FLAC3D分析了某一地铁车站深基坑,得出随着止水帷幕深度的增加,坑内降水对周边的影响逐渐减小,在超过一定的值后,减小的效果不再明显。郑启宇等[7]采用软件FLAC3D对一实际工程进行模拟,得出在含承压水的基坑工程中,降水会显著改变基坑周边地表沉降。汪鹏程等[8]运用软件FLAC3D对比分析了考虑渗流效应与不考虑渗流效应两模型的差异,说明了渗流作用对模拟精度的重要性。

笔者结合实际工程,运用有限元软件MIDAS GTS NX,基于流固耦合模型与三维固结理论,分析场地地下水初始水头、降水井与地连墙深度比对深基坑变形与受力的影响,为深基坑工程的设计与施工提供理论依据。

1 工程背景

1.1 工程概况

本工程为江苏省苏州市某工业区的一个地下车站深基坑工程。基坑沿东西向布置,总长度为1 750 m,宽度为18.9 m,开挖深度为17.4 m。工程位于主要交通干道与两高架桥交叉口的中间,周边环境相对复杂,对基坑变形控制要求较为严格。

1.2 工程地质与水文地质条件

根据场地工程地质勘察报告,本工程场地土层信息见表1。地下水主要分为3类：

表1 场地土层信息

(1)潜水，主要存在于上部填土和黏性土层中,水位埋深约为1.80～3.90 m,稳定水位埋深为1.60～2.50 m。

(2)微承压水，主要存在于粉土层中,赋水性中等,最高微承压水头标高为1.74 m。

(3)承压水，主要存在于深部的粉土层中,赋水性中等,稳定水头约为1.0 m,且具有较好的封闭条件。

1.3 基坑支护方案

基坑支护方案为地连墙+四道内支撑。地连墙厚度为0.8 m,顶部设有冠梁,冠梁的截面尺寸为1.0 m×1.0 m。第1道内支撑为钢筋混凝土支撑,位于基坑顶面,截面尺寸为0.8 m×0.9 m,水平间距为6 m。其余内支撑均为钢支撑,分别距离基坑顶面5.0、8.5、11.0 m,施加的预加轴力分别为300、500、450 kN,钢支撑直径609 mm,管壁厚度16 mm,水平间距为3 m。冠梁与地连墙采用C35混凝土,钢筋混凝土内支撑采用C30混凝土,钢支撑采用Q235钢。

1.4 降水方案

基坑采用管井降水,共设立30口降水井,沿基坑内部边缘均匀分布。井深为36 m,井直径为600 mm,井间距4 m。单井出水量为160 m3/d,共降水约20 d。

1.5 土方开挖方案

土体开挖共分为5步：第1步开挖至地表下1.4 m,施工冠梁及第1道内支撑；第2步开挖至地表下7.0 m,施工第2道内支撑；第3步开挖至地表下11.0 m,施工第3道内支撑；第4步开挖至地表下14.5 m,施工第4道内支撑；第5步开挖至地表下17.4 m,开挖结束。

2 有限元模型

2.1 模型尺寸与网格划分

运用有限元软件MIDAS GTS NX建立基坑的三维计算模型,如图1所示。选择基坑工程的标准段,据以往的建模经验[9-10],将模型的尺寸定为24 m×159 m×70 m。为了能够在突出所研究问题的同时兼顾模型的计算效率,将基坑部分的网格尺寸定为2 m,外地层部分的网格尺寸定为5 m。其中,土体采用三维网格模拟,地连墙采用二维网格模拟,内支撑采用一维网格模拟。

图1 有限元计算模型Fig. 1 Finite element calculation model

2.2 单元模型与边界条件

合并参数相近的相邻土层,以简化建模过程,提高计算效率。土体采用实体单元,本构模型选择修正的摩尔库伦模型,地连墙采用板单元,内支撑采用梁单元。计算类型选择应力-渗流-边坡(渗流场与应力场单向耦合),计算理论为弹塑性计算理论。

定义模型上表面为自由边界,其余各表面采用自动约束。利用软件中的界面功能在基坑两侧生成止水帷幕,如图2所示。基于研究内容的不同,分别采用定义网格节点水头的方法与定义网格节点水头函数的方法进行模拟深基坑降水。

图2 止水帷幕及刚性连接网格Fig. 2 Waterproof curtain and rigid connection grid

2.3 模型参数

土体模型的各项参数见表1,支护体系的各项参数与支护方案见表2。

表2 围护结构参数

2.4 模拟方案

2.4.1 场地地下水初始水头

为研究场地地下水初始水头对深基坑受力与变形的影响，建立4个用于对比的模型。各模型的场地初始水头分别为2.0、5.0、8.5和11.0 m,采用定义网格节点水头的方法模拟基坑降水。预先在基坑开挖面下0.5m处生成平截面，捕捉该截面上的所有节点，定义工程降水后的水头高度。通过钝化原水头高度，激活后定义平截面水头高度来模拟基坑降水的效果。

2.4.2 降水井与地连墙深度比

为研究降水井与地连墙深度比的变化对深基坑受力与变形的影响，建立了5个用于对比的模型。各模型降水井与地连墙的深度比分别为27/31、29/31、31/31、33/31、35/31。为使各模型坑内部的降水情况完全相同,采用定义节点水头函数的方法模拟基坑降水。

3 模拟分析结果

3.1 场地地下水初始水头的影响

3.1.1 坑外地表沉降

基坑周边地表整体沉降变形曲线如图3所示。由图3可知,在地下水初始水头不同的条件下,基坑周边地表整体沉降sd曲线的分布形式基本相同,即：随着与基坑边缘距离l的不断增加,周边地表沉降均呈现出先增大后减小的变化规律；最大沉降点位于距基坑边缘12～16 m范围内,且随着地下水初始水头的降低,最大沉降点略向远离基坑方向移动；在距基坑边缘0～23 m范围内,地下水初始水头变化对地表沉降影响较为明显。

图3 地表沉降变形Fig. 3 Ground surface settlement deformation

地下水初始水头ha对基坑周边地表最大沉降位移sdmax的影响情况如图4所示。由图4可知,基坑周边地表最大沉降位移随地下水初始水头的降低而减小。当地下水初始水头由2.0 m降低到5.0 m时,地表最大沉降位移由20.5 mm减小到13.9 mm,位移减小42%;当初始水头由5.0 m降低到8.5、11.0 m时,地表最大沉降位移随地下水初始水头基本成线性变化,最大沉降位移由13.9 mm减小到13.3 和12.3 mm,位移分别减小5.0%和7.4%。由此可见,地下水初始水头在2.0～5.0 m范围内变化时,坑外地表沉降位移受影响较大。

图4 地表最大沉降位移Fig. 4 Maximum ground surface settlement deformation

3.1.2 地连墙水平位移

地连墙整体水平变形曲线如图5所示。由图5可知,在地下水初始水头不同条件下,地连墙整体水平变形sh曲线的分布规律基本相同,即“两头小,中部大”的分布形式。最大墙身水平位移出现在距地表11～15 m范围内,且随着地下水初始水头的降低,最大墙身水平位移点略有波动。顶部墙身(距地表4 m范围内)水平位移受初始水头影响较小,中部墙身(距地表7～23 m范围内)水平位移受初始水头影响较大。

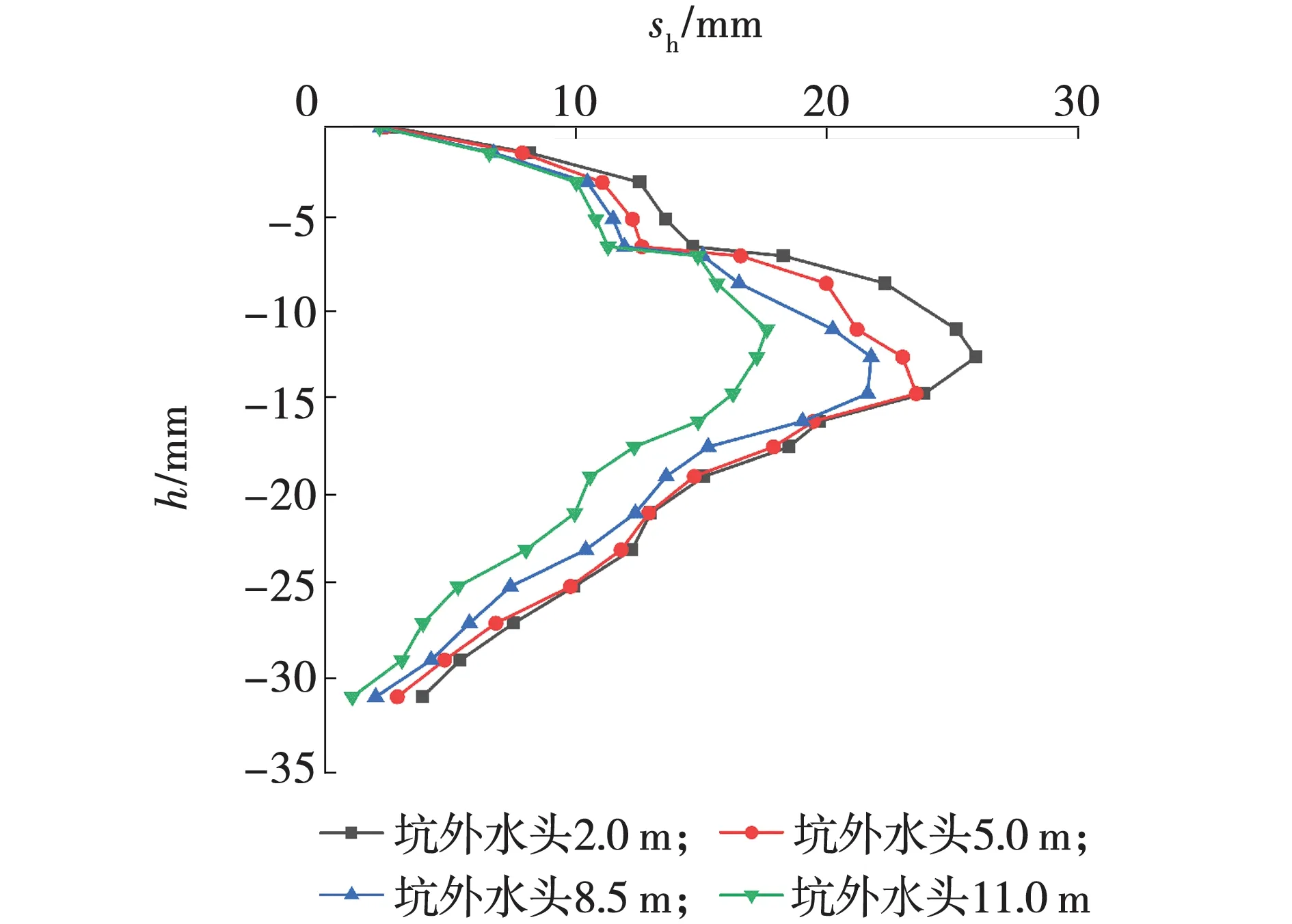
图5 地连墙水平变形Fig. 5 Horizontal deformation of diaphragm wall

墙身最大水平位移随地下水初始水头的变化曲线如图6所示。由图6可知,墙身最大水平位移随地下水初始水头的降低而减小。当地下水初始水头由2 m降低到5.0 、8.5 m时,墙身最大水平位移shmax随初始水头基本成线性变化,最大水平位移由25.9 mm减小到23.8、21.8 mm,位移分别减小8.1%和8.4%;当初始水头由8.5 m降低到11.0 m时,墙身最大水平位移由21.8 mm减小到17.5 mm,位移减小20%。由此可见,地下水初始水头在8.5～11.0 m范围内变化时,墙身水平位移受影响较大。

图6 地连墙最大水平位移 Fig. 6 Maximum horizontal displacement of diaphragm wall

3.1.3 坑底隆起位移

坑底整体隆起变形如图7所示。由图7可知,在地下水初始水头不同条件下,坑底隆起变形sl的整体分布规律基本相同,即“两边大,中间小”的塑性变形分布规律。最大隆起变形出现在靠近地连墙位置lj,坑底中部的隆起变形略小于最大隆起变形,且随着初始水头的降低,这种差异也在逐渐减小。

图7 坑底隆起变形Fig. 7 Heave displacement of pit bottom

地下水初始水头变化对坑底最大隆起位移slmax的影响情况如图8所示。由图8可知,当地下水初始水头由2.0 m降低到5.0、11.0 m时,坑底最大隆起位移随初始水头的降低成线性增加,最大隆起位移由54.6 mm增加到60.1和66.5 mm,位移分别增加10%、11%;当初始水头由8.5 m降低到11.0 m时,坑底最大隆起位移基本没有变化。由此可知,地下水初始水头变化对坑底隆起变形的影响较小。

图8 坑底最大隆起位移Fig. 8 Maximum heave displacement of pit bottom

3.1.4 地连墙弯矩

地连墙弯矩图如图9所示。由图9可知,当地下水初始水头为2.0、5.0 m时,整个墙身弯矩M均为正值,最大弯矩均位于距地表11 m处,大小分别为251、188 kN·m;当地下水初始水头为8.5、11.0 m时,墙身弯矩出现负值区域,最大负弯矩值位于距地表7 m处,大小为70 kN·m,最大正弯矩仍位于距地表11 m处,大小为87 kN·m；距地表2～13 m范围内的墙身弯矩受地下水初始水头的影响较大。

图9 地连墙弯矩Fig. 9 Bending moment of diaphragm wall

在距地表7 m处墙身附近,初始水头8.5 m相对于初始水头5.0 m,墙身弯矩发生了符号变化。这是因为：初始水头5.0 m时,地连墙上部(距地表5.0～8.5 m范围内)作用有水压力与渗流压力;初始水头8.5 m时,这部分水压力与渗流压力是不存在的,地连墙上荷载的变化导致了该部分墙身弯矩的符号变化。

距地表11.0 m处墙身弯矩随地下水初始水头的变化曲线如图10所示。由图10可知,墙身弯矩随地下水初始水头的降低而接近线性减小。当地下水初始水头由2.0 m降低到11.0 m时,墙身弯矩由251 kN·m减小到21 kN·m,减小92%。由此可见,地下水初始水头的变化对墙身弯矩影响很大。

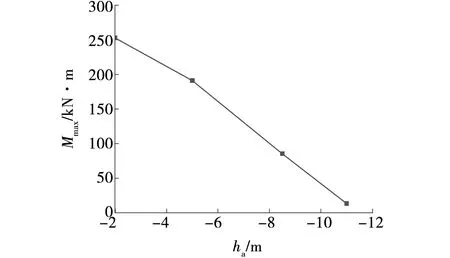
图10 距地表11.0 m处墙身的弯矩Fig. 10 Bending moment of wall at 11.0 m from surface

3.2 降水井与地连墙深度比的影响

3.2.1 坑外地表沉降

基坑周边地表整体沉降变形sd如图11所示。降水井与地连墙深度比η变化对基坑周边地表最大沉降位移sdmax的影响如图12所示。

图11 地表沉降变形对比 Fig. 11 Comparison of ground surface settlement deformation

由图11可知,在降水井与地连墙深度比不同的条件下,基坑周边地表整体沉降趋势基本相同,即随着与基坑边缘距离l的不断增加,周边地表沉降值均呈现出先增大后减小的变化特点，最大沉降点位于距基坑边缘14 m处，在距基坑边缘0～20 m范围内,降水井与地连墙深度比变化对地表沉降影响较为明显。

由图12可知,基坑周边地表最大沉降位移随降水井与地连墙深度比的增加而接近线性增加。当深度化比由27/31增加到35/31时,最大沉降位移由15.2 mm增加到23.5 mm,位移增加55%。由此可见,降水井与地连墙深度比对基坑周边地表沉降影响较大。

图12 地表最大沉降位移对比 Fig. 12 Comparison of maximum ground surface settlement displacement

3.2.2 地连墙水平位移

地连墙整体水平变形sh曲线如图13所示。墙身最大水平位移shmax随降水井与地连墙深度比的变化曲线如图14所示。

图13 地连墙水平变形对比 Fig. 13 Comparison of horizontal deformation of diaphragm wall

由图13可知,在降水井与地连墙深度比不同的条件下,地连墙整体水平变形规律基本相同,呈现“两端小,中部大”的分布特点，最大墙身水平位移出现在距地表13 m处,中部墙身(距地表7～23 m范围内)水平位移受降水井与地连墙深度比的影响较为明显。

由图14可知,墙身最大水平位移随降水井与地连墙深度比的增加而接近线性增加。当深度比由27/31增加到35/31时,墙身最大水平位移由27.8 mm增加到33.2 mm,位移增加20%。由此可见,降水井与地连墙深度比对墙身水平位移影响较大。

图14 地连墙最大水平位移对比Fig. 14 Comparison of maximum horizontal displacement of diaphragm wall

3.2.3 坑底隆起位移

坑底整体隆起变形如图15所示。由图15可知,在降水井与地连墙深度比不同条件下,坑底隆起变形的整体分布规律基本相同,表现为“中间小,两边大”的塑性变形分布特征，最大隆起变形出现在靠近地连墙位置,坑底中部的隆起变形略小于最大隆起变形。

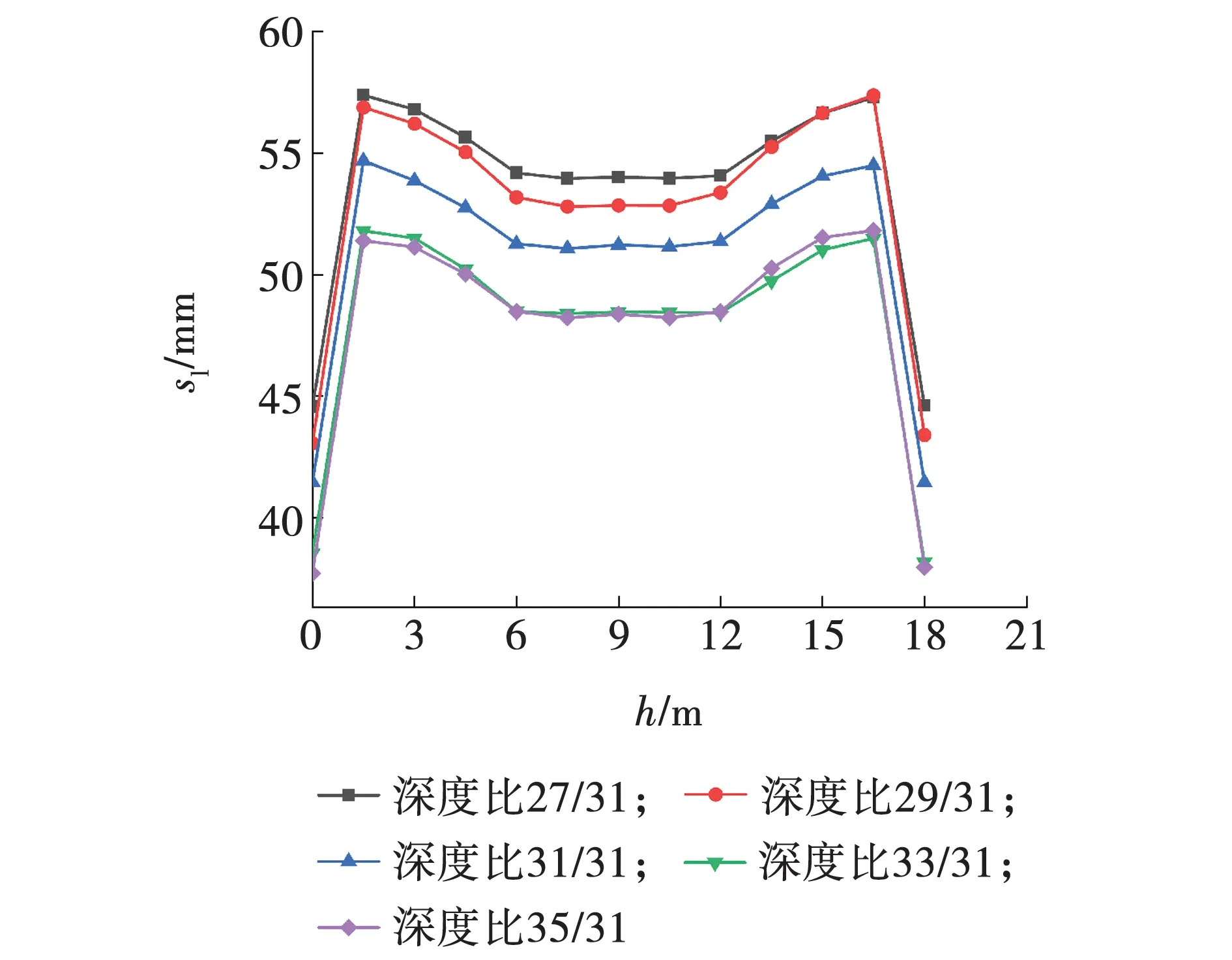
图15 坑底隆起变形对比Fig. 15 Comparison of heave displacement of pit bottom

坑底最大隆起位移随降水井与地连墙深度比的变化规律如图16所示。由图16可知,坑底最大隆起位移随降水井与地连墙深度比的增加而减小。当比值在27/31～29/31与33/31～35/31时,坑底最大隆起位移变化很小；当比值由29/31增加到33/31时,坑底最大隆起位移随比值的增加接近线性减小,最大隆起位移由56.8 mm减小到51.7 mm,位移减小9%。由此可知,降水井与地连墙深度比对坑底隆起位移的影响较小。

图16 坑底最大隆起位移对比Fig. 16 Comparison of maximum heave displacement of pit bottom

3.2.4 地连墙弯矩

地连墙弯矩图如图17所示。由图17可知,在降水井与地连墙深度比不同条件下,墙身弯矩分布情况完全相同。墙身最大正弯矩位于距地表13 m处,最大负弯矩值位于距地表7 m处。

图17 地连墙弯矩对比 Fig. 17 Comparison of bending moment of diaphragm wall

墙身最大正弯矩随降水井与地连墙深度比的变化曲线如图18所示。由图18可知,墙身最大正弯矩随降水井与地连墙深度比的增加而增加。当比值由27/31增加到33/31时,墙身最大弯矩由91.2 kN·m增加到96.1 kN·m,位移增加5.4%;当比值由33/31增加到35/31时,墙身最大弯矩由96.1 kN·m增加到103 kN·m,位移增加7.2%。由此可见,降水井与地连墙深度比对墙身弯矩影响较小。

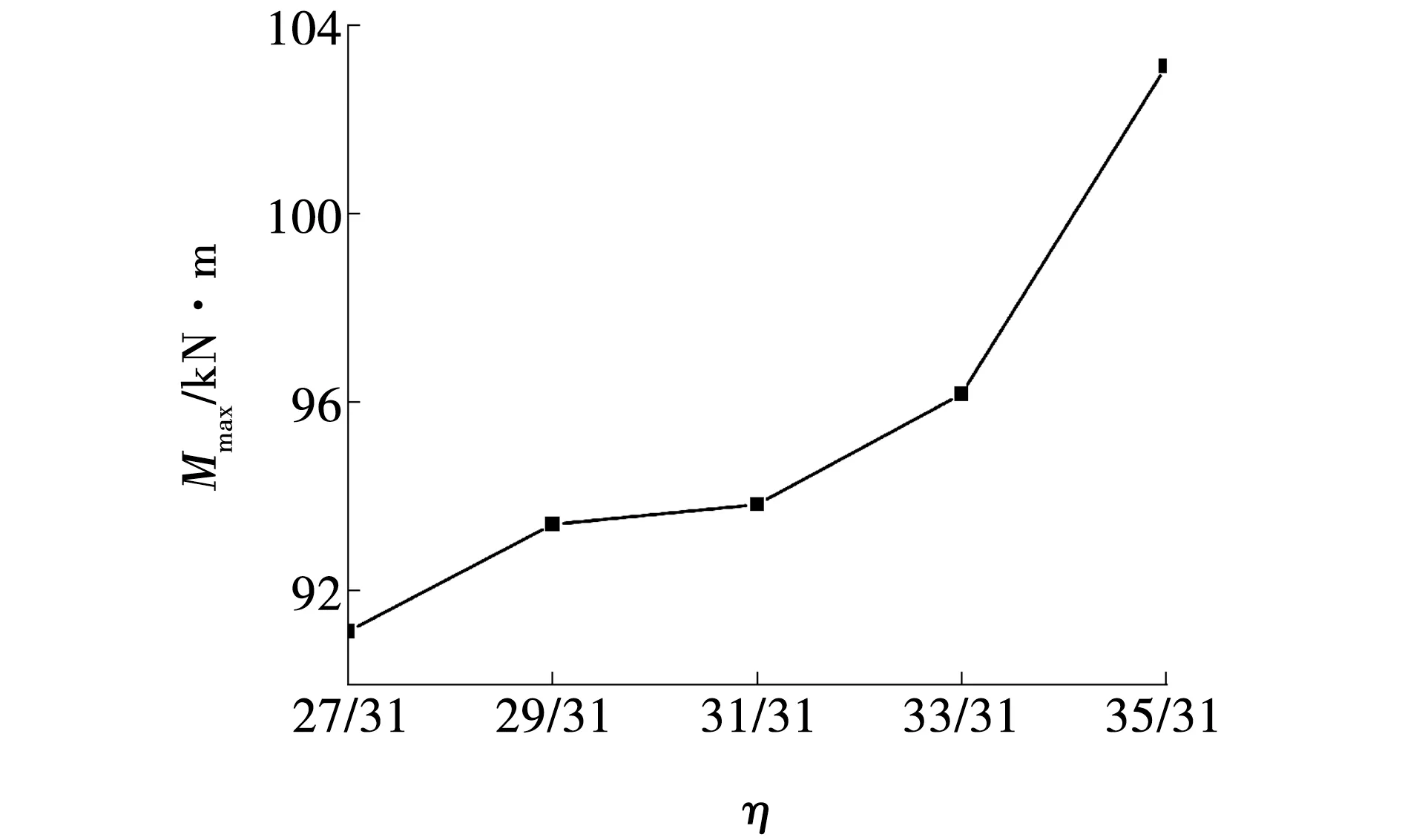
图18 地连墙最大弯矩Fig. 18 Maximum bending moments of diaphragm wall

4 结 论

(1)基坑周边地表沉降位移、地连墙水平位移和墙身弯矩皆随地下水初始水头的降低而减小,随降水井与地连墙深度比的增加而增加。坑底隆起位移随地下水初始水头的降低而增加,随降水井与地连墙深度比的增加而减小,但受二者的影响均较小。

(2)地下水初始水头在2.0～5.0 m范围内变化时,坑外地表沉降位移受影响较大;在8.5～11.0 m范围内变化时,地连墙水平位移受影响较大。地下水初始水头变化对墙身弯矩的影响很大,且接近线性变化,初始水头由2.0 m降低到11.0 m,墙身弯矩减小92%。

(3)降水井与地连墙深度比对基坑周边地表沉降位移与地连墙水平位移的影响较大,且接近线性变化,深度比由27/31增加到35/31,地表最大沉降增加55%,墙身最大水平位移增加20%。