异型阴极不同尺寸的凹槽对铝液阻力损失的影响

王瑞雪

(贵阳铝镁设计研究院股份公司，贵州 贵阳 550081)

0 引 言

异型阴极铝电解槽被提出以来，实践表明，其在铝电解槽节能方面具有优异的潜力。异型阴极铝槽节电的实质是由于异型阴极的阻流作用，使铝液波动减小，从而可以降低极距和槽电压，进而减少输入电能，达到节能电的目的。为了了解不同尺寸“沟”对铝液流经后阻力损失大小的影响，通过建立物理模型并用fluent模拟，通过后处理得出结果，比较分析得出结论。

1 二维管内湍流计算方法

对铝电解槽的流场的计算，国内外学者采用了多种数学模型，但大都采用求解k-ε二方程紊流模型来求解Navier-Stokes方程。

由湍流运动的特点结合物理模型，可以容易得到管内湍流的运动基本方程：

(2)动量方程

1.1 问题描述

为了了解不同尺寸凹槽对阻力损失大小的影响，建立简化的模型进行模拟对比。简化的模型如下：950 ℃的铝液流经二维通道，形状见图1，尺寸及入口速度见表1。试应用数值计算方法求解铝液流经二维通道时的流速分布和静压分布，并获得流经300 cm时的阻力损失。

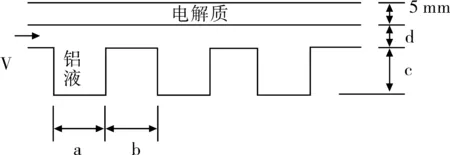
图1 沟形状Fig.1 Shape of the grooves

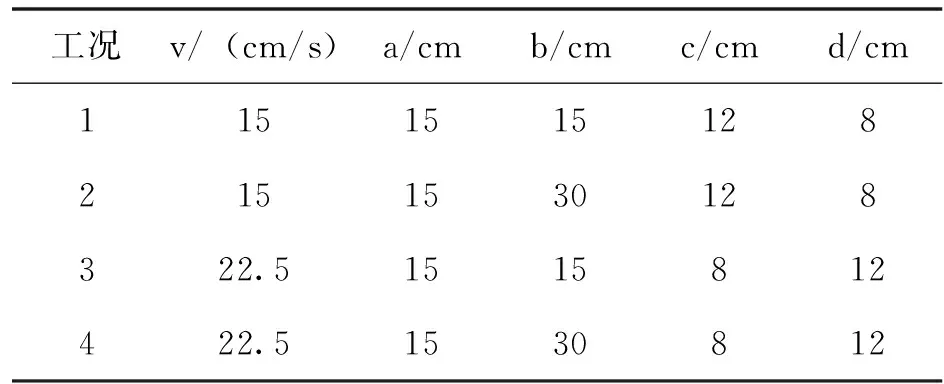
表1 不同凹槽的尺寸及入口速度Tab.1 Sizes and inlet speeds of different grooves

1.2 物性参数

查相关文献知铝液的物性参数如下：

λ=59.9+0.03T

ρ=2 613-0.262T

代入温度T=950+273.15=1 223 K计算得：λ=96.594 5w/m·K，ρ=2 292.56kg/m3，μ=0.75 546×10-3kg/m·s，比热取推荐值Cp=1 181J/kg·K。

查相关文献知电解质物性参数如下：

λ=0.045 4w/m·K，ρ=2 050kg/m3，μ=0.003kg/m·s，比热取推荐值Cp=1 760J/kg·K。

1.3 湍流强度

代入数据得I=0.051=5.1 %；

2 二维管内湍流计算模型

我们对凹槽内的流场计算进行一定的简化后，得出的计算模型如下所示：

2.1 物理模型

利用gambit建模，见图2。

在gambit里面建立模型，考虑进出口情况，将进出口适当延长1～2 m；

分别取步长0.005 m、0.01 m划分网格。

指定边界条件类型，通道入口为velocity inlet，出口为outflow，交界面为interface，电解质表面边界条件设为wall，其他边界保持默认的wall；

指定区域流体类型，区域1为铝液，区域2为电解质。

输出mesh网格文件。

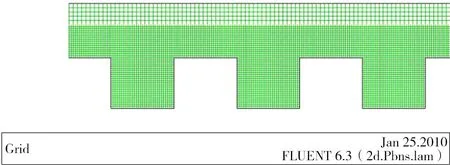
图2 网格划分Fig.2 Grid division

2.2 数学模型

利用fluent进行仿真计算

由于所计算的二维通道流动问题，故选择二维单精度求解器即可满足要求；

导入网格文件并检查，没有出现负体积，且计算域大小符合所要进行分析的计算域尺寸，故无需重新划分网格，可以直接用于计算；

选择计算模型，选多相流VOF模型，由前面的计算可知，从通道入口到出口，即全流场都是高雷诺数的湍流流动，且由于模型有较高的稳定性、经济性和计算精度，适合于高雷诺数湍流，故粘性模型使用双方程模型；

对于操作环境，考虑重力的影响，设置Y=-9.81；

定义流体的物理性质，代入950 ℃铝液和电解质的物性参数；

设置边界条件，代入入口速度值v m/s，其他均采用默认边界条件；

设置求解参数，求解flow和turbulence方程，由于本题使用的是结构化网格，精度要求相对较低，故选择一阶迎风格式；

选择compute form为inlet对流场进行初始化；

打开残差监控，设置残差收敛标准为0.000 001，迭代2 000次计算。

3 计算结果与分析

3.1 不同情况下的速度分布和压力分布

为了解铝电解槽内部流动情况，取较稳定区域(取截面x=1.8 m和x=2.7 m之间的区域)，速度分布和压力分布详见图3-10。

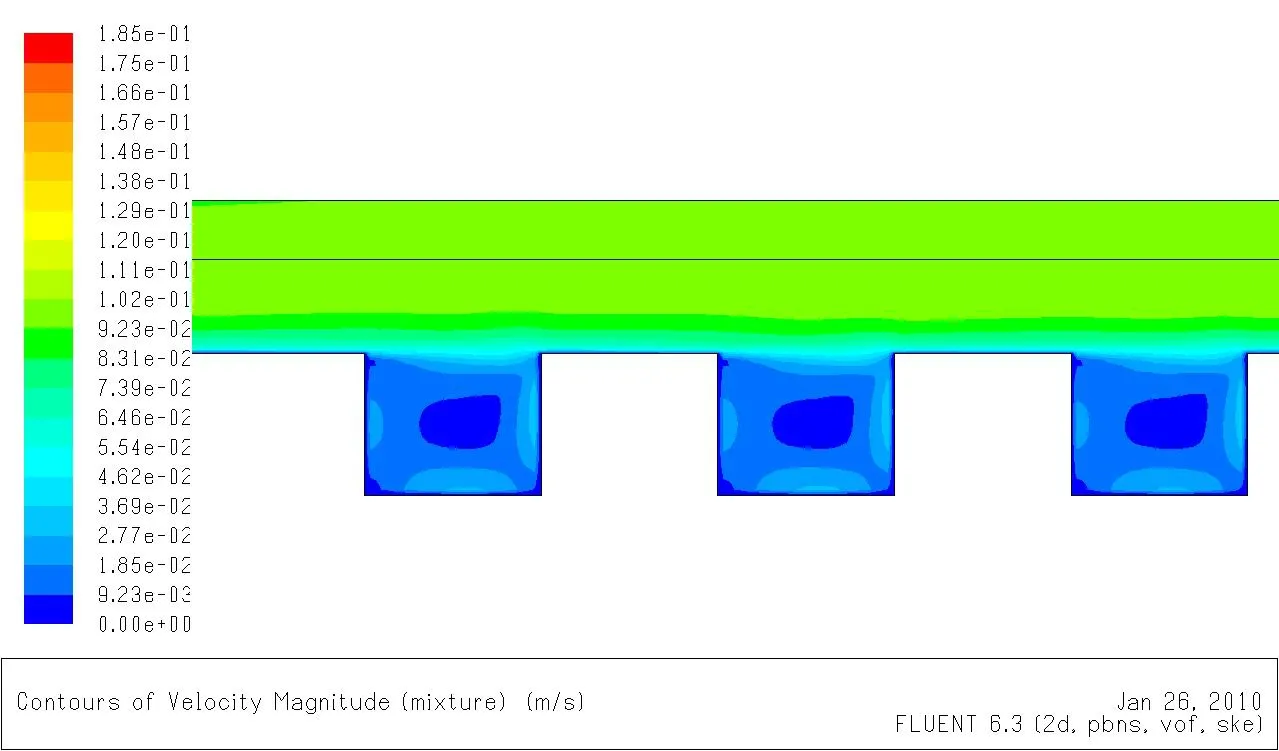
图3 情况1下的速度分布Fig.3 Speed distribution in condition 1

图4 情况1下的静压分布Fig.4 Hydrostatic pressure distribution in condition 1

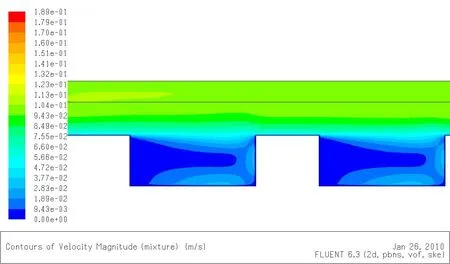
图5 情况2下的速度分布Fig.5 Speed distribution in condition 1

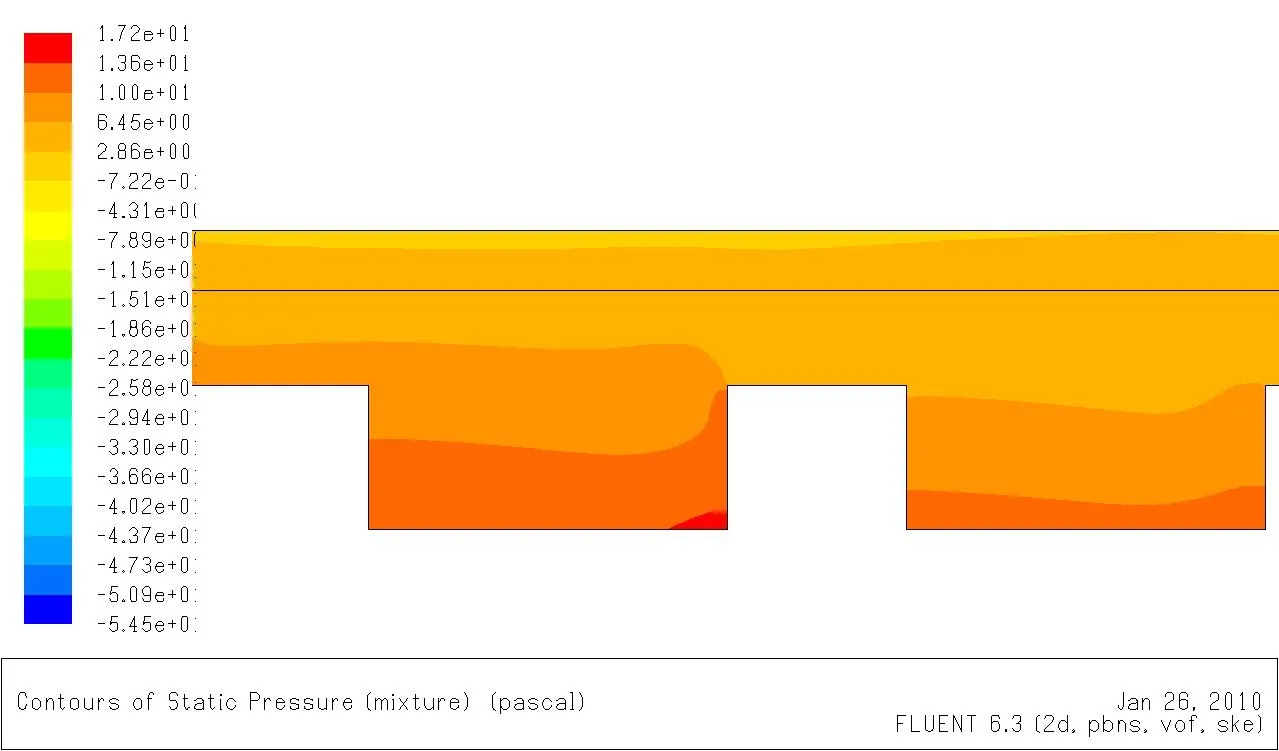
图6 情况2下的静压分布Fig.6 Hydrostatic pressure distribution in condition 2

图7 情况3下的速度分布Fig.7 Speed distribution in condition 3

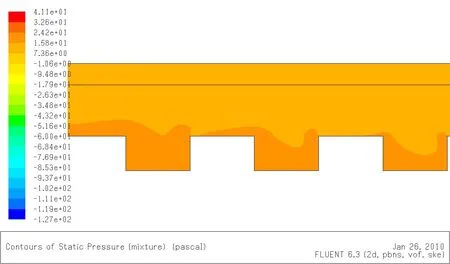
图8 情况3下的静压分布Fig.8 Hydrostatic pressure distribution in condition 3

图9 情况4下的速度分布Fig.9 Speed distribution in condition 4

图10 情况4下的静压分布Fig.10 Hydrostatic pressure distribution in condition 4

3.2 不同情况下截面x=1.8 m的速度分布

不同情况下截面的速度分布详见图11。

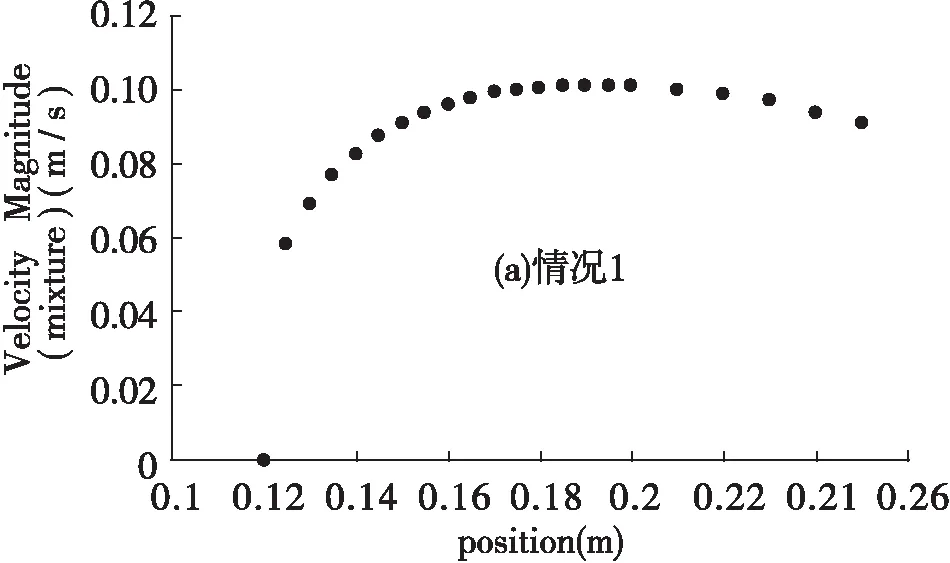
图11 不同情况下截面x=1.8 m处的速度分布图

3.3 结果分析

取3 m计算结果，其中x=2.7 m处为截面1，x=3.6 m为截面2，用求解器求得平均压力列于表2。

表2 不同情况下截面1和截面2的平均压力/PaTab.2 Average pressure of section 1 and 2 in different conditions/Pa

通过比较分析得知：情况4下的阻力损失最大。由于阻力越大，铝液的流动越小，越稳定，故可知工况4的设计最符合工程要求。

4 结 语

(1)通过建立凸台凹槽二维通道的物理模型，利用FLUENT软件很好的模拟了通道中的流动情况，从仿真结果来看模拟结果较好地验证了管内流动发展的真实情况。

(2)通过比较4种不同的物理模型发现，在铝液高度一定的情况下，凹槽尺寸为30×8 cm时，阻力损失最大，由于阻力越大，铝液流动也越小，越稳定，故凹槽应采用这种物理模型较好。

(3)在fluent中将进口设置为速度进口，而在实际情况下是铝液受电磁力作用而运动，从而引起电解质运动，在fluent中采用给定速度来模拟可能存在一定的问题，还应进一步改进，才能得到更精确的结果和更准确的结论。