浅析平面向量的应用

■谭先美

平面向量作为一种基本工具,在研究数学与物理问题中都有极其重要的作用,尤其是平面向量的几何意义,又有很多独特之处,若在解题中能合理应用,必能起到化难为易,化繁为简的作用。

一、平面向量在平面几何中的应用

用向量方法解决平面几何问题的一般步骤:建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量问题;通过向量运算,研究几何元素之间的关系;把运算结果“翻译”成几何关系。

例1 如图1,在正方形ABCD中,P是对角线BD上的一点,四边形PECF是矩形,用向量法证明:PA⊥EF。

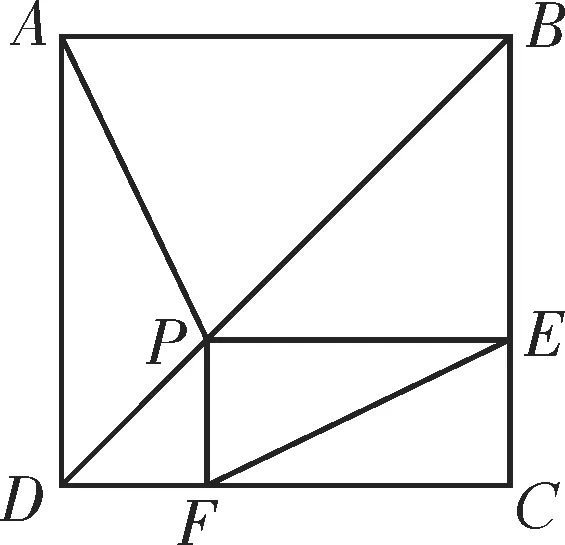
图1

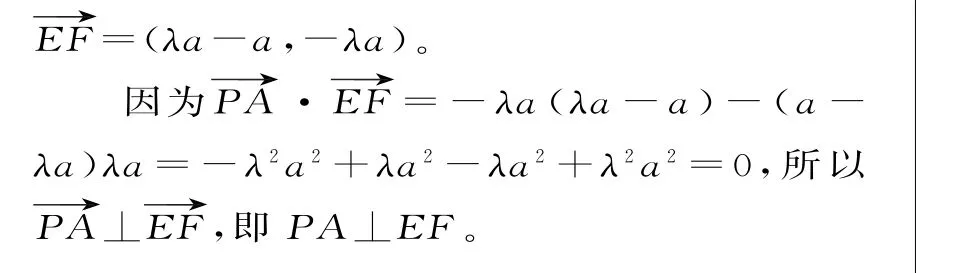
二、平面向量在物理中的应用

用向量法解决物理问题,要充分利用向量的三角形法则与平行四边形法则将物理问题转化为数学中的向量问题,正确地作出图形以便帮助求解。

例2 在风速为75(6- 2)km/h的西风中,飞机正以150km/h的速度向西北方向飞行,求没有风时飞机的飞行速度和航向。

解：设风速为v0,有风时飞机的飞行速度为va,无风时飞机的飞行速度为vb,则va=vb+v0,且va,vb,v0可构成三角形(如图2)。

图2

故没有风时飞机的飞行速度为150 2km/h,航向为北偏西60°。