耦合融雪的新安江模型在干旱区径流模拟研究

张梅洁， 吕海深， 刘 娣， 朱永华， 孙铭悦

（1.河海大学水文水资源与水利工程科学国家重点实验室，江苏 南京 210098；2.河海大学水文水资源学院，江苏 南京 210098）

中国西北地区的河流多发源于山区，冰雪融水是河流春季的重要补给来源［1］。西营河位于甘肃省境内，其径流主要来源于祁连山东段融雪和山区降水。在西营河流域，多数研究侧重于西营灌区的生态及水利建设，进行水文模拟极少，迫切需要探索适用于该区域的水文模型。在该流域范围内使用水文模型进行模拟时，需要考虑春季融雪的影响。Wu［2］等通过研究长序列融雪径流过程，完成了融雪组分的评估，指出春夏季融雪径流比例随气候变暖而有所改变，融雪过程会影响高寒山区水文过程。李志龙［3］在研究资料缺乏的寒区流域水文模拟中，将改进的新安江模型作为混合模型的一部分，进行了融雪径流的模拟。目前，关于融雪径流预测已经有应用较广的模型，如SRM模型［4］；此外还有包含融雪模块的模型，如SWAT 模型［5］、MIKE SHE 模型［6］等。然而，SRM 模型主要对于春季融雪模拟较好，多数只能应用于年内短期的径流预报［7］。SWAT 模型与SHE模型又较为复杂，输入的数据需要包含大量信息（包括数字高程数据、土地利用数据、积雪覆盖特征、土壤特征、降水气象数据等）［8］，在西营河这种数据较为缺乏的流域，数据搜集困难且数量较少，代表性不强。故而需要探索更加适用于西营河流域的融雪径流模型。

新安江模型［9］作为国内应用较广的模型之一，其模型结构清晰、层次分明，在实际应用中得到不断地完善，可以通过改进的模型进行数据缺乏地区的水文模拟。刘金涛等［10］总结了新安江模型发展的特点，主要是架构形式趋于多样性、产汇流模型不断物理化、应用范围不断延伸。Lyu 等［11］采用粒子群算法和集合卡尔曼滤波数据同化的3 种变化，对罗江和资料匮乏地区进行模型参数批量估计。韩元元等［12］将变动态存储系数法结合新安江模型进行河道洪水演算。以上研究说明在模型驱动数据及方法上均可与新安江模型进行配合，从而提高模型的应用范围及模拟效果。Alazzy［13］采用不确定性估计（GLUE）方法，对中国新安江模型估算月径流的不确定性进行检验和预测，发现采用Nash效率系数评估的新安江模型的参数不确定性更小。据此，本文率定参数时，主要以Nash 效率系数作为率定参数时的目标函数。邓元倩等［14］、邵成国等［15］分别将新安江模型应用于沣河流域、新疆乌鲁木齐河，模拟效果较好，说明新安江模型适用流域逐渐扩大到西北地区，不再仅仅局限于湿润地区。赵兰兰等［16］根据干旱地区实际情况，将超渗产流模式加入新安江模型在拒马河流域进行了暴雨洪水预报及对比分析，在新安江模型各层次内部使用的方法可根据流域的地理位置等条件进行适当改进。至此，超渗产流与新安江模型的融合，使新安江模型突破了原有的固化模式，从最根本的产流层次进行改进，加强了新安江模型在全国多地的适用性。姜卉芳［17］最早将融雪径流模拟加入新安江模型应用于切德克流域，随后田龙［18］等人在该版本基础上考虑能量概念进行高寒山区融雪径流模拟。然而，该模型仍需对太阳辐射、地形影响、积雪面积等进行大量分析，在资料缺乏的山区应用较难。本文选取应用广泛、层次结构化清晰的新安江模型，在其中加入仅以气温为主要阈值的融雪模块，从而扩大新安江模型的适用范围。

在资料匮乏地区，如西营河九条岭站以上流域无降水观测，且流域内地形差异大，九条岭水文站降水无法代表全流域情况。较为准确的降水驱动数据对水文模拟具有重要意义，直接影响水文模拟精度。在模拟时，需要选取最适合的驱动数据。孙铭悦［19］等在进行水文模型模拟时，比较了站点数据和格点降水数据的模拟效果，得出格点降水比站点平均的降水数据更好。本文首先进行格点降水数据修正，随后将融雪模块与新安江模型耦合，利用修正后的降水数据驱动耦合模型进行径流模拟。

1 研究区概况与方法

1.1 研究区概况

西营河位于武威市西南部，是石羊河流域的一条支流，上游由宁昌河和水关河组成，发源于祁连山东段冷龙岭。西营河属于高寒半干旱半湿润气候区。径流主要由高山融雪以及祁连山区降水组成。西营河多年平均出山径流达3.184×108m3，位列石羊河上游八条河流之首，占比22.3%。出山口附近设有九条岭水文站，也是该流域出山口以上唯一的水文测站。九条岭站以上区域植被良好，水土流失轻微，此处与上游由于地势的差异，降水差别较大［20］。上游年降水量可达500～800 mm，九条岭站年降水量仅为200～400 mm。流域4—5月多为春季融雪径流，6—9月径流为山区降水产生。本文主要研究区为西营河九条岭站以上流域（图1），集水面积为1077 km2。该站是石羊河流域的八大河流中不受人工设施影响的水文测站之一，积累了长序列水文实测资料。

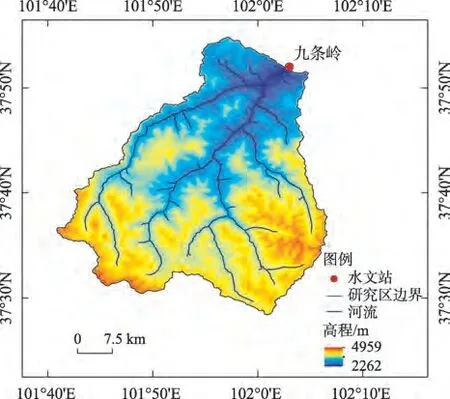
图1 研究区域示意图Fig.1 Schematic diagram of the study area

1.2 数据来源

本文改进的新安江模型输入的降水和气温数据采用国家气象信息中心发布的数据集。降水采用中国地面降水日值0.5°×0.5°格点数据集（V 2.0），代码为SURF_CLI_CHN_PRE_DAY_GRID_0.5。气温采用中国地面气温日值0.5°×0.5°格点数据集（V2.0），代码为SURF_CLI_CHN_TEM_DAY_GRID_0.5。此外，九条岭水文站2011—2018 年的逐日蒸发和逐日流量资料来源于中华人民共和国水文年鉴第10卷第5册甘肃河西地区内陆河水文资料。

1.3 研究方法

1.3.1 格点降水数据修正方法 格点数据集主要由中国地面高密度台站的降水结合薄盘样条法制作，依托于站点数据，插值时存在一定误差。数据集（V 2.0）制作人赵煜飞［21］对该数据集进行精度评估时指出，夏季误差较其他季节较为明显。将格点降水数据用于降水（融雪）径流模拟时发现在夏季会出现少量径流异常值，需要进行降水数据修正。经试验，未经修正的格点降水，在研究区每年都会出现少数的异常情况，径流未出现峰值，然而作为径流主要成因的降水却出现较大值，且与序列前后日突变较大，与临近站点降水及相关记录比较发现此日并非暴雨日且前后日并无较大降雨，从而考虑应是数据集制作产生的误差导致。常用的修正方式是与附近站点序列进行比较。然而，在西营河流域，附近的气象站点距离流域较远（图2），且分布多偏东北、西北方向，作为降水产流主要来源的西南部山区没有代表性测站，无法全面展现整个流域降水、气温等情况。

图2 西营河流域邻近气象站点分布Fig.2 Distribution of meteorological stations near Xiying River Basin

本文探索性尝试通过年最大降水和径流系数进行约束，筛选出每年的异常格点降水值进行修正，从而提高径流模拟的精度。经过多年格点降水径流模拟试验，归纳得出以下降水量和径流系数两个约束能检测出较明显的格点降水异常数据。同时违背降水量约束（公式1a）和径流系数约束（公式1b）两个约束条件判断为异常点：

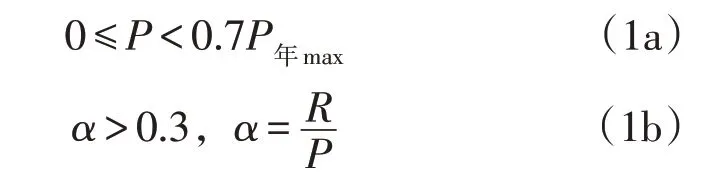
式中：R表示出口九条岭水文站日尺度实测径流深（mm）；P为逐日格点降水值（mm）；α为径流系数，径流系数0.3 的约束条件主要是采用3σ原则，通过正态分布置信区间算出，即平均年径流系数为0.503，标准差σ为0.067，在小于μ-3σ即0.3 时，概率仅为0.27%，认为该测量值为坏值。

尽管下垫面条件和气候条件的复杂性会对不同自然地理条件的降水-径流关系产生一定影响，降雨和径流仍具有较强的成因关系，可以作为两个序列的初步评定参考。本研究识别出异常点后，利用降水和径流相关关系进行修正，将识别出的异常点修正到每年绘制的剔除异常点的降水-径流相关关系图上，具体流程如图3所示。

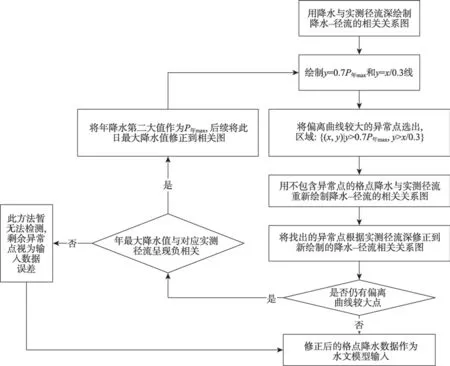
图3 格点降水异常点识别与修正流程Fig.3 Grid precipitation anomaly identification and correction process

某些年份单日格点降水最大值达到40 mm甚至更大时，若此点为异常点，会影响降水量约束的异常点挑选，检测时遇此情况，需要以年第二大降水值作为降水量约束的基础值，再乘以试验率定出的比例系数0.7。

1.3.2 融雪模块与新安江模型耦合 本文在新安江模型基础上，增加了融雪模块，主要包括融雪模块、蒸散发计算、蓄满产流计算、三水源划分和汇流计算。

（1）融雪模块

改进后的新安江模型在第一层次前，加入融雪模块，主要采用度日因子法进行融雪计算。度日法假设融雪量与气温为显著线性关系，其计算公式如下：

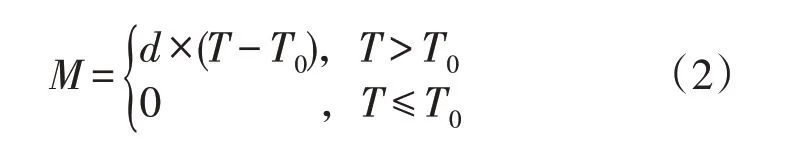
式中：M为融雪水量（mm·d-1）；d为度日因子（mm·℃-1·d-1）；T0为融雪临界温度（℃）；T为气温（℃）。

在融雪模块中，主要输入数据为气温和降水。积雪消融的能量主要来源于净辐射和感热通量，其中，净辐射包含长波辐射和短波辐射。冰雪消融以近地表层的长波辐射和感热通量原因为主，气温又是地表长波辐射的主要影响因素，从而本方法将能量的影响直接由较易获取的气温作为模型的驱动。加入融雪模块后，将融雪水量和降雨量综合的液态水作为后续模型的输入。

（2）蒸散发计算

模型采用三层蒸发模式，其中，蒸散发能力使用蒸发折算系数与九条岭水文站观测值的乘积。

式中：EP为蒸散发能力（mm）；KC为蒸散发折算系数；Epan为蒸发皿观测蒸发（mm）。运用的主要思想是土壤蒸发能力与相同气象条件下的水面蒸发一般呈线性关系。

（3）蓄满产流

蓄满产流模式为包气带达到田间持水量的产流模式。概化为达到田间持水量后，才开始产流。由于流域各处蓄水能力不同，降水与初始包气带蓄水量之和小于流域包气带蓄水容量最大值时，为流域部分面积产流。同理，降水与初始包气带蓄水量之和大于流域包气带蓄水容量最大值时为全流域产流。具体计算公式如下：

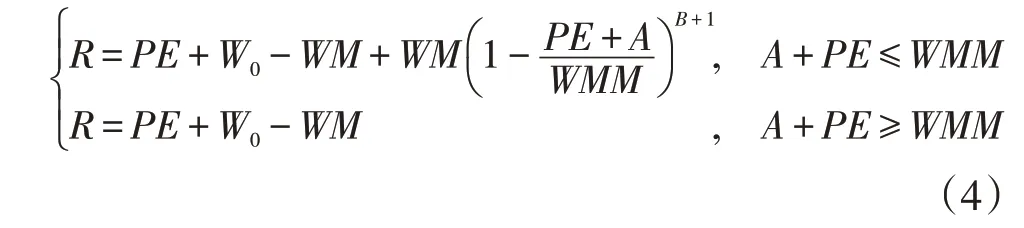
式中：A为流域初始包气带蓄水量所对应的纵坐标值（mm）；WMM为流域单点最大蓄水容量（mm）；WM为流域任一点的包气带蓄水容量（mm）；B反映流域包气带蓄水容量分布的不均匀性，B越小表示越均匀；R为产流量（mm）；W为流域蓄水量（mm）。值得注意的是，PE中的P指的是融雪计算后的液态水量（mm）。

（4）三水源划分

产流量的划分延续传统新安江模型的思路，分为地表径流、壤中流和地下径流。考虑产流面积的影响和下垫面条件，采用与上一模块包气带蓄水容量分布不均类似的处理，仍将产流面积上的自由水容量分布用抛物线近似。其中，自由水是毛管水和重力水的合称，是在土壤中受力的作用可以自由流动的水。

（5）汇流计算

地面径流直接流入河网，计算公式如下：

式中：QS为地面径流汇流（m3·s-1）；RS为地面径流（mm）；U为单位转换系数，为常数；i指日数，时间尺度为日尺度。

壤中流汇流采用线性水库法，计算公式如下：

式中：QI为壤中流汇流（m3·s-1），CI为壤中流消退系数，RI为壤中流径流（mm），U 为单位转换系数，为常数。

地下径流汇流仍采用线性水库法，采用公式如下：

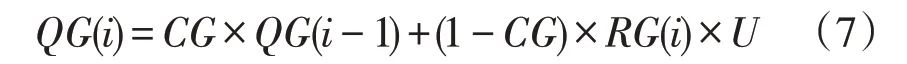
式中：QG为地下径流汇流（m3·s-1）；CG为地下水消退系数；RG为地下水径流（mm）；U 为单位转换系数，为常数。

1.3.3 评估准则 根据水文预报评价标准，采用相对误差RE和确定性系数DC进行评价。二者公式如下：

2 结果与分析

2.1 格点降水数据修正结果分析

根据流域在降水网格的位置，提取流域内格点降水。经过格点降水异常点识别与修正方法进行修正（图3）。在约束条件所构成的区域内寻找异常点，每年需要修正的格点并不多，但这些格点属于偏离降水径流成因关系曲线较大的降水数据点。由2018 年的格点降水的修正可以看出（图4），2018年仅有两日的格点降水需要修正，即红色标注部分（图4a），将异常点处的降水数据修正到剔除异常点后的降水-径流关系曲线上（图4b），这两个异常点的降水值分别由24.3 mm、21.8 mm修正为0.6 mm和4.3 mm。修正后，率定期的模拟效果确定性系数从0.59 提升到0.63，提升了0.04。验证期的模拟效果确定性系数从0.69 提升到0.72，提升了0.03（表1）。2013 年的格点降水修正对确定性系数的提升较为明显，从0.23 提升到了0.69。格点降水修正对于75%的年份均表现为模拟效果提升。

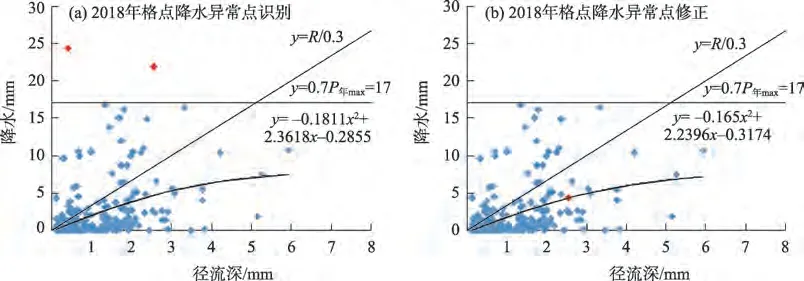
图4 2018年格点降水的修正Fig.4 Grid precipitation correction in 2018

2.2 融雪径流模拟分析

分别用融雪模型融合前后及降水修正后的新安江模型进行模拟，模拟效果见表1。由表1 可知，融雪模块耦合后的模拟结果通常比传统的新安江模型模拟得更好。可以注意到，改进过程中，确定性系数的提高和相对误差的降低并不同步，这是由于在参数优化时，选择了确定性系数作为目标函数，其更能反应模拟过程，体现流量模拟值的变化在总体变化中的比例。而相对误差更多地评价模拟总流量与实测值之间的关系，重点在总量的控制上。除2013 年由于以确定性系数为目标函数的参数优化使得确定性系数大幅提升，相对误差为23%，超过了20%外，其余年份的各种情况模拟，相对误差均在20%以下，在后续研究中若能继续进行多目标参数优化，有望将2013年的相对误差进一步降低。

表1 不同情况下新安江模型模拟结果Tab.1 Simulation results of Xin’anjiang model under different conditions

选择2011—2016 年作为模型率定期，2017—2018年作为模型验证期。率定期参数优化后，确定性系数达到0.63，此套参数用于验证期，确定性系数为0.72。说明此模型在西营河流域具有一定适用性。经过融雪模块融合、格点降水修正，87%以上的模拟年确定性系数在0.6以上、62%以上的年份模拟达0.69以上，模拟结果较好。新安江模型平均确定性系数为0.62，融雪耦合和格点降水修正后平均确定性系数为0.67，提高0.05。将变动态存储系数法用于新安江模型河道洪水演算的研究在印江河流域只提高了0.0182［12］；改进新安江模型在乌江独木河流域模拟时确定性系数仅提高0.02［22］。与类似研究相比，本文运用改进的新安江模型在西营河流域的平均确定性系数提高0.05，效果显著。

采用2011—2016年进行参数优化模型率定，利用2017—2018年进行模型的验证，参数率定时采用遗传算法优化参数，其中以确定性系数作为算法的目标函数进行率定，表2显示了优化后的模型参数。

表2 含融雪的新安江模型参数及物理意义Tab.2 The parameters of snowmelt-Xin’anjiang model and its physical significance

耦合融雪的新安江模型率定期和验证期模拟结果如图5所示，除第二年洪峰模拟偏低外，其余年份洪峰模拟效果均很好。率定期的多年模拟结果中，确定性系数达到0.63，比未进行格点降水修正的0.59 提高了0.04。在验证期，可以看到模型已模拟出春季融雪径流，夏季的洪水部分前期模拟较好，后期模拟效果较低，可能与当年的格点降水数据仍存在误差有关。验证期耦合融雪的新安江模型经降水修正后比新安江模型模拟的确定性系数提升0.05。

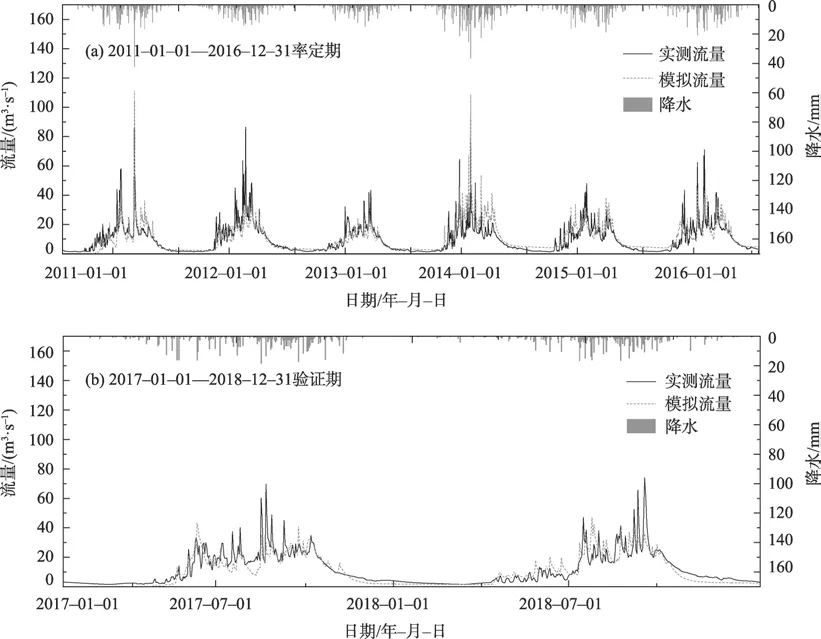
图5 模型率定期和验证期模拟结果Fig.5 Simulation results during model calibration period and validation period

在融雪径流的模拟过程中，率定期内，2011年、2013 年、2014 年、2015 年的春季径流模拟很好。在未出现较大降水时，也会出现春季小洪峰，此时主要是由于流域上游祁连山东段的山间积雪融化导致。如2011 年4 月20 日，此前4 d 及当天未出现降水，出现了13.8 m3·s-1的流量峰值。由于当时气温逐渐升高，山上的积雪逐渐融化，形成了此次春季非降雨成因的融雪径流。改进的新安江模型在夏季洪峰的模拟上效果很好，这可能是因为在西营河流域，产流层较薄，多数情况下当日降水会产生当日出流，流域汇流延时较短。在验证期，总体模拟效果普遍不如率定期，但春季径流仍然能够模拟较好，说明模型加入的融雪模块运用较好，以气温为基础足以计算出研究区的春季径流。2017 年的夏季洪水模拟较好，而2018 年7 月、8 月的径流，虽然趋势一致，但多出现模拟值较高的情况。对照降水数据可以发现，在2018 年修正的降水仅为9 月降水。这是由于在降水修正时，没有将非较大值的降水考虑在修正范围内，修正的两个约束并不能识别较小降水的趋势性问题，这也是在后续降水数据使用中，需要深入探讨的问题。

3 结论

本文考虑到研究区实际情况将新安江模型加入融雪模块，考虑融雪对径流的影响。另一方面，由于研究区水文站点少，采用格点降水和气温数据集作为改进的新安江模型的驱动数据。运用过程中发现异常点并进行了识别方法及修正方法的探索，将格点降水进行修正作为模型驱动，进行水文模拟，进而分析新安江模型改进前后、格点降水数据修正前后的模拟效果，得到如下结论：

（1）在站点资料缺乏的干旱半干旱区，利用全国范围内制作的气象数据集解决由于资料缺乏，数据集存在一定误差的问题，运用降水-径流关系曲线修正少数偏差较大的格点降水后，能够提高数据可用性，模拟的确定性系数在8 a 年中有6 a 均有提高，其余2 a差异不大。

（2）将融雪模块耦合新安江模型，使用的模型驱动数据较少，运用简单。新安江模型在西营河流域模拟流量过程的年确定性系数均在0.5 以上，经过融雪耦合和格点降水修正后87%以上的模拟年确定性系数0.6以上、62%以上的模拟年确定性系数达0.69 以上。新安江模型平均确定性系数为0.62，融雪耦合和格点降水修正后平均确定性系数为0.67，提高了8%。总体模拟效果较好，在西营河流域运用良好。