基于Attention-LSTM-Kalman 建模的风洞动态流量软测量
周隽杰,付东翔
(上海理工大学光电信息与计算机工程学院,上海 200093)
引言
风洞作为气体流量次级标准装置,主要用于模拟真实环境下的气体流动[1]。风洞实验是研究空气动力学中的关键一环,不仅对航空与航天工程的发展起着重要作用,在交通运输、风力发电等方面也有广泛应用。动态流量是风洞实验中的一项重要参考指标,对于评价系统动态特性有重要意义。目前我国有一些流量仪器生产厂家宣称其产品已通过风洞流量标定,实际上他们标定的仅仅是平均流速,再计算出流量,但用固定的平均流速点来测流量精度不高[2]。且大部分流量仪都是在固定场所标定,很难考虑到不同环境下其他因素对流量的影响,测得流量的可靠性不强。在空气动力学研究日益发展的环境下,有必要研究高精度标准气体流量测量方法。软测量技术是根据某种最优准则,基于辅助变量和主导变量之间的数学关系构建的软测量模型[3]。它采用各种计算方法有机融合,实现待测参数及指标的测量[4]。该方法可以顾及更全面的样本数据,这对研究高精度风量动态测量有重要意义。
传统的软测量技术主要方法中,卡尔曼滤波是一种重要的方法,其动态性能好,但在噪声条件下,其状态估计与真实值的误差不易提出,测量精度受限。基于BP 神经网络的动态流量测量法[5],在一定程度上提高了在线测量精度,但简单的神经网络模型由于训练过程收敛速度慢[6],容易出现过拟合、稳定性差等问题。
随着深度学习的不断发展,其特点是可以从原始特征中获得更有效的多尺度特征,收敛速度更快,鲁棒性更好[7]。近年来涌现出深度网络模型有循环神经网络(Recurrent neural network,RNN)、门控循环单元(Gated recurrent unit,GRU)网络、长短时记忆神经(Long short-term memory,LSTM)网络等,其中,LSTM 网络因其对时间序列的强大学习能力,已成功应用于软测量领域。Ke 等[8]提出基于长短期记忆单元的软测量建模方法,有效地实现了工业过程中的动态测量。Yan 等[9]提出了一种基于Attention-LSTM 模型的河流流量预测模型,通过Attention 学习数据间的非线性关系,加强序列间的相关性,并有效提升预测精度。上述LSTM 模型方法只用作静态预测模型,其较长的训练、参数整定耗时,无法有效应用于动态瞬时流量测量。虽然离线训练的静态模型无需在线学习,但在动态性提取上有缺陷,导致估计精度低、鲁棒性差等问题[10]。另外,LSTM 模型存在当时间序列过长,序列中两个间隔时间步很远的样本之间相关特性不易发现等问题,考虑引入注意力机制。
本文基于LSTM 建立静态软测量模型,加入注意力机制,并结合Kalman 滤波,提出一种基于Attention-LSTM-Kalman 的动态测量模型。根据实验风洞环境特点,测量与气体流量相关的变量数据,对特征值进行归一化处理作为软测量模型的输入变量,并建立基于注意力机制的LSTM 预测模型,为了更好地适应系统的动态特性,加入Kalman 对输出进行动态调整。最后通过风洞测量实验验证该模型在动态测量中的可行性和有效性。
1 风洞流量软测量模型
本文为有效实现风洞流量动态测量,采用长短时记忆网络LSTM 作为预测模型,采集过去一段时间内的相关变量(压力、压差、温度和风速)作为输入,对时间序列中的流量进行预测,作为基本时间序列,此外引入注意力机制来更好地适应序列样本的相关性。图1 为本实验搭建的Attention-LSTM 建模过程。通过学习、训练和验证得到更精准的静态预测模型。
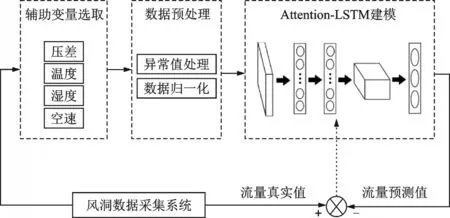
图1 Attention-LSTM 建模过程Fig.1 Modeling process of Attention-LSTM
1.1 LSTM 神经网络
通过应用LSTM,不仅可以建立顺序数据的短期关系,而且可以建立长期依赖关系[11]。LSTM 网络结构[12]如图2 所示,其引入了门控的思想,以保护和控制单元的状态,使网络能在多个时间步上继续学习。
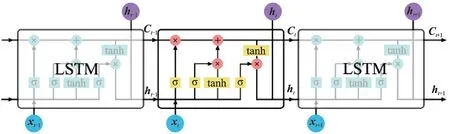
图2 LSTM 网络结构Fig.2 Structure of LSTM network
(1)遗忘门确定哪些信息从LSTM 单元状态中被丢弃,其输出表示为


C~t和ht在每个时间步都被转移到下一个单元,然后重复进行上述过程。
本文建立的LSTM 网络通过学习预测值和流量样本间的差异来学习权值和偏差,这种训练方式可以更全面地学习数据间的非线性关系。
1.2 注意力机制
由于多维辅助变量对输出的影响程度不一,可能对预测结果产生影响。对此本文用注意力机制[13]为不同时间步的输入分配权重来改善流量预测效果。主要原理是:保存时间序列输入经LSTM 网络产生的中间结果,将该结果与输出值联系起来,从而使模型学习如何选择性地关注数据,并为这些数据分配更合理的权重[14]。该网络结构如图3 所示。

图3 注意力机制工作步骤Fig.3 Work steps of attention mechanism
在t时刻得到LSTM 隐藏状态为:[ht,1,ht,2,…,ht,i,…,ht,T]T。
计算t时刻隐层状态hi对输出的注意力权重αt,i,本文采用点乘形式计算
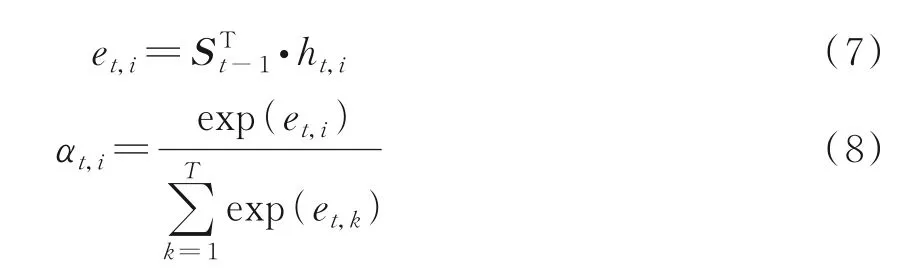
本文将注意力机制加入LSTM 神经网络,用于计算网络各隐层状态的权重,并建立Attention-LSTM 软测量模型实现风洞流量预测。
1.3 构建Attention-LSTM 网络模型
基于Attention-LSTM 的网络层结构如图4 所示,主要有4 部分组成。
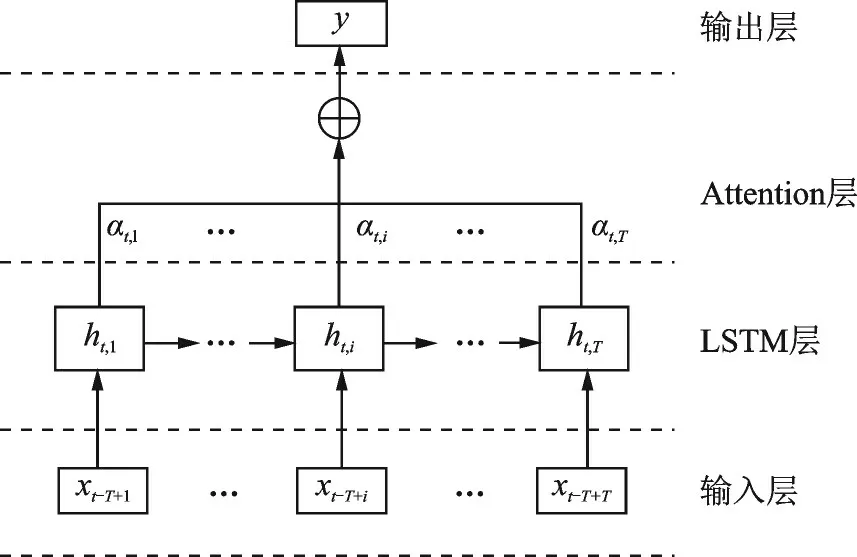
图4 基于Attention-LSTM 神经网络层级结构Fig.4 Hierarchy of Attention-LSTM network
输入层:输入为辅助变量时间序列和流量值。设T为时间步平滑窗口数,则在t时刻输入序列为

Attention 层:Attention 层的输入为上一层的输出ht,通过式(7,8)求得注意力权值αt,i,记t时刻该层的输出为St

输出层:选用激活函数为sigmoid 的全连接层,输出t+1 时刻的流量预测值y

2 卡尔曼滤波
考虑到被测系统的动态特性,且辅助变量的采集过程中产生的噪声和错误,上述建立的软测量模型本着“错进错出”的原理必然会对测量结果产生一定影响。针对该问题,提出在模型后使用卡尔曼滤波来消除影响。它运用递归算法来解决离散数据的滤波问题,并且不需要所有的先前数据[15]。具体方法如下:
(1)通过静态软测量法分析当前时刻的流量真值,由流量方程为

式中:Qk为k时刻的流量数据;S为截面积,这里取风洞洞口处截面;Vk为k时刻该截面上的空速。
(2)由于k时刻下该流量真值与软测量模型的预测值都被认为是不可信的,故依据卡尔曼原理对系统建模得到最优估计值。记Qj(k)为连续的静态软测量信号,Qd(k)为网络软测量模型软测量信号。选取Qd(k)作为Kalman 的测量信号,得到该系统的状态方程和测量方程分别为
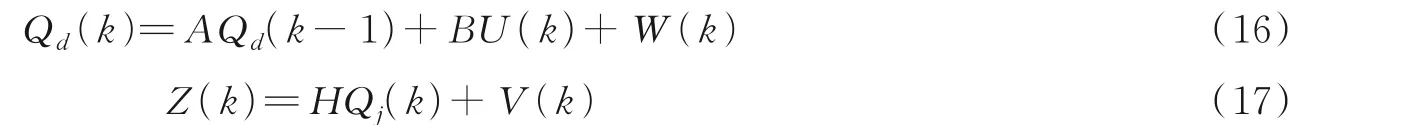
式中:A和B为系统参数;Qd(k)和Qd(k-1)分别为k时刻和k-1 时刻网络软测量模型得到的流量值;Qj(k)为k时刻分析的流量真值;U(k)和Z(k)分别为k时刻的控制量和观测值;W(k)和V(k)分别表示过程和测量噪声;H为测量系统的参数。
(3)经网络模型预测,Kalman 的输入输出都是一维流量数据,故取A=1,H=1,B=0。假设过程W(k)和测量噪声V(k)不随系统状态变化,为高斯白噪声,记其协方差分别为R、Q。采用k-1 时刻网络模型的流量输出作为k时刻的先验估计值并预测误差协方差P,则有

式中:P(k|k-1)为先验估计的协方差,P(k-1|k-1)为k-1 状态下的协方差。
(4)得到状态预测结果后,结合k时刻的网络模型流量输出Z(k),对先验估计值修正。得到当前时刻的最优估计值Qd(k|k)为

按照上述Kalman 算法流程实现对Attention-LSTM 软测量模型输出的动态校正,综合输出当前时刻流量的最优估计值。
3 实验分析
3.1 实验数据

根据式(15)可知,理想状态下的气体流量Q与流速v正相关,而根据伯努利方程可知,流速v与高度h,压强p,流体密度ρ有关。故本实验选取风洞出口截面处的压差、空速、温度和湿度作为预测流量的辅助变量,并使用标准流量计观测流量数据作为验证集。

3.2 实验结果
网络的输出值反归一化[17]后,转化为原始数据对应的输出。LSM 模型的流量预测结果如图5 所示。以原始四维变量为输入建立Attention-LSTM-Kalman 网络模型,其流量预测结果如图6 所示。
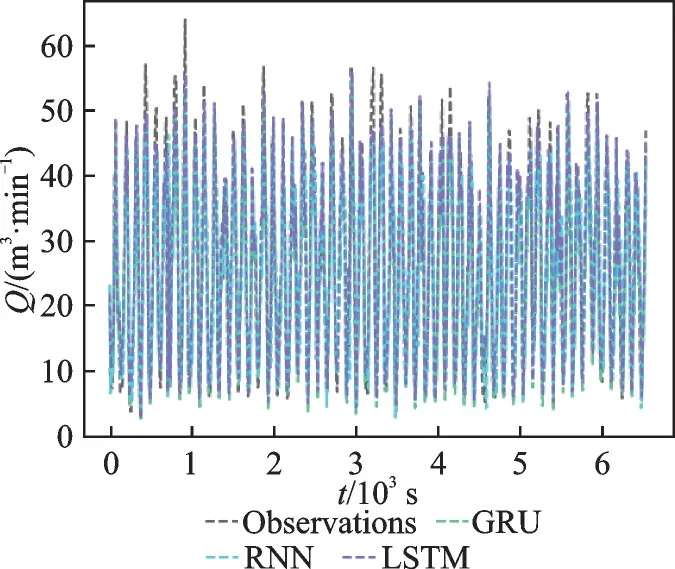
图5 流量真实值、GRU、RNN 以及LSTM模型预测值随时间序列的变化Fig.5 Change of real value, GRU, RNN and LSTM model predicted value with time series

图6 流量真实值、Attention-LSTM 以及Attention-LSTM-Kalman 模型预测值随时间序列的变化Fig.6 Change of real value, Attention-LSTM and Attention-LSTM-Kalman model predicted value with time series
模型预测的均方根误差(Root mean squared error,RMSE)和平均绝对误差(Mean absolute error,MAE)评价如图7、8 所示。静态预测模型Attention-LSTM 预测值的RMSE 和MAE 均低于GRU、RNN 和LSTM 模型,证明在本实验中基于注意力机制的LSTM 较其他两种时间序列模型 取 得 了 更 准 确 的 预 测 值 。 而 本 文 提 出 的Attention-LSTM-Kalman 模型的 RMSE 和 MAE 均低于Attention-LSTM 模型,经Kalman 动态调整后,模型的准确度明显提升,表明本模型有更准确的预测能力。
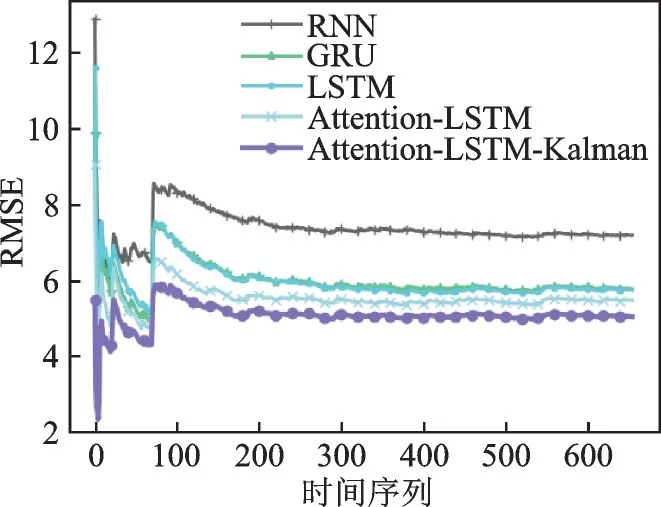
图7 RMSE 值随时间序列的变化Fig.7 Change of RMSE with time series

图8 MAE 值随时间序列的变化Fig.8 Change of MAE with time series
模型预测的确定系数R-squared 评价如图9 所示。静态预测模型Attention-LSTM 预测值的R-squared 比GRU、RNN 和LSTM 模型更接近于1,证明在本实验中,基于注意力机制的LSTM 模型的拟合度优于其他两种预测模型。而本文提出的Attention-LSTM-Kalman 模型的R-squared 高于Attention-LSTM ,静态预测模型经Kalman 动态调整后,R-squared 的值显著上升。这表明LSTM-Kalman 模型在预测方面具有更好的解释能力,Attention-LSTM-Kalman 模型更好地拟合了数据。各网络模型预测评价如表1 所示。
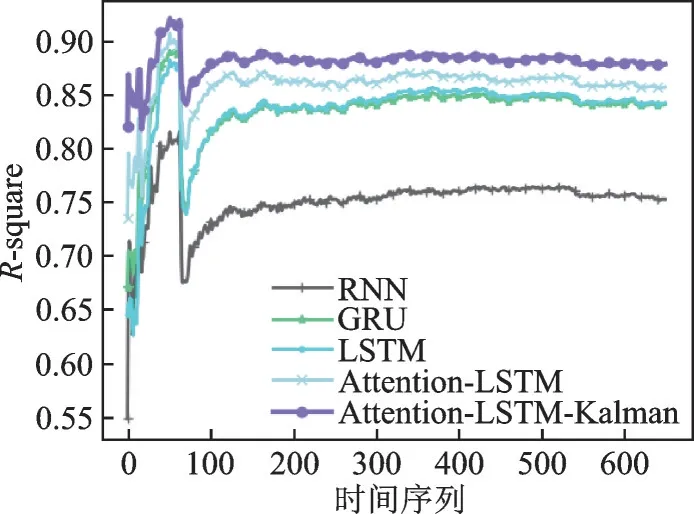
图9 R-square 值随时间序列的变化Fig.9 Change of R-square with time series
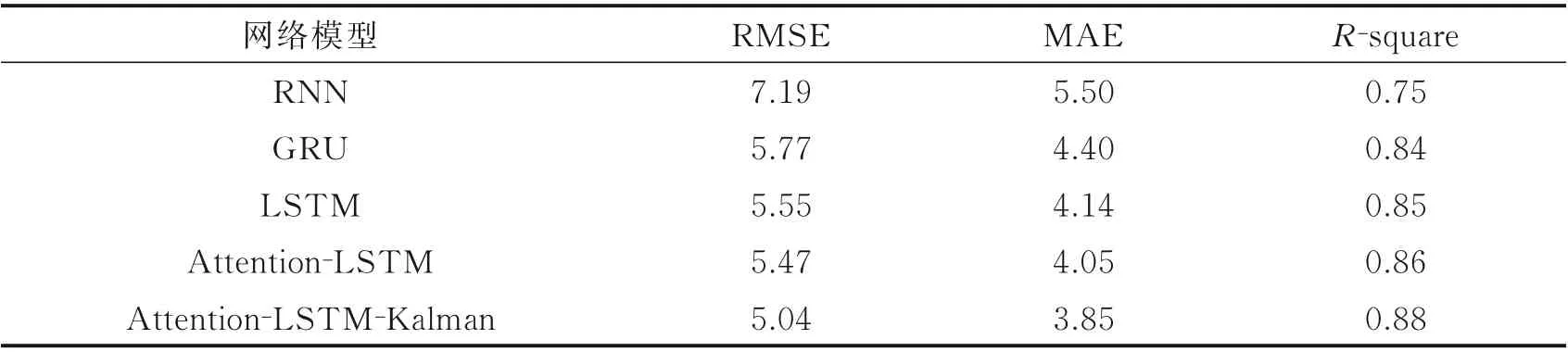
表1 各网络模型预测结果对比Table 1 Prediction results comparison of various network models
4 结束语
针对传统神经网络静态预测模型在动态流量测试中估计精度低,适应性差,不适用于动态测量场景的问题。本文提出一种动静结合的软测量方法,在静态预测模型后追加Kalman 滤波进行动态校正,使软测量模型能够取得更高的精度和拟合度,为了使序列间获得更好的相关性,本文也引用了注意力机制加以实现。实验结果表明,Attention-LSTM-Kalman 模型的动态测量值比RNN、LSTM 等传统预测模型的结果更加平滑且拟合效果更好,实现了流量动态测量,本文的模型方法对流量测量、标定等方面有参考意义。

