基于响应面法的锂渣旋流除泥优化研究

段耀旭 张悦刊 刘培坤 葛江波

(山东科技大学机械电子工程学院，山东 青岛 266590)

锂由于其独特的性质被广泛应用于锂电池工业和原子能等领域。随着新能源汽车的发展，锂的需求量也越来越大，2021—2025年仅锂电池产业需求锂资源总量约12.9万t，而生产1 t锂化合物随之产生的锂渣约有10 t[1]。锂矿通常伴生钽、铌等有价金属，在锂矿提炼过程中有价金属并未被完全回收，而存留在锂渣中。对锂渣中蕴含的有价金属进行综合回收利用，不仅符合环保政策要求且具有重要的经济意义。

锂渣中细泥含量较高，高含量的细泥对有价金属的提取会产生不利影响，因此需要对锂渣进行脱泥预处理。水力旋流器是一种按照密度、粒度进行分级或分选的装置，与其他设备相比具有占地面积小、分级效率高、可靠性高等优点[2]。宫振宇等[3]发现在入口浓度不同时，底流口直径对旋流器性能的影响规律不同;张玉龙等[4]指出，随着进料压力的增大，溢流产率增大;冉海等[5]研究表明，水力旋流器选取适宜的进料压力有助于分级效率的提高。部分学者采用单因素试验[6]、正交试验[7]的方法进行旋流器分级效率的优化，但正交试验只能找到各因素不同水平之间的最优组合，没有考虑这些因素的交互作用，无法寻求全局最优解。邢雷等[8]、张勇等[9]和LIU等[10]采用响应面法对旋流器结构参数进行优化，构建了出水口含油浓度与旋流器结构参数之间的数学模型，为旋流器分级优化提供了新思路。

本研究基于响应面法，在原有旋流器结构基础上，考察进料浓度、进料压力和旋流器的底流口直径对锂渣除泥效果的影响，从而确立适宜的参数组合方案。研究结果可为锂渣除泥及废弃物资源回收提供有益参考。

1 试验物料及方法

1.1 锂渣粒度组成

通过BT-9300S激光粒度分布仪测得锂渣粒度组成，结果见表1。可以看出，锂渣中细泥含量较高，-20μm细泥含量为34.27%。

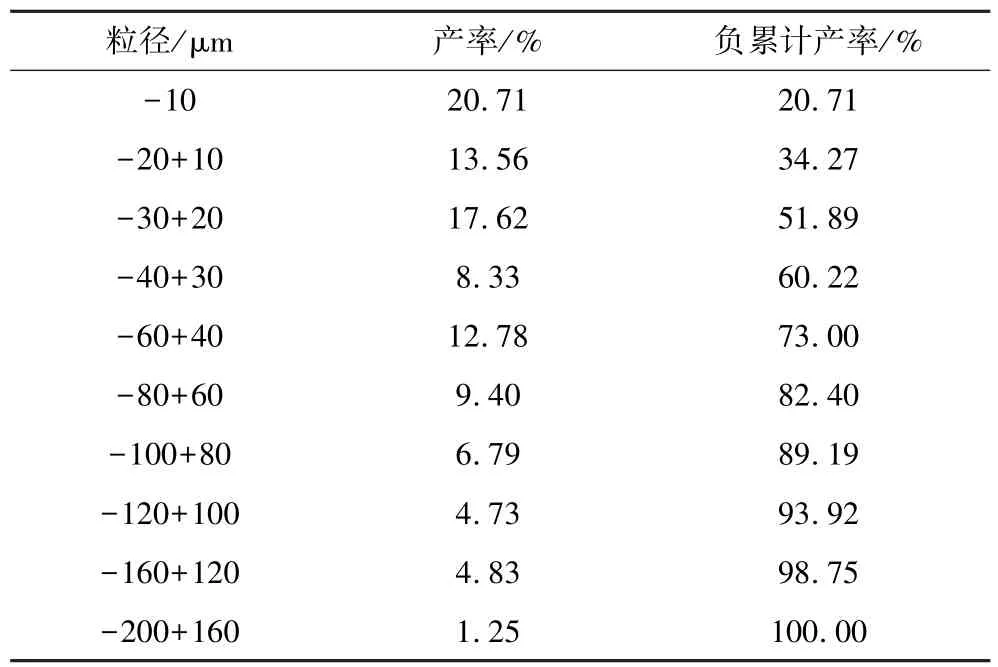
表1 锂渣粒度组成Table 1 Particle size distribution of the lithium slag

1.2 试验方法

试验系统主要由φ50 mm旋流器和给料系统组成。旋流器几何参数见表2，试验系统如图1所示。物料充分混合均匀后，由泵输送到旋流器进行分级，旋流器的底流与溢流经管路返回料筒，保证试验系统循环。通过配置不同浓度的物料、改变进料压力以及更换底流口，接取各试验条件下底流、溢流产物，通过BT-9300S激光粒度分布仪对底流、溢流产物进行粒度分析。

表2 旋流器几何参数Table 2 Hydrocyclone geometry parameters

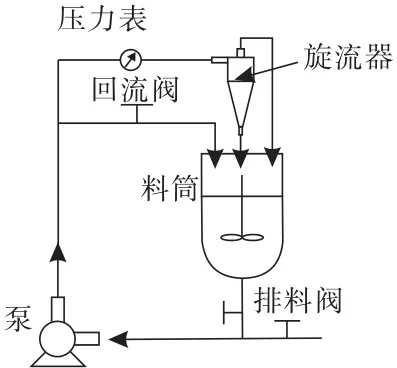
图1 试验装置示意Fig.1 Schematic diagram of experimental device

2 响应面法优化

响应面法是通过对样本空间集合的有限次试验，拟合输出变量的逼近函数来代替真实响应，是一种探究自变量与响应之间关系的一种方法，可以研究2个或者2个以上因素对响应的影响，分析多参数的交互作用，确定各因素对响应的影响程度，用最少的试验次数，确立响应方程[11]。

2.1 响应面法优化原理

回归模型是用不同阶次的多项式来近似表达响应目标和设计变量之间的关系，系统响应Y与设计变量x之间满足[12]:

若采用多项式响应面来近似表示系统设计变量与响应目标两者之间的关系，则有:

式中:β0是偏移项;φi(x)是基函数;βi是基函数系数;k为基函数φi(x)的个数。在实际应用中，可以根据经验来确定响应面模型形式，在设计变量的最优值范围内选用一阶或二阶逼近函数来进行模拟。二阶模型的多项式近似函数为:

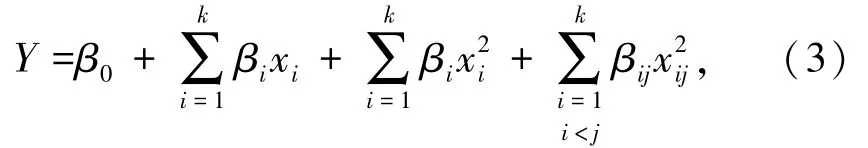
式中:xi为设计变量;k为设计变量数量;β0、βi、βj分别是偏移项、线性偏移和二阶偏移系数;βij是交互作用系数。

一阶逼近函数与二阶逼近函数几乎适合于所有的响应面问题，但一个单一的多项式模型只适合某一区域，并不能在整个变量空间上准确反映真实的函数关系。

2.2 响应面优化设计

本试验运用Box-Behnken Design(BBD)设计方法和Design-Expert 13软件进行设计与分析，研究锂渣进料浓度、进料压力和旋流器底流口直径3个因素对旋流器中-20μm颗粒分级质效率的影响。各因素的水平值与编码值对应情况如表3所示。

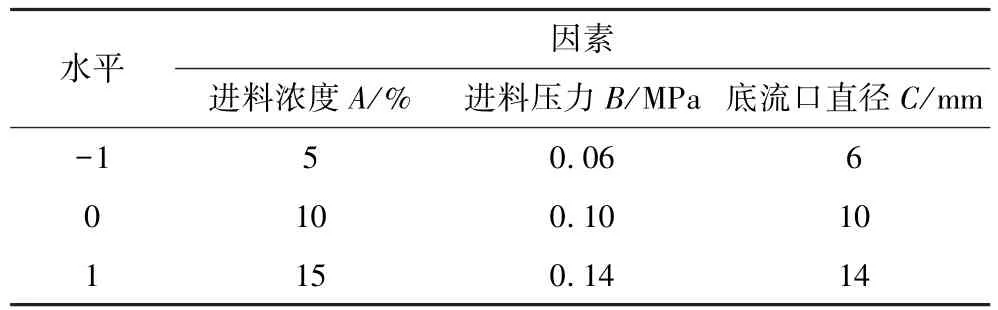
表3 设计因素水平Table 3 Design factor level

3 试验结果与分析

3.1 响应面试验结果

由表3各因素水平，设计生成矩阵试验设计表。该矩阵试验设计表共有17组试验，每个因素都有3水平，为减少误差，中心值重复5次，以-20μm颗粒的分级质效率作为响应值。将试验结果填入表4，对表4数据进行多元二次拟合，得出如下回归方程:

表4 响应面试验设计及结果Table 4 Response face experiment design and results

为判断多元二次回归方程的准确性，基于表4，通过Design-Expert 13对多元二次方程中各项的显著性进行计算分析，结果见表5。P值大小代表各项设计因素的显著性，P值小于0.05即可视为显著[13]。由表5可知，模型P=0.000 1，远小于 0.05，表明该模型试验误差小，具有统计学意义。同时由表5可以看出，自变量一次项B和C显著(P＜0.05)，表明进料压力和底流口直径对-20μm颗粒分级质效率有着明显影响;二次项A2、B2和C2显著，说明浓度、压力以及底流口直径的平方项对分级质效率有着明显影响。失拟项用来表示所用多元二次回归方程与试验拟合的程度，即二者差异的程度。表5中失拟项P值为0.366 0＞0.05，表明无失拟因素存在，可以用该多元二次回归方程替代试验对结果进行分析优化。

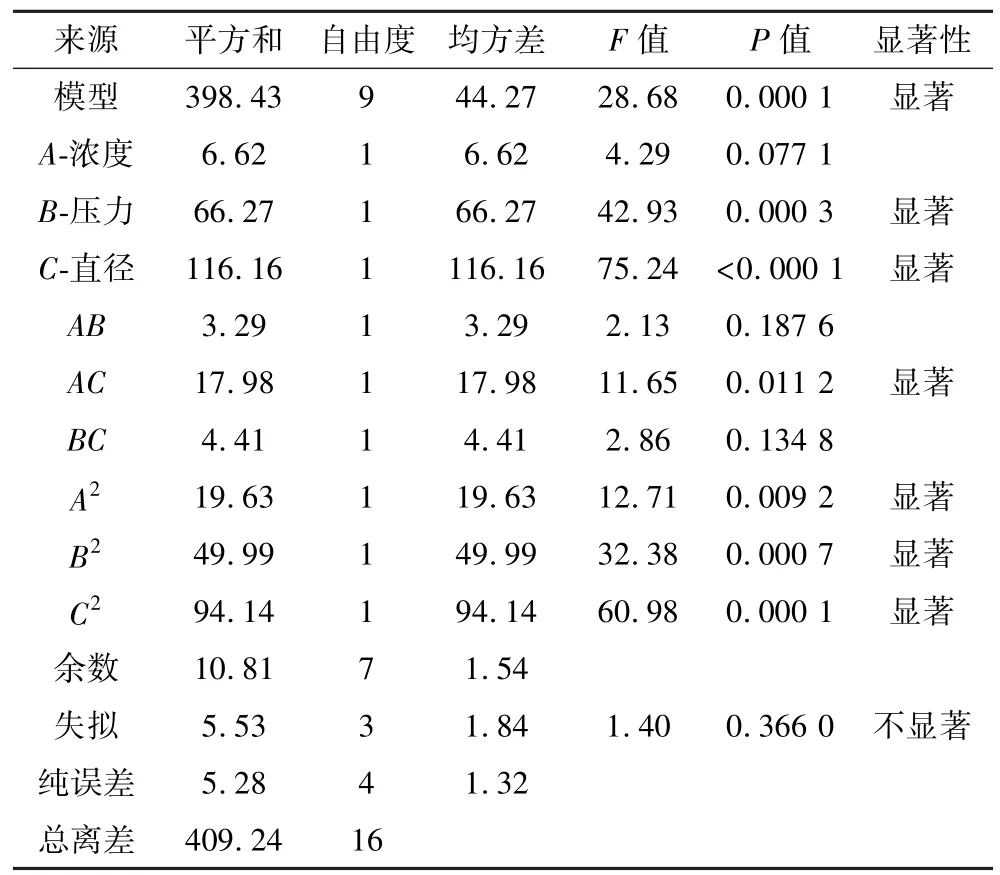
表5 回归方程方差分析Table 5 Analysis of variance of the regression equation

为了进一步验证回归方程的可行性，对拟合方程进行方差分析，结果见表6。多元相关系数R2是反映试验响应值与预测值密切程度的统计指标[14]。从表6可以看出，拟合方程的多元相关系数R2=0.973 6，说明97.36%的响应值变化可以由拟合方程解释。变异系数值为2.02%，小于10%，表示试验的可信度和精度均较高。校正决定系数为0.939 6，大于0.8且与预测多元相关系数的差值小于0.2，说明该模型能充分表示各因素与响应之间的关系。一般情况下，信噪比大于 4，便可以认为模型是合理的[14]。该模型中信噪比为14.551 8，远大于 4，表明该模型合理。基于以上分析，可以说明用该回归方程对试验结果进行分析和预测是可靠的。

表6 回归方程统计误差分析Table 6 Statistical error analysis of the regression equations

图2为实际值与预测值分布图。图2中实际值分布在预测值附近，所建立模型可以较真实地反映实际情况，进一步验证了模型的可靠性。

图2 实际值与预测值分布Fig.2 Distribution of actual and predicted values

3.2 响应曲面优化结果

无论是单因素试验方法还是正交试验方法都无法给出直观的图形来观察其最佳优化点。利用Design-Expert 13给出的多元二次模型，可以做出各因素之间交互作用的双变量三维曲面图。将某一因素固定在中心值上，探究另外2个因素的交互作用以及对分级质效率的影响，结果见图3。

图3 各因素交互作用Fig.3 Interaction of each factor

三维响应曲面的陡峭程度以及等高线的形状可以直观地反映出各因素的交互程度。响应曲面较陡，表明两因素的交互作用较强;响应面曲线较平缓，说明两因素交互作用不明显;等高线呈椭圆形，代表两因素交互作用较强，接近圆形则说明不明显[15-16]。图3(a)响应曲面较平缓，图3(b)等高线接近圆形，说明AB交互作用不明显，并且从图3(b)的等高线可以看出，当进料压力大于0.9 MPa时，-20μm颗粒分级质效率取得较大值;图3(c)响应面较陡，图3(d)等高线呈椭圆形，说明AC交互作用明显，单独增大底流口直径会降低-20μm颗粒分级质效率;图3(e)响应面平缓，图3(f)等高线接近圆形，说明BC交互作用不明显，并且在底流口直径小于11 mm时，随着进料压力的增大，-20μm颗粒分级质效率逐渐增大。

通过Design-Expert 13中的Numerical功能对试验进行优化，得到最佳优化条件为:进料浓度为10.51%，浓度压力0.12 MPa、底流口8.25 mm，此时-20μm颗粒分级质效率最高，为67.95%。以最大分级质效率点为参考点改变3个因素中的1个因素的编码值，得到分级质效率与因素编码值对应关系，结果如图4所示。各因素的斜率陡峭程度表示该因素对输出变量的影响程度，斜率越陡说明影响程度越大。

图4 分级质效率与因素编码值关系Fig.4 Relationship between separation efficiency and factor encoding values

从图4可以看出，在3个因素中，底流口直径(C)斜率最陡，其次是进料压力(B)，最后是进料浓度(A)，说明对分级质效率影响程度从大到小为:底流口直径、进料压力和进料浓度。

3.3 试验验证

设置进料压力为0.12 MPa、底流口直径为 8 mm、进料浓度为10%，进行最优结果的准确性验证。试验结果中-20μm颗粒分级质效率为67.37%，预测值为67.92%，相对误差为0.81%，说明该模型在一定范围内可以有效地优化旋流器分级质效率。优化后底流粒度分布如表7所示，底流-20μm颗粒的含量为5.67%，与进料相比降低了28.6个百分点，锂渣含泥量明显下降。

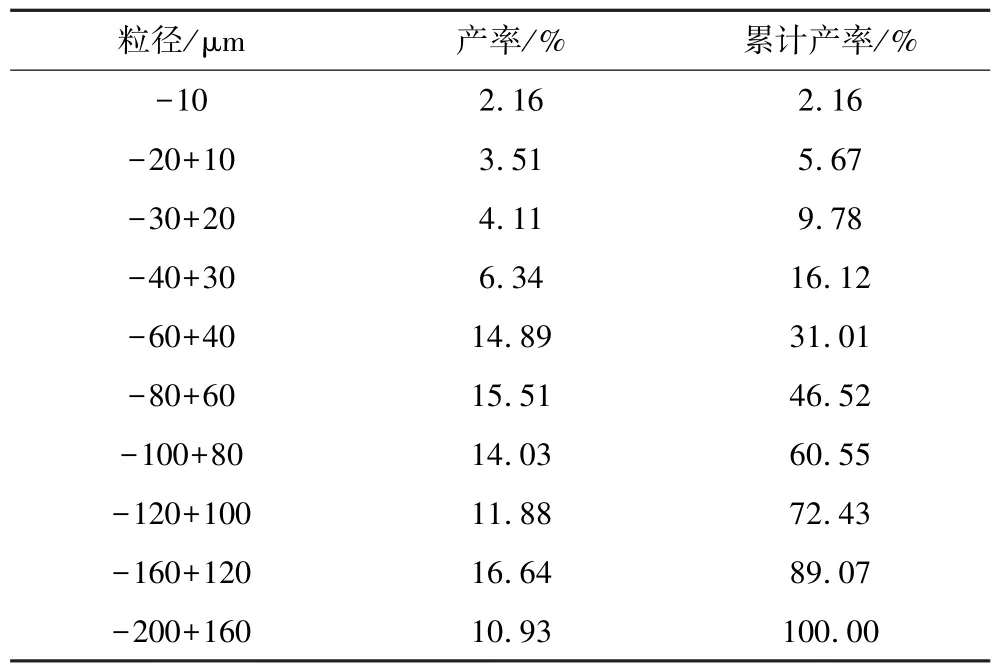
表7 优化后底流粒度分布Table 7 Particle size distribution of the underflow after optimization

4 结 论

(1)采用响应面法可以对旋流器锂渣除泥进行优化设计，对分级质效率进行拟合预测。

(2)基于响应面方法得到了进料压力、进料浓度和底流口直径与-20μm颗粒旋流分级质效率之间的数学模型。进行了优化验证试验，试验结果中-20 μm颗粒分级质效率为67.37%，此时底流中-20μm颗粒的含量为5.67%，与进料相比降低了28.6个百分点，锂渣含泥量明显下降。

(3)响应面研究结果表明对-20μm颗粒分级质效率影响程度从大到小为:底流口直径、进料压力和进料浓度，且进料浓度与底流口直径有着很强的交互作用。