一种固定时间收敛模型参考终端滑模控制方法

张骁骏 袁夏明 王向阳 朱纪洪 李春文

滑模控制方法是一类控制行为不连续的非线性控制方法,通过控制量切换迫使系统状态沿着预定的滑模面运动,具有设计简单、对匹配不确定性和外部扰动鲁棒性强的特点,因而在机器人[1]、飞行器[2]、伺服系统[3]、发电机组[4]等对象中得到了广泛的研究与应用.滑模控制方法设计时首先根据期望系统轨迹选择滑模面,然后设计反馈控制律,使系统轨迹到达并驻留在滑模面上.滑模控制方法的缺点在于其控制律中包含不连续的高频切换项会导致“抖振现象”.针对抖振现象,相关文献提出了基于“边界层”的准滑模动态方法[5]、动态滑模方法[6]、高阶滑模方法[7]等解决方法.

传统的滑模设计方法通常选择线性超平面,收敛速度可以通过参数调节,但只能得到系统状态的渐近收敛特性.终端滑模控制方法(Terminal sliding mode control,TSMC)在超平面设计中引入非线性函数,实现了系统状态的有限时间收敛.Bhat等[8]给出了基于李雅普诺夫函数的有限时间稳定性定理和收敛时间估计.有限时间稳定理论的时间上界与初值有关,学者们进一步研究了具有固定时间上界的固定时间稳定性理论.Polyakov 等研究了基于李雅普诺夫方法[9]和隐李雅普诺夫方法[10]的固定时间稳定性理论,并应用于终端滑模控制器设计[9].标准的终端滑模控制在某些系统状态下会出现奇异问题,限制了其实际应用.Feng等[11]探讨了有限时间非奇异终端滑模面的设计问题,在此基础上,Yang等[12]研究了固定时间收敛非奇异终端滑模面.Zuo等[13]针对二阶非线性系统设计了新型固定时间终端滑模面,并使用了倒立摆模型作为基准测试平台.在此基础上,Li等[14]和Corradini等[15]分别设计新型非奇异终端滑模面,并使用该倒立摆模型进行了测试.Levant等[16]和Andrieu等[17]研究了基于齐次性理论的有限/固定时间收敛理论,并应用于观测器[18]和鲁棒微分器[19]设计.由于其快速收敛性和鲁棒性,固定时间终端滑模控制器在飞行控制[20]、潜航器控制[21]、多智能体控制[22]、电力混沌系统控制[23]、电机无位置控制[24]等方面得到了广泛的应用.

模型参考控制的目标是设计补偿控制器使得被控对象的输出尽可能跟踪参考模型的输出,使广义误差收敛至零[25].补偿控制器用来补偿被控对象与参考模型的状态误差、对象模型不确定性和外部扰动.模型参考自适应[25]基于稳定性理论设计自适应律调节补偿控制器参数.在其基础上,L1 自适应[26]引入低通滤波器使得自适应性能与鲁棒性能解耦,保证闭环系统的鲁棒性和动态性能.除此之外,还可以通过信号补偿方法[27]、神经网络[28]、滑模控制[29]等方法设计补偿控制器.模型参考控制方法将跟踪问题转换为广义误差系统的镇定问题,便于设计系统动态特性,在机械臂控制[30]、飞行控制[31]、混沌系统控制[32]等方面得到了广泛应用.

现有模型参考方法只能得到广义误差渐近收敛的结论,本文将固定时间收敛终端滑模控制方法应用于模型参考方法的反馈控制器设计,使得被控对象状态在固定时间内收敛到参考模型状态.首先,在模型参考控制基础上设计新的控制结构,引入输入限幅和补偿信号滤波,保证补偿信号无损地输入广义误差系统.然后设计了一种新型的固定时间终端滑模面,其可以较好地平衡远离和靠近平衡点收敛速度.在其基础上针对广义误差系统设计终端滑模控制器,使得广义误差信号在固定时间内收敛到零.使用李雅普诺夫方法证明了闭环系统的稳定性并给出了收敛时间上界的估计.最后,将该方法应用于存在极限环的非线性对象控制中,分别针对二阶[33]和三阶[34]对象进行了仿真,并与现有算法进行了比较,验证了该方法的控制效果和鲁棒性.

本文后续内容安排如下:第1 节给出预备知识和定理,并介绍了被控对象;第2 节提出了新的控制器结构和滑模面,针对误差动态设计了固定时间终端滑模控制器,证明了闭环系统的稳定性并得到了收敛时间上界的估计;第3 节采用两种仿真模型进行仿真验证和比较;最后对本文进行了总结.

1 问题描述

1.1 系统模型

考虑如下具有模型不确定性和外部扰动的时变Byrnes-Isidori 标准型系统[35]

其中,x=[x1x2··· xn]T∈Rn为系统状态变量,f(x)为非线性光滑函数,且f(0)=0.Δf(x,t)和d(x,t)分别表示模型不确定性和外部扰动,且存在上界使得|Δf(x,t)|＜D1,|d(x,t)|＜D2.合并表示为等价干扰的形式为dn(x,t)=Δf(x,t)+d(x,t),则有|dn(x,t)|＜D=D1+D2.

参考模型可以表示为

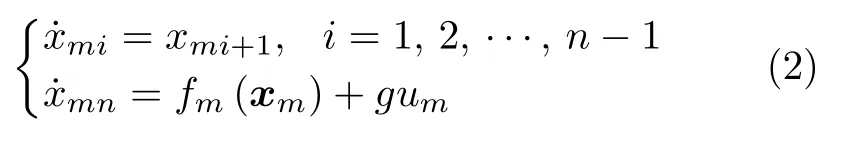
为了方便进行动态特性设计,一般采用线性定常系统,即fm(xm)=[-am1··· -amn]xm.输入um=kgr(t),其中r(t)为指令信号,为参考模型直流增益的逆.本文的控制目标是使系统状态x跟踪参考模型状态xm,从而实现对输入信号r(t)的期望响应.

1.2 固定时间稳定预备知识

Bhat等[8]首先研究了有限时间收敛理论并给出了基于李雅普诺夫函数的判定条件

定义1[8].若系统(1)满足:1)原点是渐近稳定平衡点;2)存在原点的开邻域Dn和正定函数T(x0):Dn→R使得对于所有x0∈Dn{0}有

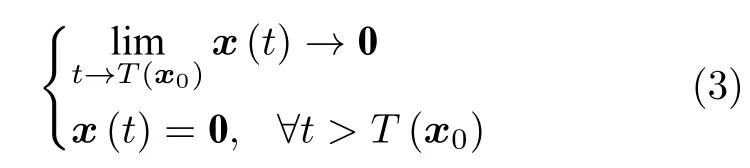
则原点是有限时间稳定的.当Dn=Rn时,原点是全局有限时间稳定的.

定理1[8].若存在连续正定方程V(x):Rn→R满足

其中,参数α,p＞0,p＜1.则系统(1)是全局有限时间稳定的,且收敛时间为T(x0)≤1/(p(1-α))V(x0)1-α.

在有限时间收敛理论的基础上,Polyakov等[9]研究了固定时间收敛理论及其判定条件.

定义2[9].若系统(1)满足:1)原点是全局有限时间稳定平衡点;2)存在一个与初始值无关的收敛时间上界,即存在Tmax＞0使得T(x0)＜Tmax,∀x0∈Rn.则原点是固定时间稳定的.

定理2[9].若存在连续正定方程V(x):Rn→R满足

其中,参数α,β,p,q＞0,p＜1,q＞1,则系统(1)是全局固定时间稳定的,且收敛时间上界为T(x0)＜Tmax=1/(α(1-p))+1/(β(q-1)).

2 控制器设计

2.1 模型参考结构

在传统的模型参考结构的基础上,本文在补偿控制器通道加入低通滤波器,在总输入通道加入限幅,得到如图1 所示的控制器结构.

图1 模型参考控制器结构Fig.1 Structure of the model reference controller proposed

设计被控对象输入u(t)为

其中,sat(u)为限幅函数,限幅值为被控对象输入饱和边界umax,参考输入不会达到饱和边界,引入函数 satn(u)表示施加在补偿信号上的等效限幅函数,uC为固定时间补偿控制器输出.

设计参考模型输入um(t)为

补偿控制量没有达到饱和边界且高频信号弱时,um(t)≈kgr(t).

将式(6)和式(7)分别输入被控对象(1)和参考模型(2),得到系统闭环广义误差信号=xm-x的方程为

对于误差系统,补偿控制量uC不受限幅和滤波的影响,不影响误差状态收敛性;同时通过限幅函数sat(u)和低通滤波器C(u),将超过umax、高频的补偿信号输入到参考模型中,避免输入长时间饱和和高频补偿信号激发被控对象的未建模动态,导致系统不稳定.本文采用固定时间终端滑模方法设计控制量uC,使得广义误差信号在给定时间上界内收敛到原点,则被控对象实现了对参考模型状态的跟踪.

2.2 滑动模态设计

本节提出一种新型终端滑动模态设计方法,该方法受到Corradini等[15]所提出的一类终端滑动模态的启发.

定理3[15].对一类标量系统其中参数β＞0,h(x)为非线性函数,满足h(0)=0,h′(x)≠0,x∈R{0},limx→0(h′(x))-1=0.若原点为全局渐近稳定平衡点,则该系统有限时间稳定,收敛时间为T=|h(x0)|/β.若存在上界Hmax使得|h(x)|＜Hmax,则T＜Hmax/β,系统固定时间收敛.一种典型的非线性函数为

定理3中所述滑动模态的固定时间收敛特性是通过h(x)有界得到的,在系统状态远离平衡点时收敛速度快,但可能导致输入量过大;在靠近平衡点时收敛速度下降,慢于普通终端滑模.与基于定理2 的一般固定时间终端滑动模态sigpx=sign(x)|x|p相比,设计参数较少,不便于平衡不同位置的收敛速度.本文将传统终端滑动模态与定理3 中的滑动模态(9)结合,设计了一种新型终端滑动模态.考虑一类标量系统

其中,参数α,β,p,q＞0,p＜1,选择非线性函数为

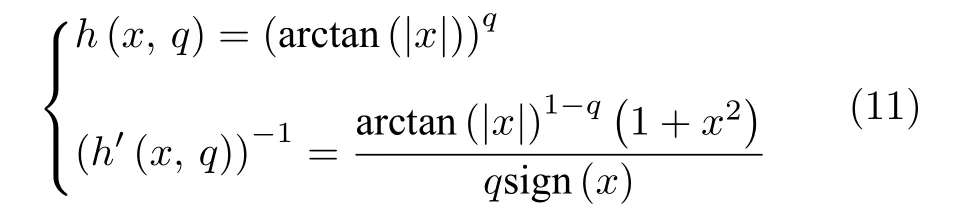
定理4.式(10)所表示的系统固定时间收敛到平衡点,且收敛时间上界为

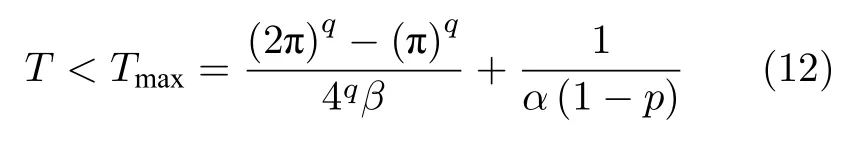
证明.令z=|x|,可得

若z0＞1,设z在T1时刻收敛到z=1,则由式(13)可得

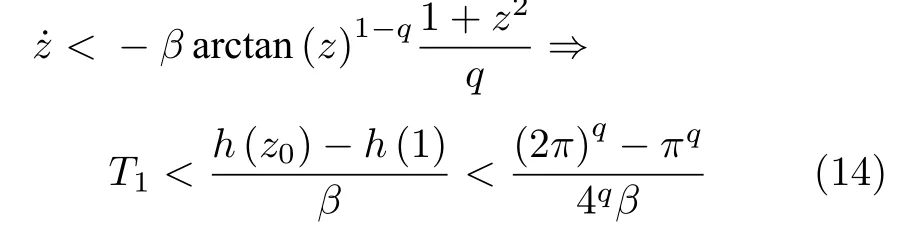
若z0≤1,设z在T2时刻收敛到z=0,则由式(13),可得

z收敛等价于x收敛,则式(10)所表示的系统在固定时间内收敛到原点,且收敛时间上界为

选取不同的参数如表1 所示,考察参数对于标量系统收敛特性的影响.式(10)系统收敛过程如图2所示.

图2 标量系统收敛过程Fig.2 Convergence process of the scalar system

表1 标量系统参数和收敛时间 (s)Table 1 Coefficients and convergence time (s)of the scalar system

参数1 等价于Corradini等[15]采用的方法,对比参数1和参数2 可以看出,本文的增加项提高了标量系统在靠近平衡点区域的收敛速度.以参数2为基准,参数3～6 分别体现了α,β,p,q对标量系统收敛速度的影响:第1 项参数α,p主要影响靠近平衡点区域的收敛速度;第2 项参数β,q主要影响远离平衡点区域的收敛速度;系数α,β对下降速率影响较大,系数越大,收敛越快;指数项p,q影响相对较小.

采用单级倒立摆基准测试模型[13-15]对设计方法进行考察,并与现有方法进行对比[12-15].由于系统收敛时间依赖于参数选择,为便于比较,调整参数使得初始下降速率基本相同.跟踪误差收敛曲线如图3所示.可以看出,本文所提出的滑动模态设计方法的收敛速度优于现有方法,与Corradini等[15]方法相比在靠近平衡点处收敛速度更快.

图3 基准模型跟踪误差曲线Fig.3 Tracking error curve of the benchmark model

2.3 二阶系统控制器设计

首先以二阶系统为例设计控制器,广义误差信号可以表示为

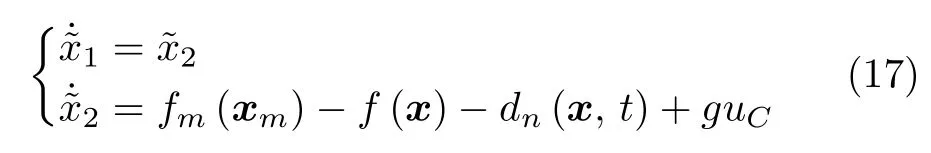
基于式(10)定义滑模变量和趋近律

其中,参数αi,βi,pi,qi＞0,pi＜1,当广义误差信号到达滑模面时,s()=0,则有误差系统按照式(10)的设计滑动模态收敛到原点.

针对式(18)所定义的滑模变量和趋近律,设计非线性控制律(19).其中u1用于抵消误差动态,u2为滑模运动控制项,u3为趋近运动控制项.

定理5.采用式(19)所述非线性控制律的二阶广义误差系统固定时间稳定,且收敛时间上界为

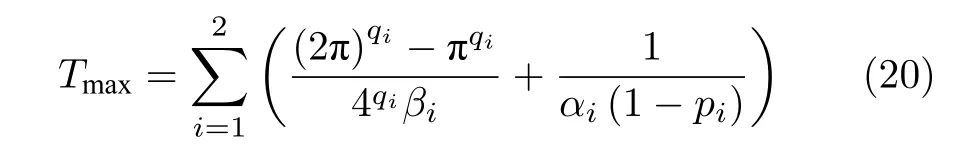
证明.将输入式(19)代入式(17),得到滑模变量的导数如式(21)所示.

则误差系统全局渐近稳定,s最终收敛到0.又由式(21)和定理4,可得系统趋近滑模面的到达时间为

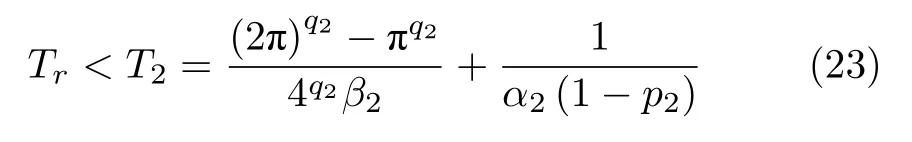
系统到达滑模面后s=0,随后沿着滑模面收敛到原点,由式(18)和定理4 可得收敛时间为

综上所述,系统在固定时间内收敛到原点,收敛时间上界为误差系统的相平面图如图4 所示.

图4 误差系统相平面图Fig.4 Phase plane plots of error dynamic

相轨迹穿过S3后沿着预定轨迹运动,不会再次进入奇异区,因此,系统仍然是固定时间稳定的,收敛时间上界为

系统动态到达滑模面后,控制量中的不连续项可能会导致抖振问题,引入连续函数(29)近似切换函数以减少抖振影响,参数ρ越大越接近切换函数.

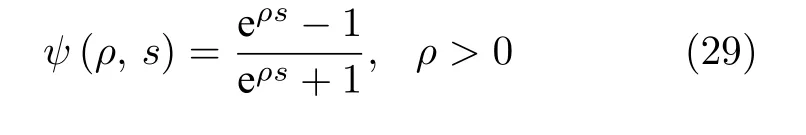
2.4 高阶系统控制器设计

高阶系统广义误差信号可以表示为

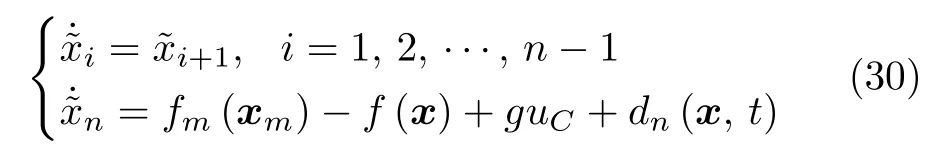
由于第2.2 节所述终端滑动模态适用于相对阶为1 的系统,因此高阶系统需要设计具有递归结构的滑动模态

其中,参数αi,βi,pi,qi＞0,pi＜1.将误差动态代入式(31),得到滑模变量sn-1的导数如式(32)所示

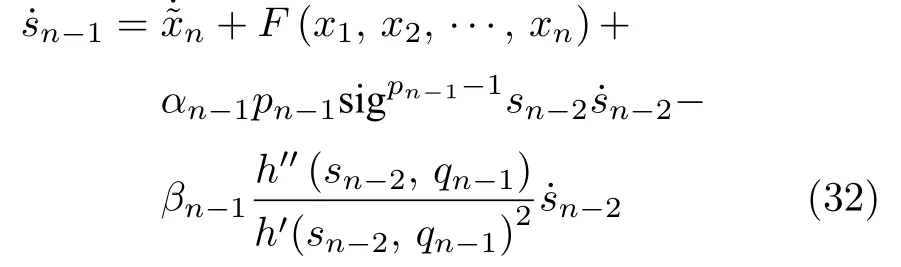
将其代入式(32),可得滑模变量sn-1的导数为

则闭环系统渐近稳定,各阶滑模变量依次收敛,收敛时间上界为

3 仿真验证

3.1 二阶翼摇模型验证

翼摇是大后掠角飞机在大迎角时出现的一种滚转通道自激振荡的现象.Capello等[33]通过风洞实验建立了两种飞机机型的翼摇运动模型,并使用L1 自适应算法实现了对于该现象的抑制.在此基础上,学者们使用基于扩张状态观测器的鲁棒控制[36]、自适应控制[37]等方法对该模型进行研究.

翼摇运动模型可以表示为

两种机型的模型参数如表2和表3 所示[33].

表2 模型A 的气动数据Table 2 Aerodynamic coefficients for Model A

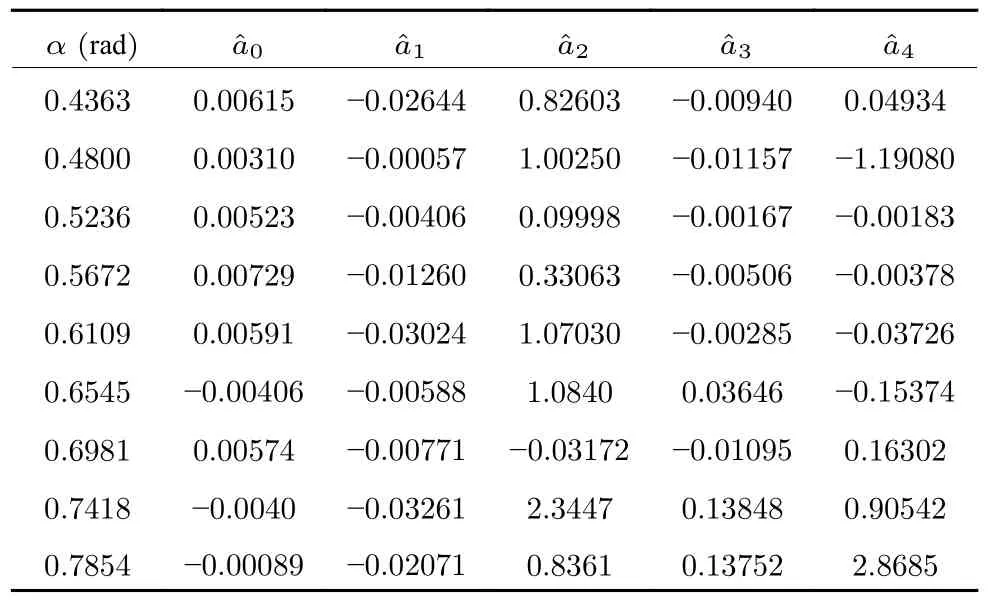
表3 模型C 的气动数据Table 3 Aerodynamic coefficients for Model C

迎角αAOA=0.57 时的模型C 开环响应相平面如图5 所示,系统开环响应存在极限环.

图5 模型C 开环响应极限环Fig.5 Open-loop response of Model C exhibiting limit cycle

参考模型选择为

采用第2.1 节所述控制结构,则广义误差信号可以表示为

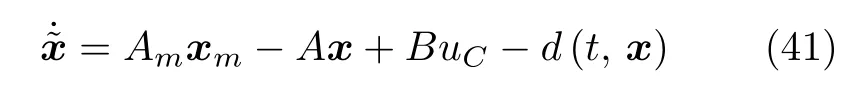
采用第2.3 节所述方法设计固定时间收敛终端滑模控制器为

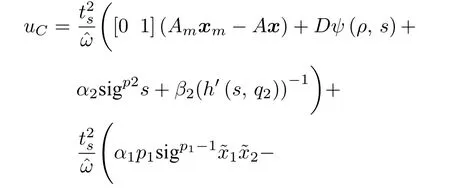
选取控制器参数为α1=α2=3,β1=β2=1,p1=q1=5/9,p2=q2=3/9,收敛时间估计为Tmax=1.9 s.

外部扰动dˆ(t,ϕ(t),ϕ′(t))=10 sin(2πt)+20 sin(πt)+w,w为白噪声.采用simulink 搭建模型,龙格库塔方法进行仿真,步长为0.0001 s.分别仿真不同初始滚转角收敛特性、不同迎角情况下的滚转角收敛特性和对阶跃信号的跟踪.采用绘制输入曲线.

1)使用模型A 测试不同初始滚转角下控制器的收敛性能.固定迎角αAOA=0.61,初始滚转角选择为ϕ0=-1.22,-0.52,-0.26,0.26,0.52,1.22.参考信号恒为零,得到仿真结果如图6 所示.

图6 不同初值模型A 闭环响应Fig.6 Closed-loop response of Model A for several initial

可以看出,控制器(42)可以实现对不同初始角度的镇定.随着初值增加,收敛时间增加不大,在0.4 s以内,远小于估计上界,体现了控制器的固定时间收敛特性.

2)使用模型C 测试不同状态下控制器的鲁棒性,以迎角αAOAm=0.61 时的模型参数作为已知模型,初始滚转角ϕ0=0.35,初始迎角分别设置为αAOA0=0.48,0.57,0.65,0.74.实际仿真迎角在已知迎角附近变化,取αAOA=αAOA0+0.044 sin(2t).仿真结果如图7所示,不同迎角下滚转角误差响应(图7(a))几乎相同,输入(图7(b))补偿了不同迎角下的模型误差和扰动,体现了控制器对于模型不确定性和外部扰动的鲁棒性.

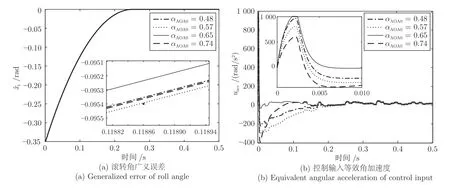
图7 不同迎角模型C 闭环响应Fig.7 Closed-loop response of Model C for several angle of attack

3)使用模型A 考察控制器对阶跃信号的跟踪性能.并与现有的模型参考类方法(L1 自适应[26],信号补偿[27])和基于现有非奇异固定时间终端滑模面(Corradini等[15],Li等[14],Yang等[12])的模型参考方法进行比较.以αAOAm=0.61 时的模型参数作为已知模型,初始滚转角ϕ0=0.70,实际仿真迎角为αAOA=(0.61+ 0.087 sin(2t)).仿真结果如图8 所示.从仿真结果可以看出,本文所采用的控制器收敛时间最短,可以一直保持较快的下降速度,并且初始阶段输入量较小,没有达到饱和边界.文献[15]和文献[14]所设计的滑模面在初始阶段下降较快,但误差接近原点时收敛速度减缓;文献[12]和L1自适应[26]整体收敛速度较慢;信号补偿[27]方法收敛速度较快,但会出现误差超调,整体收敛时间慢于本文算法.

图8 模型A 对阶跃信号跟踪响应Fig.8 Closed-loop response to step signal tracking of Model A

3.2 三阶模型验证

采用文献[34]所用的3 阶非线性模型进行验证,被控对象如式(43)所示

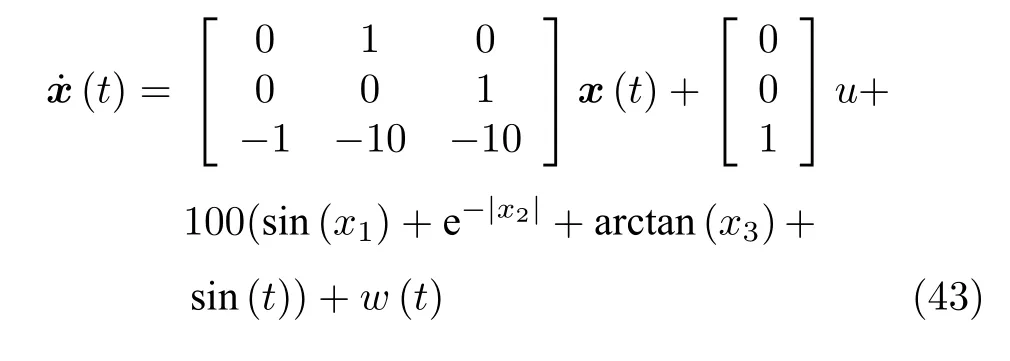
其开环特性如图9 所示,存在三维空间极限环.选取参考模型参数 [-1-2.414-2.414].广义误差信号表示为

图9 模型(43)开环响应特性Fig.9 Open-loop response of model (43)

选取控制器参数为α=[0.8 2.1 2.1],β=[0.04 0.4 0.4],p=[7/9 5/9 5/9],q=[5/9 4/9 4/9],收敛时间上界估计为Tmax=19.7 s,初始状态x0=[4-2-1]T.文献[15]方法参数为[0.12 0.55 0.6].

图10 为期望输入为阶跃信号时的仿真结果.从仿真结果可以看出,本文算法可以一直保持较快的下降速度,收敛时间T=2.8 s.从输入曲线可以看出,基于文献[15]终端滑模面所设计的控制器在收敛时间相近的情况下,初始输入较大,达到了限幅值,因此导致补偿信号输入参考模型中,使得参考模型状态向被控对象实际状态逼近.虽然导致最终跟踪期望输入r(t)较慢,但保证了广义误差信号收敛速度不变,避免了长时间饱和可能导致的系统不稳定,体现了本文所采用的控制结构的优势.信号补偿算法[27]和L1 自适应[26]的特性与二阶系统仿真结果基本相同.

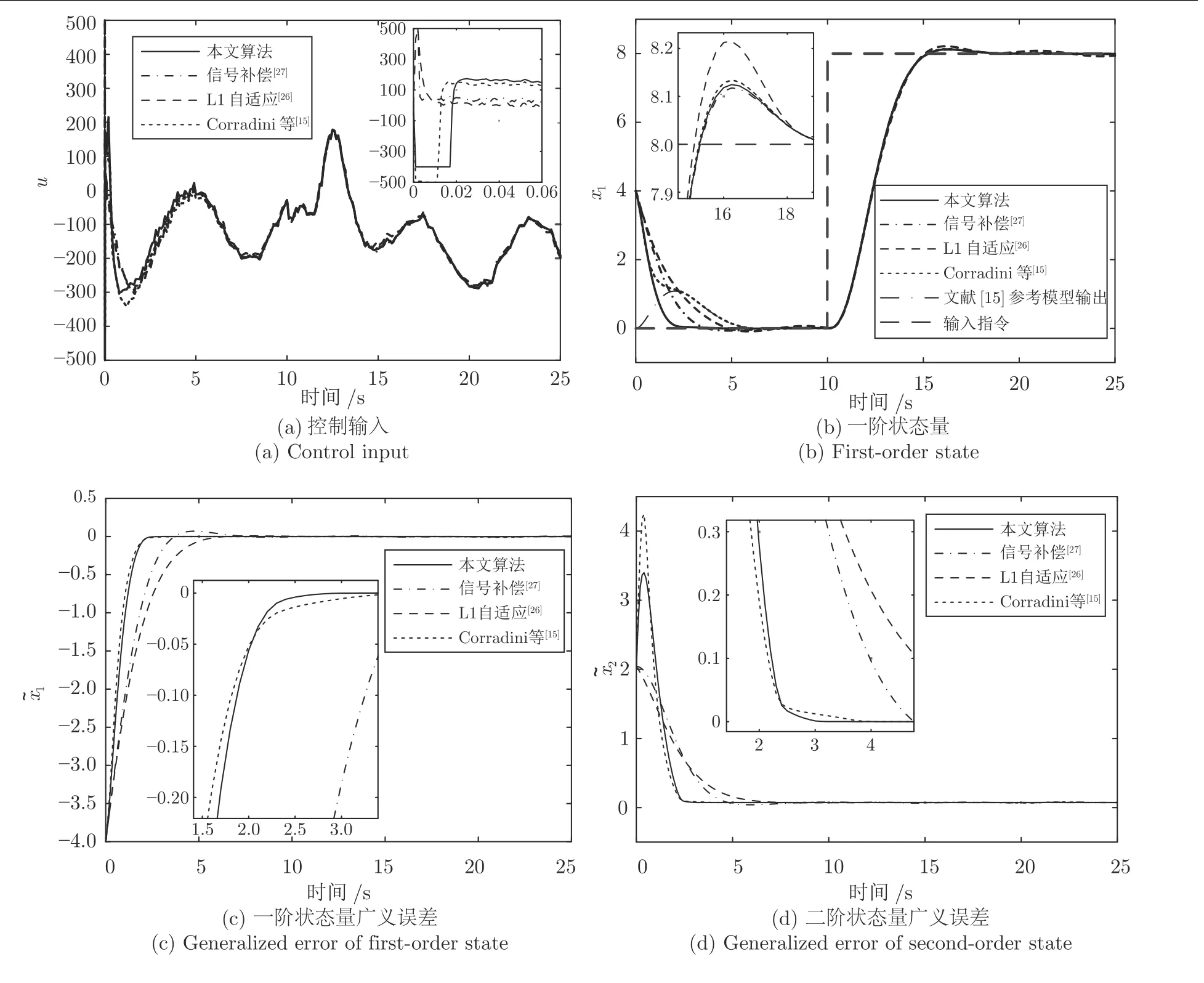
图10 闭环系统对阶跃信号跟踪响应Fig.10 Response to step signal tracking of closed-loop system

综上所述,本文所采用的控制结构可以避免长时间饱和和高频补偿信号输入被控对象,引起系统不稳定;所设计的终端滑模面在整个下降过程中可以保持较快的下降速度,较好地平衡了远离平衡点处和靠近平衡点处的收敛特性,避免了初始状态误差较大时补偿输入过大;可以保证被控对象的状态在固定时间内跟踪参考模型状态.

4 结束语

本文针对存在模型不确定性和外部扰动的时变非线性系统研究了固定时间终端滑模模型参考控制方法:1)设计了新型模型参考控制结构,在加入输入限幅和补偿信号滤波的同时,保证了广义误差系统收敛特性;2)设计了新型终端滑模面,较好地平衡了远离平衡点和靠近平衡点的收敛特性;3)针对高阶系统设计了递归结构终端滑模控制器.本文控制器保证了误差动态在固定时间内收敛到原点,使得被控对象能够在固定时间内收敛并跟踪参考模型动态,便于进行闭环系统动态设计.后续工作考虑采用自适应算法或扰动观测器动态调整切换项增益以减少控制量抖振,考虑结合鲁棒微分器和反步法设计高阶系统控制器,避免解析求解导致高阶系统控制器过于复杂.