基于Green 函数法的太阳高能粒子行星际扩散过程模拟*

朱琳玲 张效信 顾斌

1(中国气象局空间天气重点开放实验室/国家卫星气象中心(国家空间天气监测预警中心) 北京 100081)

2(许健民气象卫星创新中心 北京 100081)

3(南京信息工程大学物理系 南京 210044)

4(南京信息工程大学空间天气研究所 南京 210044)

0 引言

当太阳活动比较剧烈，出现耀斑爆发或者日冕物质抛射时，常常喷射出大量高能带电粒子（Solar Energetic Particle，SEP），包括质子、电子、α 粒子以及其他一些重离子。耀斑爆发或日冕物质抛射后一段时间，在地球轨道附近可观测到高能粒子的强度突然增加，即SEP 事件。由于从太阳喷射出来的高能粒子绝大部分都是质子，占高能粒子总数的90%以上，所以SEP 事件也称作太阳质子事件，质子的能量范围通常在10～100 MeV 之间[1]。一次SEP 事件通常经由两种加速过程产生，分别为日冕加速过程和行星际激波加速过程。研究认为：在日冕加速过程占主导的情况下，产生的主要为持续时间约几个小时的脉冲型SEP 事件；在行星际激波加速过程占主导的情况下，产生的主要为持续时间约为数天的缓变型SEP 事件[2,3]。由于SEP 事件的持续时间较长，其对空间飞行器以及宇航员能够造成极大的危害，同时SEP 事件发生通常与太阳活动区存在非常密切的关系[4]，因此SEP 事件的产生及其在行星际中的扩散过程是空间天气研究的主要内容之一[5-9]。

在发现行星际螺旋场之前，没有理论能够解释观测到的SEP 事件通量结果。尽管之后Reid等[10]和Axford[11]在研究中考虑到了行星际螺旋场，不过其模拟结果与观测结果存在较大的差异。通过人为设置吸收条件，Burlaga等[12]利用各向异性传输模型计算得到了与观测结果近似的模拟结果，但是在实际宇宙空间中并不存在任何吸收边界。Parker等[13]认为宇宙射线实际上就是带电粒子在非均匀行星际磁场中的随机运动，在此基础上提出了粒子分布函数和运动方程，为后续研究SEP 事件提供了非常好的条件。由于很难通过解析法求解这些方程，在早期的研究中通常采用有限差分法或有限元法进行求解[14,15]，不过这些方法存在一些问题，即对于高纬度区域SEP 事件计算量庞大，计算不稳定。此外，也有学者利用随机微分方程法来研究SEP 事件的传输过程[16,17]。

为了能够更加便捷准确地模拟SEP 事件，基于Green 函数的传播方程半解析解被广泛应用。Huang等[18-20]提出了一种SEP 事件模型，该模型同时考虑了SEP 事件源在日冕区和行星际中的扩散过程，另外基于Green 函数方法来求解传输过程，模拟结果与观测结果非常一致。Huang等[19]提出的模型将SEP事件在日地之间的传播过程简化为包含若干特征参数的传输方程，包括与SEP 在日冕中横向传播物理过程相关的日冕扩散区的扩散系数，SEP 在日冕中传输时逃逸到行星际介质的逃逸时间，SEP 在行星际空间中沿磁力线方向的径向扩散系数等，对于理解整个传输过程有着显著的优势。Wang等[21]利用上述模型计算了同一次SEP 事件中不同卫星观测到的通量变化过程，不过对于该模型中的各项参数是如何影响SEP 事件的行星际扩散过程，以及影响程度如何，目前尚未明确。本文拟利用文献[19]提出的模型针对不同类型的SEP 事件进行模拟，探讨不同模型参数对于SEP 事件的影响机制，并将各个参数与太阳活动爆发的时空特征和粒子扩散行为相互联系，为近地空间SEP 事件的预测提供理论支撑。

1 数据与模型

1.1 数据来源

研究所用数据主要包括由美国国家海洋和大气管理局（NOAA）GOES 系列卫星所观测到的SEP 事件数据以及由美国国家航空航天局（NASA）ACE 卫星所观测到的太阳风速数据，所有数据均可以从日本空间科学研究所（ISAS）创建的多学科数据归档和传输系统（DARTS）网站*http://www.darts.isas.jaxa.jp下载，该网站主要针对天体物理学、太阳物理学、太阳–地球物理学、月球和行星科学等领域空间科学任务获得的数据进行归档，并提供数据服务。此外，NOAA 空间环境服务中心网站**https://umbra.nascom.nasa.gov/SEP给出了自1976年以来记录到的主要SEP 事件，并可查询事件相应的日冕足点、耀斑等级等参数。由于该网站所统计的SEP 事件仅更新至2017年底，因此本文分析和模拟的数据均选取自1976－2017年时间范围内。

1.2 SEP 两相传输模型

已有研究表明，SEP 存在很大的日冕横向分布，因此不能将SEP 脉冲点源用作初始条件，而应为与时间有关的粒子日冕横向分布发射源。图1 给出了SEP日冕扩散和行星际传输示意图。假设SEP 产生在A点，并在日冕内部传播形成随时间不断扩大的粒子分布区域（图1中B至C的弧段），同时该区域粒子不断向行星际空间逃逸，因此该区域可视为一个不断产生SEP 的时空分布源。由于太阳的自转，行星际大尺度磁场的磁力线是Archimedes 螺旋线，其中经过SEP 产生位置的一条磁力线称为最佳磁连接，即图中A至F的磁力线。假设地球的位置在E点，D至E为经过地球的磁力线，由于受到大尺度磁场的束缚，粒子在行星际空间的横向扩散相比沿磁力线方向的径向扩散要小得多，所以SEP 爆发位置离D点越近，被地球卫星观测得到的粒子强度越大，而D点一般位于西经50°左右。

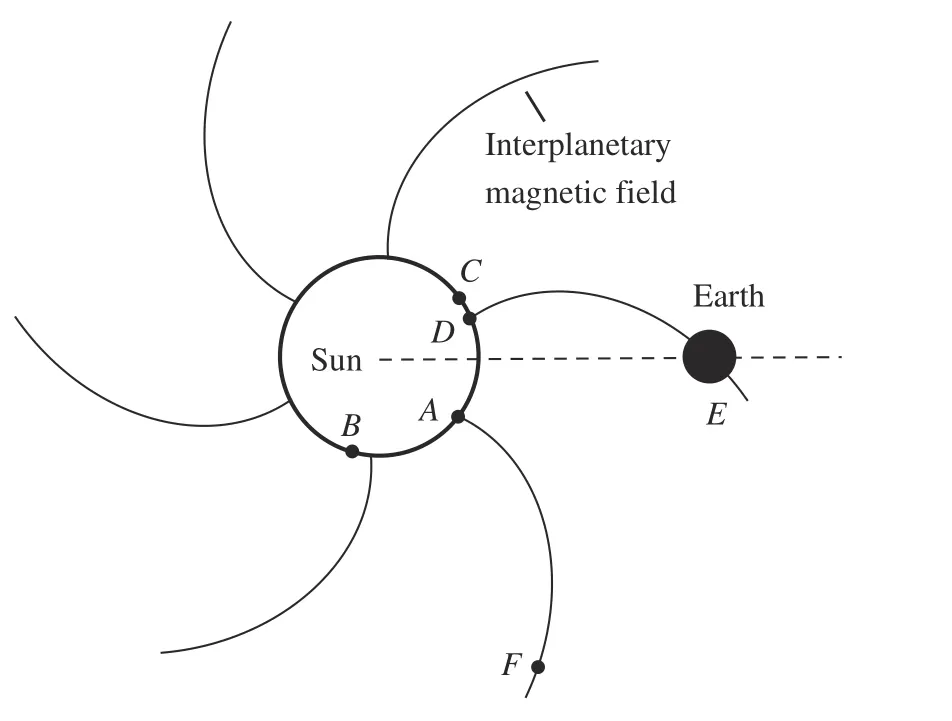
图1 SEP日冕扩散和行星际传输Fig.1 Two-phase propagation scheme of SEPs from solar surface to interplanetary area

1.3 SEP日冕分布与行星际传播方程

SEP 在日冕内部横向传播，并形成随时间不断扩大的日冕分布源。在柱坐标下，假定日冕横向传播是各向同性的，则距离粒子产生位置的经度间隔θ处的SEP 密度f0(r,θ,z,t)可近似为

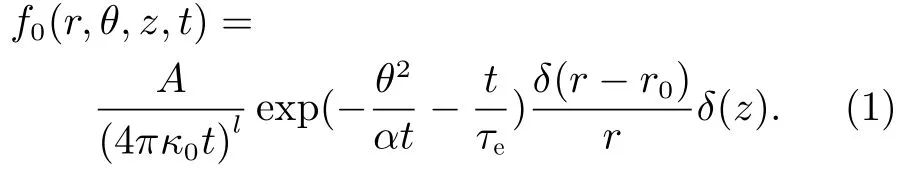
其中，A和l为常数，r0为太阳半径，τe为逃逸时间，κ0为日冕区扩散系数，α=κ0/r02，函数中自变量r为分布源距离太阳中心的距离，θ为分布源距离粒子产生位置的经度间隔，z为分布源在垂直黄道面的高度坐标，t为传播时间。

从日冕中逃逸之后，SEP 会在行星际进行传播，根据文献[19]等的研究，在假定扩散系数与行星际空间位置无关的情况下，SEP 在行星际介质中的传播可以用下列有源方程来近似描述：

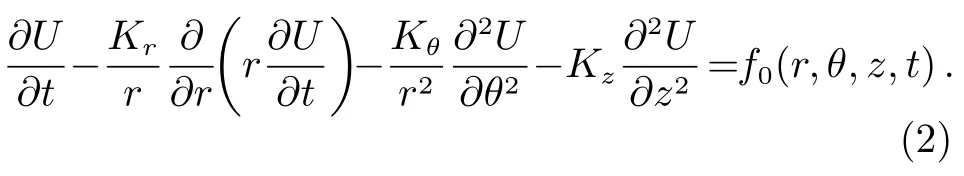
其中，函数U为行星际空间的SEP 分布密度，Kr为行星际径向扩散系数，Kθ为行星际横向扩散系数，Kz为垂直黄道面的扩散系数。

式（2）的解可通过求解其Green 函数得到，推导过程详见文献[19]，最后求得Green 函数的如下表达式：

2 分析与结果

2.1 一次SEP 事件模拟结果及日冕足点的经度统计分布

在SEP 的行星际传播方程中，磁力线日冕足点的经度值为其中的一个重要参数。对于处于最佳磁连接的磁力线，其经度一般处于西经50°，不过受日冕内部传播的作用影响，通常发生在最佳磁连接日冕足点东西各50°范围内，即0°W－100°W 之间的SEP事件均能够被卫星观测到[18]。依据NOAA 空间环境服务中心公布的数据，本文统计了自1976－2017年期间记录到的217 次SEP 事件的日冕足点经度，统计结果如图2 所示，其中西经用正值表示，东经用负值表示。从图2 可以发现，发生在0°W－100°W 范围内的SEP 事件共有143 次，占到事件总数的约65.9%，该统计结果很好地体现了SEP 事件日冕横向分布的东西效应。

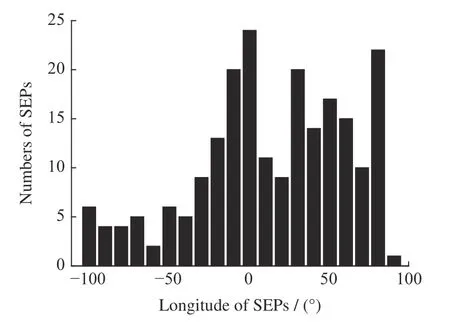
图2 1976－2017年观测到的SEP 事件日冕足点经度位置统计Fig.2 Statistical histogram of coronal-foot-point longitude of 217 SEP events from 1976 to 2017

采用上文中介绍的SEP 两相传输模型，按照文献[19] 提出的Green 函数法，首先针对发生在2005年6月16日的一次SEP 事件进行二维粒子通量模拟，即不考虑事件在垂直黄道面的扩散过程（物理量在z方向的变化为零，或者是常量）。此次事件发生在87°W，处于最佳磁力线日冕足点偏西的位置。图3给出了此次SEP 事件中GOES 卫星观测到的质子能量大于10 MeV 的通量结果（图3 a 黑色实线）以及期间ACE 卫星观测到的太阳风速（图3 b），从图3 可以看出，此次SEP 事件强度幅值约为43 cm–2·s–1·sr–1，期间的太阳风平均速度vsw约为583 km·s–1。通过反复试验计算得到了此次SEP 事件的模拟结果（图3 a黑色虚线），与观测结果（图3 a 黑色实线）相比，两者具有非常好的一致性。在本次模拟中，日冕区扩散系数κ0取值为4.0×1015cm2·s–1，行星际径向扩散系数Kr取值为1.0×1021cm2·s–1，逃逸时间τe取值为1000 s。由于受到大尺度磁场的束缚，粒子在行星际空间的横向扩散相比沿磁力线方向的径向扩散要小得多，因此在模拟计算中，行星际横向扩散系数Kθ通常取行星际径向扩散系数Kr的0.04倍[18]。通过对该事件的数值模拟，能够得到较为可靠的粒子沿日冕区和在行星际中的传输参数，有助于更好地认识和理解SEP 的传输过程。

图3 2005年6月16日SEP 事件观测与模拟结果对比（a）及期间的太阳风速（b）Fig.3 Comparison between the measurement and the simulation of the SEP event observed on 16 June 2005(a) and the associated solar wind velocity (b)

2.2 不同参数对于SEP 事件的影响

为了明确模拟计算所用的不同参量，包括日冕区扩散系数κ0，行星际径向扩散系数Kr，行星际横向扩散系数Kθ，逃逸时间τe，以及SEP 发生位置、太阳风速vsw等对于SEP 事件扩散和传播过程的影响，并探讨其中的物理意义，有必要针对各个参数进行敏感性分析，即在只改变其中一个参数的基础上研究各个参数对于模拟结果的影响。以图3 中模拟得到的2005年6月16日SEP 事件为参考组（Reference），在敏感性试验组中，除了将SEP 发生经度设置在最佳磁力线日冕足点（50°W）外，其余参数的变化设置为参考组的两倍。试验组（Test）的具体参数设置如表1所示，其中试验组三（Test 3）为试验组二的对比试验，相对于参考组改变了发生位置和太阳风速vsw两个参数，而相对于试验组一仅改变了太阳风速vsw一个参数。需要说明的是，试验组二和试验组三中用到的太阳风速（1166 km·s–1）已明显超过实际能够观测到的正常太阳风速，其目的主要是为了显著地呈现出太阳风速改变对于SEP 事件通量的影响。

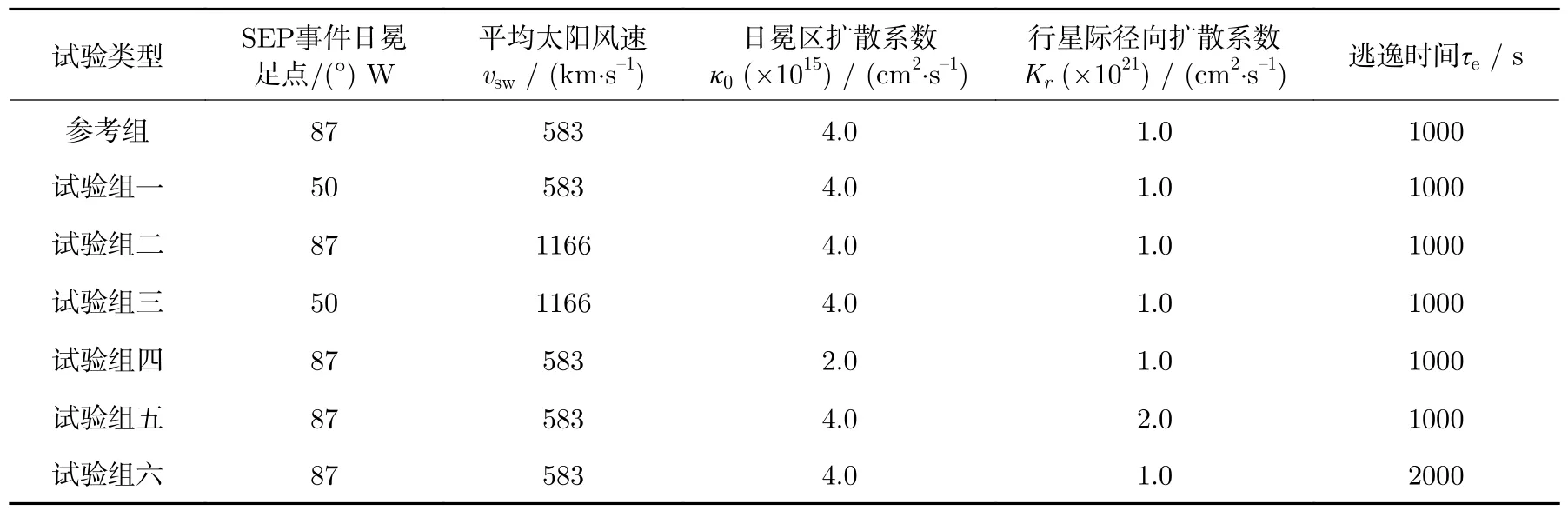
表1 不同参数对于SEP 事件影响的敏感性试验参数设置Table 1 Parameter setting of sensitivity test for SEP events

图4 给出了参考组和试验组的模拟结果，其中红色曲线为参考组模拟结果。首先探讨改变日冕足点和太阳风速时对SEP 事件产生的影响，对比参考组和试验组的模拟结果可以发现，当仅仅改变发生SEP 事件的日冕足点经度位置时（图4 中Test 1），将影响卫星探测到此次事件的探测时间和峰值，由于处于最佳磁力线日冕足点的SEP 事件无需经过日冕区的横向扩散过程，直接经过最佳的行星际大尺度磁场磁力线即可传输至地球，所以实际发生SEP 事件的位置越靠近最佳磁力线日冕足点，卫星越能及早探测到该事件，同时由于质子没有经过日冕区扩散消耗，探测到的SEP 事件峰值也越大。行星际大尺度磁场与太阳风关系密切，其由太阳风携带等离子体流至行星际空间后形成，太阳的自转进一步使得行星际磁力线被扭曲成螺旋结构，因此太阳风速度的大小会直接影响日地行星际磁场的结构。对于发生在非最佳磁力线日冕足点的SEP 事件而言，当太阳风速vsw增大到参考组的两倍时（图4 中Test 2），模拟得到SEP事件峰值出现明显的下降，可能原因在于较强的太阳风使得SEP 事件更快地扩散至行星际空间，使得粒子无法有效地传输至最佳磁力线日冕足点。为了验证这个推测，增加了针对试验组二的对比试验，将SEP 事件发生位置设置在最佳磁力线日冕足点，模拟太阳风速vsw增大两倍前后的结果，对比结果如图4中的Test 1 和Test 3 曲线所示，可以发现当SEP 事件发生在最佳磁力线日冕足点时，太阳风速增大能够使得模拟结果幅值增大，即更加有利于该事件向地球扩散，即不同位置处的SEP 事件受太阳风速的影响的机制是不同的。

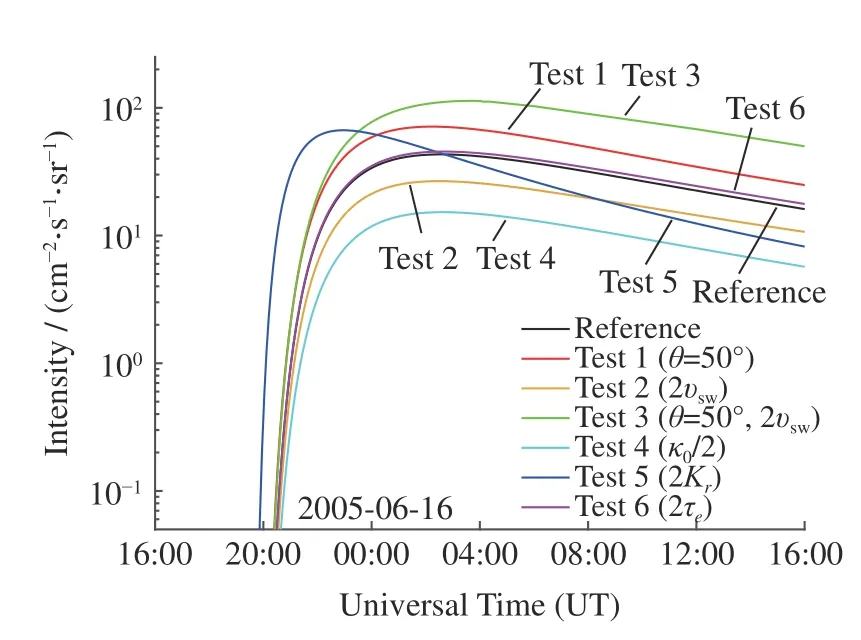
图4 两相模型不同参数的敏感性试验结果Fig.4 Sensitivity test results of different parameters of the two-phase model

在SEP 事件中，粒子的扩散过程与近地面观测到的通量密切相关。当日冕区扩散系数κ0减小到参考组的1/2 时（图4 中Test 4），模拟结果的峰值变小，同时该事件的发生时间也明显滞后。分析认为，由于κ0与SEP 在日冕区的扩散过程相关，κ0减小后日冕区粒子扩散到最佳磁力线日冕足点的时间延长，相应地粒子在日冕扩散期间损耗的粒子数也更多。与其他参数相比，星际径向扩散系数Kr的改变对于模拟结果的影响主要体现在峰值到达时间上（图4 中Test 5），这是因为在SEP 两相传输模型中粒子主要是在大尺度的行星际磁场中传播，日冕横向传播过程相对较短，Kr越大粒子到达近地面观测点的时间也越短，同时传播过程中行星际横向扩散造成的粒子数损耗也更少，这样就使得更大的Kr值对应更高的SEP事件幅值和更短的峰值到达时间。在SEP 事件中，粒子源的释放时间决定了该事件的持续时间，而逃逸时间τe就是表征粒子源释放时间的物理量，模拟结果显示仅仅改变逃逸时间τe主要影响SEP 事件的持续时间（图4 中Test 6），不过在模拟中可以发现，逃逸时间τe相对其他物理参量而言，其对于SEP 事件模拟结果的影响是最小的。

2.3 发生在不同日冕足点SEP 事件的模拟对比

综上模拟了一次发生在最佳磁力线日冕足点偏西（87°W）的SEP 事件，为了验证该模型的有效性，选取另外三次SEP 事件进行模拟。其中，图5(a)为一次发生在2017年9月4日的SEP 事件观测和模拟结果。该次事件日冕足点位于最佳磁力线日冕足点偏东（16°W）的位置，期间记录的太阳风速在一段时间内缺失（见图5 b），仅计算后半部分太阳风速的平均值，约为520 km·s–1，日冕区扩散系数κ0取值为1.0×1015cm2·s–1，行星际径向扩散系数Kr取值为4.0×1020cm2·s–1；图5(c) 和图5(e) 为发生在SEP 事件日冕横向分布的东西效应之外的两次事件的观测和模拟结果。为了增大研究对象的差异性，选取的日冕足点分别位于12°E 和82°E，事件发生时间分别为2013年4月11日和2014年2月25日，平均太阳风速约为440 km·s–1（见图5 d）和447 km·s–1（见图5 f），日冕区扩散系数κ0取值分别为8.0×1014cm2·s–1和1.3×1015cm2·s–1，行星际径向扩散系数Kr取值分别为5.0×1020cm2·s–1和2.2×1020cm2·s–1。模拟结果与观测结果均具有非常好的一致性，表明本文所用的模型能够较好地模拟发生在不同日冕足点的SEP事件。

图5 三次SEP 事件观测和模拟结果对比以及事件期间的太阳风速观测结果Fig.5 Comparisons between the measurement and the simulation of three SEP events and their associated solar wind velocities

为了对比发生在不同日冕足点下的SEP 事件特征，表2 给出了本文所模拟的4 次SEP事件的特征参数。从表2 可以发现：这4 次SEP 事件发生时平均太阳风速均在500 km·s–1左右，因此在文中尚未考虑太阳风速改变所造成的行星际磁力线的螺旋程度的改变，即认为这4 次事件中的最佳磁力线保持一致；强度峰值和峰值上升沿与SEP 事件的发生位置及太阳风速之间没有明显的相关性，表明发生当次SEP 事件时所处的空间环境对于事件的特征影响尤为重要。不过，对于处在日冕横向分布东西效应之外的SEP 事件，若要被地球卫星观测到必然要经过更长时间的太阳日冕区横向传输过程。因此，表2中的两次发生在东经位置的SEP 事件与其他两次事件相比，对应了强度相对更高的太阳耀斑等级，甚至是与X4 级别的大耀斑相关联。

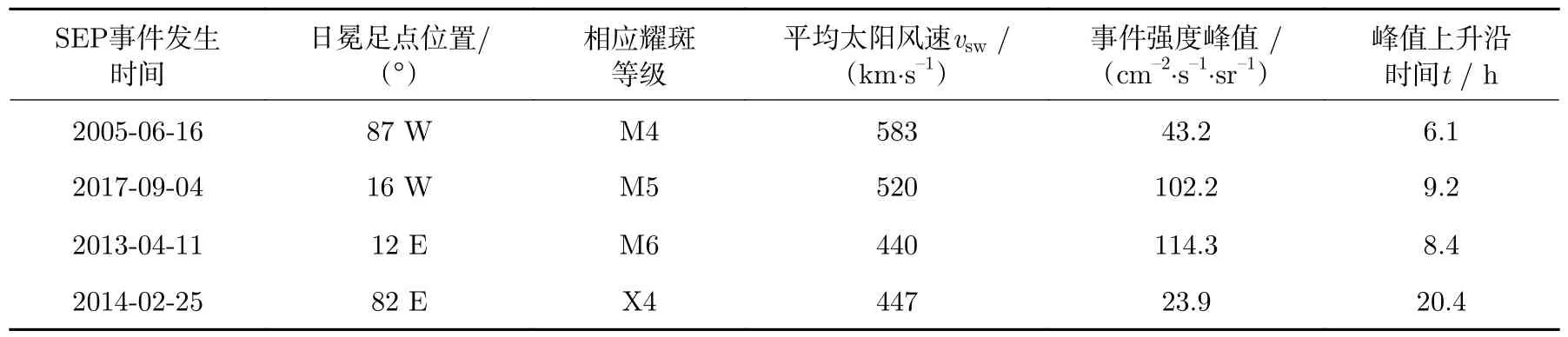
表2 四次不同日冕足点SEP 事件特征参数Table 2 Characteristic parameters of the four SEP events with different coronal-foot-point longitudes

3 结论与讨论

利用 NOAA 空间环境服务中心网站给出的SEP事件数据，统计了自1976－2017年期间记录到的217 次SEP 事件的日冕足点经度位置，并基于文献[19]给出的描述太阳高能粒子在行星际扩散的两相传输模型及其Green 函数解，对发生在不同日冕足点的四次SEP 事件进行了模拟研究，并针对模型中的多个传输参数开展了敏感性分析试验，主要结论如下。

（1）1976－2017年期间记录到的217 次SEP 事件的日冕足点经度位置主要集中在50°W 东西各50°附近，即0°W－100°W 之间，处在此范围内的SEP 事件共有143 次，占到事件总数的约65.9%，体现了SEP 事件日冕横向分布的东西效应。

（2）SEP 事件的日冕足点经度位置影响卫星探测到此次事件的时间和峰值，在相同条件下发生的SEP 事件越靠近最佳磁力线日冕足点，地球卫星越能及早探测到该事件，同时由于质子没有经过日冕区扩散消耗，探测到的SEP 事件峰值也越大。

（3）对于发生在非最佳磁力线日冕足点的SEP事件，太阳风速增大会造成质子更快地扩散至行星际空间，从而在一定程度上减少了经最佳磁力线传输至地球的数量，而当SEP 事件发生在最佳磁力线日冕足点时，太阳风速增大更加有利于该事件向地球扩散。

（4）日冕区扩散系数κ0与SEP 事件在日冕区的扩散过程相关，行星际径向扩散系数Kr的改变对于模拟结果的影响主要体现在峰值到达时间上，逃逸时间τe则是表征了粒子源的释放时间。

（5）SEP 两相传输模型能够较好地模拟发生在不同日冕足点的SEP 事件，不过对于处在日冕横向分布东西效应之外的SEP 事件，若要被地球卫星观测到必然会经过更长时间的太阳日冕区横向传输过程，因此往往也对应了更高强度的太阳耀斑等级。

本文的工作尚属初步探索，实际模拟的事例仅考虑了日冕足点的差异，需要探讨模型对于不同类型SEP 事件的适用性；模拟中选取了平均太阳风速为输入参数，有必要加入真实太阳风速以减少模拟误差；模拟针对的是黄道面内SEP 事件的扩散过程，没有考虑高能粒子在垂直黄道面的扩散过程。这些问题都有待在下一步的工作中深入研究，使之能够更加有效地用于SEP 空间天气预报。