考虑颗粒破碎的粗粒土一维压缩试验离散元模拟
吴远亮,徐宇冉,姬 静,石汉生
(1、广东省建筑设计研究院有限公司 广州 510010;2、上海交通大学土木系 上海 200240)
0 引言
粗粒土,常见的砂、砾等是土木工程界常用的建筑材料,被广泛地应用于土石坝、公路路基等建设工程中[1-3]。粗粒土很容易发生颗粒破碎现象,尤其是高应力状态下,颗粒破碎明显,引起粗粒土结构及级配发生变化,大大改变粗粒土如强度、压缩性等力学性质[4-6]。
很多学者对于颗粒破碎对压缩曲线的影响展开研究,开展了一系列室内压缩试验,取得了一些成果。马启锋等人[7]通过自行设计的高强加载压力室在三轴固液藕合试验机下对钙质砂进行侧限压缩试验,研究钙质砂高应力水平下的压缩和颗粒破碎特性,并用石英砂来进行对比研究。高应力下,钙质砂比石英砂压缩变形量大,钙质砂屈服应力在2 MPa 左右,远小于石英砂。NAKATA 等人[8]为了研究压缩线曲率和颗粒级配曲线的关系,对部分颗粒进行了染色处理并引入指标定量度量颗粒破碎程度。试验结果显示,良好级配分布的试样中,颗粒粒径越小,整体破碎的数量越多;颗粒粒径均一分布的试样中,颗粒粒径越大,越容易破碎。不过室内试验费时费力,试验过程中易出现不可控因素,且无法直观地观察到颗粒破碎过程。
近些年来,随着计算机技术的大力发展,采用离散单元法对于粗粒土一维压缩试验进行数值模拟成为主流。刘君等人[9]以双江口高土石坝为工程背景,利用二维颗粒流软件对堆石料在一定围压下的颗粒破碎情况进行模拟,结果与室内平面应变试验结果基本一致,说明用颗粒流方法进行数值模拟能够较好地再现堆石料的颗粒破碎特性。刘斯宏等人[10]使用DEM数值模拟计算了颗粒介质的双轴压缩试验,分析颗粒在等向压缩与剪切过程中颗粒细观结构的变化规律,推导出基于细观结构的颗粒介质屈服函数。数值模拟省时省力,可以再现颗粒压缩过程中的破碎规律,对于粗粒土压缩特性的探究具有重要意义。采用离散单元法模拟颗粒破碎有两种方法:①将基本小粒子进行捆绑,颗粒破碎意味着基本小粒子之间的粘结键断裂[11];②设定破碎准则,当颗粒受力超过设定的破碎强度后,删除原颗粒,用数个子代颗粒替代[12]。本文采用第二种方法,重点探究了粗粒土一维压缩试验中初始粒径尺寸、颗粒间摩擦系数、颗粒破碎情况、颗粒破碎准则对于压缩曲线中压缩特性的影响。
1 离散元试样制备
1.1 离散元试样制备及加载过程
首先,生成尺寸为60 mm×20 mm 的四面墙体,在墙体的内部空间内使用半径扩大法生成单一粒径大小为1 mm 的粗粒土颗粒,指定初始孔隙率为0.2,得到矩形试样。由于试样边界的转向部位颗粒很容易产生应力集中现象,且不同位置的颗粒间因重叠量的不同应力状态差异性很大,需要对该试样进行伺服处理,即通过不断调整水平和竖直方向的伺服速度,最大可能地释放颗粒间应变能,促使颗粒位置不断调整实现更均匀的孔隙率,直到调整所有边界的平均接触应力达到指定要求。得到初始试样如图1所示。

图1 一维压缩的数值模型及测量圆布置Fig.1 Numerical Model of One-dimensional Compression and Arrangement of Measurement Circle
对于考虑颗粒破碎的粗粒土一维压缩试验模拟,加载时,固定左右以及下侧这三面墙体,通过移动上侧墙体进行加载,模拟中加载模式采用力控制,每次给上侧墙体施加50 kPa 后,监测试样中颗粒的受力状态,破碎采用最大接触力原则,根据徐永福等人[13-14]推导出的单颗粒压缩破碎的尺寸效应:

式中:σf为颗粒破碎强度;σc为颗粒固有破碎强度,是材料固有性质,与粒径无关;D为单颗粒破碎的分维,在2~3 之间。当颗粒最大接触力大于由式⑴计算得到的单颗粒压缩破碎强度时,删除原颗粒,在原有位置等效替代为两个或数个同等大小的颗粒。为了保持质量守恒,二维情况下,对比原颗粒,新生成颗粒的总面积大小保持不变,但是这样会导致较大的颗粒重叠,所以需要一定的计算步数使颗粒间弹开,重新达到平衡状态后,再继续进行加载。
在加载的过程中,为了获取压缩过程中的loge~logσ曲线,需要记录上侧墙体的应力及应变,通过设置3个测量圆取平均值计算孔隙率,如图1所示。由于PFC-2D 是进行二维情况下的数值模拟,计算得到的孔隙率需要转化为实际的三维孔隙率,根据HOOMANS[15]提出的孔隙率转化计算式如下:
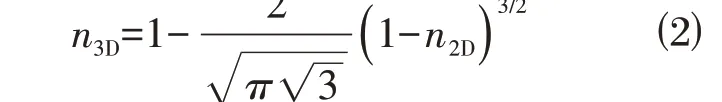
1.2 离散元本构模型及参数设置
颗粒间选取线性接触模型,接触力可分为线性和阻尼部分,如图2所示。线性部分即Fl提供线弹性、摩擦行为,阻尼部分即Fd提供黏性行为,均可分为法向和剪切方向,法向以下标n表示,剪切方向以下标s 表示。线性力通过恒定的法向和剪切刚度的线性弹簧产生,即kn及ks。线性弹簧不能维持张力,通过摩擦系数μ对剪切力施加库伦准则满足滑移条件。阻尼力由阻尼器产生,其黏度与法向和剪切临界阻尼比有关,即βn及βs。

图2 颗粒接触的本构模型Fig.2 Constitutive Model of Particle Contact
颗粒流模拟只能通过颗粒间的细观参数来反应材料的宏观参数,故细观参数的选择十分重要,参考相关文献及已有的数值模拟[16-17],最终确定模型模拟的参数如表1 所示。其中设置了材料的弹性模量E,可通过式⑷~式⑹计算出对应的法向刚度,再通过刚度比得到切向刚度。
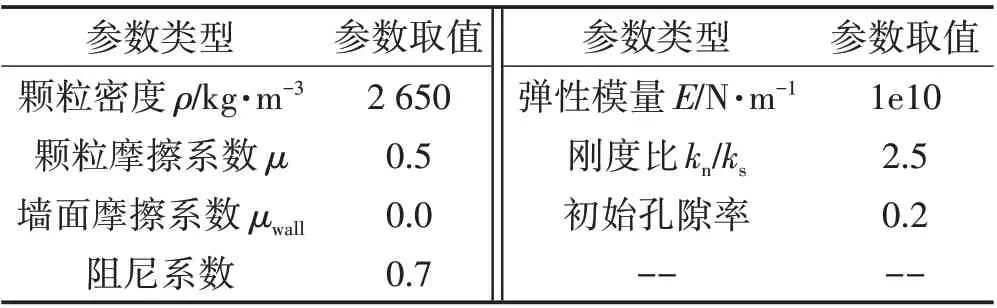
表1 一维压缩模型的参数取值Tab.1 Parameters of One-dimensional Compression Model

式中:r取两个颗粒间粒径较小颗粒的半径;L取两个颗粒半径之和。
2 模拟结果分析
2.1 压缩破碎过程
一维压缩过程中的颗粒大小及位移变化如图3所示,初始是单一粒径,为红色颗粒,当竖向应力达到10 MPa 时,颗粒已经发生了一部分的一级破碎,产生了黄色颗粒,基本未发生二级破碎;当竖向应力达到20 MPa 时,颗粒破碎十分明显,黄色颗粒进一步破碎为绿色颗粒,绿色颗粒进一步破碎,共产生了数代子颗粒,颗粒压缩明显,不过还有相当一部分大颗粒未达到破碎条件;当竖向应力达到30 MPa 时,可以看到不同粒径的颗粒较均匀分布在空间内,小颗粒环绕大颗粒形成了保护机制,试样十分密实,孔隙率很低。
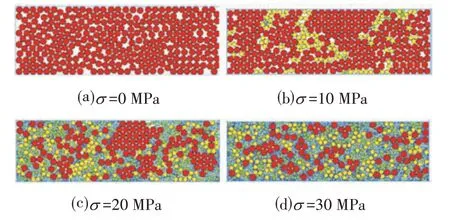
图3 一维压缩过程及颗粒粒径变化Fig.3 Change of Particle Size during One-dimensional Compression
2.2 压缩特性的影响因素
标准对照组的loge~logσ曲线如图4 所示,可将此压缩过程分成3个阶段。在点A至点B之间,颗粒主要在低应力下发生滑动旋转等颗粒排列,在点B至点C之间,颗粒受到高应力作用,发生大量颗粒破碎,破碎产生的小颗粒填补了大颗粒之间的孔隙,颗粒发生重排,产生更大压缩。将BC 这段线性关系的斜率定为压缩曲线的压缩系数λ;将曲率最大的点B定义为压缩曲线的屈服点,是两条渐近线的交点对应的曲线点,其对应的应力为屈服应力σy。在点C至点D之间,破碎产生的小颗粒保护大颗粒不再破碎,小颗粒由于自身强度较高也不会继续破碎,破碎不再是主要的变形机制,曲率趋于平缓。这与RUSSELL[18]的发现一致。

图4 标准对照组log e-log σ 曲线Fig.4 log e-log σ Curve of Standard Group
一维压缩过程中,为了探究初始粒径尺寸、粒间摩擦系数、颗粒破碎情况以及颗粒破碎准则对于试样压缩特性的影响,设置模拟对照组如表2 所示。其中颗粒破碎情况分为两颗粒、三颗粒、四颗粒破碎,如图5所示。删除原颗粒后在原位置将按照图5 生成次级颗粒,再经过一定计算步数使颗粒间弹开。颗粒破碎准则中对于标准组式⑴中的分维D取为2.5,对照组中D分别取为2.7、2.6、2.4及2.3。

图5 颗粒破碎情况Fig.5 Three Ways of Particle Crushing

表2 一维压缩模型对照组试验方案Tab.2 Control Group Setting of One-dimensional Compression Model
对于一维压缩试验数值模拟获取的loge~logσ曲线,有两个重要的参数用来描述压缩曲线的压缩特性,分别是屈服应力σy以及压缩系数λ,上文中已提到两个参数的获取方法。以初始粒径1 mm、粒间摩擦系数为0.5作为基本对照组,得到初始粒径、粒间摩擦系数、破碎情况以及破碎准则的影响如图6所示。
由图6⒜可以清楚地看到,随着颗粒初始粒径的增大,压缩曲线的斜率明显增大,即压缩系数增大,而屈服应力明显减小。已有的研究表明,曲线屈服意味着颗粒开始破碎,由于颗粒强度存在尺寸效应,颗粒初始粒径越大,对应的破碎强度越低,颗粒率先破碎,故粒径大的试样屈服应力较低。而初始粒径较大的试样破碎更明显,产生的子代颗粒更易填补到大颗粒之间的孔隙,故压缩性更明显,压缩系数较高。由图6⒝可知,随着颗粒间摩擦系数的增大,压缩系数也有明显增加,而屈服应力略有减小。当颗粒间摩擦系数较大时,可以将颗粒想象成表面凹凸不平的颗粒,对于这种颗粒,颗粒易于破碎,压缩曲线屈服应力较低,而压缩系数较大。而当颗粒间摩擦系数较小时,可以将颗粒想象为表面光滑的颗粒,对于这种颗粒,相同应力状态下较难破碎,屈服应力较大,而压缩系数较小。如图6⒞所示,颗粒破碎情况对于压缩曲线的压缩特性基本上没有影响,3 种不同破碎情况对应的loge~logσ曲线基本是重合的。如图6⒟所示,随着颗粒破碎准则中分维D的增加,压缩系数随之增大而屈服应力略有减小,屈服应力变化并不明显。虽然选取了5种不同的破碎准则,但是其对应的初始粒径即0.001 m粒径的破碎强度是一样的,设为40 MPa,故颗粒破碎开始时的应力相近,屈服应力变化不明显。但是分维D越大,次级颗粒强度越小,虽然初始粒径的强度一样,但次级颗粒破碎强度小的更易破碎,更易产生子代颗粒,破碎明显而压缩系数较大。
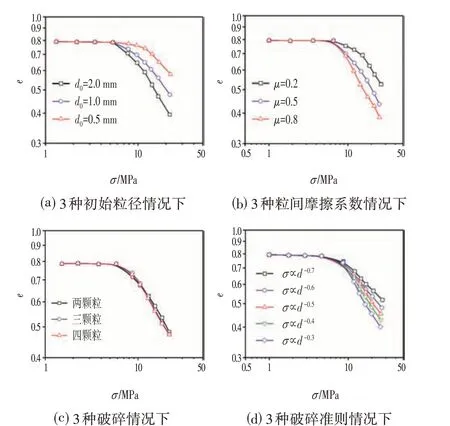
图6 log e-log σ 曲线Fig.6 log e-log σ Curves
综上,可以看出对于压缩曲线压缩特性影响最大的因素应为颗粒的初始粒径大小;其次为粒间摩擦系数,颗粒破碎准则对于压缩系数有较大影响而对屈服应力影响较小;而颗粒破碎情况对于压缩特性则基本没有影响。
3 结论
本文采用离散元软件PFC-2D对粗粒土一维压缩试验进行数值模拟,压缩过程中考虑颗粒破碎,得到了颗粒破碎情况和破碎规律。通过设置对照组,分别探究了初始粒径大小、颗粒间摩擦系数、颗粒破碎情况及颗粒破碎准则对于压缩曲线中压缩特性的影响,主要得到以下结论:
⑴一维压缩过程中,会产生明显的颗粒破碎现象,生成数代子颗粒,最终形成小颗粒保护大颗粒的相对稳定的状态。
⑵一维压缩过程中,颗粒首先在低应力下发生滑动旋转等颗粒排列。屈服点后,颗粒受到高应力作用,发生大量颗粒破碎,破碎产生的小颗粒填补了大颗粒之间的孔隙,产生更大压缩。而后颗粒不再破碎,曲线趋于平缓。
⑶随着初始粒径的增大,压缩系数增大,而屈服应力明显减小;随着颗粒间摩擦系数的增大,压缩系数增大,屈服应力减小;颗粒破碎情况对压缩曲线特性基本无影响;随着破碎准则中分维D的增大,压缩系数增大,屈服应力略有减小。
⑷初始粒径大小是影响压缩特性的主要因素,其次是颗粒间摩擦系数,破碎准则中的分维D主要影响压缩系数。

