非对称成本环境下两阶段随机成本共识模型的研究

□李焕欢 纪 颖 屈绍建

[1. 上海理工大学 上海 200093；2. 上海大学 上海 2004444；3. 南京信息工程大学 南京210044]

引言

群体决策是指群体成员就某一亟待解决的问题同时参与决策分析，并且每个成员都要充分发挥自己的智慧，发表不同的意见，最终共同找出解决问题的策略和途径[1～2]。为了就某个问题上达成一致意见，群体成员需要多次协商、讨论并且修改他们的初始意见和偏好，最终达成共识[3]。因此，群体决策往往优于个体决策，因为它是综合考虑所有参与决策专家的观点。通常情况下，共识达成过程的正常进行需要一个协调者，他将参与整个决策环节并且在整个过程中起到监督和引导的作用，最终推动群体意见向预期的共识意见发展。

为了促进共识的达成，群体决策中的协调者需要为决策者提供一定的补偿，只有这样决策者才会有意愿去改变自己的初始观点。在这个过程中，一方面主持人希望以最小的代价来促成共识，而另一方面专家则希望通过修改意见获得最大的补偿。基于协调者的角度，Ben Arieh等首先提出了最小成本共识模型，该模型由一个线性函数表示[4]。进一步地，由于不能保证所有决策者都会接受共识意见，基于这个思想，Ben Arieh等提出了达成共识的最大专家数的数学模型[5]。此外，一些学者指出共识达成过程中关于调整偏差的研究也是极其重要的。基于此，Dong等率先提出了最小调整共识模型，它可以尽可能多地保留决策者的初始意见[6]。Zhang等也对带有聚合算子的新的共识模型展开了研究[7]。近期，Zhang等针对共识达成过程中的最小调整或最小成本的反馈机制进行了综述，并在此基础上扩展了一些尚未解决的问题[8]。此外，决策问题中所涉及的共识成本机制也引起了越来越多学者的关注[9～10]。通常情况下，专家在修改初始意见时，有两个可以调整的方向，即向上调整意见和向下调整意见。基于这种思想，Cheng等提出了非对称调整成本背景下的最小成本共识的建模，该模型将共识成本分为向上或向下的调整方向[11]。这种建模方法是基于单位向上/向下调整成本、初始意见、妥协限度、免费调整阈值是确定值的情况，因而，是一种在确定决策环境下的建模形式。事实上，受专家的知识储备、历史信息和决策能力、信任程度[12]以及决策环境的影响，将会导致整个决策过程充斥着不确定性。但是，针对在不确定环境下关于非对称成本的最小成本共识模型的研究还比较缺乏，这使得这一研究方向有广阔的研究前景[12～14]。

本文研究了在非对称成本背景下，考虑到初始意见、单位调整成本、妥协限度和无成本调整阈值存在的多种情景，搭建三类两阶段随机成本共识模型，所提出的建模方法旨在不确定环境下进行调整意见来达成共识。在群体决策领域中，以往处理不确定性的理论方法有区间分析法[15～16]、模糊集[17～19]、概率论[20～21]、不确定性理论[22～23]、鲁棒优化法[24～25]等。虽然上述研究为决策者在不确定环境下进行决策提供合理性建议，但却忽略决策环境中可能出现的多种情景。事实上，在一些较为复杂的群体决策问题中，许多决策并不是同时进行的，而是按照时间顺序依次进行的。通常，决策可以被分为“此时此刻”决策和“观望”决策，其中“此时此刻”决策是在不确定性因素实现之前所做出的决策，也被称为第一阶段决策；“观望”决策是在不确定性实现后进行的决策，也被称为第二阶段决策。这种分阶段进行决策的思想被称为两阶段随机规划[26～27]，它作为一种处理不确定信息的有效理论，在金融经济[28～29]、供应链管理[30～31]等实际领域有着广泛的应用。随着在决策领域研究的不断深入，研究在不确定环境下共识的达成显得尤为重要。本文在非对称成本的前提下，考虑多个参数存在不确定的情况，提出了两阶段随机成本共识模型。特别地，在所构建的模型中，“此时此刻”决定是协调者综合各种因素给出的预期共识，而“观望”决策则是针对各种情景如何对意见进行具体修改。

本论文的主要贡献和创新性如下：（1）提出三种不同类型的基于非对称成本的两阶段随机成本共识的模型，考虑调整过程中由方向性所导致的总成本的差异，以及单位成本和个人初始意见不确定性。（2）考虑到两阶段随机成本共识模型处理的棘手程度，采用L形算法对其进行求解。通过将其与CPLEX求解器的结果比较，验证该算法的精准性与有效性。（3）将构建的两阶段随机成本共识模型应用于“退耕还林”政策，案例研究表明我们的研究可以帮助决策者更好地进行决策。（4）将构建的模型与确定环境下的共识模型进行对比，发现我们的模型具有更强的稳健性。

一、问题描述

群体决策问题是人们日常生活中极为普遍的活动，其中参与决策的所有专家的集合被记为E={e1,e2,···,en}，他们所提供的初始意见的集合被记为O={o1,o2,···,on}。由于决策者在进行决策过程中并不会只给出一种意见，更多的则是针对多种不同情景相应地给出不同的意见。本文假设专家的初始意见存在多种情景，用oi(ω)来表示，其中 ω 表示的是某一种情景。

由于决策者对问题认识的深度和广度以及利益的出发点不同，导致不同专家对于同一问题的决策可能不一致。为了能在规定的时间内达成有效的一致意见，协调者往往需要为决策者提供一定的补偿，以此来激励他们尽快完成意见的修改。需要修改意见的决策者的初始观点可能大于或小于共识意见，由此存在两个相反的调整方向。根据调整方向的不同，单位调整成本也是存在差异的，本文用来表示单位向上和向下调整成本。此外，用表示在某种情景 ω下在向上/向下方向上的单位成本。根据文献[32]中随机单位成本的确定方法，令为单位调整成本的集合，其中都是由随机生成，µc和 σc分别代表单位调整成本的期望值和方差。在这里，我们假设 µc为第一种情景的单位成本的取值，σc的取值为0.2，令共识意见为o′，协调者所要支付的总成本为 Φ。

在实际决策中，决策者不可能无限制地修改初始意见，他们只允许在一定范围内修改意见，换句话说，他们修改的行为是带有妥协限度的。此外，还存在一种情况，那就是决策者为了尽快地促进共识，允许在一定接受范围内修改意见是免费的，即无需协调者支付补偿。因此，本文在非对称调整成本的背景下，就三种不同的决策行为在不确定环境下进行建模。本文的主要目的是基于多种情景的决策环境，研究非对称成本下两阶段随机最小成本共识模型，以求得规定约束下的总成本。

二、两阶段随机最小成本共识模型

三、带有妥协限度的两阶段随机最小成本共识模型

四、带有无成本阈值的两阶段随机最小成本共识模型

五、L形算法

六、应用

针对现实世界中存在的不确定性决策问题，本文提出了两阶段随机成本共识模型，此外，将所提出的三种模型用来分析“退耕还林”政策。结果表明，所提出的两阶段随机成本共识模型具有较好的实用性。本文的数值实验均在笔记本电脑（Intel i5 CPU, 8GB RAM）上进行的。为了进一步验证算法的准确性，将本文提出的算法与CPLEX进行比较，发现两种方法可以得到相同的实验结果。然而，就计算时间而言，L形算法比CPLEX耗费时间更短。这恰恰说明了L形算法的有效性和准确性。

水土流失、荒漠化、生物多样性减少等一系列生态问题的出现，对生态安全构成了严重威胁[33]。如今，国家越来越重视自然环境保护，1999年，国家正式拉开了“退耕还林”政策的序幕。这一政策的提出促进了农田生态系统和森林草原生态系统的面积转化[34]。该项目可以提高植被覆盖率，加强农业用地的保护，特别是土壤和退化土地的恢复。“退耕还林”政策主要是依靠国家政策性补贴和巨大的经济投入，根据耕地面积，将耕地补偿的配额由政府分配给各省，各省分配给其地（市）、乡（区）、村（街道），由此向停止耕种的农民提供耕地补贴来回收土地。

然而，并不是所有参与的农民都同意补偿政策，如果存在分歧，则需要通过协商来解决。在进行协商的过程中，这些农民会参照其他地区的补贴政策，提出他们预期每亩地的补贴。为了使他们期望的补贴达成一致，协调者需要提供补偿来劝说他们修改初始补贴。在这个背景下，预期补贴和单位调整补偿具有不确定性。如果将地方政府和农户代表分别看作协调者和决策者，那么这个问题可以被看作是一个群体决策问题，并且可以用所提出的两阶段随机成本共识模型来解决。

本文的相关数据是参考文献[20]。假设有4个农户代表 {e1,e2,e3,e4}与政府代表人员共同参与到就“退耕还林”政策相关的土地补贴协商过程，用来描述不确定性的相关参数被模拟为三种情景。假设农户代表的意见在三种情景下取值的集合分别为o1(ω)={17,18.5,20}，o2(ω)={16,18,21}，o3(ω)={22,23,24},o4(ω)={18,20.5,23}（1 000元/亩）。我们假设在第一种情景下4位农户代表单位向上调整成本取值的集合分别为（1 000元），单位向下调整成本分别为（1 000元），另外两种情景的方向性单位成本的取值均由正态分布生成。此外，假设三种情景所占概率分别为p={0.2,0.4,0.4}。因此，将此问题应用到模型(1)，求解得到最优解和最优值为o′=23，Φ =3.16。

进一步地，在上述问题基础上，假设每位农户代表妥协限度被描述为不确定的，其取值分别为ε(ω)={{2,3,3,2},{3,4,4,3},{4,5,5,4}}(1 000元/亩)，将其应用到模型(2)。经过计算，得到最优解o′=19和最优值Φ =7.48。此外，假设每位农户代表的无成本调整的阈值是不确定的，其三种情景下的取值分别为θ(ω)={{3,2,1,2},{2,2,2,1},{3,4,2,1}}(1 000元/亩)，应用模型(3)来求解，计算得到o′=22和Φ =0.74。

为了验证算法的准确性，使用CPLEX求解器进一步计算，数值实验结果如表1所示。通过对比，可以发现两种方法求解得到的最优解和最优值均相同，但L形算法的求解时间更短。在表1中，通过比较三种两阶段随机成本共识模型的总成本，可以发现模型(2)的总成本最大，而模型(3)的总成本最小。出现这种现象的原因是模型(2)的专家的妥协是有一定限度的，相对而言对初始意见的坚持程度更高，只允许一定范围内修改意见，这将会导致需要更多费用来协调。相反，模型(3)允许每位专家都有免费的调整阈值，在阈值内调整是不需要提供补偿的，这使得总共识成本更低。总而言之，在非对称成本背景下，专家的容忍度和无成本调整阈值对在不确定环境下达成共识的补偿成本有重要影响。

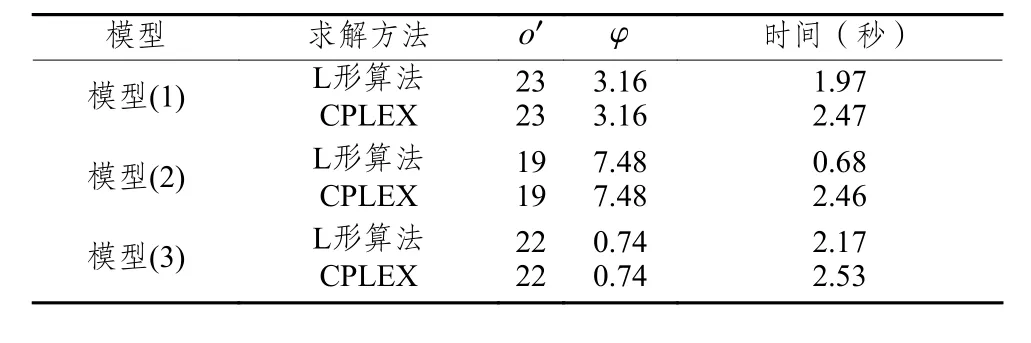
表1 模型求解方法的比较结果

七、对比分析和灵敏度分析

（一）对比分析

考虑单位调整成本是非对称的前提下，将最小成本共识模型[11]（MCCM-DC、 ε-MCCM-DC、TBMCCM-DC）与所提出的两阶段随机成本共识模型（模型(1)、模型(2)、模型(3)）进行对比分析。为了更好地进行模型间的比较，所提出模型的其中一种情景与文献[11]中的参数设置为相同的取值。观察表2的实验结果，可以发现，在考虑三种不同情景时，两阶段随机成本共识模型的总成本可能低于或高于最小成本共识模型的总成本，这与多种情景的具体取值有关。结果存在差异的原因在于最小成本共识模型只考虑单一情景，而两阶段随机成本共识模型综合考虑多个参数的多种情景，使得模型更加复杂，更加适用于实际的决策环境。

表2 不同成本共识模型的对比结果

（二）灵敏度分析

接下来，我们分别对三种类型的两阶段随机成本共识模型针对向上和向下单位调整成本进行灵敏度分析，观察其对总共识成本的影响，其中所用到的数据均来自于参考文献[20]。这里我们将灵敏度分析分为两部分，包括局部灵敏度分析和全局灵敏度分析，其中局部灵敏度分析只允许单个专家的测试参数（向上、向下调整成本）发生变化，其他参数保持不变；而全局灵敏度分析则是针对所有专家的测试参数（向上、向下调整成本）同时进行相同的变化。

1. 向下单位调整成本的灵敏度分析

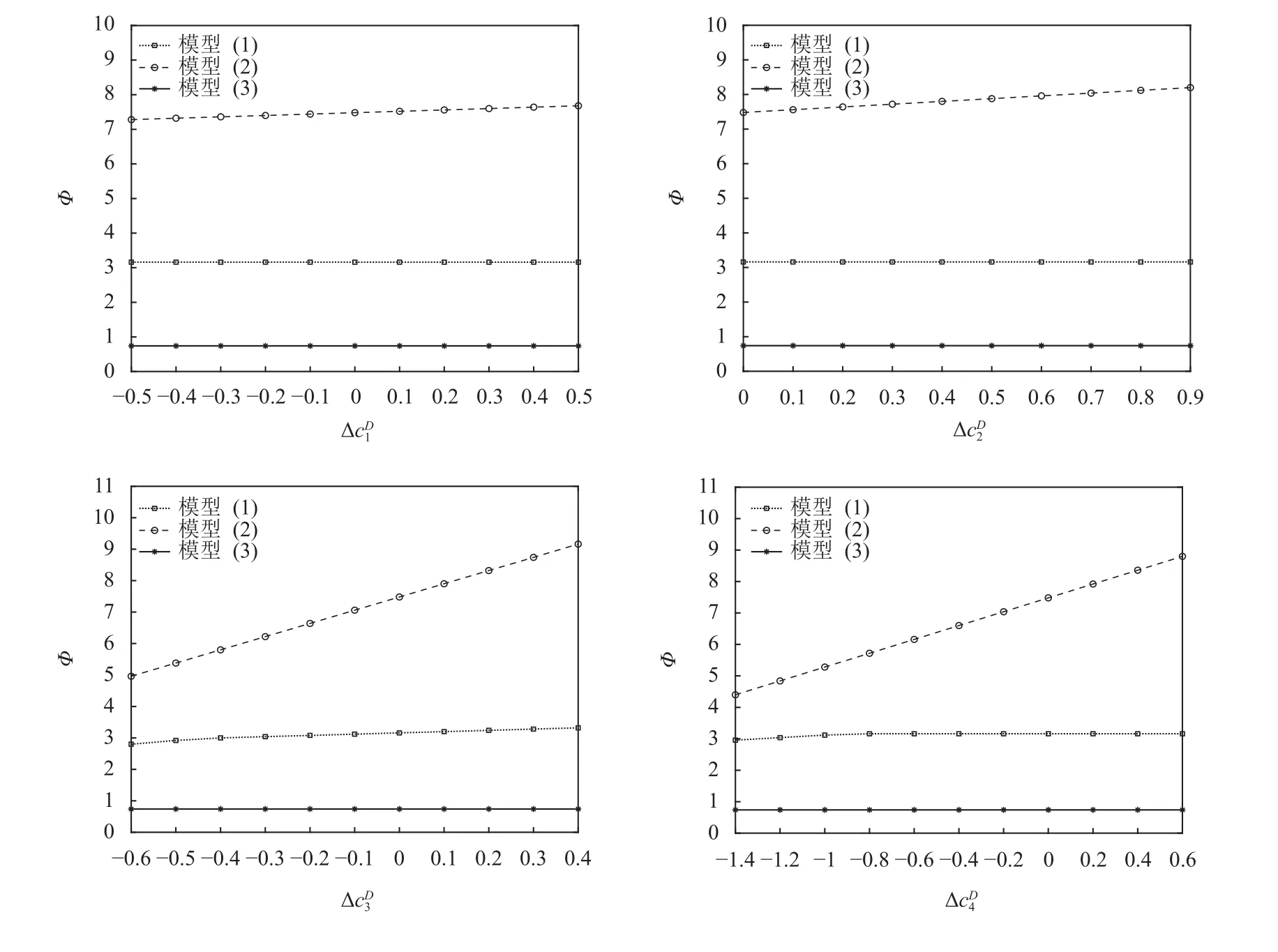
图1 局部调整成本对总共识成本的影响

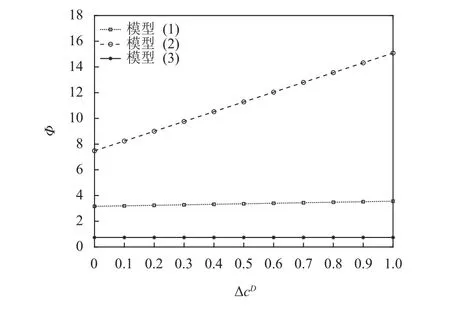
图2 全局向下调整成本对总共识成本的影响

2. 向上单位调整成本的灵敏度分析

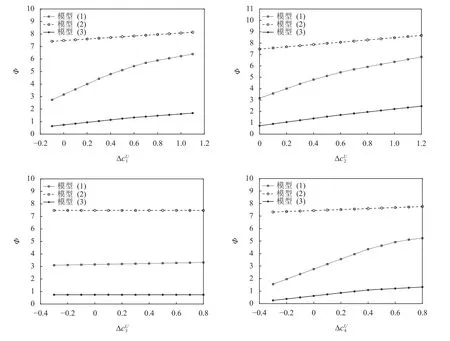
图3 局部向上调整成本对总共识成本的影响

另一方面，关于全局灵敏度分析方面，观察ΔcU对总共识成本的影响，变化趋势如图4所示。当所有专家就向上方向的单位成本同时增大时，总体上成本也会朝着增大的方向移动，换句话说，两者呈现正相关性。这说明在一定变化范围内，对于所给定的数值案例来说，如果所有的同时发生变化，两阶段随机成本模型对单位向上成本是敏感的。

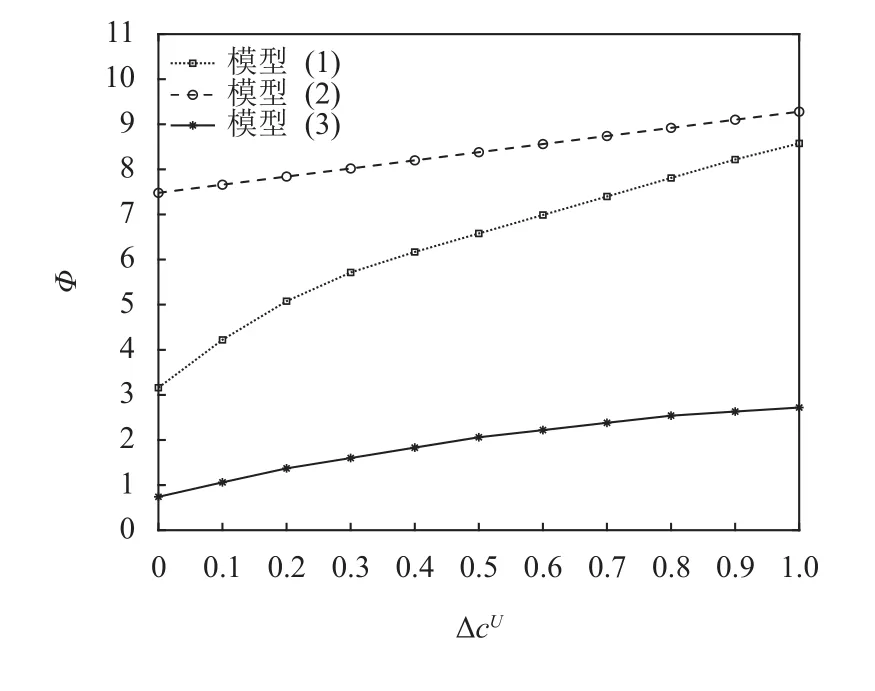
图4 全局向上调整成本对总共识成本的影响

八、结论与展望

本文研究了在不确定决策环境背景下，提出了三类非对称成本环境下两阶段随机成本共识模型，即两阶段随机最小成本共识模型、带有妥协限度的两阶段随机最小成本共识模型、带有无成本阈值的两阶段随机最小成本共识模型。

与以往的研究相比，本文具有以下优点。首先，所提出模型的显著特点是根据决策时间将决策过程分为两个阶段进行，其中第一阶段的决策为预期的共识，第二阶段的决策为根据预期共识对初始意见进行调整。此外，与以往共识模型的处理方式不同，本文针对性地给出L形算法来求解所提出成本共识模型。最后，将模型与“退耕还林”政策中关于土地补偿的案例相结合，通过数值结果、对比分析以及灵敏度分析对模型进行验证。

基于目前的研究，指出几个未来的研究方向：（1）面对不确定的决策环境，决策者出于保守起见往往会考虑最差的情形，当前应对最差情况有两种处理方式：一种是采用风险函数的手段，将风险降到最小；另一种是采用鲁棒优化的数学手段进行解决。因此，研究两阶段随机成本共识优化问题的最差情况是一个颇有前景的研究方向。（2）本文是基于小规模的群决策问题展开研究的，但是，在实际的决策过程中，决策者面临的决策问题往往呈现大规模的趋势。因此，研究在不确定决策环境下基于大规模群体的共识优化模型显得尤为重要。（3）语言偏好关系是处理主观判断的有效方法，决策者可以通过语言变量表达自己的意见[35]。近年来，基于语言偏好关系的共识建模作为处理共识建立的重要方法得到了广泛应用。因此，接下来的工作可以将本文所提出的建模思想与偏好关系相结合。