轴向拉伸下非粘结柔性管抗拉铠装层力学响应*
汤历平 姚 红 罗 衡 宋柯楠 石咏衡
(1.西南石油大学机电工程学院 2.中海油安全技术服务有限公司 3.国家石油天然气管网集团有限公司油气调控中心)
0 引言
油气勘探开发从陆地转向海洋是当前的大趋势,恶劣的海洋环境给油气资源运输管道的研究与设计带来了诸多挑战[1]。海洋非粘结柔性管相比传统的钢管具有更好的柔韧性、适用性和可回收性,成为“海洋石油生命线”,承担着水上浮式生产系统和水下生产系统间的重要运输任务[2]。
海洋非粘结柔性管结构复杂,各层功能不同且相对独立,复杂的结构以及各层结构可能出现不同种类的损伤和失效也使得对柔性管的研究变得更加困难[3]。即便如此,国内外学者在此领域仍做了大量的研究工作,主要的研究方法是解析法和有限元法。在假设无摩擦的条件下,S.SAEVIK 和N.H.OSTERGAARD 等[4-5]基于弯曲梁平衡系统,推导出一系列高阶微分方程来表示柔性管的本构关系和平衡条件,预测了柔性管在载荷下的不稳定性,但是该假设使结果有一定的局限性。S.SAEVIK[6]提出基于轴对称效应的应力预测模型来表示柔性管抗拉铠装层弯曲应力状态,并用相应的试验验证了该公式在动态应力和疲劳方面的性能,结果表明预测模型精度因子较高。M.A.VAZ等[7]借助有限元方法建立柔性管完整模型来预测管道的几种不同的失效模式。A.EBRAHIMI 等[8]通过建立连续介质有限元模型,研究了轴对称加载条件下非粘结柔性管的机械响应。相对于完整模型计算时间长且不易收敛的特点,DE J.M.R.SOUSA等[9-10]利用壳理论刚度等效的原理,将复杂的螺旋键结构等效为各向异性壳,但假设不存在各层自身结构之间的摩擦和其他相互作用,并且该模型也不能用于单独研究某一特定层的力学响应特性。E.R.MALTA 等[11]则将柔性管骨架层和抗压层等主要抵抗径向载荷的层简化为解析刚体,研究了抗拉铠装层在轴向压缩载荷下的力学性能,但这种方式可能导致模型计算结果偏小。考虑到层间影响,ZHANG H.C.等[12]通过罚函数法和拉格朗日乘数法将相邻层间的几何关系引入到模型中。周阳等[13]利用ABAQUS 软件分析了在层与层之间的摩擦接触因素下非金属非粘结软管拉伸状态下的力学性能。
笔者在总结各类研究方法的优劣之后,进一步对柔性管的拉伸响应进行研究。区别于传统的简化建模方式,本文采用有限元法建立了对研究拉伸载荷响应更为合理的等效模型,并通过试验数据对模型进行了验证;在此基础上,结合实际工况与柔性管的结构特性,对比分析了抗拉铠装层出现损伤之后对拉伸载荷的响应,并求得了在包括外压和扭矩在内的不同外载荷下柔性管的拉伸刚度,得到了组合载荷对柔性管拉伸刚度的不同影响规律。
1 非粘结柔性管结构
典型的非粘结柔性管结构如图1 所示,由金属层和聚合物层构成。其中,金属层包括骨架层、抗压铠装层和抗拉铠装层,为主要受力结构层;聚合物层包括内压密封层、抗磨层和外护套层。

图1 典型的非粘结柔性管结构Fig.1 Structure of a typical unbonded flexible pipe
骨架层形成自锁结构,主要用于抵抗外压,防止外压导致的非粘结柔性管压溃失效;内压密封层用于输送油气,且由于位于骨架层和抗压铠装层之间,可防止骨架层和抗压铠装层发生摩擦;抗压铠装层主要抵抗内压载荷,同时也抵抗部分外部静水压力,其截面形式主要有Z 形、C 形和T 形;抗磨层位于金属层之间,用于减少金属层之间的接触和摩擦,不承受抵抗载荷的作用;抗拉铠装层主要承受轴向力和扭转,为管道提供一定的拉伸刚度,由矩形截面钢带螺旋缠绕而成,一般为偶数层且铺设角度相反;外护套层主要用于隔离海水,防止海水进入管道腐蚀金属层。
2 有限元法建模
2.1 数值简化模型
由海洋柔性管的组成可知,骨架层、抗压铠装层和抗拉铠装层这一类螺旋缠绕结构是管道的主要构成形式。该结构涉及到的自由度众多,网格划分过于复杂,因此建立一个完整的三维柔性管模型是一项极其繁重的任务。根据文献[14-15] 对壳体理论的研究,将柔性管骨架层和抗压铠装层进行简化,则螺旋结构等效示意图如图2 所示。
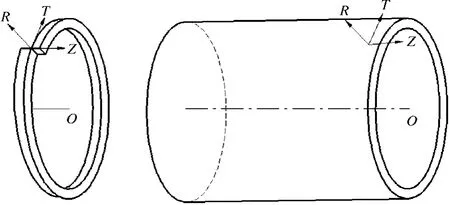
图2 螺旋结构等效示意图Fig.2 Equivalent schematic diagram of helical structure
根据壳体理论得出各向异性壳的轴向拉伸刚度(EA)S、弯曲刚度(EI)S和扭转刚度(GJ)S,分别表示为:
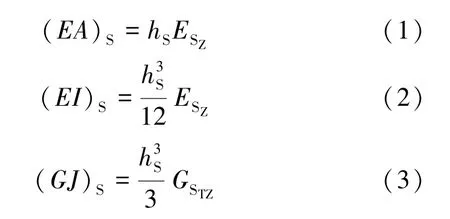
式中:hS为壳单元的等效厚度,ES为壳的等效物理参数,GSTZ为壳的等效几何参数。
螺旋键的拉伸刚度(EA)t、抗弯刚度(EI)t和扭转刚度(GJ)t分别表示为:

式中:E、G分别为各向异性壳和螺旋键的弹性模量和剪切模量,I、J分别为各向异性壳和螺旋键的惯性矩和极惯性矩,Ieq、Jeq分别为各向异性壳和螺旋键的等效惯性矩和等效极惯性矩,A、Lp和n分别为螺旋键的截面面积、螺距和键的数目。
当各向异性壳与螺旋键的拉伸刚度、弯曲刚度和扭转刚度分别相等时,能够得出各向异性壳的等效厚度、等效物理和等效几何参数,具体表达式为:
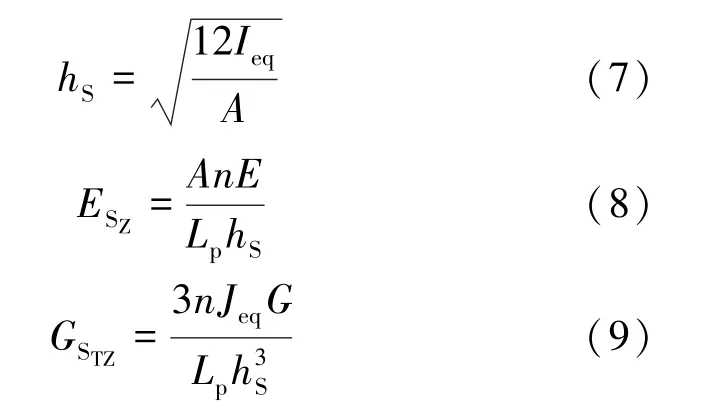
2.2 有限元模型
使用有限元软件建立了ø63.5 mm 非粘结海洋柔性管的三维数值模型,模型的几何尺寸数据来自文献[16]国际船舶和海洋结构委员会试验用的标准柔性管,其中骨架层弹性模量为1.90×105MPa,泊松比为0.30,螺旋角度为-87.5° (顺时针旋转方向),截面尺寸为28.0 mm×0.7 mm;内压密封层弹性模量为2.84×102MPa,泊松比为0.29;抗压铠装层弹性模量为2.07×105MPa,泊松比为0.30,螺旋角度为-85.5° (顺时针旋转方向),截面尺寸为9.25 mm×6.20 mm;抗磨层弹性模量为3.01×102MPa,泊松比为0.29,截面尺寸为30.0 mm×1.5 mm;抗拉铠装层弹性模量为2.07×105MPa,泊松比为0.30,内部抗拉铠装层螺旋角度为-35.0° (顺时针旋转方向),外部抗拉铠装层螺旋角度为35.0° (逆时针旋转方向),截面尺寸为6 mm×3 mm;外护套层弹性模量为4.50×102MPa,泊松比为0.29,螺旋角度为-84.0° (顺时针旋转方向),截面尺寸为75.00 mm×0.06 mm。
柔性管结构中,骨架层、抗压铠装层和抗拉铠装层都是螺旋结构,根据等效理论都可以等效为各向异性壳,但抗拉铠装层主要承受拉伸载荷,为了分析拉伸载荷下柔性管的响应,仅对其余两层进行等效建模。得到的有限元模型以及网格划分情况如图3 所示。

图3 有限元模型建立及网格划分结果Fig.3 Establishment and grid division results of the finite element model
为提高计算精度,网格采用实体单元中六面体八节点缩减积分单元(C3D8R),其中一条内抗拉铠装层的单元数为840,节点数为1 899;外抗拉铠装层的单元数为872,节点数为1 971。模型中存在较多的非线性接触,因此采用接触面之间的法向接触为“硬”接触,接触面切向接触定义恒定的库伦摩擦因数,在本模型中摩擦因数设置为0.1[17]。边界条件设置为一端固定,另一端设置耦合到参考点,根据工况进行加载。由于内压主要对抗压铠装层产生影响,而外压对抗拉铠装层影响较大,所以模型仅考虑外压作用而忽略内压的影响。
需要说明的是,为减少模型计算量并使模型更易收敛,选择准静态方法来分析模型。准静态方法是指人为地将静平衡问题转化为动平衡问题的一种加载方法。为评估这种方法的准确性,认为当系统的动能仅为内能的一小部分时,这种方法的结果可靠[18]。
3 结果与讨论
3.1 有限元模型的验证
为了评估海洋柔性管在承受载荷时它本身抵抗变形的能力,业界定义了柔性管等效的拉伸、压缩、扭转和弯曲刚度。当受到拉伸载荷F 时,柔性管的轴向伸长量为ε,则等效拉伸刚度K的表达式如下:

一般在模型验证时,除了对比载荷与伸长量曲线之间的非线性本构关系之外,还用等效拉伸刚度K的差值来证明模型的准确性。
文献[16] 的试验中,10 家研究机构都对标准的ø63.5 mm 海洋柔性管的拉伸刚度做了试验分析,将数值模型与试验所得的平均值做比较。试验中为体现严谨性,分类讨论了柔性管两端能自由旋转和不能自由旋转两种情况,结果表明这两种工况并不影响拉伸刚度。
柔性管拉伸载荷下整体应力分布云图如图4 所示。由图4 可以看出,应力主要分布在两层抗拉铠装层,这与柔性管的结构设计原理相符,同时也能表明简化模型的科学性。当柔性管两端自由旋转时,试验结果平均值与模型的对比如图5 所示。图5 显示试验平均值得到的拉伸刚度为128 MN,而有限元模型得到的拉伸刚度值为134 MN,仅有4.6%的误差值。图6 还展示了有限元模型的两端是否限制自由旋转的不同情况(工况A 为自由旋转,工况B 为不能自由旋转),结果得到了相似的拉伸刚度,这样的结论也与试验结果一致。在六面体单元的基础上,对上述模型增加网格数量,仿真结果表明网格数量对轴向拉伸刚度的影响可忽略不计。由此说明,模型可用于本文中对柔性管拉伸载荷的研究分析。

图4 柔性管拉伸载荷下整体应力分布云图Fig.4 Cloud chart of overall stress distribution of the flexible pipe under tensile load

图5 拉伸载荷下柔性管的轴向相对伸长量Fig.5 Relative axial elongation of the flexible pipe under tensile load

图6 两种工况下柔性管的轴向相对伸长量Fig.6 Relative axial elongation of the flexible pipe under two conditions
3.2 柔性管抗拉铠装层外层损伤对结果的影响
海洋柔性管在正常工况下除了承受管内介质的重力之外,还需要承受自身管体的重力,因此需抵抗较大的拉伸载荷[19]。本文的有限元仿真模型参考文献[16]中所用载荷,采用500 kN。柔性管结构中抗拉铠装层是为抵抗拉伸载荷而设计,因此抗拉铠装层的完整性对柔性管力学性能至关重要。抗拉铠装层一般是由偶数层方向相对的螺旋钢带缠绕而成,在柔性管的生命周期内,不论是制造、安装还是正常工作都有可能对抗拉铠装层产生损伤。为此,模拟了抗拉铠装层的损伤情况,研究了当抗拉铠装层外层的钢带损伤1 根和2 根情况下的响应,并进行对比分析。
图7 为抗拉铠装层钢带损伤模型以及有限元计算得到的局部应力分布云图。假设钢带存在划伤约1.5 mm 深的半圆形凹槽,可以发现柔性管出现比较明显的应力集中,损伤处是整个柔性管的最大应力点,这种应力集中会影响到柔性管的使用寿命,疲劳断裂一般会首先发生在应力集中处。

图7 抗拉铠装层钢带损伤模型以及计算结果应力分布云图Fig.7 Model of tensile steel tape armour with damage and cloud chart of calculated stress distribution
当外抗拉铠装层钢带损伤时,柔性管整体的轴向相对伸长量如图8 所示。由等效刚度的表达式可以求出柔性管外抗拉铠装层损伤1 根和2 根时的拉伸刚度分别为131 和130 MN,比无损伤时刚度仅降低了约2%,这表明损伤数目在1 根和2 根时对整体的拉伸刚度影响不大。进一步对每一根钢带的轴向应变量进行统计,结果如图9 所示。正常情况下有限元模型得到的结果显示:柔性管每根钢带呈均匀伸长,应变量相等;当出现损伤时,损伤的钢带显示了更大的应变量,应变相对于正常的钢带增大了约3%,且损伤钢带邻近的钢带应变量也相对增大,但从整体上看,损伤数量为1 根和2 根时最大轴向应变量相差并不明显。

图8 外层钢带损伤柔性管在拉伸载荷下整体的轴向相对伸长量Fig.8 Relative axial elongation of the flexible pipe with outer layer steel tape damage under tensile load
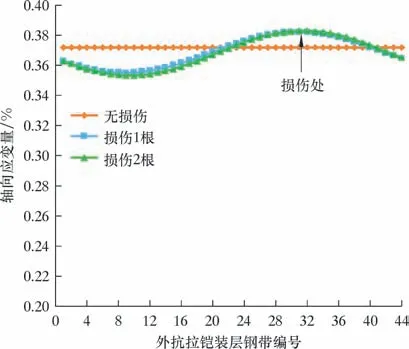
图9 抗拉铠装层外层钢带的轴向应变量Fig.9 Strain of the outer layer of tensile steel tape armour
3.3 柔性管抗拉铠装层内层损伤对结果的影响
抗拉铠装层的内层与外层有着相反的螺旋方向,因此再对内层进行相似的拉伸响应分析。当内抗拉铠装层损伤1 根和2 根时柔性管整体的轴向相对伸长量如图10 所示。内层损伤的影响结果显示与外层类似,当损伤数目较小时,柔性管整体刚度减小不明显,从数值计算结果来看仅有2%~3%的降低值。图11 为内抗拉铠装层40 根钢带在不同工况下的轴向应变量,结果显示损伤钢带后得到的应变量不相等,损伤一侧的钢带应变量普遍大于正常钢带一侧的应变量,并且同样发现损伤数目为1 根和2 根时,钢带轴向应变量的最大值相差也比较小。

图10 内层钢带损伤柔性管在拉伸载荷下整体的轴向相对伸长量Fig.10 Relative axial elongation of the flexible pipe with inner layer steel tape damage under tensile load

图11 抗拉铠装层内层钢带的轴向应变量Fig.11 Strain of the inner layer of tensile steel tape armour
综合上述两类损伤情况,柔性管内外抗拉铠装层损伤对拉伸刚度的影响如表1 所示。由表1 可知:抗拉铠装层内层和外层钢带损伤数目较小时,对柔性管的整体拉伸刚度都会有轻微的降低效果,但影响较小;当损伤数目为2 根时,柔性管的整体拉伸刚度减小量仅为3%。通过分析应力分布发现,两层钢带的损伤都会发生应力集中现象,从长远角度上讲,这对柔性管的使用寿命不利。
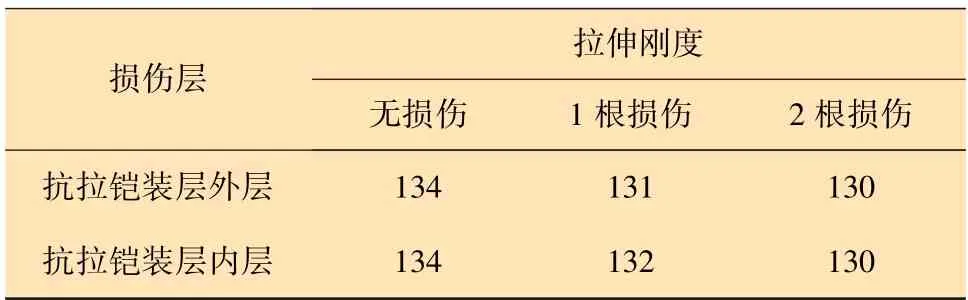
表1 柔性管内外抗拉铠装层损伤对拉伸刚度的影响 MNTable 1 Effect of the inner layer and outer layer steel tape damages of the tensile armour on the tensile stiffness of the flexible pipe MN
3.4 外界静水压力对柔性管响应的影响
深海作业中柔性管还受到巨大的静水压力的作用[20],分别讨论了当外界静水压为5 和10 MPa 时柔性管在拉伸载荷下的响应。不同外压下柔性管轴向相对伸长量对比如图12 所示。由图12 可以看出:外压的存在使拉伸刚度增大明显,经过数值计算结果也发现,当外压为5 MPa 时,柔性管的刚度增大了约40%;当外压为10 MPa 时,增强的效果在前者基础上变化不大。
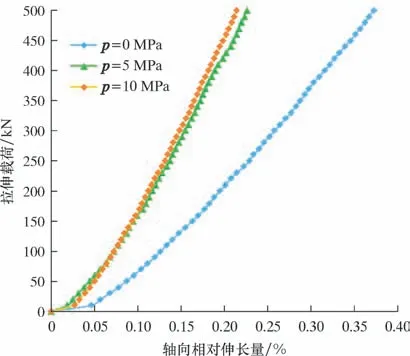
图12 不同外压下柔性管轴向相对伸长量Fig.12 Relative axial elongation of the flexible pipes under different external pressures
从柔性管的结构分析,柔性管各层相对独立,但是层与层之间乃至一层的每根钢带之间都存在间隙,拉伸载荷下各层间隙逐渐减小,并会出现相对滑移现象。当存在外载荷时,相当于给柔性管施加了一个夹紧力,夹紧力能够提前让层间的间隙减小,增大库伦摩擦,阻碍相对滑移发生,这样也就增大了柔性管的拉伸刚度。但外界静水压力不能超过极限,柔性管整体如果承受过大的夹紧力,会使内部骨架层或抗压铠装层压溃或塌陷[21],从而导致柔性管失效。
3.5 扭矩对柔性管响应的影响
海洋中流动的海流不仅会使柔性管发生涡激振动,还会对柔性管产生剪切和扭转作用[22-25]。为讨论扭矩对柔性管拉伸载荷响应的影响,根据实际工况分别对柔性管施加顺时针1 500 N·m 和逆时针4 000 N·m 的扭转载荷[16],结果如图13 所示。不同扭转载荷下拉伸刚度都会降低,顺时针扭转和逆时针扭转得到的结果是拉伸刚度减小量分别为7%和10%。造成这种结果的原因跟施加外载荷的原理正好相反,当螺旋结构受到方向相反的扭转载荷时,螺旋结构出现一种向外扩张的趋势,使各层间隙变大,柔性管在拉伸载荷下就更容易伸长。
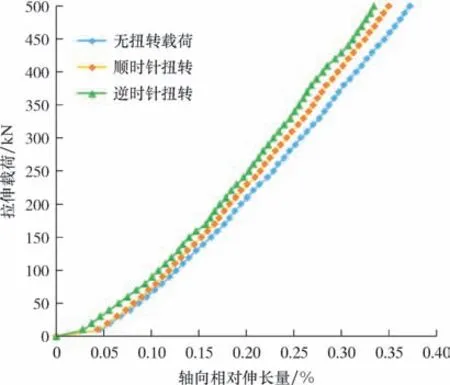
图13 扭转载荷下柔性管的轴向相对伸长量Fig.13 Comparison of relative axial elongation of the flexible pipe under torsional load
4 结论
根据各向异性壳与螺旋键刚度等效的原理,将柔性管骨架层和抗压铠装层等效为各向异性壳体,建立了计算效率更高的有限元简化模型。在标定模型之后,根据实际工况模拟了柔性管在拉伸载荷下的响应,求得了柔性管拉伸刚度。此外,考虑抗拉铠装层的损伤以及其他外界载荷对柔性管拉伸刚度的影响,分别对几种情况进行模拟讨论,得到以下结论:
(1) 通过刚度等效原理建立的有限元等效模型计算结果与试验平均值得到的拉伸刚度结果偏差较小,拉伸载荷和伸长量曲线也满足试验结果的非线性本构关系,柔性管两端能否自由旋转并不影响柔性管的拉伸刚度。
(2) 柔性管抗拉铠装层的损伤会产生明显的应力集中,此现象会加快柔性管的疲劳损伤甚至发生疲劳断裂,对柔性管整体的拉伸刚度影响较低,局部分析则发现损伤的钢带出现更大的应变量。横向对比表明抗拉铠装层的外层损伤与内层损伤对拉伸刚度的影响差别并不明显。
(3) 相对于其他外载荷,适当大小的静水压力会增强柔性管的拉伸刚度,但过大的静水压力会使柔性管骨架层压溃或塌陷,而扭矩则会相对降低柔性管的拉伸刚度。研究结果对柔性管的设计制造以及应用中预测柔性管的刚度变化起到参考作用。

