海绵城市绿色屋顶降雨径流模型构建及建议研究**
李鹏程,郝 放,赵建利
(1.河北水利电力学院沧州市遥感与智慧水利技术创新中心,河北 沧州 061001;2.中水北方勘测设计研究有限责任公司,天津 300222;3.河海大学水利水电学院,江苏 南京 210013;4.北京市水科学技术研究院,北京 100048)
城市水生态文明体系构建要求对水资源开展有效保护及合理利用,综合整治城市发展过程的水环境问题,是城市可持续发展的关键因素之一。海绵城市是通过构建低影响开发措施,包括绿色屋顶、植草沟、生物滞留池等,净化并截留降雨,对城市雨洪进行调控,对城市水生态文明体系构建具有积极促进作用。
对海绵城市低影响措施的研究主要通过理论分析、水文模型及实验分析进行,其中,水文模型是通过一定的数学物理模型及边界条件的设定,模拟降雨产流过程[1-5],将实际降雨过程概化处理,因此模型构建过程中参数的选取直接影响模型模拟的精度。本文通过建立绿色屋顶降雨产流模型,并设定初始条件和边界条件,进行模型率定及参数敏感性分析,以对提高模拟降雨产流精度。
1 模型构建及研究方法
1.1 降雨径流模型
运用HYDRUS-1D计算模拟绿色屋顶削减降雨径流过程,用它可以解算在不同边界条件制约下的数学模型,模型能够模拟溶质迁移以及多孔介质饱和-非饱和渗流区水、热过程,全面融入植物根系吸收、热运动、水分运动、溶质运移以及土壤持蓄作用[6-7],可不受限制地选择大气边界、渗水边界恒定水头、排水沟、通量边界、自由排水边界等,对构建的计算模型方程进行运算求解,并运用Crank-Nicholson有限差分法来进行时间离散计算,运用Galerkin有限元法进行空间离散,此模型可用于模拟水在土壤中的移动过程。
1.2 土壤水运动方程
土壤水运动方程:局部饱和的多孔刚性介质中的一维土壤水运动,若假设空气对水流过程影响不大且忽略热力梯度的影响,则可用Richard方程进行描述。

其中,h为压力水头[L],θ为体积含水率[L3L-3],t为时间[T],x为空间坐标[L],S为SinkTeam[L3L-3T-1],α为水流方向与竖直方向的夹角。非饱和水力传导度函数:

式中,KS为饱和水力传导度,Kr为相对水力传导度。
1.3 非饱和土壤水力特性
1.3.1 模型原理
非饱和土壤的水力特性,土壤含水量θ(h)与水力传导度K(h)与压力水头高度呈非线性关系。HYDRUS允许使用3种不同的水力特性模型[Brooks and Corey 1964;van Genuchtem 1980;Vogel and Cislerova 1988]。

本文模型采用van Genuchtem模型。
1.3.2 van Genuchtem模型
由统计上的气孔分布模型Mualem获得根据持水参数所获得的非饱和水力传导度函数:
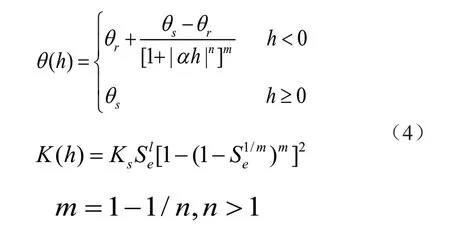
上述方程包括5个独立参数θr,θS,α,n,K;其中,水力传导度方程的气孔连接系数l对多种土壤估计得0.5。
以上这些参数,以现场取土在室内测得的数据及HYDRUS提供的基本土壤数据中的数值作为初始值,根据实际观测的土壤水分运动过程经过率定获得。
1.4 初始条件和边界条件
在模拟土壤水运动过程中需设定土壤剖面的初始条件,设定初始含水率值。含水率:θ(z,t)=θo(z),t=0。
在土壤剖面顶部(z=L)或底部(z=0)必须指定以下边界条件之一:

式中,h0[L]与q0[LT-1]为边界上压力水头与土壤水流的规定值。
HYDRUS-1D中又将上述边界条件进行了细化,其中,上边界条件包括定通量边界、土壤表层大气边界、定水头边界、土壤表层径流大气边界、变通量边界和变水头边界;下边界条件包括定通量边界、变通量边界、定水头边界、变水头边界、渗漏面边界、自由排水边界、水平排水边界条件和深层排水边界。本研究中模型采用自由排水边界和渗漏面边界。
2 模型率定及参数敏感性分析
分别选取不同绿色屋顶在不同降雨条件下所模拟得出的出流值与实测值进行对比,完成对模型的率定和验证。
检验率定和验证是否达到要求,通过以下3个统计量评定:1)均方误差RMSE;2)相关系数R2;3)平均相对误差MRE。

式中:N是观测值的个数,Oi表示第i个观测值,Pi表示第i个观测值的模拟值。
模型在模拟土壤水运动过程中的输入数据主要包括时间信息、几何信息、土壤水力特征参数、初始条件、边界条件以及土壤剖面信息等[8-9]。绿色屋顶的模拟时间依据试验的降雨和产流时间来确定[10-11];模拟的土壤层厚度为填料层厚度和种植层厚度之和,且不同的绿色屋顶有不同的厚度,分为10 cm和20 cm。输入各填料层对应的土壤水力特征参数;模拟的初始条件为初始时刻土壤剖面的含水率值;上边界条件均为土壤表层的大气边界条件,由于模拟时间较短(小于5 h),不考虑土壤蒸发和作物蒸腾作用,只输入降雨数据,其中积水深度为蓄水层厚度(15 cm);下边界条件均选择渗漏面边界和自由出流边界。在模型率定过程中,可以对土壤水力特征参数和土壤初始含水率进行调整,以取得更好的率定效果。
由于此次降雨受前期降雨影响比较小,所以初始含水率设置在0.35左右。土壤水分特征曲线值以试验测量值为初始值进行率定。如表1所示。

表1 初始土壤水分特征参数表
2.1 初始含水率进行率定
由于基质的上表层含水率和下底层含水率有一定差别,首先对含水率的差值进行率定,此处选取六组模拟数据进行研究观察,模拟结果如图1所示。
由图1可知,当含水率介于0.32~0.36之间时(其平均含水率为0.34),与含水率介于0.25~0.43之间时候(平均含水率为0.34)模拟径流过程基本一致;同样,当上表面与下表面的平均含水率为0.345和0.35时,两组径流过程线也会重合。因此,可以看出基质上层含水率与下层含水率设置不同数值时,主要为平均含水率对模拟结果产生影响。

图1 初始含水率率定图
2.2 土壤水分特征参数敏感性分析
对于饱和含水率,取饱和含水率为0.54、0.548(试验值)和0.556进行分析,模拟结果如图2所示。

图2 饱和含水率敏感分析图
三种模拟值由小到大累计径流深对应值分别为13.1 mm、12.4 mm、11.7 mm,而实测值为4 mm。饱和含水率分别取了0.54、0.548(试验值)和0.556,差值为0.008,该差值对于峰值而言为敏感性参数。三者产流的起始过程线基本一致,在峰值附近的产流过程差异较大,当饱和含水率增大时产流峰值降低,产流速率减慢;当饱和含水率减小时,产流峰值增加,产流速率加快。当饱和含水率为0.54时模拟值与实际值较接近。
残留含水率差值为0.004径流过程线图,如图3所示。
三种模拟值由小到大累计径流深分别为13.1 mm、13.1 mm、13 mm,无太大变化。由图3可知,三种模拟值的过程基本重合,说明就差值0.004而言,对产流基本无影响。故增大差值进一步比较,此次选择差值0.01和0.03,模拟0.088和0.048两个产流过程,其结果如图4所示。

图3 残留含水率差值为0.004径流过程线图

图4 残留含水率差值为0.004、0.01、0.03产流过程对比图
以上五种模拟值只有当残留含水率为0.048时累计径流深变化最大,为13.4 mm。通过图4残留含水率差值分别为0.004、0.01、0.03产流过程对比图可知,过程线基本重合,残留含水率对降雨过程的产流并无有效影响,故以下的率定过程暂不予以考虑。
固定除饱和导水率之外的土壤水分参数值,选择初始值0.059(试验值),差值初定为0.005,即模拟0.049、0.054、0.059和0.064四个产流过程线。其结果如图5所示。

图5 饱和导水率差值为0.005产流过程对比图
四种模拟值由小到大累计径流深分别为12.5 mm、12.8 mm、13.1 mm、13.4 mm。由图5可知,饱和导水率对模型的产流时间以及初期、后期的产流过程有较小的影响,对峰值有一定的影响,饱和导水率变小,径流率最大值也随之变小,变化值为0.000 5 cm/min左右。饱和导水率越小,模拟值的总径流深越接近实测值。
四组模拟数据在峰值附近有小幅变化,但是不明显。由于此参数对该降雨模型有一定影响,故模拟差值初定为0.001产流过程进行比照分析。其过程对比如图6所示。

图6 α差值为0.001和0.005产流过程对比
α值为0.003 6~0.009 6时,累计径流深均为12.5 mm,可见α值对径流总量影响较小。由图6产流过程线可知,α值增大,峰现时间增长,体态变“胖”即产流稍微提前,峰值略有增加。
综上,通过参数的敏感性分析,做汇总表,结果如表2所示。

表2 人工改良土特征参数敏感性分析表
3 小结
通过HYDRUS-1D对绿色屋顶不同降雨条件的模拟,观察径流深、径流峰值及径流过程的变化,对不同参数下的降雨产流过程进行对比分析可以得出:
模拟参数中饱和含水率、N值对于绿色屋顶的径流特性影响最为明显,是决定产流时间和产流量的主要因素,是模拟精度提高的关键参数。残留含水率对各种雨强的模拟基本没有影响。
由于绿色屋顶的结构组成比较复杂,影响因素众多,模拟值与实测值有一定差值,本模拟只是产流过程线基本一致,这取决于模型的理论算法,有待于探索更合适的模型算法。
研究成果为海绵城市绿色屋顶降雨径流模型构建提供了针对性参考,为提高模型模拟精度提供技术支撑,后续其他海绵城市低影响开发措施降雨径流的模型构建、模拟及参数敏感性分析可参考本文的研究方法。

