基于神经网络的气象备件库存预测控制可用性研究

孟 超,刘 名,党 瑞,贺 易

（1.陕西省大气探测技术保障中心，陕西 西安 710014；2.渭南市气象局，陕西 渭南 714000；3.灞桥区气象局，陕西 西安 710014)

1 引言

为了有效地监控以及预测气象灾害，为社会发展提供保障，我国气象部门通过建设自动气象站等方式，提升对灾害性气象的预报预测能力。自动气象站指的是可以连续、自动地监测当地的风速、风向、温度、湿度、气压等气象资料的自动化气象设施[1]。包括气压仪器、雨量仪器、风向仪器、风速仪器、温度仪器、湿度仪器等设备，使用计算机系统实现设备的自动化运行，通过通信传输网络将监测数据传输给远程控制系统，提供气象管理、查询等功能[2]。设立气象备件库，以备气象设备出现故障，及时替换故障设备，保障自动化气象站的稳定运行，为国家和社会提供高质量的气象服务。备件库存过多，会占据过多的资金；备件库存过少，会容易出现自动气象站故障，无法及时更换影响气象观测业务运行。为此，如何预测控制气象备件库存至关重要，国内外相关学者对库存预测进行了研究。

刘金荣等[3]提出基于神经网络优化算法的库存预测应用研究，以历史库存为基础，分成训练集、验证集和测试集。结合遗传算法优化预测模型，利用测试集完成的模型预测结果，即未来一周的库存需求量。Chou[4]等人提出从前期需求和销售水平预测产品退货的库存模型的策略，将旧产品作为回购核心的回报率建模，分析了最优成本和最优策略的性质，得到了在过去销售的收益不可能被预测的模型下，最优库存策略的结构。

气象备件库存预测控制关键的环节是预测气象备件库存需求，国内外均对此进行了深入的研究，国内主要采用Bayesian方法预测气象备件库存需求，以此为基础，预测控制气象备件库存。国外主要采用回归分析法预测气象备件库存需求，预测控制气象备件库存。现有气象备件库存预测控制方法由于库存需求预测具有局限性，存在着数据拟合度低的缺陷，为了解决上述问题，提出基于神经网络的气象备件库存预测控制方法研究，并通过实验验证提出方法的可用性。

2 气象备件库存预测控制方法研究

2.1 BP 神经网络气象备件库存需求预测模型构建

气象备件库存需求预测是气象备件库存预测控制的关键环节，现有气象备件库存预测控制方法是以可修复备件管理多级法为依据预测气象备件库存需求，但由于此法计算过程繁琐，许多参数获取周期过长导致有极大的局限性，为此，此文利用BP 神经网络构建气象备件库存需求预测模型。

BP 神经网络是一种依据误差逆向传播进行算法训练的多层前馈网络，是现今使用最广泛的网络模型之一。BP神经网络由信息正向传播与误差逆向传播构成，结构为三层，分别为输入层、隐含层与输出层。其中，输入层神经元功能为接收与传播输入信号；隐含层是内部信息处理层，依据输入信号变化需求设置隐含层结构。若是单隐含层BP 神经网络，直接将信号传播给输出层，进行正向传播传递过程；若是多隐含层BP 神经网络，最后一个隐含层将信号传播给输出层，进行正向传播传递过程；输出层输出前两层处理信号。当输出值与期望输出值存在较大偏差时，返回进入误差逆向传播过程。输出误差以梯度下降方式更新各层的权值，逆向朝隐含层与输入层传播。

基于BP神经网络构建气象备件库存需求模型，构建步骤如下：

步骤一：输入层神经元指的是气象备件库存的影响因素。气象备件库存影响因素如表1所示。

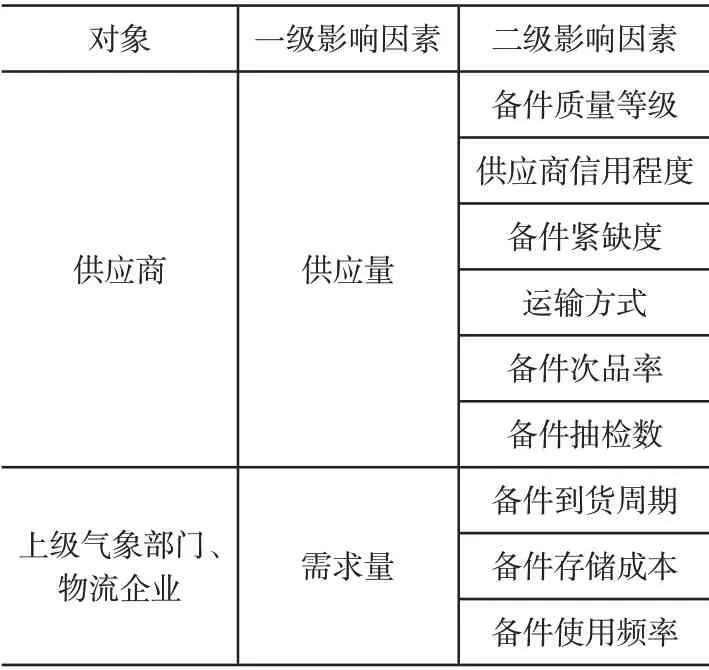
表1 气象备件库存影响因素表

为了简化构建模型的结构，筛选气象备件库存影响因素，将一级影响因素作为输入层的输入信号，则输入层神经元数量设置为2。此处神经元数量的设置参考文献[5]，引用神经网络建模得到的最优神经元数量值。

步骤二：采用二分分割法计算最佳隐含层节点数量。二分分割法流程如图1所示。

如图1流程所示，经过四轮实验，通过设置不同的隐含层节点数量，得到对应的误差值，最后通过二分分割法得到隐含层节点数量为6。

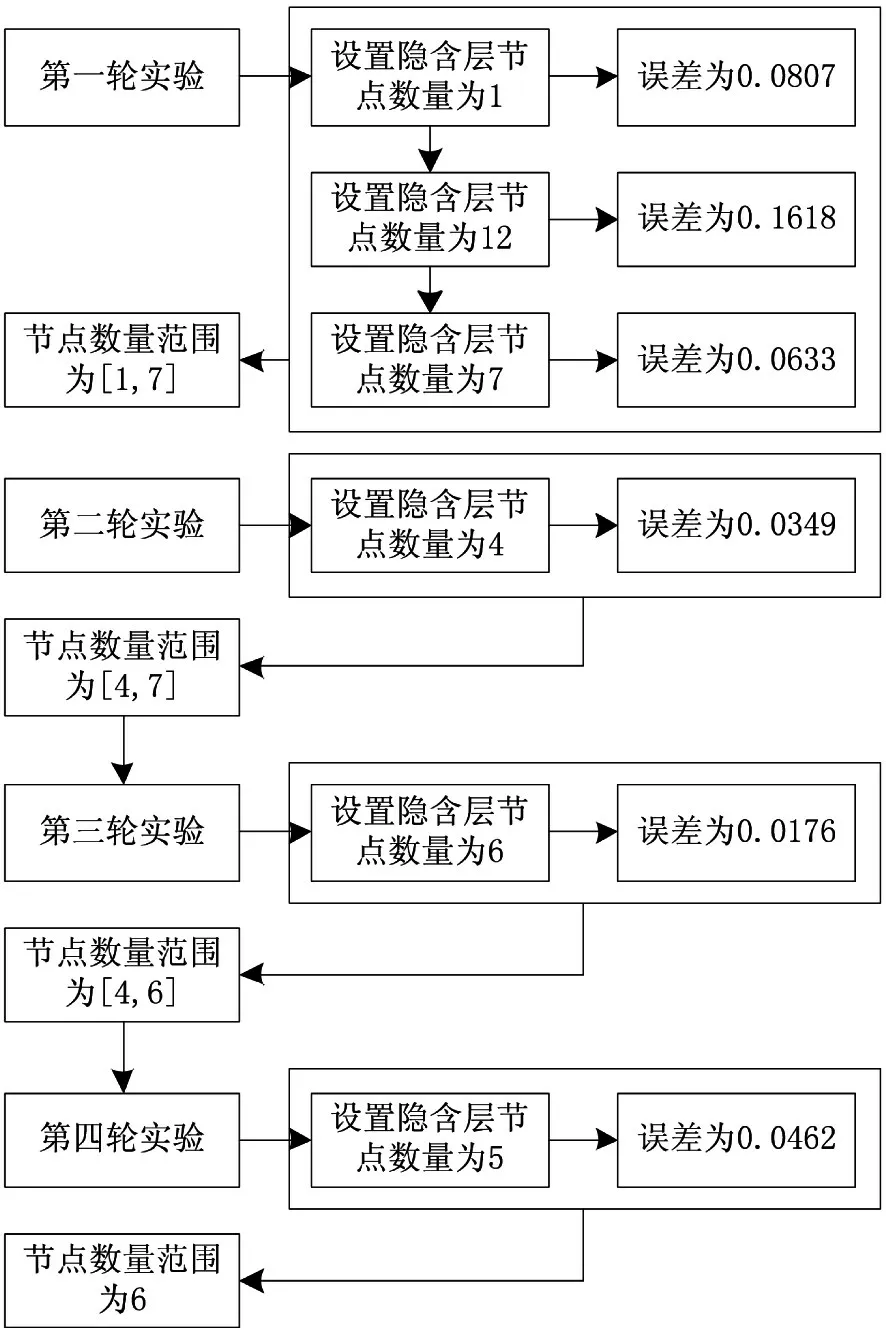
图1 二分分割法隐含层节点数量确定流程图

步骤三：输出层神经元是气象备件库存需求预测值，神经元数量设置为1。

2.2 模型输入数据非线性关系拟合

BP 神经网络气象备件库存需求预测模型精度会受到多种因素的影响，如何选择与处理模型输入数据成为模型应用的关键难题。此节拟合模型输入数据非线性关系，计算输入数据的非线性相关系数，以此为基础，选择输入数据。此处参考了文献[6]中预测模型的构建过程，考虑了预测过程中干扰因素较多的情况，为保证输入数据的贴合性，计算其非线性相关系数。

已知气象备件库存输入数据具有非线性相关特征[7-9]，设定输入数据为y(t)，离散形式为y(n)，其非线性相关函数为：

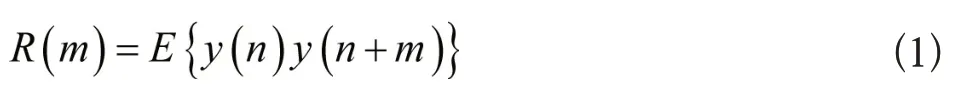
式(1)中，R(m)表示的是输入数据的非线性相关函数；m表示的是输入数据的数量。

通过拟合得到输入数据非线性相关函数集总平均为：

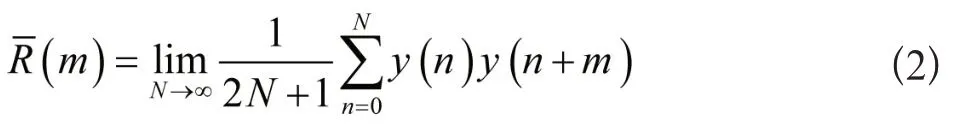
式(2)中，R(m)表示的是输入数据非线性相关函数集总平均值；N表示的是y(n)的观测值数量。

对于每一个固定的延迟|m|，可以利用的输入数据数量为N-1-|m|，则拟合输入数据非线性关系表示为：

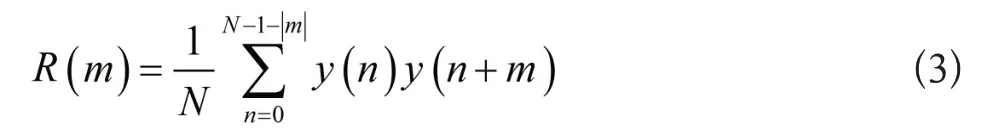
式(3)中，R(m)表示的是拟合输入数据非线性关系函数。

将公式(3)进行归一化处理，得到表达式为：

式(4)中，η(m)表示的是归一化拟合输入数据非线性关系函数形式；R(0)表示的是输入数据单位非线性相关系数。

输入数据非线性相关系数计算公式为：

通过上述过程得到输入数据非线性关系拟合情况如图2所示。

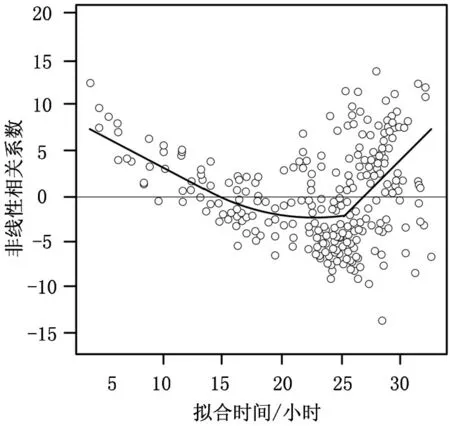
图2 输入数据非线性关系拟合图

如图2所示，由于气象备件库存需要考虑的因素较多，为进一步排除干扰因素，上述计算将非线性相关系数大于0.75的数据，作为BP神经网络气象备件库存需求预测模型的输入数据，以此来提升模型预测精度。

2.3 气象备件库存预测控制

以气象备件库存数据为基础，输入到构建的BP神经网络气象备件库存需求预测模型中，得到气象备件库存需求量，依据协方差(Covariance，COV)分析法计算气象备件消耗数量，分类气象备件，以此为基础，选取不同的预测控制方法，实现以基于BP神经网络的气象备件库存的预测控制。

COV分析法主要是依据新型自动气象站以往的备品备件消耗数量，计算标准偏差值与平均值，而COV.就是标准偏差值与平均值的商值[10-11]。计算公式为：

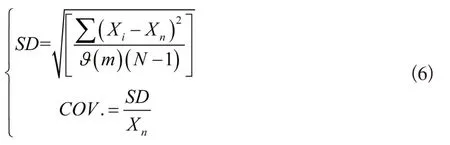
式(6)中，SD表示的是标准偏差值；Xi表示的是第i个样本值；Xn表示的是样本X的算术平均值；N表示的是样本个数。依据公式(6)的计算结果分类气象备件，为气象备件库存预测控制方法选取做准备，具体气象备件分类情况如表2所示。

表2 气象备件分类表

气象备件的重要等级是存在较大的不同，对其库存预测控制的方式也相应不同，为此，利用帕累托分类法(Activity Based Classification，ABC)，通过打分排序气象备件重要等级。

ABC分类法判断指标与分值，如表3所示。

表3 ABC分类法判断指标与分值表

ABC分类法气象备件重要等级划分规则如表4所示。

表4 气象备件重要等级划分规则表

气象备件九宫格分类依据如表5所示。

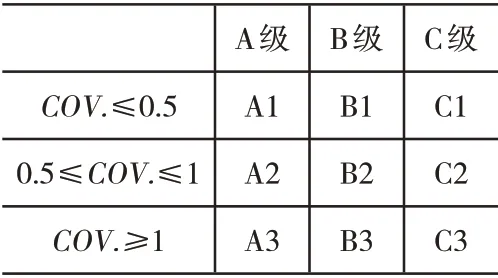
表5 气象备件九宫格分类依据表

依据表5分类情况分别选择气象备件库存预测控制方法。其中，A1、A2、B1、B2 型气象备件选取最小-最大值法预测控制库存，该方法要求库存管理人员实时监测气象备件库存水平，当上述类型气象备件库存量下降到最小值时，对其进行补充，补充值为预测最大值减去安全库存的差值；

C1、C2 型气象备件选取EOQ 批量法预测控制库存，该方法指的是当上述类型库存量下降至订货点时，依据批量规则进行订货；

A3、B3、C3 型气象备件选取按需求计划订货方法预测控制库存。对于A3、B3、C3型气象备件来说，其COV.值大于等于1，其需求量很难预测，因此，最科学的预测控制方法即按照需求计划进行订货，并严格执行使用计划。该方法不会导致气象备件严重缺货，也不会造成气象备件积压过多。

上述过程实现了基于BP神经网络的气象备件库存预测控制方法的设计，通过气象备件库存预测控制方法的选择，为自动化气象站制定合理采购计划提供良好的建议。

3 可用性测试研究

为了验证设计的基于BP 神经网络的气象备件库存预测控制方法的可用性，设计仿真对比测试，具体测试过程如下所示。

3.1 实验环境构建

测试采用MATLAB 仿真平台进行，利用MATLAB神经网络工具箱中的神经网络设计与训练函数，并对其依据实际情况改进，部分使用到的BP神经网络设计与仿真函数如表6所示。

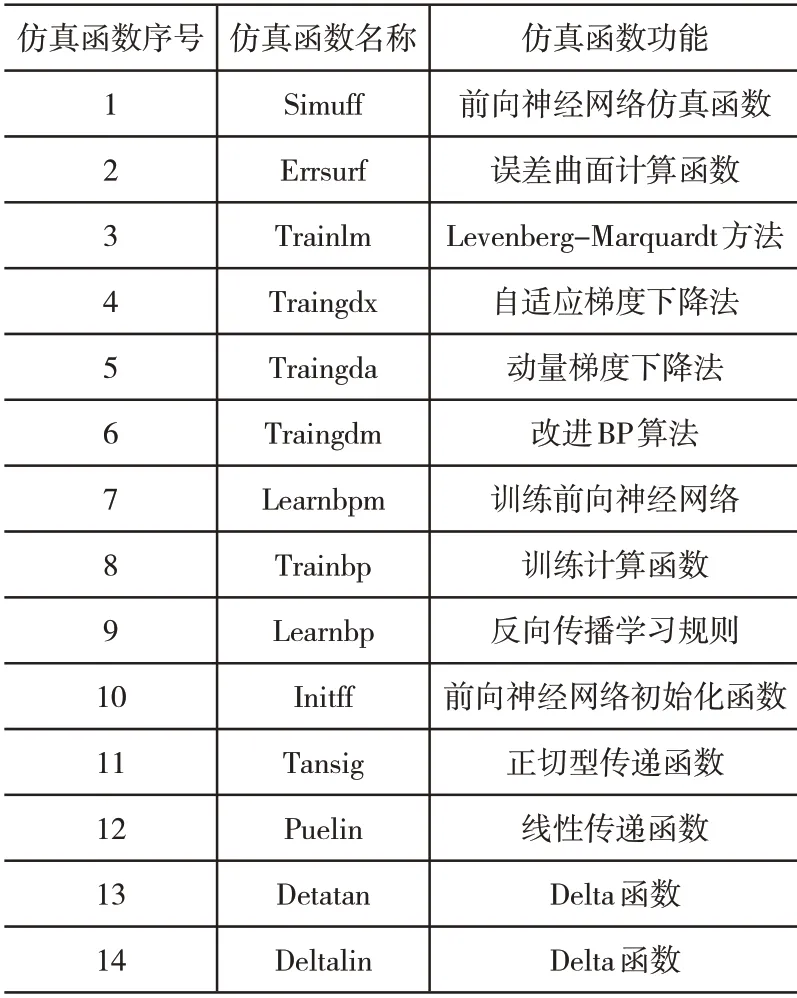
表6 部分BP神经网络仿真函数表

3.2 BP神经网络结构确定

BP神经网络结构需要测试与训练，其流程如图3所示。

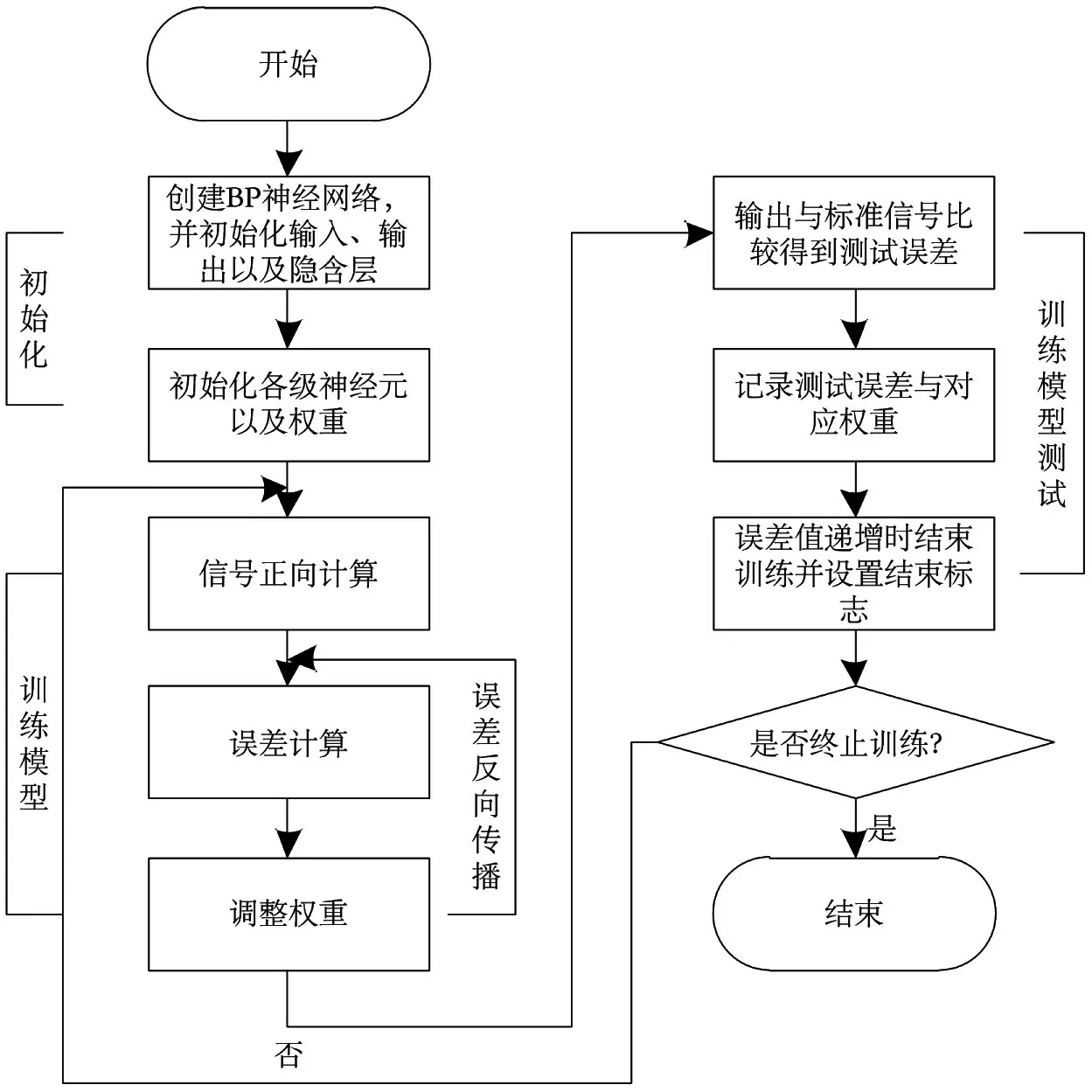
图3 BP神经网络结构测试、训练流程图

如图3所示，BP神经网络结构训练方案如表7所示。

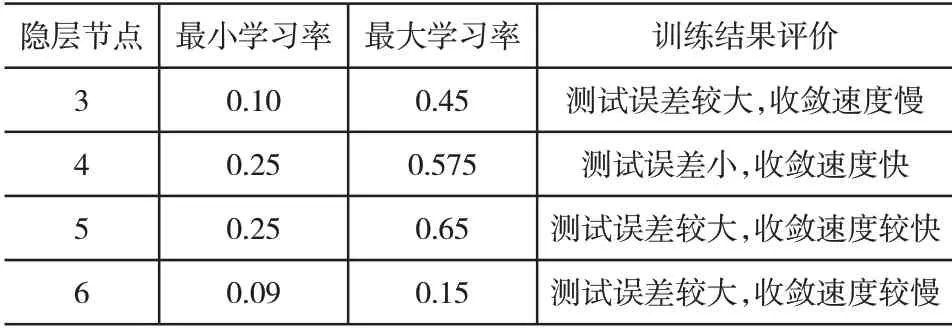
表7 BP神经网络结构训练方案表

BP神经网络结构需要进行自动调整，以此来满足测试的需求，隐节点调整前、后相关系数与发散度情况如表8与表9所示。

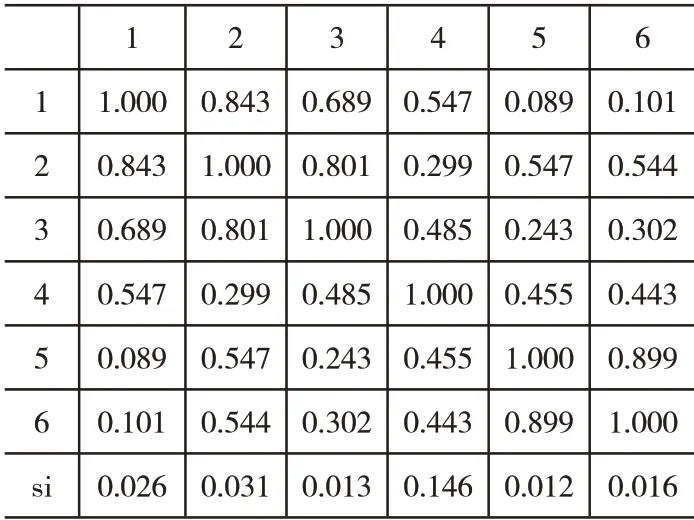
表9 隐节点调整后相关系数与发散度表

如表8与表9所示，隐节点0与1相关性较大，合并处理，则隐节点为6个，确定了BP神经网络的结构，为仿真对比测试做准备。

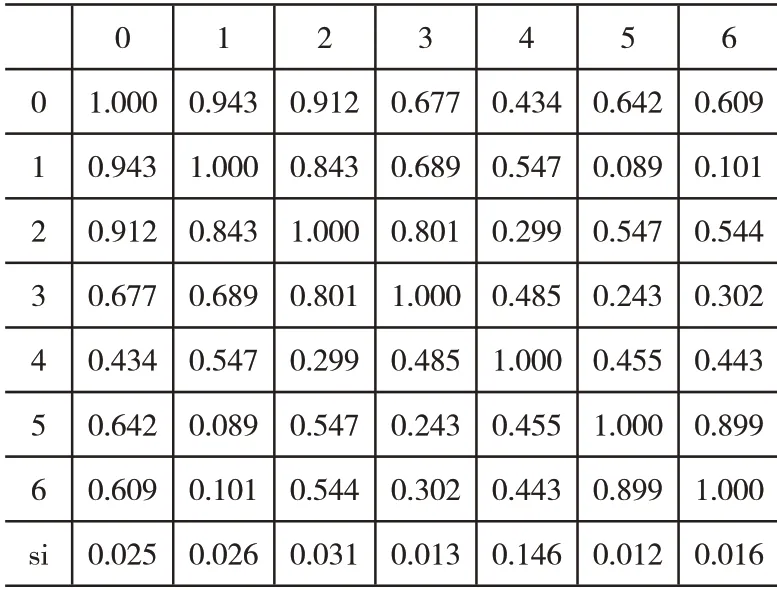
表8 隐节点调整前相关系数与发散度表

3.3 神经网络训练

将测试样本集输入BP神经网络中，通过正向传播与反向权值调整，该过程称为一次训练，经过12次迭代得到收敛曲线如图4所示。

图4 神经网络训练收敛曲线图

由图4所示，神经网络训练收敛速度较快，误差较小。

3.4 测试结果分析

气象备件库存预测控制方法的可用性采用数据拟合度来表示，通过测试得到数据拟合度对比情况如表10所示。

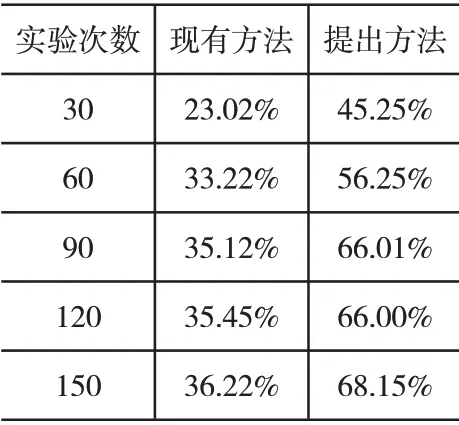
表10 数据拟合度对比情况表

如表10数据显示，提出方法的数据拟合度远高于现有方法，表明提出方法具备更好的可用性。

4 结束语

此文提出的基于神经网络的气象备件库存预测控制方法极大地提升了数据拟合度，具备更好的可用性，可以为自动化气象站制定合理采购计划提供良好的建议。但是未将计算时间等因素考虑在内，因此，需要对提出的基于神经网络的气象备件库存预测控制方法进行进一步的优化研究。