考虑洪水地区组成不确定性的水库下游防洪风险率计算

孙乃波, 刘克琳， 程亮， 杜慧华

(1.威海市水文中心，山东 威海 264209； 2.南京水利科学研究院 水文水资源与水利工程科学国家重点实验室，江苏 南京 210029)

随着对江河的治理与开发，水库群的调节对下游防洪控制点洪水过程的影响愈来愈突出[1]。水库群的削峰和滞洪作用，一般会使得控制点洪水洪峰减小，峰现时间后移，与天然条件下的洪水过程有较大差异。洪水过程变化导致控制点防洪风险率变化，科学评估水库群调节作用下控制点的防洪风险率，对复核流域防洪标准、优化水库群防洪调度规则具有重要意义[2]。

当只考虑洪水不确定性时，控制点防洪风险率可用一定时间内控制点洪水流量超过河道安全泄量的概率来表示。因此，如何用概率描述水库群调节作用下控制点的洪水过程，是评估防洪风险率的核心。设计洪水在概念上具有概率属性，是洪水概率描述的一种常用方式。根据《水利水电工程设计洪水计算规范》(SL 44—2006)，探寻水库群调节影响下防洪控制点设计洪水的方法，目前主要有地区组成法、频率组合法[3]和随机模拟法[4]。其中地区组成方法是规划设计中最常采用的方法，包括典型洪水组成法和同频率洪水组成法。近些年，有学者基于Copula函数提出条件期望组成和最可能组成[5]，或采用当量正态化(JC)法拟定一种最不利的地区组成[6-7]，这些方法都是对地区组成法的改进。

由于洪水在空间分布上存在不确定性，当控制点发生一定频率洪水时，其上游水库和区间洪水可能存在多种组成方式，或者说每一种地区组成都是一个概率事件[8]。地区组成法采用单一洪水地区组成，或者从多个地区组成中选择一个最不利的地区组成，这对洪水地区组成的不确定性考虑不足。洪水地区组成法尽管在主观上考虑对防洪不利的原则，但客观上却使防洪断面不满足预定的防洪标准[9]。频率组合法和随机模拟法虽然考虑了水库与区间洪水的所有可能组成方式，但计算过程中没有采用控制点天然洪水的概率分布，从而失去了与天然设计洪水以及地区组成法对比的基础。

为此，本文结合地区组成法和频率组合法的思路，以单库防洪系统为对象，提出计算水库下游控制点防洪风险率的离散求和-均值一次二阶矩法(discretization summation-mean first order second moment method, DS-MFOSM)。该方法根据水库和区间洪量的二维联合分布函数推导某一设计频率下洪水地区组成的概率密度函数，用以描述洪水地区组成的不确定性；通过引入水库调洪函数和洪水峰量关系函数，采用均值一次二阶矩法计算控制点组合洪峰流量在某一设计频率下超过安全泄量的概率；最后，采用离散求和得到控制点的防洪风险率。该方法不仅考虑了洪水地区组成的不确定性，还能描述该不确定性在防洪系统中的传递特征。最后，以沭河流域的沙沟-青峰岭防洪系统为实例，将该方法进行了应用。

1 基本原理与方法

单库防洪系统如图1所示，水库A、区间和防洪控制点的天然洪量分别用随机变量X、Y和Z表示,水库下泄流量用qA表示。防洪控制点洪峰流量频率曲线如图2所示，图2中线1为天然洪峰流量的频率曲线，线2为在某一洪水地区组成下水库调洪影响后洪峰流量的频率曲线。传统的地区组成法、频率组合法和随机模拟法都能得到一条确定的线2，进而根据线2和安全泄量得到控制点的防洪风险率。由于洪水地区组成具有不确定性，对于某一设计频率pi，水库调洪影响后防洪控制点的组合洪峰流量不是一个确定值，而是一个随机变量，这是本文与传统方法的主要区别所在。

图1 单库防洪系统示意图

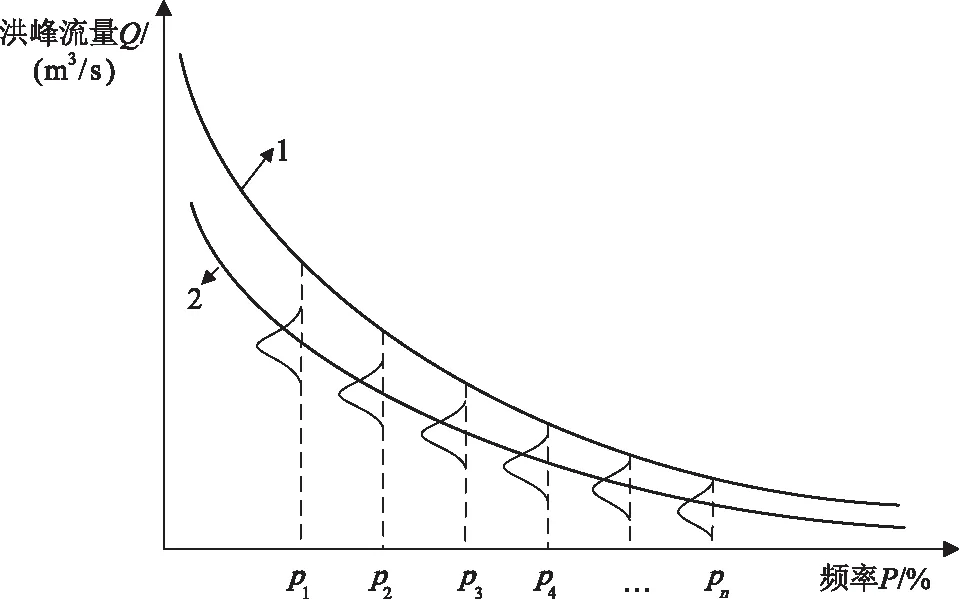
图2 防洪控制点洪峰流量-频率曲线图

假定随机变量X、Y和Z的取值分别为x、y和z。防洪控制点设计频率pi的天然洪量设计值为zpi，根据洪水地区组成的原理，存在以下关系式：

x+y=zpi，x≥0，y≥0。

(1)

随机变量X、Y一般服从P-Ⅲ型分布，其概率密度函数分别为：

(2)

(3)

式中αx、βx、γx和αy、βy、γy分别为随机变量X和Y的P-Ⅲ型分布的参数。

X、Y的概率密度分布函数分别表示为FX(x)、FY(y)，其联合分布函数可用二维Copula函数表示：

FX,Y(x,y)=Cθ(u,v)=Cθ(FX(x),FY(y))。

(4)

对应的二维概率密度函数表示为：

fX,Y(x,y)=cθ(FX(x),FY(y))fX(x)fY(y)。

(5)

根据式(1)和式(5)，洪水地区组成(x，zpi-x)的概率分布可用归一化的条件概率密度函数g(x)进行描述，其表达式为[8]：

(6)

引入水库调洪函数h(x)，依据水库调洪规则，通过拟合水库最大下泄流量h(x)与入库洪量x的关系获得调洪函数。对于下游有防洪任务的水库而言，调洪函数一般为分段函数。此外，建立区间洪峰流量与洪量关系函数u(y)，可通过拟合区间洪峰流量u(y)与区间洪量y的散点系列得到峰量关系函数。

设防洪控制点的安全流量为qan，假定水库下泄洪峰与区间洪峰在控制点相遇，则设计频率为pi时的防洪控制点洪峰流量超过安全泄量的概率Pfi为：

Pfi=P(h(x)+u(zpi-x)>qan)。

(7)

采用均值一次二阶矩法求解式(7)，并建立功能函数w(x)：

w(x)=qan-h(x)-u(zpi-x)。

(8)

将功能函数w(x)在均值点μx处展开为泰勒级数并保留至一次项，得到：

w(x)=w(μx)+w′(μx)(x-μx)。

(9)

式中w′(x)为w(x)对x的导数。

根据式(8)和式(9)，统计w(x)的均值μw和均方差σw，计算式分别如下：

μw=w(μx)=qan-h(μx)-u(zpi-μx)，

(10)

σw=w′(μx)σx=(1-h′(μx)+u′(zpi-μx))σx。

(11)

式中：h′(x)为h(x)对x的导数；u′(x)为u(x)对x的导数。

式(11)描述了洪水地区组成不确定性通过方差在防洪系统中的传递过程。Pfi可由下式估算：

(12)

式中Φ(x)为标准正态分布函数；μx、σx分别根据式(6)提供的条件概率密度函数g(x)得到：

(13)

(14)

由式(13)和(14)一般无法获取解析解，可采用数值积分法得到数值解。

根据离散求和法的思想，在频率曲线的横坐标上选择n个典型频率值，从小到大排序分别为pi(i=1、2、…、n)，以此为中心把整个频率的0～1区间划分成n个小区间，每个小区间的概率为：

(15)

水库下游控制点的防洪风险率Pf估算式为：

(16)

2 计算流程

离散求和-均值一次二阶矩法(DS-MFOSM)计算水库下游控制点防洪风险率的流程如图3所示，具体如下：

图3 离散求和-均值一次二阶矩法计算流程图

1)根据水库和区间洪量系列计算边缘分布函数FX(x)、FY(y)和概率密度函数fX(x)、fY(y)；

2)利用二维Copula函数构造水库和区间洪量的联合分布函数FX,Y(x,y)和概率密度函数fX,Y(x,y)；

3)将控制点天然洪量在频率曲线图上进行离散，得到pi，利用式(15)计算Δpi，并在频率曲线上查找zpi；

4)对于任一个zpi，采用数值计算的方法，根据式(6)计算地区组成的概率密度函数g(x)，再根据式(13)、(14)计算其均值μx和均方差σx；

5)构建水库调洪函数h(x)和区间洪水峰量关系函数u(y)，分别推导其导数函数h′(x)、u′(y)；

6)确定控制点安全流量qan，根据式(12)计算设计频率为pi的风险率Pfi；

7)根据式(16)计算水库下游控制点的防洪风险率Pf。

3 实例应用

以沭河流域的沙沟-青峰岭防洪系统作为应用实例。沙沟水库位于沂沭河水系沭河干流的上游，控制流域面积163 km2，总库容1.02亿m2，汛限水位234 m，百年一遇设计洪水位237.32 m，千年一遇校核洪水位239.30 m。沙沟水库防洪调度规则是20年一遇洪水控泄500 m3/s，超过20年一遇洪水水库敞泄，水库下游38 km处的青峰岭水库为沙沟水库的下游防洪控制点。

防洪系统各分区设计洪水历时均为3 d，因此选择最大3 d洪量作为洪水地区组成的特征量，其天然设计成果见表1,表中Cv、Cs分别为变差系数和偏态系数。

表1 各分区最大3 d洪量天然设计成果

利用1964—2011年沙沟水库和沙沟-青峰岭区间(沙青区间)最大3 d洪量统计系列，采用Gumbel-Hougaard Copula函数构造二维联合分布函数，参数θ估计值为3.125，分布函数如图4所示。

图4 水库与区间3 d洪量联合分布函数图

根据沙沟水库调洪规则和设计洪水成果，构造沙沟水库调洪函数：

(17)

根据1964—2011年沙青区间的洪峰流量与年最大3 d洪量系列，构造洪水峰量与洪量关系函数：

u(y)=22.779y-61.757。

(18)

选择沙沟水库防洪标准对应的设计频率5%，根据表1，该频率下青峰岭天然设计3 d洪量z5%=115.20×106m3，青峰岭安全泄量为2 500 m3/s。根据式(6)计算出设计频率为5%的地区组成概率密度函数g(x)，如图5所示，根据数值积分法计算出该概率密度函数的均值为34.31×106m3，均方差为8.68×106m3。

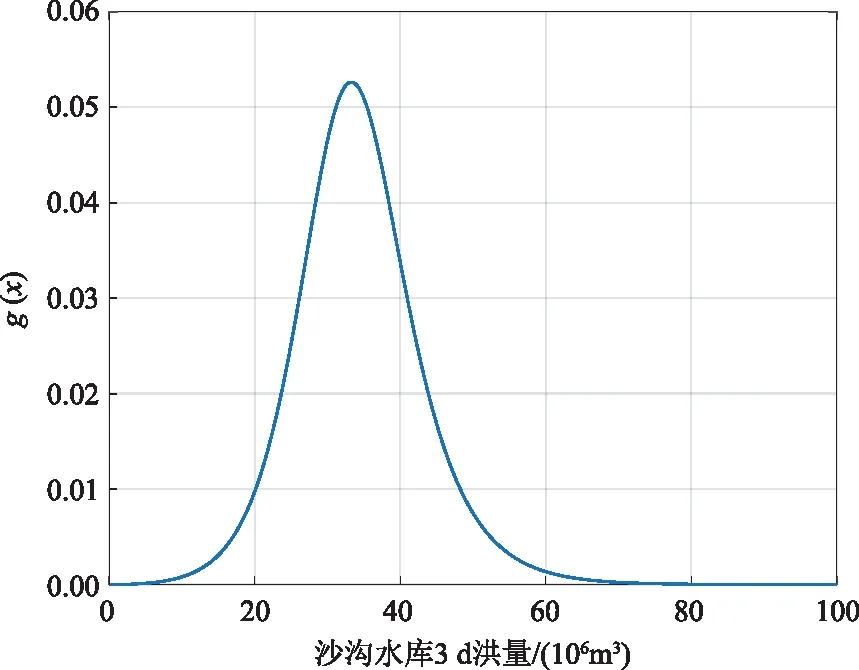
图5 设计频率为5%的地区组成密度函数图

将0～1区间频率进行离散，在防洪标准频率附近适当加密，计算青峰岭断面各设计频率下的防洪风险率及总的防洪风险率，结果见表2。

表2 青峰岭断面防洪风险率计算结果

将表2中最后一行数据相加可得，青峰岭断面的防洪风险率为4.02%，小于沙沟水库防洪标准频率5%，表明在现行的沙沟水库防洪调度规则下，沙沟-青峰岭防洪系统满足防洪标准要求。

图6为青峰岭断面设计频率pi与风险率Pfi相关图。从图6中可知，随着设计频率pi的增大，设计洪水变小，设计频率下pi的风险率Pfi随之减小。

图6 青峰岭断面设计频率pi与风险率Pfi相关图

4 结论

以单库防洪系统为研究对象，提出了计算水库下游控制点防洪风险率的离散求和-均值一次二阶矩法，该方法以某一设计频率下的地区组成概率密度函数描述洪水地区组成的不确定性，结合水库调洪函数和洪水峰量与3 d洪量关系函数，采用均值一次二阶矩法计算某一设计频率下的控制点洪峰流量超过安全流量的概率，进而采用离散求和法计算控制点总的防洪风险率。最后将该方法应用于沭河的沙沟水库-青峰岭断面防洪系统。主要结论有：

1)离散求和-均值一次二阶矩法既采用了地区组成法中的先分配、再组合的思路，又考虑了设计洪水地区组成的不确定性，并且能够描述该不确定性在水库防洪系统中的传递特征。

2)实例应用表明，在沙沟水库防洪调度规则下，沙沟-青峰岭防洪系统满足防洪标准要求。

3)离散求和-均值一次二阶矩法给出了计算防洪风险率的解析式，但受限于联合分布函数的维数，该方法仅适用于包含区间洪水的单库防洪系统。