考虑参数-激励复合随机的渡槽结构非线性地震响应与抗震可靠性分析

张威 孙振华 王博 徐建国

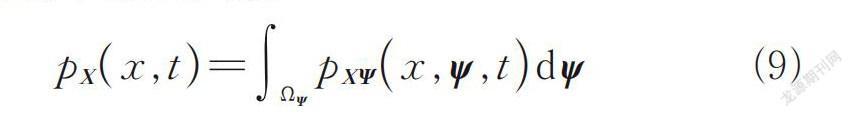
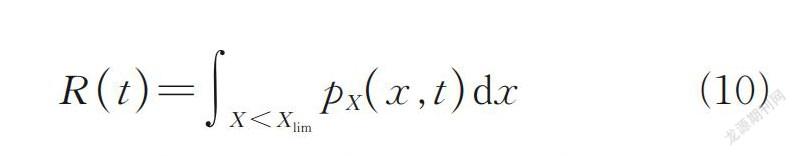
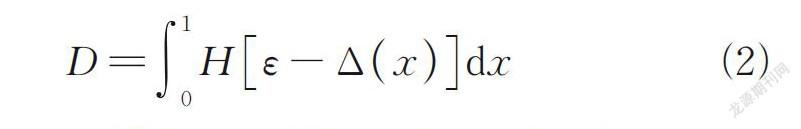
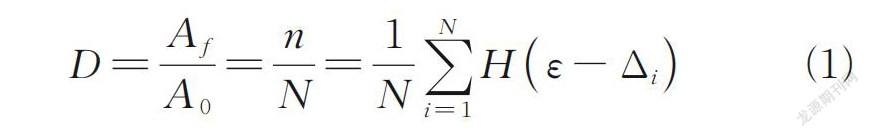
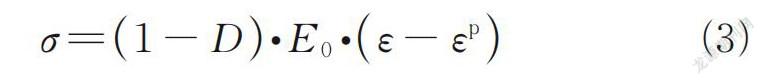
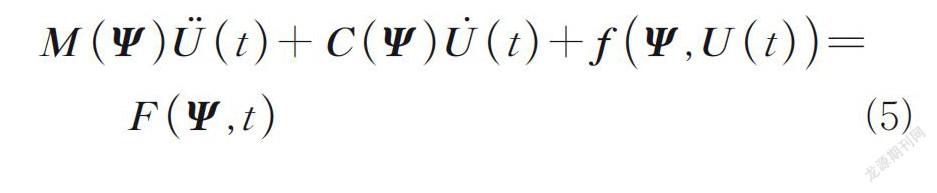
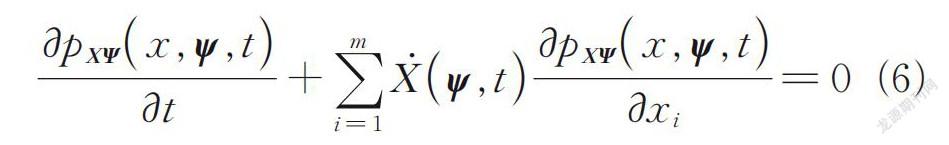
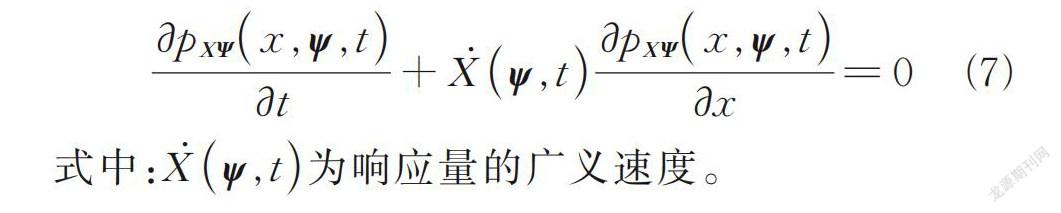
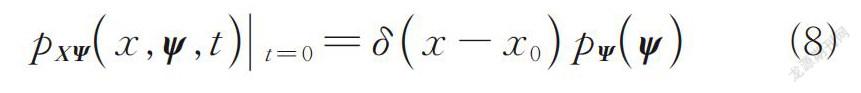
摘要：地震灾害对渡槽结构的破坏受多种因素的影响和制约，混凝土力学参数的随机性和地震激励的随机性为两种较为重要的影响因素，会对渡槽结构的破坏模式产生显著影响。进行混凝土力学参数和地震激励两种随机性耦合作用下的渡槽结构随机动力响应分析，以某大型渡槽结构为例，提出考虑参数—激励复合随机的渡槽结构抗震可靠性分析方法。基于概率密度演化理论，该方法阐明了渡槽结构在复合随机作用下可靠性分析的基本原理和应用途径。与单一地震随机作用的比较研究发现，复合随机作用下渡槽结构的位移响应明显加剧，且位移响应产生的残余变形和位移的变异性较大；随着阈值的减小，渡槽结构在复合随机作用下的可靠度与单一随机地震作用下的可靠度之间的差距呈不断增大趋势，且渡槽结构在两种工况下的可靠度均不断减小。

关键词：渡槽结构；抗震可靠性；复合随机；概率密度演化理论；抗震分析

中图分类号：TV312；TV672 文献标志码：A 文章编号：2096-6717（2022）06-0144-09

Nonlinear seismic response and reliability analysis of aqueducts subjected to coupled randomness from structural parameters and excitations

ZHANG Wei 1，SUN Zhenhua 2，WANG Bo 3，XU Jianguo 3

（1.School of Engineering Management and Real Estate，Henan University of Economics and Law，Zhengzhou450046，P.R.China；2.Henan College of Transportation，Zhengzhou 450000，P.R.China；3.School of Water Conservancy and Civil Engineering，Zhengzhou University，Zhengzhou 450001，P.R.China）

Abstract：The damage of aqueduct structures caused by earthquake disaster is influenced and restricted by various factors.The randomness in concrete mechanical properties and seismic excitations are two of the significant factors that may alter the failure modes of aqueduct structures.To this end，this paper carried out systematically the random dynamic response analysis of aqueducts subjected to the above two coupled randomness condition.Further，the anti-seismic reliability analysis method for aqueducts considering the coupled randomness from both structural parameters and excitations is developed taking alarge aqueduct structure as an example.The basic research principles and application approaches of the developed framework were illustrated in detail based on the probability density evolution theory.The results show that the displacement response of the aqueduct structure under the coupled randomness condition intensifies obviously，and the residual deformation and displacement variability of the displacement response are larger than that caused by the single randomness earthquake condition.With the decrease of threshold value，the gap between the reliability of aqueduct structure under coupled randomness condition and that under single randomness earthquake condition is increasing，and the reliability of aqueduct structure under the above two conditions is decreasing continuously.

Keywords：aqueduct structure；anti-seismic reliability；coupled randomness；probability density evolution theory；seismic analysis

中國修建了南水北调中线工程等若干跨流域调水工程，把水资源丰富地区的富余水量跨流域调配到水资源短缺地区，弥补了受水区的用水短缺，在一定程度上缓解了中国水资源地域分布不均的现状。大型渡槽结构是跨流域调水中不可或缺的输水建筑物，且不少渡槽结构处在地震高烈度区。在灾害性地震作用下，渡槽结构易发生损伤或破坏，甚至会导致正常的输水过程中断。因此，开展渡槽结构的地震响应分析与抗震可靠性研究具有重要的现实意义。

近年来，相关学者开展了渡槽结构抗震可靠性方面的研究。安旭文等[1]借助有限单元法和蒙特卡洛方法，开展了渡槽结构的抗震可靠性研究。刘章军等[2]采用正交多项式展开对某渡槽开展了随机地震响应与抗震可靠性分析。Ma等[3]建立了基于主失效模式和综合相关系数法的渡槽系统可靠性分析模型，深入研究了洺河渡槽桩梁多侧壁的系统可靠性。然而，以上渡槽结构可靠性研究多是基于随机模拟方法，计算效率较低。张多新等[4]系统总结了近十年来渡槽结构动力学研究进展，指出基于工程结构的动力学可靠度理论已在渡槽工程中开展研究，并渐露曙光。张威等[5]从动力可靠度理论出发，开展了随机性地震动激励下的渡槽结构非线性动力响应分析和可靠性研究，发现地震激励的随机性会对渡槽结构的非线性动力响应规律产生显著影响。张威等[6]从材料参数随机性出发，在考虑混凝土力学参数随机性的条件下，开展了渡槽结构的地震响应分析，给出了渡槽结构输水功能可靠性分析方法。然而，上述渡槽结构可靠性研究仅考虑了一种随机因素。事实上，渡槽结构遭遇地震破坏时，不仅受地震激励随机性的影响，还受混凝土力学参数随机性的影响。已有文献研究表明[7]，在强动力非线性的作用下，混凝土力学性能的随机性会对建筑结构地震响应造成重大影响。因此，更有必要对“头重脚轻”的渡槽结构开展考虑地震激励随机性和混凝土力学性能随机性的地震响应和可靠性分析，以更客观地反映渡槽结构在遭遇地震作用时的响应规律和抗震可靠性。

为充分考虑渡槽结构在灾害性地震作用下的响应特性，采用混凝土随机损伤力学模型[8]反映渡槽结构在动力荷载作用下的随机性与非线性性能[6]。近年来，概率密度演化理论体系为工程结构系统可靠性问题的解决开辟了有效路径[9-10]。与传统随机模拟方法相比，概率密度演化方法从理论和实践上解决了可靠性分析中随机耦合问题带来的困难，被成功用于上海中心、上海广电中心等超高层建筑结构的抗震可靠性评估[11-12]。基于此，笔者将考虑参数—激励复合随机因素，开展渡槽结构的非线性动力响应分析，并援引概率密度演化方法研究其在复杂因素作用下的动力响应规律和抗震可靠性。

1 渡槽结构模型

为了研究渡槽结构在复合随机下的地震响应规律与抗震可靠性，以某大型渡槽结构为例，基于OpenSEES分析平台建立了大型渡槽结构有限元分析模型。

1.1 渡槽结构有限元分析模型

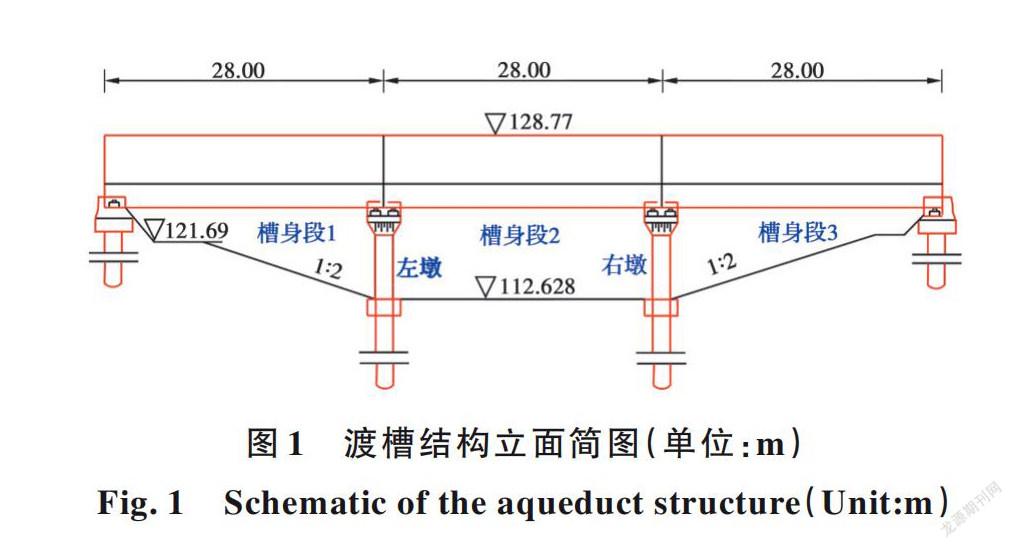
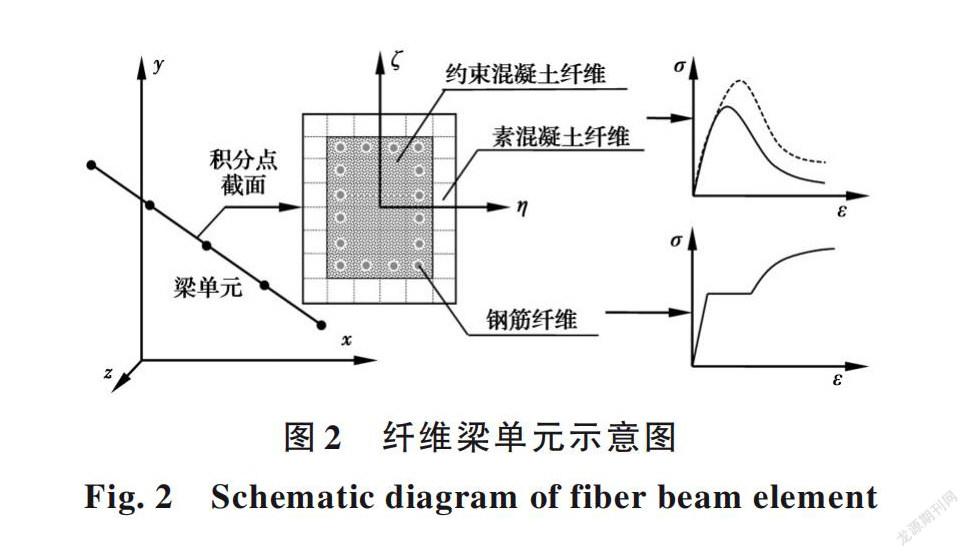
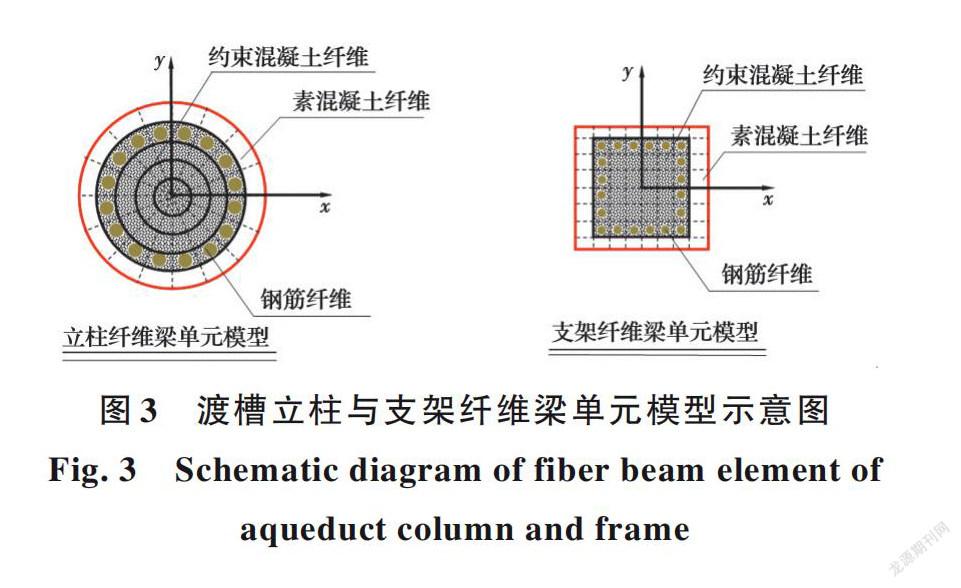
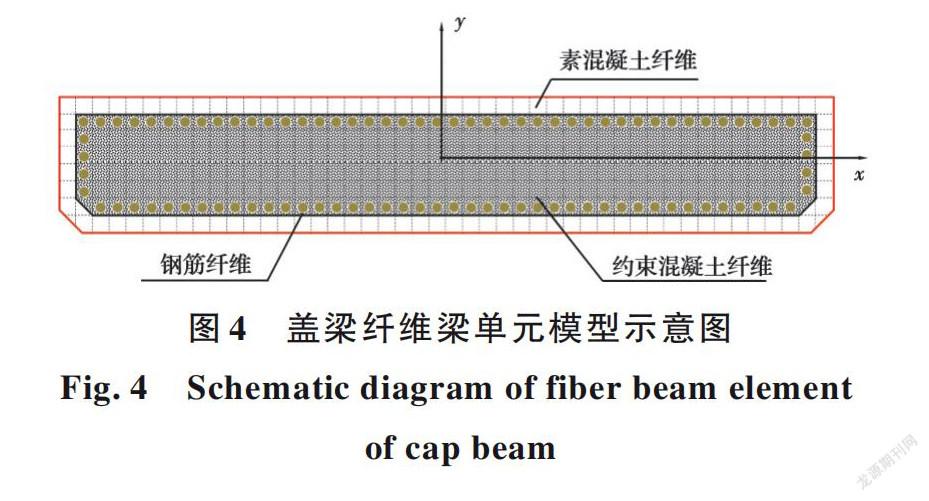
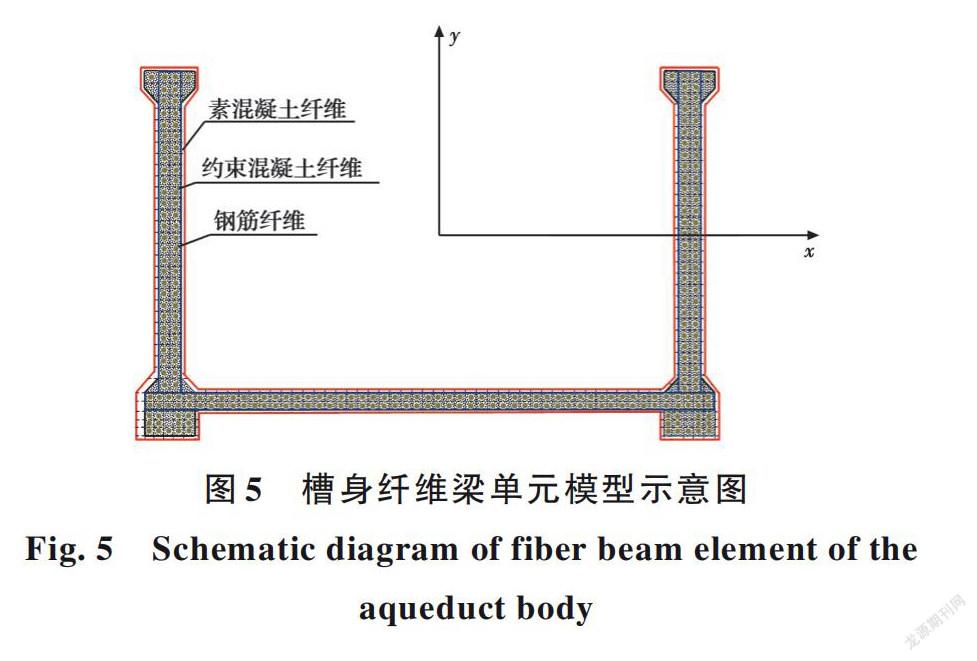
南水北调中线工程某大型渡槽结构[5]如图1所示。该渡槽结构所处场地类型为二类场地，抗震设防烈度7度，设计基本地震加速度值为0.10g，设计地震分组为二组。渡槽墩底部与地基固结，盆式橡胶支座设置于渡槽墩顶部。槽内设计水深2.21 m，采用附加质量法将水体固结于槽身。利用开放性有限元开发平台OpenSEES[13-14]建立渡槽结构有限元模型。该模型采用纤维梁单元，槽身处积分点数量设置为5，盖梁、槽墩处积分点数量设置为3；依据力学原理定义截面属性，如图2所示。为了清晰表达渡槽结构不同部位的纤维梁单元，给出渡槽结构在立柱与支架、盖梁和槽身的纤维梁单元模型示意图，如图3～图5所示。

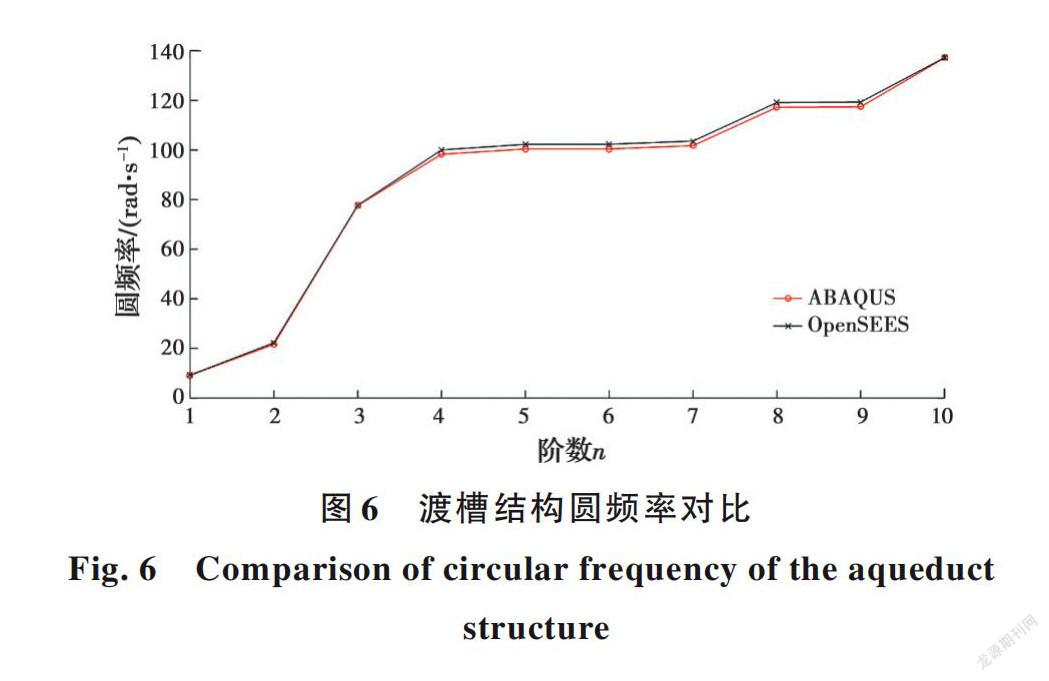
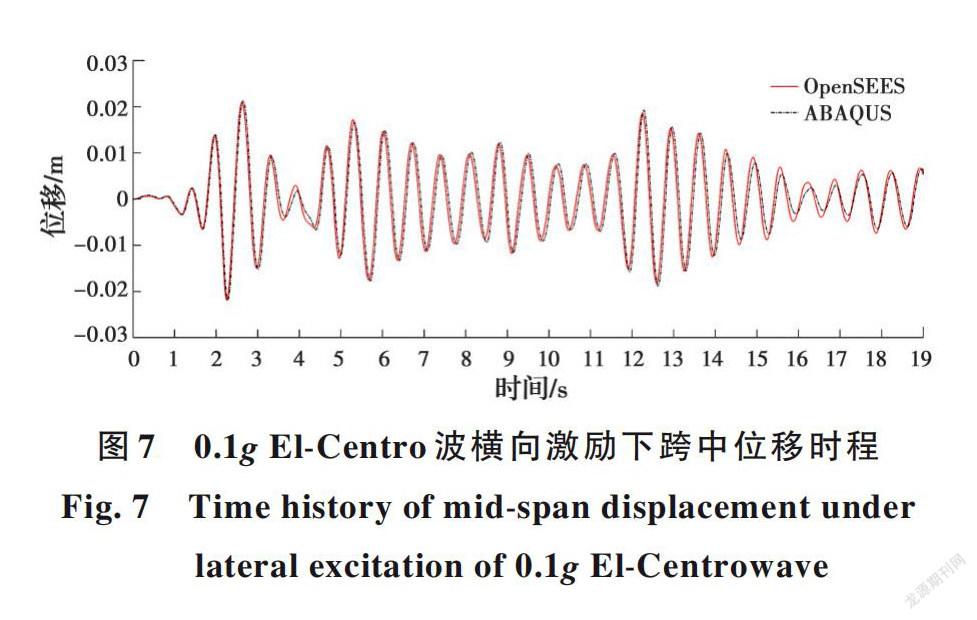
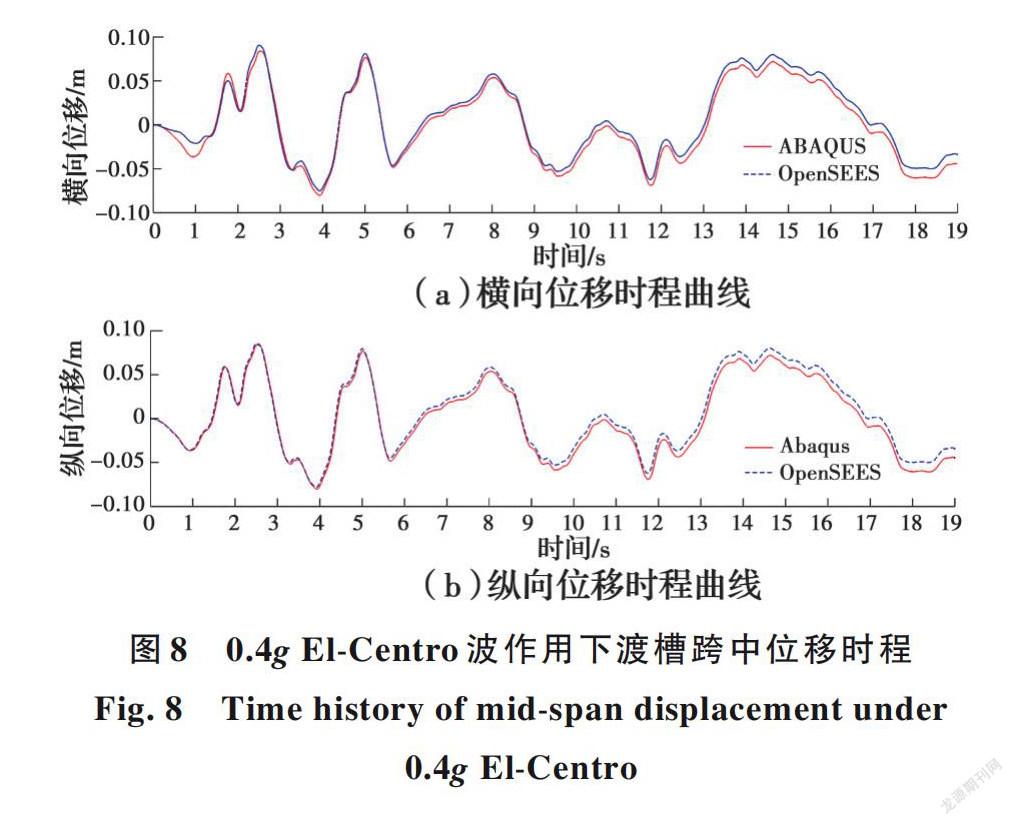
为验证基于OpenSEES分析平台的渡槽有限元模型的准确性，基于ABAQUS有限元平台建立了相同工况下的有限元模型，并从渡槽结构圆频率、线性时程分析和非线性时程分析3个方面开展比较研究，如图6～图8所示。

根据比较研究可知，基于OpenSEES平台的渡槽结构有限元模型准确可靠，可用于开展渡槽结构的动力响应分析和可靠性研究。

1.2 混凝土随机损伤本构关系模型

混凝土随机损伤本构关系模型可较为完整地诠释混凝土材料的非线性和随机性[8]，因此本文，选用该模型模拟渡槽结构混凝土力学参数的随机性。将混凝土任一代表性体积元抽象为并联微弹簧系统，且单根微弹簧服从理想弹脆性应力—应变关系[8]。通过研究细观微弹簧的随机断裂，可进一步得出混凝土材料的随机损伤演化规律。

该模型可将损伤表征为[6，15]

式中：D为混凝土损伤因子；A f为断裂面积；A 0为总面积；N为弹簧总数；n为在当前状态下的断裂弹簧根数；Δ i为第i根弹簧的断裂应变量；H（⋅）为Heaviside函数；ε为应变。

令弹簧总数趋于无穷大，损伤变量可按式（2）表达。

式中：Δ（x）为一维断裂应变随机场；x为坐标。

依据连续介质损伤力学理论[8，11]，混凝土一维损伤本构模型可表述为

式中：σ为混凝土应力；E 0为混凝土初始弹性模量；ε p为混凝土塑性应变。

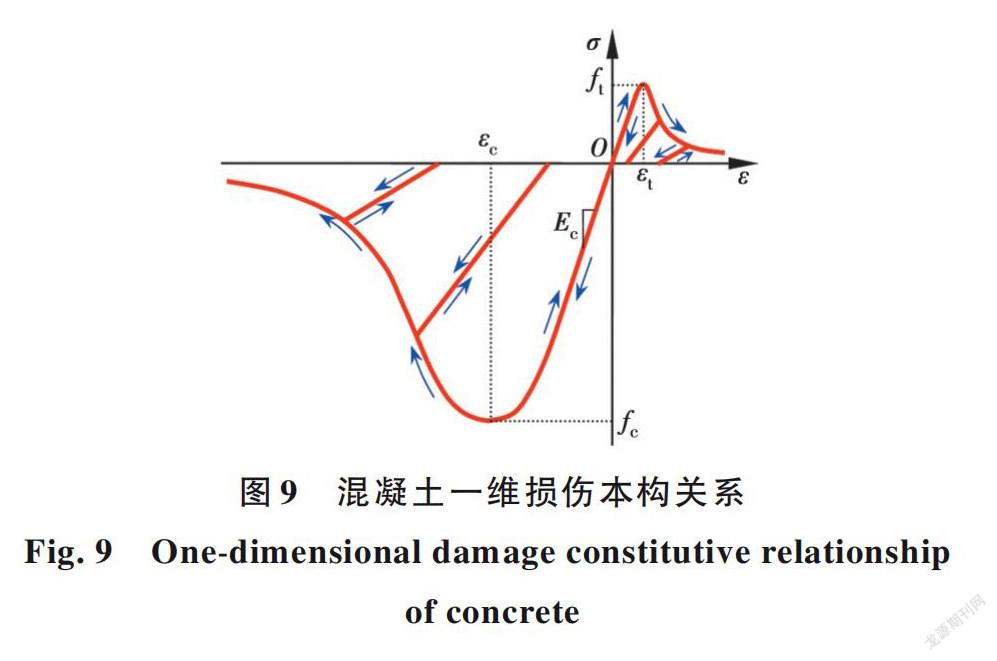
基于混凝土一维损伤本构模型，混凝土在一维反复加、卸载作用下的应力一应变特性可用图9所示曲线表征。

根据混凝土随机损伤本构关系模型，依据后续生成的混凝土材料力学参数样本，基于规范的混凝土应力一应变曲线，识别混凝土随机损伤本构模型中的基本参数，然后把基本参数代入到渡槽结构有限元模型中基于混凝土隨机损伤本构关系模型开发的ConcreteD材料本构，即可为开展渡槽结构的地震响应分析做好铺垫。

2 复合随机下的渡槽结构抗震可靠性分析方法

2.1 工程随机地震动的物理模型

开展渡槽结构在复合随机作用下的动力响应分析，需要构建随机地震动模型，以获取包含完整概率信息的随机地震动样本。为了真实反映地震动对结构的影响，Wang等[16]、Ding等[17-18]进行了一系列研究工作，提出工程随机地震动的物理模型，该模型引入了“震源一传播途径一局部场地”的物理机制，地震动加速度时程可表达为

式中：A R（Θ α，ω）为Fourier幅值谱；Φ R（Θ α，ω）为Fourier相位谱；Θ α为随机源参数。

随机地震动模型是开展随机地震响应分析的理论基础。把已知随机地震动参数样本代入到上述地震动加速度时程表达式，可求出地震动加速度时程数据样本，可为后续渡槽结构随机动力响应分析和可靠性求解做好铺垫。

2.2 基于概率密度演化的渡槽结构复合随机动力分析

在面对渡槽等复杂结构体系时，传统的复合随机分析方法尚无法给出解决方案。概率密度演化方法从理论和实践上解决了可靠性分析中随机耦合问题带来的困难，突破了传统复合随机分析方法研究复杂结构体系的瓶颈[11]。因此，本文采用概率密度演化方法开展渡槽结构的复合随机分析。

依据概率密度演化方法，考虑结构力学性能和外部激励的随机性[18]，可将渡槽结构的运动方程广义表述为

式中：M和C分别为渡槽结构的质量矩阵和阻尼矩阵；Ü（t）、U̇（t）和U（t）分别为渡槽结构响应的加速度、速度和位移矢量；f（U，t）和F（t）分别为渡槽结构的恢复力和外部荷载矢量；Ψ=（Ψ 1，Ψ 2…Ψ n）为渡槽结构包含的所有随机参数矢量；n为基本随机变量的个数；t为时间[6]。

设X=（X 1，X 2…X m）T为渡槽结构地震响应分析中感兴趣的响应量，则依据概率守恒原理，渡槽结构随机动力响应的概率密度满足偏微分方程[6，19-20]

当研究渡槽机理结构某一个地震响应量时，式（6）可退化为一维偏微分为程

式中：Ẋ（ψ，t）为响应量的广义速度。

式（6）的初始条件为

式中：x 0为x的初始值；δ（⋅）为Dirac delta函数。

式（6）为广义概率密度演化方程，它可揭示渡槽结构在地震作用下响应的概率信息随时间演化规律。联合求解式（5）、式（7）和式（8），可获得渡槽结构响应量的概率密度函数[6]

进而得到给定阈值下X lim的渡槽结构时变可靠度

在此基础上，将从渡槽结构抗震可靠性的角度考察渡槽结构在随机参数与随机激励耦合作用下的随机动力响应，并以此探究渡槽结构抗震可靠性评估方法。

3 复合随机下的渡槽结构抗震可靠性分析

为了更好地研究渡槽结构的抗震性能，把渡槽结构抗震可靠度设置为一个性能目标，并把渡槽结构墩顶横向位移角响应[5]作为衡量渡槽结构抗震可靠度的重要指标。

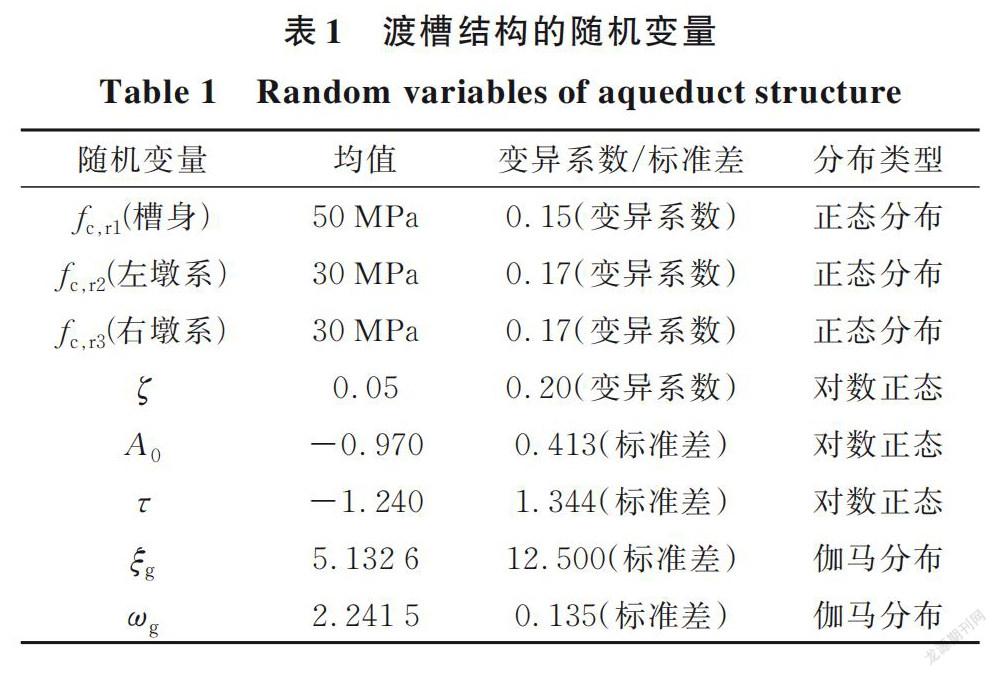
由表1可知，复合随机分析中包含的随机源参数包括f c，r1（槽身）、f c，r2（左墩系）、f c，r3（右墩系）、ζ、A 0、τ、ξ g、ω g共计8个随机源参数，其中，前4个参数为混凝土随机参数，后4个参数为地震动随机参数。需要注意随机源的来源不同：即混凝土随机参数是由于材料性质及其内蕴的材料力学特性而导致的；地震动随机参数是由于其复杂的地球物理大环境而产生的。

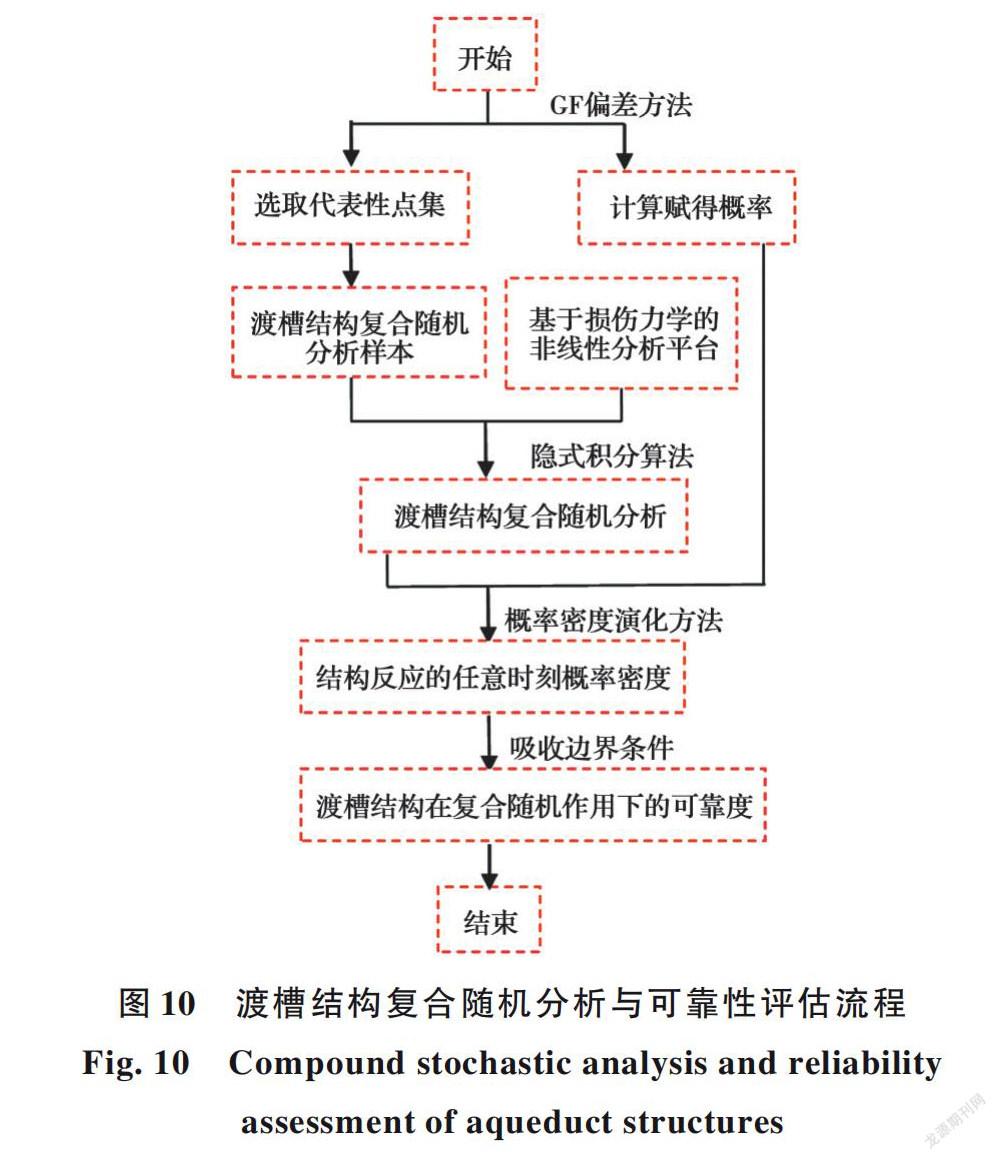
在复合随机分析时选择100个随机样本，参考上述理论，以表1中给出的随机源参数为依据，采用GF偏差选点方法[21]生成100个渡槽结构的复合随机样本，同时，计算每个样本所对应的赋得概率。这100组随机样本中每组随机参数与随机源参数值均比较接近，同时彼此又不相同，体现了材料力学性能参数和地震动激励参数的随机性。在此基础上，把100组随机地震动参数分别代入地震动加速度表达式即可得出相应的100组地震动加速度时程数据样本；与此同时，利用相应的100组材料力学性能参数，基于规范的混凝土应力一应变曲线，识别混凝土随机损伤本构模型中的基本参数，然后把基本参数代入到渡槽结构有限元模型中基于混凝土随机损伤本构关系模型开发的ConcreteD材料本构，即可得出100个渡槽有限元模型分析样本。把与之对应的100组地震动加速度时程数据样本分别加载到100个渡槽有限元分析模型样本中，即可开展渡槽结构的复合随机地震响应分析，并以此得出相应的分析结果。利用编写的后处理程序可提取渡槽结构墩顶横向位移角（R μ）[5]等地震响应相关数据，同时，把上述数据代入到概率密度演化方程，依据赋得概率可获取渡槽结构墩顶横向位移角响应量的概率密度演化信息。通过与吸收边界条件相结合，可开展渡槽结构在复合随机作用下的动力响应分析和抗震可靠性研究，求解流程如图10所示。

依据上述求解流程，以基于混凝土随机损伤本构关系的渡槽有限元模型为基础，同时考虑了渡槽结构力学参数的随机性和地震激励的随机性，并与“仅考虑地震激励随机性工况”对比分析，挖掘渡槽结构在复合随机作用下的响应规律和抗震可靠性。

由于每个维度随机变量的单位与量级不一致，需要对其变换到标准空间后再进行选点，并分别对100个代表性复合随机样本点进行动力响应分析，求解渡槽结构墩顶位移角等信息的均值、标准差及相关概率密度信息。

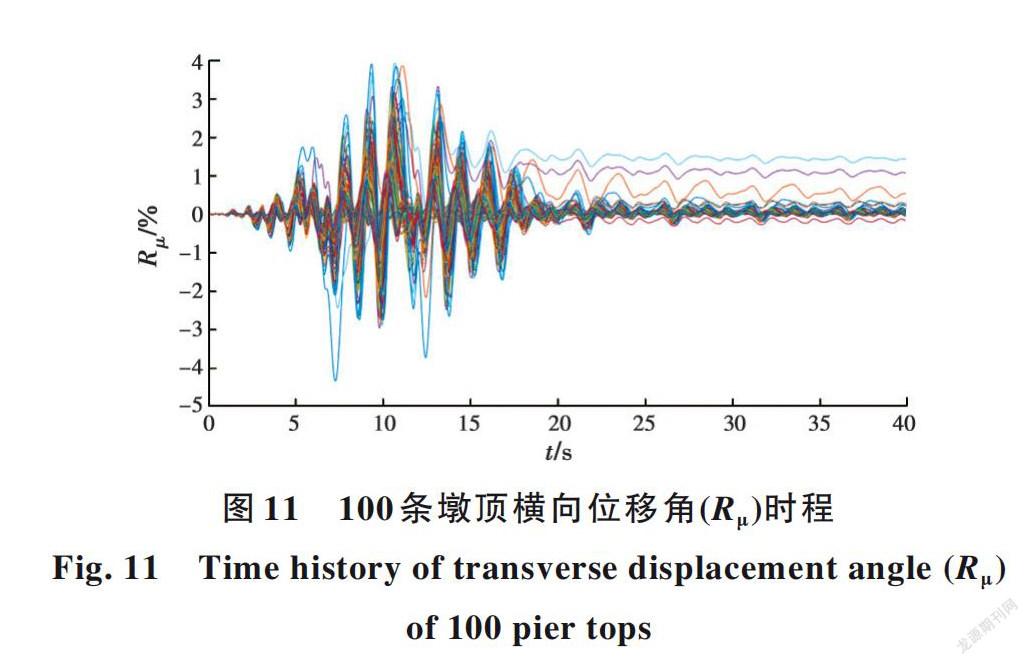
由图11所示的位移时程曲线可知，不少渡槽样本的槽墩约在18 s后出现较大的不可恢复变形，这是因为在复合随机和非线性的多重作用下，渡槽结构会较快地进入强非线性阶段，产生不可恢复残余变形的结果。

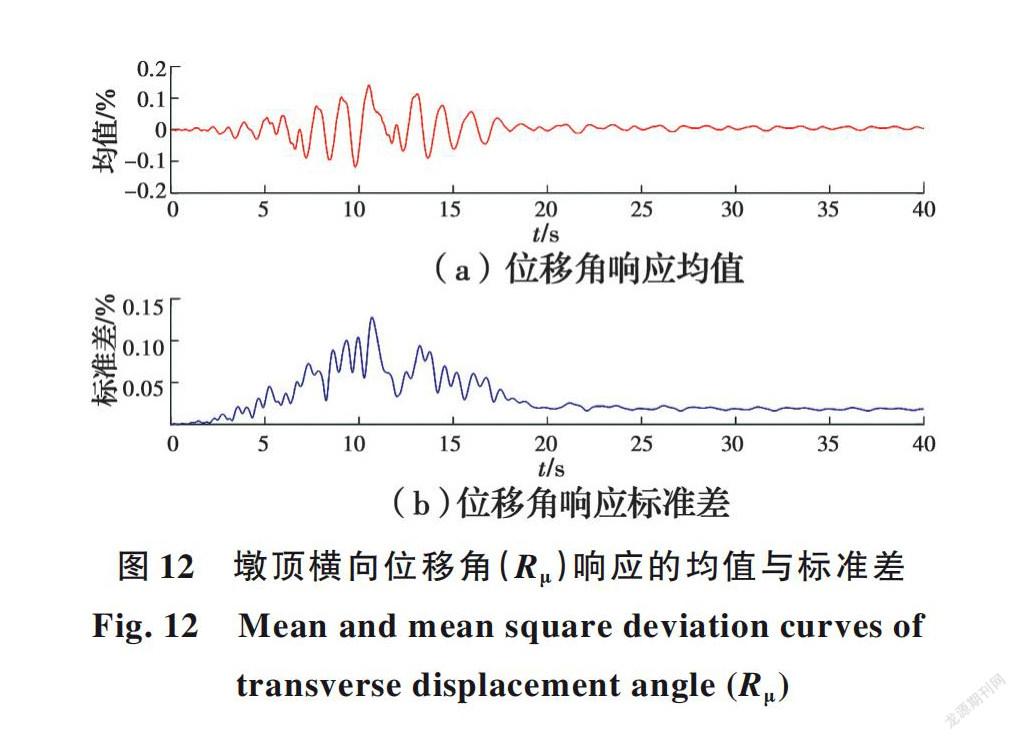
图12（a）为渡槽结构在复合随机作用下的墩顶横向位移角响应的均值，图12（b）为渡槽结构在复合随机作用下的墩顶横向位移角响应的标准差。通过分析图12（b）可发现，渡槽结构在复合随机作用下的墩顶位移角响应约在5～17 s期间表现出巨大的变异性，说明复合随机作用对渡槽结构在动力响应下的位移和非线性变形的随机性影响较大。

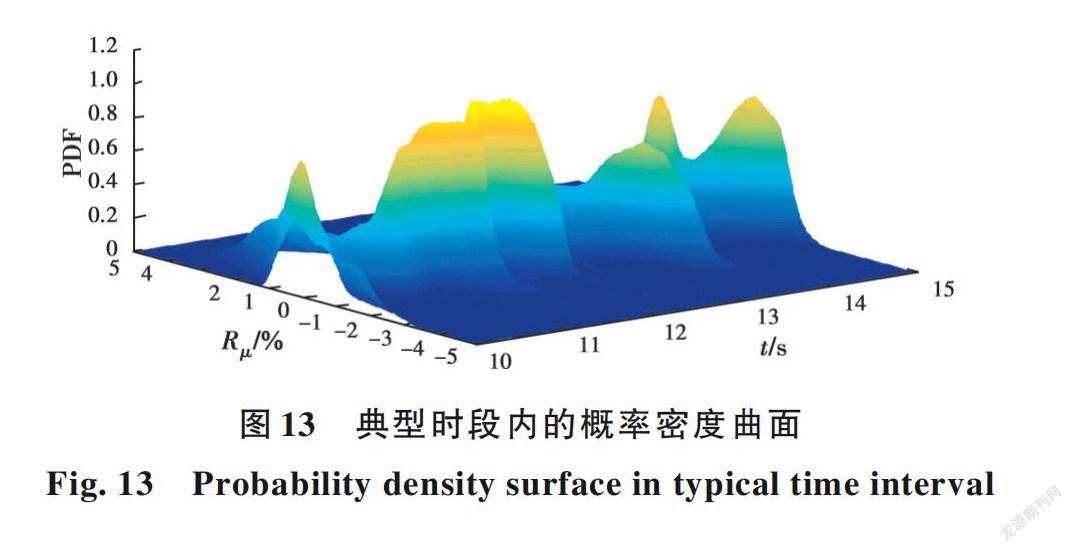
據图11、图12可知：在10～15 s的时间区间内，渡槽结构在地震激励下的位移响应值、均值和标准差相对比较大，因此，选取该区间内的概率密度演化曲面比较有代表性。

图13给出了渡槽横向位移角响应在10～15 s期间概率密度随时间演化的曲面图。由图13可知，该曲面形似延绵起伏的山峰，包含了用于描述渡槽结构性能随时间变化的概率信息，是开展渡槽结构地震响应和抗震可靠性研究的基础。

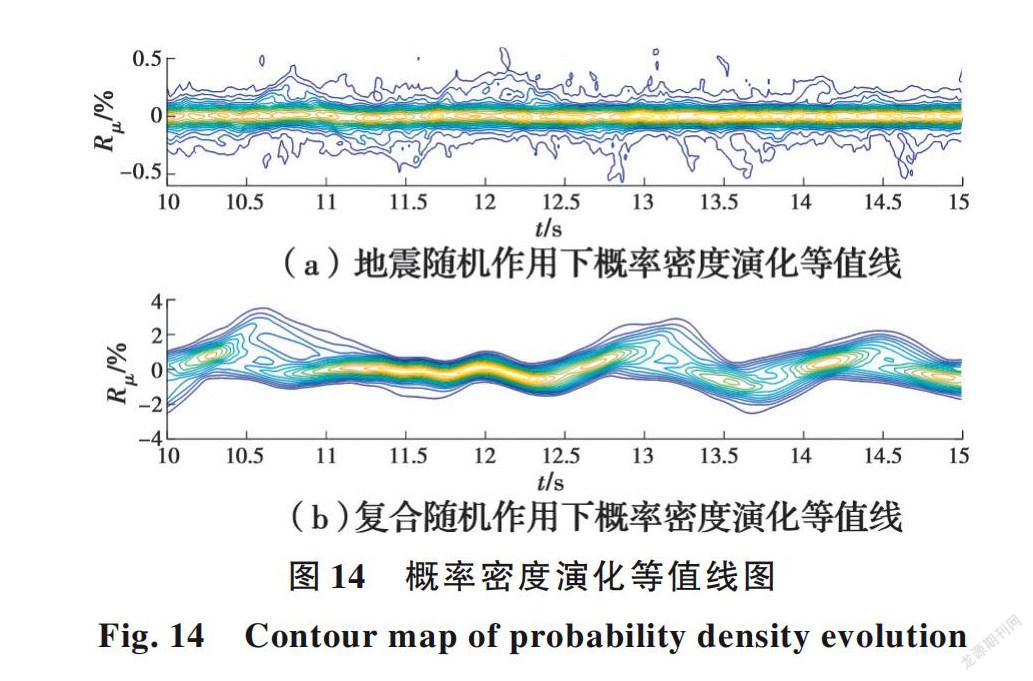
图14为概率密度演化信息等值线图，其中，图14（a）为仅考虑地震随机作用下的等值线图，图14（b）为考虑地震激励随机性和混凝土力学参数随机性耦合作用下的等值线图。对比研究发现，图14（a）由于仅考虑地震随机作用，表现出来的非线性相对较弱，其等值线变化幅度较小。在复合随机作用下，如图14（b）所示表现出强非线性下的等值线波动性更大，波动范围更大。深入分析可知：在相同时间段内，结构相当一部分进入非线性阶段，内外两种随机因素的共同作用与结构材料非线性交织在一起，使复合随机工况下渡槽结构地震随机演化效应明显得到加强。

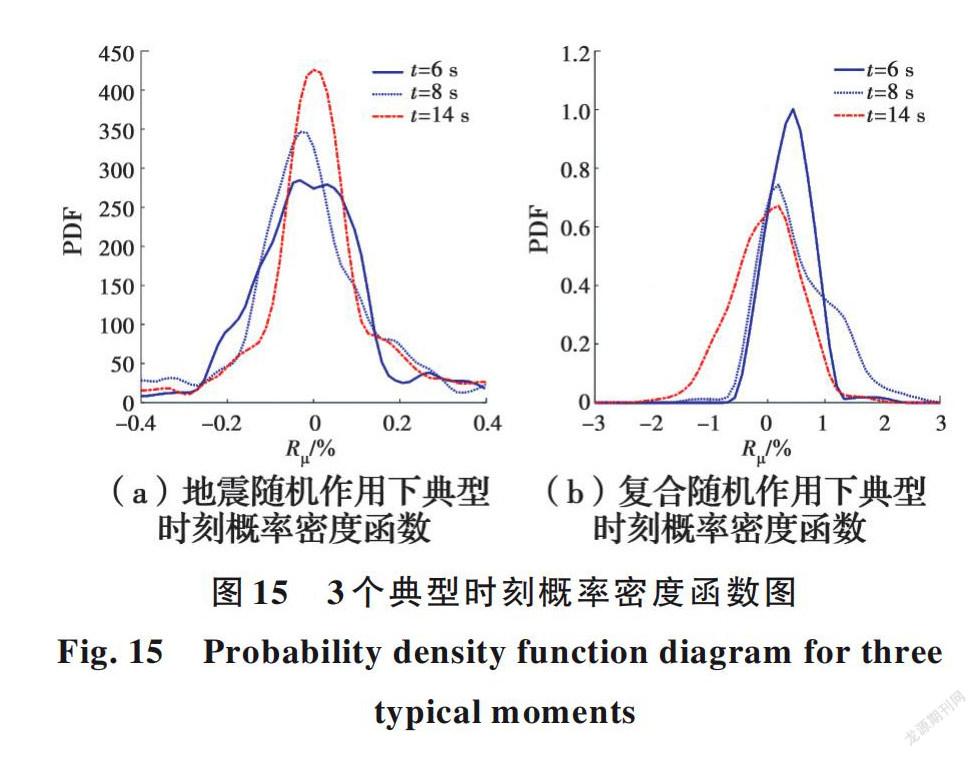
图15为3个典型时刻的概率密度函数，其中，图15（a）为仅考虑地震随机作用下的3个典型时刻的概率密度函数图，图15（b）为考虑地震随机性和混凝土力学参数随机性耦合作用下的3个典型时刻的概率密度函数图。对比图15（a）、（b）可知，在3个相同的时间节点下，复合随机工况下的概率密度函数更加离散，表现在3个时间段的离散区间扩展了7倍以上。造成这一结果的原因在于：复合随机作用下，非线性与随机性耦合作用更为明显，结构响应的随机性也变得更强，相应地也导致其概率密度信息更为丰富，进一步说明复合随机作用下渡槽结构地震响应的程度变得更加复杂与多变。深入研究图15（b）发现，尽管6 s和8 s两曲线时间间隔比较近，但两者的概率密度函数仍表现出巨大的差异性，再次说明渡槽结构在复合随机作用下地震响应的巨大变异性。

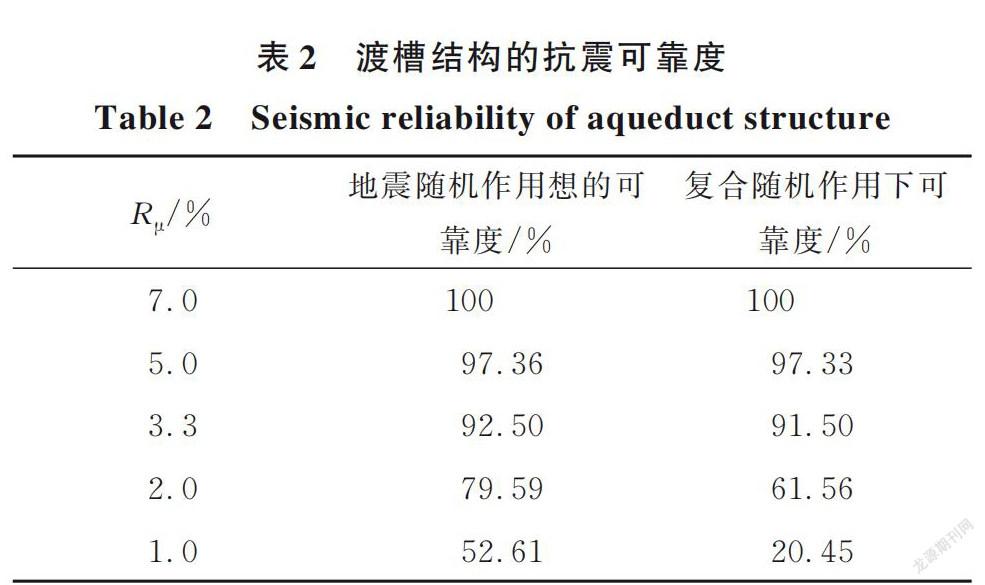
根据上述分析，为了获得渡槽结构的抗震可靠度指标，可施加与失效阈值相应的吸收边界条件来实现。在0.8g地震动横向激励作用下，对渡槽左墩位移角阈值R μ分别取7.0%、5.0%、3.30%、2.0%和1.0%，可求得其相應的可靠度，如表2所示。

分析表2发现，在阈值相对较大时，两工况相应的可靠度非常接近，且工况2下的渡槽结构可靠度稍微偏低。随着阈值的不断减小，工况2所求得的可靠性明显偏低，且两者之间的差距呈现增大趋势。

同时考虑混凝土力学参数随机性和地震激励随机性的影响，必然会造成以上两种随机因素发生叠加作用、放大渡槽结构复合随机样本的地震响应，造成在复合随机作用下渡槽结构的位移响应较大，并且使位移响应具有较大的离散型。根据抗震可靠性原理可知，在阈值一定的情况下，墩顶位移角响应越大，发生超越概率的可能性也越大。这也会造成渡槽结构在复合随机作用下的抗震可靠性偏低。换言之，以上分析结果与可靠性经典理论一致。

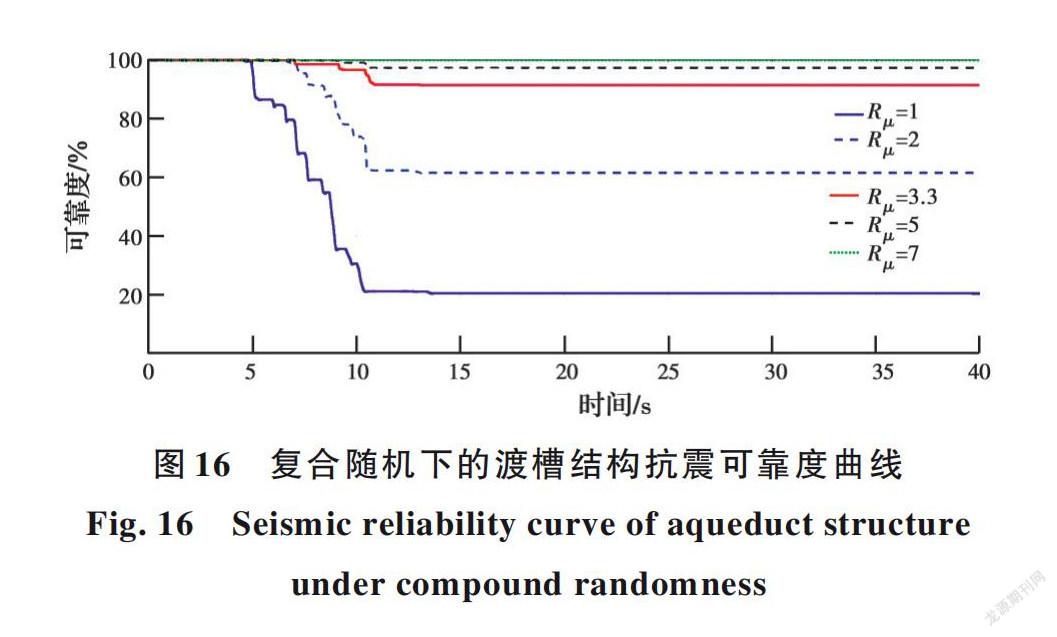
为了更直观地反映渡槽结构在不同阈值下的变化趋势，特绘制渡槽结构在复合随机作用下的可靠度曲线，如图16所示。由图16可知，在5个不同的失效阈值下，渡槽结构抗震可靠度在20.45%～100%之间有较大幅度的变化。

4 结论

基于混凝土随机损伤力学模型和概率密度演化理论，开展了渡槽结构抗震可靠性研究，得到如下结论：

1）从渡槽结构可靠度这一性能目标出发，提出渡槽结构在复合随机作用下的非线性动力响应和可靠性分析方法。

2）与单一地震随机作用比较发现，复合随机作用下渡槽结构的位移响应明显加剧，且位移响应产生的残余变形和位移的变异性均较大。

3）复合随机作用下，渡槽结构的抗震可靠度低于仅考虑地震随机作用下的渡槽结构抗震可靠度。

随着阈值的减小，渡槽结构在复合随机作用下的可靠度与单一随机地震作用下的可靠度之间的差距呈不断增大趋势，且渡槽结构在两种工况下的可靠度均不断减小。因此，复合随机作用对渡槽结构抗震可靠度的影响不容忽视。

参考文献

[1]安旭文，朱暾.罕遇地震下渡槽槽架结构弹塑性侧移的可靠度分析[J].武汉大学学报（工学版），2010，43（5）：604-607.AN XW，ZHU T.Reliability analysis of elastoplastic displacements of aqueduct structure under infrequent earthquake[J].EngineeringJournalofWuhan University，2010，43（5）：604-607.（in Chinese）

[2]刘章军，方兴.大型渡槽结构随机地震反应与抗震可靠度分析[J].长江科学院院报，2012，29（9）：77-81.LIU ZJ，FANG X.Stochastic earthquake response and seismic reliability analysis of large-scale aqueduct structures[J].Journal of Yangtze River Scientific Research Institute，2012，29（9）：77-81.（in Chinese）

[3]MA WY，CHENG YY，LIU P，et al.Research on system reliability of the minghe aqueduct in the middle routeprojectofthesouth-to-north[J].Applied Mechanics and Materials，2012，229/230/231：2601-2605.

[4]张多新，崔越越，王静，等.大型渡槽结构动力学研究进展（2010—2019）[J].自然灾害学报，2020，29（4）：20-33.ZHANG DX，CUI YY，WANG J，et al.Research progress in structural dynamics of large scale aqueduct（2010-2019）[J].Journal of Natural Disasters，2020，29（4）：20-33.（in Chinese）

[5]张威，王博，徐建国，等.随机地震作用下大型渡槽结构可靠性求解方法[J].水力发电学报，2018，37（10）：113-120.ZHANG W，WANG B，XU JG，et al.Solution to reliability of large aqueduct structures subjected to random earthquake ground motions[J].Journal of Hydroelectric Engineering，2018，37（10）：113-120.（in Chinese）

[6]张威，王博，徐建国，等.地震作用下大型渡槽结构输水功能可靠性分析[J].土木与环境工程学报（中英文），2020，42（4）：144-152.ZHANG W，WANG B，XU JG，et al.Water-conveyance functional reliability analysis of large-scale aqueduct structures subjected to earthquake excitations[J].Journal of Civil and Environmental Engineering，2020，42（4）：144-152.（in Chinese）

[7]ZHOU H，LI J.Energy-based collapse assessment of concretestructuressubjectedtorandomdamage evolutions[J].Probabilistic Engineering Mechanics，2020，60：103019.

[8]李杰，吳建营，陈建兵.混凝土随机损伤力学[M].北京：科学出版社，2014.LI J，WU JY，CHEN JB.Stochastic damage mechanics of concrete structures[M].Beijing：Science Press，2014.（in Chinese）

[9]李杰.工程结构整体可靠性分析研究进展[J].土木工程学报，2018，51（8）：1-10.LI J.Advances in global reliability analysis of engineering structures[J].China Civil Engineering Journal，2018，51（8）：1-10.（in Chinese）

[10]ZHOU H，LI J.Physical synthesis method for global reliabilityanalysisofengineeringstructures[J].Mechanical Systems and Signal Processing，2020，140：106652.

[11]周浩，李杰.基于不同本构模型的混凝土结构地震倒塌对比分析[J].建筑结构学报，2016，37（9）：8-18.ZHOU H，LI J.Comparison study on seismic collapse of concrete structures with different constitutive models[J].Journal of Building Structures，2016，37（9）：8-18.（in Chinese）

[12]LI J，ZHOU H，DING YQ.Stochastic seismic collapse and reliability assessment of high-rise reinforced concrete structures[J].The Structural Design of Tall and Special Buildings，2018，27（2）：e1417.

[13]MAHASUVERACHAI M.Inelastic analysis of piping andtubularstructures[R].Berkeley：Earthquake Engineering Research Center，University of California，1982.

[14]KABA S，MAHIN SA.Refined modeling of reinforced concrete columns for seismic analysis：Earthquake engineering research center[R].Berkeley：Earthquake Engineering Research Center，University of California，1984.

[15]李杰，冯德成，任晓丹，等.混凝土随机损伤本构关系工程参数标定与应用[J].同济大学学报（自然科学版），2017，45（8）：1099-1107.LI J，FENG DC，REN XD，et al.Calibration and application of concrete stochastic damage model[J].Journal of Tongji University（Natural Science），2017，45（8）：1099-1107.（in Chinese）

[16]WANG D，LI J.Physical random function model of ground motions for engineering purposes[J].Science China Technological Sciences，2011，54（1）：175-182.

[17]DING YQ，PENG YB，LI J.A stochastic semi-physical model of seismic ground motions in time domain[J].Journal of Earthquake and Tsunami，2018，12（3）：1850006.

[18]DING YQ，PENG YB，LI J.Cluster analysis of earthquake ground-motion records and characteristic period of seismic response spectrum[J].Journal of Earthquake Engineering，2020，24（6）：1012-1033.

[19]LI J，CHEN JB.Stochastic dynamics of structures[M].Singapore：John Wiley&Sons，2009.

[20]CHEN JB，LI J.Dynamic response and reliability analysisofnon-linearstochasticstructures[J].Probabilistic Engineering Mechanics，2005，20（1）：33-44.

[21]CHEN JB，YANG JY，LI J.A GF-discrepancy for point selection in stochastic seismic response analysis of structures with uncertain parameters[J].Structural Safety，2016，59：20-31.

（编辑

胡玲）