基于CPFD方法的机制砂气流分级模拟与试验研究
陈 理
(中铁建重庆投资集团有限公司,重庆 401121)
1 引言
天然砂作为短期内不可再生的建筑骨料材料,经过几十年的高强度开采,资源已接近枯竭。同时国家出于安全与环境保护考虑已出台了一系列关于天然砂的限采禁采政策,导致本就产量不足的天然砂更加紧缺。因此,大力推广使用机制砂作为其替代品十分必要。根据筛分方式的不同,机制砂制砂方式可分为湿法和干法制砂。相比于湿法,干法工艺受水源、气候和温度影响小,更节约水资源,所需生产场地较小且易于集中控制,分离出的石粉也可被二次回收用于改善砂石粒度。在倡导环境保护、机制砂级配质量要求越来越高的今天,干法制砂的气流分级方式越来越受到业内人士的青睐。其中重力风选设备是机制砂工艺的核心设备之一,其气流分级效果将直接影响骨料的质量与产量。
在机制砂行业,关于重力风选设备的研发和使用已初具规模,但对于砂石的分选仍停留在粗分阶段,得到的成品机制砂级配水平不高,分级效果有待提升。国内外学者基于Fluent等数值模拟软件,在气固两相流仿真领域已有一定的进展。通过对数值模型的初始条件、参数进行假设和调整,结合一系列物理对照实验,验证了数值模拟对于预测物料气流分级过程的可行性与准确性;并基于此对风选设备内部气流场、颗粒场和气流分级效果的影响因素进行了研究。但这些研究都主要集中在谷物风选、垃圾风选等领域,机制砂与其他物料相比粒径分布广且连续,现有对于机制砂气流分级的研究还存在很大空缺。
因此,本研究针对机制砂风选过程,借助基于CPFD方法的Barracuda VR软件,对其进行了数值模拟,分析了不同气流速度下,风选设备对于机制砂的气流分级效果与内部砂石的气流分级运动规律,并对模拟结果进行了验证。
2 机制砂气流分级设备几何模型
本文用于模拟的风选设备整体长度为2.25 m,高度为1.58 m,厚度为0.6 m,共有1个砂进料口,1个风入口,1个风出口,8个砂出口,其中风出口主要用于排出粒径较小的砂颗粒。该模型在厚度方向上保持一致,砂进料口宽300 mm,风入口宽300 mm,风出口宽度600 mm,砂出口1~8宽分别为200 mm,200 mm,200 mm,200 mm,200 mm,350 mm,250 mm和400 mm。机制砂经砂入口进入,不同粒径的砂颗粒在风选室内经风入口气流和重力共同作用下横向位移不同,最终落入不同的砂出口。
3 机制砂气流分级过程的数值模型
3.1 模拟方法
目前研究气固两相运动过程的主要方法有欧拉-欧拉法和欧拉-拉格朗日法。而在机制砂气流分级过程中,同一时间在设备内的砂颗粒数量极多,且其运动状态明显区别于流体,颗粒运动也会反作用于空气流,改变气相的流动状态。相比于欧拉-欧拉法,欧拉-拉格朗日法更能对该系统进行更好的描述。近年来发展了一种新型的多相流质点网络模型(MultiphaseParticle In Cell, MP-PIC),该方法基于欧拉-拉格朗日法,旨在计算拥有大量固体颗粒的两相流耦合问题。本文使用的软件Barracuda是一种比较成熟的、专门针对工业领域的大尺度气固流动模拟的商业软件,其模拟方法便是基于MP-PIC模型的计算颗粒流体力学(Computational Particle Fluid Dynamics, CPFD)方法。通过该方法能较为快速准确地求解含有大量固体颗粒的气固两相流动问题,对其进行全尺寸分布的模拟,求得颗粒流动的拉格朗日意义下的各种物理信息。因此本文考虑使用基于CPFD方法的Barracuda软件来研究机制砂的风选过程。
3.2 控制方程
在CPFD模拟计算过程中,气相采用欧拉方法处理,固相则使用拉格朗日方法处理并与气相方程相耦合。
对于气固两相流:

气相质量守恒方程为:

气相动量守恒方程为:
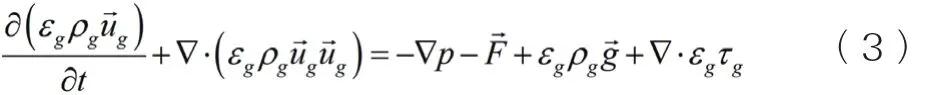
颗粒相动量方程为:

4 机制砂气流分级数值模拟
4.1 模型建立
将风选设备的几何模型导入Barracuda中,进行正交网格划分,进行建模模拟,共计划分127 728个网格单元。
4.2 模拟方案
本文所用于气流分级研究的机制砂取自于贵州某项目。根据《建筑用砂GBT14684-2011》中粒径划分标准,本文将机制砂划分为0~0.15 mm,0.15~0.3 mm,0.3~0.6 mm,0.6~1.18 mm,1.18~2.36 mm,2.36~4.75 mm六种粒径范围。经现场筛分实验测得其粒度分布如表1。
设进料机制砂采用表1粒度分布,进料量为4.17 kg/s,进料速度为0 m/s,分别模拟风入口气流速度为12,14,16,18,20 m/s时的机制砂气流分级过程,用以研究不同风速下机制砂风选运动规律与风选设备对于不同粒径机制砂的分级效果。

表1 机制砂粒度分布
4.3 模拟参数与边界条件设置
在模拟参数设置中,假设流体为等温不可压缩流,温度固定为300 K。假设机制砂颗粒为球形,且在进料时均匀分布在进料口平面。由于只包含机制砂的物理分级过程,故在模拟时不考虑化学反应。
设置空气为气相,机制砂为固相。风入口、风出口、砂入口和砂出口与大气相连。其中风入口设为速度入口边界,只允许气相通过。砂入口、砂出口与风出口设为压力出口边界,初始压力为常压,允许气固两相通过。
CFL数是计算流体力学中的收敛条件判断数,CFL值越接近1,计算结果越准确。在模拟运算过程中,需要通过调整时间步长以控制CFL数,减少误差。在Barracuda中,对于过大的时间步长,计算时会自动调整,使其控制在0.8~1.5间。在文章的模拟研究中,时间步长设置为0.002 s,模拟10 s的机制砂风选过程。设置设备的边界压强条件为标准大气压(101 325 Pa),xyz方向重力设置为0,-9.8 m/s,0。
4.4 模拟结果与分析
随着风入口风速增大,设备内的气流场流型也随之变化。气流从风入口进入风选室后,在风入口周围沿水平方向气流速度迅速降低,并形成一条主要气流带,最终流出风选室。当v=12 m/s和14 m/s时,风速较小,主要气流呈抛物轨迹,沿斜下方向从砂出口6~8流出;当v=16 m/s,18 m/s和20 m/s时,主要气流的轨迹更趋于水平。
随着风速增大,0~0.6 mm的细颗粒受风速影响较大。其中粒径0~0.15 mm和0.15~0.3 mm砂石由主要集中于砂出口8逐渐移动至砂出口9,即风出口处;粒径0.3~0.6 mm砂石的落点由砂出口6,7和8逐渐移至砂出口8,且当v=18 m/s时,绝大部分砂石落至砂出口8。而粒径0.6~1.18 mm砂石分布较为分散,随风速增大,落点由砂出口3~5右移至5~8。粒径1.18~2.36 mm与2.36~4.75 mm粗砂受风速的影响较小,1.18~2.36 mm砂石从砂出口2~3吹至3~5,而2.36~4.75 mm砂石仍主要集中在砂出口2~3。
综上所述,该单风入口结构的风选设备虽能对各粒径砂石进行简单的气流分级,但各砂出口收集的砂分级精度不高,仍存在两种或以上粒径砂互相混合,同时单纯改变气流速度对不同粒径砂的分级影响不均,导致对设备整体分级效果的影响有限。
5 机制砂气流分级试验
5.1 试验过程
建立与几何模型对应的物理模型,用以验证模拟的准确性。在砂出口下方放置有砂石收集箱,用以收集砂出口排出的砂颗粒。将各出口收集的砂使用标准砂筛对其进行筛分,记录与计算不同粒径砂石的质量及其占比。
用于试验的机制砂粒度分布和进料量与模拟相同。进行试验时,待风机风速稳定后,由装置上部的传送带匀速供料,并使用秒表记录喂料时间。分别测量风速为16 m/s,18 m/s和20 m/s时的机制砂气流分级试验结果,每组风速测试3次,每次试验进行10 s,取其平均值。
5.2 试验结果与分析
图2为各砂出口累计质量占砂石总入料量比值与试验对比。由图可知,各砂出口累计质量的试验结果与模拟结果基本吻合,累计质量占比存在一定误差。出现误差可能有以下原因:模拟所设置的边界条件与试验边界条件存在一定误差;试验过程中风入口的气流并不是完全均匀且稳定,可能受风机和管道影响;砂筛分时可能存在一定人工误差。后续可对风选设备和风机管道改进优化,减少干扰气流来源,提升试验精度。

图1 16 m/s风速下各砂出口累计质量占比的模拟-试验对比
6 结论
文章通过CPFD数值模拟方法,模拟了风选设备在不同风速下的机制砂风选过程,对比分析了风速变化对气流场,砂石运动和分离率的影响规律,分析了该风选设备对于机制砂的气流分级能力,得到了以下主要结论:
(1)随风入口气流速度增大,设备内的气流场流型也随之变化,气流轨迹由抛物趋于水平,同时在风出口下方近壁处会产生小型涡流。整体分布为中部大,靠近上下边界处小,在风入口处有最大风速,气流高速区域主要集中于风入口附近和气流高速带,其他区域流速普遍较小。
(2)风选过程中,砂石主要集中分布在砂出口2、3、4和8处,设备中部的砂石数量较少,且各粒径砂石的横向位移不同。其中,粒径0~1.18 mm砂石分层分布较为明显,而粒径1.18~4.75 mm粗砂的分离效果较差。当v=16 m/s时,粒径0~0.15 mm和0.15~0.6 mm砂石分布较为集中,分别分布于风出口与砂出口8;而粒径0.6~1.18 mm砂石分布较为分散;粒径1.18~2.36 mm和2.36~4.75 mm的砂石主要集中于砂出口2~4。
(3)随风速增大,整体砂石向右侧砂出口集中,砂出口1~3的砂石移至砂出口4~9,砂出口2和风出口的砂石累计质量变化较大。风速改变能显著影响0~0.6 mm细颗粒的风选运动,随风速增大,这几种砂石能在风选室右半部分中完全分层分离;而粒径1.18~4.75 mm粗砂受风速的影响较小,且随着风速增大,两种粒径砂石仍互相混合。
(4)通过物理试验与模拟结果进行对比,可知风选过程的模拟结果和试验吻合度较好,验证了使用该方法与软件进行模拟的可靠性。

