某型高速列车车厢连接处脉动压力的预测与控制*
张文敏 李启良 贾尚帅 韩铁礼 王毅刚
(1.中车唐山机车车辆有限公司技术研究中心, 063035, 唐山; 2.同济大学上海地面交通工具风洞中心, 201804, 上海∥第一作者, 工程师)
我国是世界上高速铁路发展速度最快、规模最大的国家。高速列车以超过300 km/h的速度运行时,列车的转向架、受电弓和车厢连接处会产生强烈的气动噪声,严重影响了车内乘客的乘坐舒适性,因而长期受到广泛关注。
车厢连接处是高速列车降噪隔振的薄弱部位,车外气流产生的气动噪声较易通过车厢连接处进入车内。目前,针对车厢连接处噪声的研究,大多基于压缩比例和简化的车厢连接处,采用试验与仿真方法,围绕噪声产生机理及其控制开展。文献[1]通过测量以300 km/h运行的高速列车车内噪声发现,车厢连接处的测点总声压级比车厢中央处的测点高14.6 dB,比车厢两端转向架上方车内测点约高2.0 dB。文献[2]给出法国TGV(高速铁路)系统的列车以350 km/h运行时,其车厢连接处外部测点噪声量值和峰值频率(76 Hz、196 Hz和276 Hz)的产生原因。文献[3]基于车厢端部二维空腔模型,研究了车厢端部上部倒角、上下同时倒角对于气动噪声的影响,发现设置车厢端部上端倒角可明显降低下游气动噪声。在平顺、光滑车厢连接上端圆角的基础上,再平顺、光滑下端的圆角,其降噪效果并不明显。文献[4]基于1∶8压缩比例设置了3节编组列车模型,研究了高速列车在350 km/h速度下全包风挡与半包风挡对车厢连接处气动噪声的影响。该研究发现,采用全包风挡时,列车运行方向声压级最大降幅为3.1 dB,横向声压级最大降幅为3.0 dB,垂向声压级最大降幅为2.4 dB。文献[5]采用非线性声学求解方法和FW-H方程获得车厢连接处近场和远场特性,发现车厢连接处呈现开式空腔噪声特征,存在42 Hz共振峰值,总声压级与车速的5次方成正比。在此基础上,提出并评估了半包风挡和全包风挡的控制方案。文献[6]提出了一种基于猫头鹰无声飞行仿生学的气动噪声分析与设计方法,确定湍流强度最小的关键形态参数,以用于车厢连接处噪声控制,从而达到较好的降噪效果。但是,针对车厢连接处的实车结构提出解决车厢连接处具体噪声问题的有效措施并不多,而基于射流的主动流动控制尚未涉及。
为此,本文以某型高速列车车厢连接处的噪声问题作为案例进行研究。该列车运行到350 km/h时,靠近第5节和第6节车厢连接处的乘务员室测点在中心频率为40 Hz时所对应的声压级高达105 dB,远大于其他频率的声压级,严重影响了乘务员的乘坐舒适性。本文通过试验和数值仿真手段找出车厢连接处噪声的产生原因,在此基础上评估基于波浪板的被动流动控制和射流的主动流动控制的效果,进而解决该噪声问题。
1 脉动压力预测
1.1 建立模型与体网格
目前线路上运行的高速列车通常为8节编组或16节编组,车长L超过200 m,车宽W约为3.5 m,车高H约为4.0 m。对如此大尺寸的高速列车进行实车脉动压力预测与控制,保守估计所建立的列车模型的体网格数将超过10亿个。为解决网格数过大、计算时间过长的问题,本文采用子域法,对实车车厢连接处的脉动压力进行计算。所谓子域法,是指仅选取整车计算的一部分,并在此基础上创建较小的计算域,如图1所示。已有对实车头型的研究表明[7],子域法得到测点和截面的平均流场和脉动流场特性与整车基本相同。本文所研究的车厢连接处也有类似的结论,受篇幅所限,不再赘述。

a) 8车编组高速列车模型
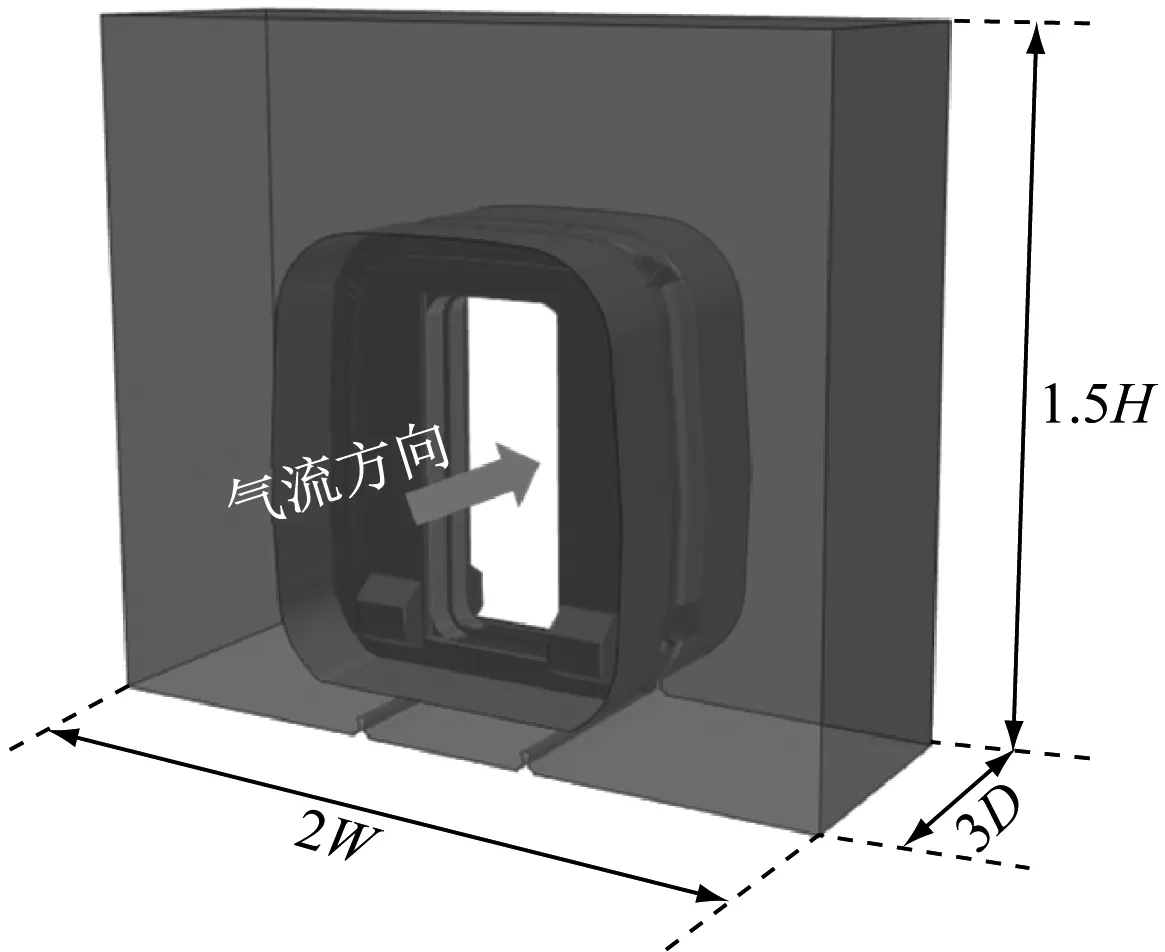
注:D为车厢端墙间距,约为0.7 m。 b) 第5节和第6节车厢连接处图1 基于子域法建立的车厢连接处模型Fig.1 Model of inter-coach based on subdomain method
如图1所示,模型的子域长、宽和高分别为3D、2W和1.5H。为了尽可能真实地模拟车厢连接处的气动特性,除部分小孔洞外,模型几乎保留了列车内、外风挡的所有细节。所有表面均划分为三角形网格,其中:外风挡网格的基本尺寸为8 mm,最小为2 mm;内风挡和端墙等部件的网格尺寸为8 mm;车身等较大表面的网格尺寸为16 mm;计算域的网格最大尺寸为32 mm。所有表面共生成了280万个面网格。
在此基础上,使用STARCCM+软件的Trimmer+layer策略生成计算域的体网格。对外风挡的四周进行网格加密,网格尺寸为8 mm。为了有效捕捉车厢连接处上、下缺口射流剪切层涡流的变化情况,对该区域进行网格细化,网格尺寸为4 mm。网格的加密位置如图2所示,其中:图2 a)标注为6-1等8处为外风挡所在加密区;图2 b)标注为3-1等4处为上、下缺口所在加密区。
为了更好地模拟壁面边界层流动,模型生成了第1层为0.025 mm的边界层网格,首层网格对应量纲为一的壁面距离约为2,满足延迟分离涡 (iDDES) 模型[8]对近壁网格的要求。模型中,除地面和轨道外的所有壁面均生成6层边界层网格,网格尺寸的增长率为1.2。整个计算域共生成约3 100万个体网格。
使用子域法进行脉动压力计算时,不应直接在进口处给定均匀来流的边界条件,而应将实车测试得到对应截面的速度、压力、湍动能和耗散率等作为边界条件。为此,在参考TB/T 3503.4—2018《铁路应用空气动力学 第4部分:列车空气动力学性能数值仿真规范》的基础上,本文建立了8节编组高速列车的实车气动仿真模型。该模型含头型、平直段、受电弓、转向架、轨道等结构部件。整个模型面网格总计约650万个。分别对所关注的车厢连接处进行网格加密,加密区域的网格尺寸为32 mm。除地面和轨道外,所有壁面均生成5层边界层网格,网格尺寸的增长率为1.2,首层网格对应量纲为一的壁面距离约为100,满足SSTk-w(剪切应力传输) 模型[9]对近壁网格的要求。整个计算域共计生成约1.2亿个体网格。

a) 外风挡加密区
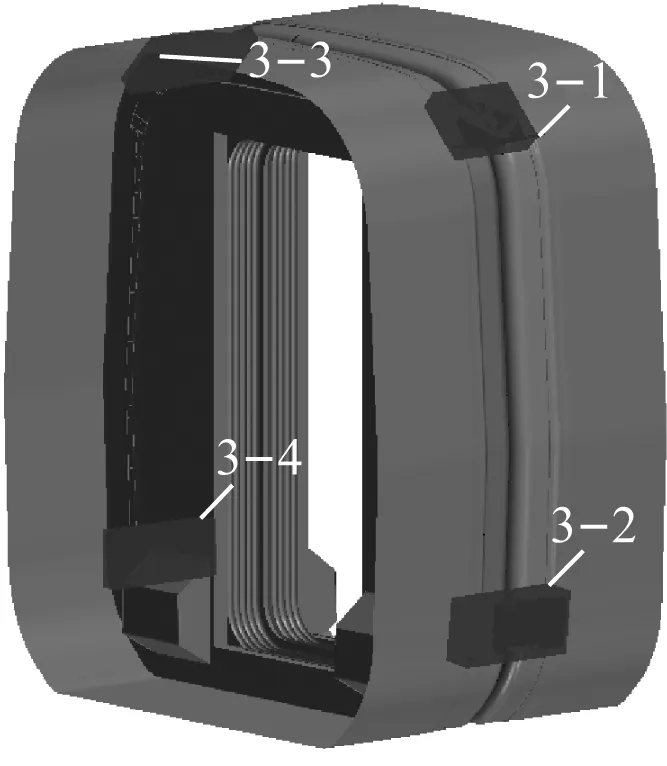
b) 上、下缺口加密区图2 对车厢连接处外风挡区域的体网格加密位置Fig.2 Densifying volume mesh of the outer windshield region of the inter-coach
设定子域的进口为速度入口,并指定速度为350 km/h。地面和轨道为移动壁面,其移动速度也为350 km/h。车轮为旋转壁面,设定角速度为214 rad/s,与之对应的轮边线速度也为350 km/h。经稳态迭代3 000步后,计算结果收敛。在此基础上,输出子域对应截面的速度、压力、湍动能和耗散率。
1.2 计算流程设置
子域的进口、两侧和顶面均指定为速度边界,导入由整车模型输出对应截面的速度、湍动能和耗散率。出口指定为压力边界,导入由整车模型输出对应截面的压力、湍动能和耗散率。地面和轨道给定为移动边界,移动速度为350 km/h。
采用STARCCM+软件的分离式求解器进行计算。参考TB/T 3503.4—2018的建议方法,并结合本研究,对计算流程设定如下:① 首先采用不可压SSTk-ω模型迭代1 500步,然后更换成可压SSTk-ω模型继续迭代1 500步,以得到稳定的流场;② 选用iDDES进行非定常计算。由于车厢连接处的脉动压力主要发生在几十赫兹的低频段,为了在有限的计算资源和较短的计算时间内能够采集到足够长的压力信号,将时间步长设为0.002 s;③ 采用隐式计算方法,以避免产生时间步长对应的柯朗-弗里德里希斯-列维数大于1的情况发生,计算的时间和空间离散格式均为二阶;④ 当非定常计算物理时间达到2 s时,发现监控点的脉动压力达到动态平衡;⑤继续进行非定常计算,并开始采集车厢连接处的表面压力和空间压力,采集时间为2 s。采集得到的数据将用于分析车厢连接处的脉动压力特性。
1.3 计算结果分析
如图3所示,在上、下缺口分别以150 mm间距创建3个空间测点,分别依次命名为P1-1、P1-2和P1-3,P2-1、P2-2和P2-3。其中:P1-1和P2-1分别靠近上、下缺口前端;P1-3和P2-3分别靠近上、下缺口末端。
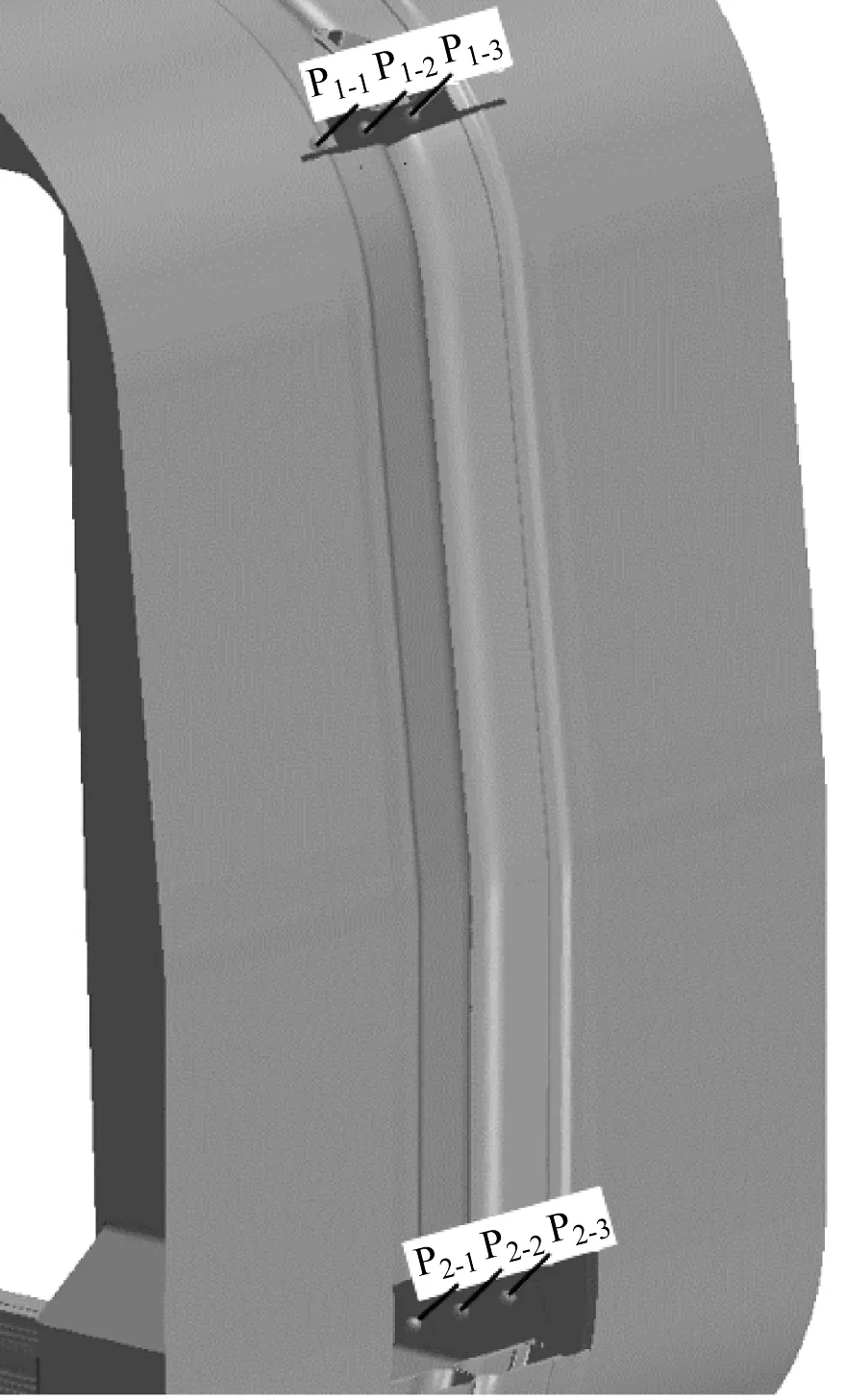
图3 车厢连接处测点布置图Fig.3 Layout of inter-coach test points
图4为各测点的压力功率谱密度图。从图4可以看出,压力脉动主要能量集中在50 Hz以下。P1-1的压力峰值小于P1-3的压力峰值,这是由于车厢连接处长度与深度的比值较小,气流从前端分离,涡流逐渐向末端发展和扩散,呈现出开式空腔的流动形态。P1-3分别在频率为24 Hz、38 Hz和45 Hz时出现明显的峰值,但P2-3仅在39 Hz时出现明显尖峰。缺口区域气流分离形成的射流剪切层虽然存在多个频率成分,但并非每个频率都会引起强烈的气动噪声,只有那些自身能量大且与声腔模态频率一致或接近的频率才会因共振而产生气动噪声问题。
提取车厢连接处端墙和内、外风挡形成的声学空腔区域并建立声学网格,使用ACTRAN软件对此区域进行声学模态计算。声学模态计算的最高频率与流场计算的最高频率相同,均为250 Hz。为了保证最高频率对应波长有20个节点,模型的面网格和体网格最大尺寸均为68 mm,总声学网格数约为14万个。经计算,该声学空腔的1~5阶模态频率依次为24 Hz、40 Hz、58 Hz、75 Hz和96 Hz。通过对比射流剪切层频率和声学模态频率可知,40 Hz附近的射流剪切层频率会引起车厢连接处的共振,进而产生强烈的气动噪声。因此,乘务员室的噪声问题主要是车厢连接处发生了共振,共振频率在40 Hz附近。后续的优化重点为降低40 Hz附近的脉动压力。
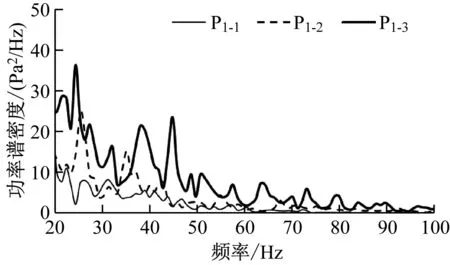
a) 上缺口测点
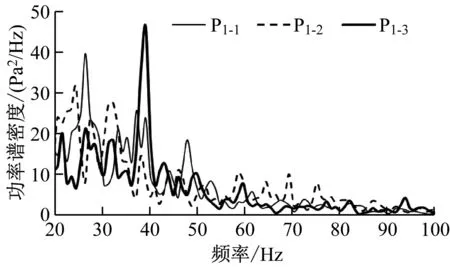
b) 下缺口测点图4 各测点的功率谱密度-频率曲线Fig.4 Power spectral density-frequency curve of each test point
2 脉动压力控制
2.1 控制方案
2.1.1 波浪板控制方案
将上文所述的尚未采取控制措施时的模型定义为基础模型。当前脉动压力控制主要为外形优化、被动流动控制和主动流动控制。在本车型车厢连接处通过外形优化来控制脉动压力,其控制效果不大。考虑到车厢连接处与转向架舱都有类似的空腔结构,结合近年在1∶3和1∶8压缩比例下高速列车转向架气动噪声控制的风洞试验所积累的经验,以及本车厢连接处具体结构,确定在上、下缺口两端采用波浪板进行车厢连接处的脉动压力控制。波浪板向外倾斜5°;下缺口板的长度和宽度分别为217 mm和281 mm,波高和波距分别为50 mm和70 mm;上缺口梯形板的短边和长边的长度分别为127 mm和229 mm,梯形板高为105 mm,波高和波距分别为50 mm和72 mm。
2.1.2 射流控制方案
主动射流近年来被尝试用于航空领域的气动噪声控制,但目前并未应用于高速列车领域中。为了评估射流在车厢连接处脉动压力控制的效果,本文尝试在上、下缺口两端布置射流器,以满足高速列车头尾互换的运行工况。上、下缺口射流器的宽度分别为132 mm和302 mm,高度均为20 mm。模拟时采用105 km/h(约0.3倍车速)的射流速度,射流方向与气流方向相同[10]。
2.2 控制效果分析
分别选取P1-3、P2-3,对比2个方案下各测点的压力功率谱密度变化情况,如图5所示。从图5中可知,采用波浪板方案后,多数频率下所对应能量均有显著降低。对以40 Hz为中心频率、带宽36~45 Hz各测点的脉动压力总能量进行计算,发现上缺口测点的脉动压力总能量由152 Pa2降至105 Pa2,下缺口测点的脉动压力总能量由171 Pa2降至71 Pa2;射流方案的降噪效果更好,开启射流后,上、下缺口测点的脉动压力总能量分别降至1 Pa2和15 Pa2。
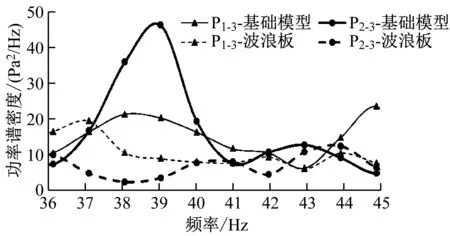
a) 波浪板方案与基础模型的对比
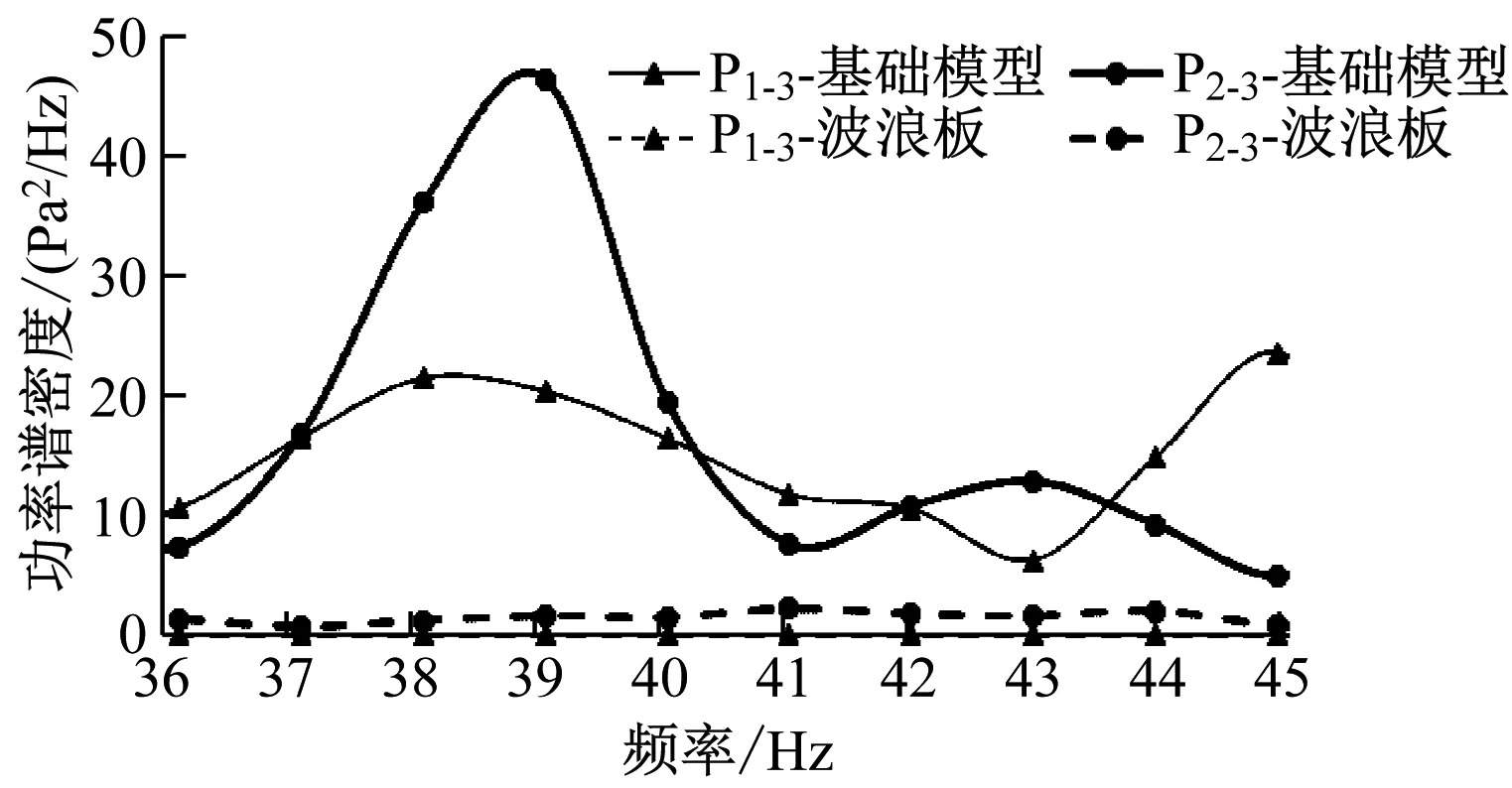
b) 射流方案与基础模型的对比图5 波浪板方案、射流方案与基础模型的 功率谱密度-频率曲线对比
虽然射流方案降噪效果好,但是在高速列车车厢连接处实施的难度很大。为此,本文仅在线路上测试时进行增加了波浪板控制方案,测试结果如图6所示。由图6可知,中心频率为40 Hz的声压级由105.0 dB降低到100.0 dB,降低了5.0 dB。其他频率的声压级也有不同程度的降低,车内总声压级由106.5 dB降低到102.5 dB,降低了4.0 dB,可见波浪板控制方案的降噪效果较好。

图6 波浪板方案和基础模型在不同频率下的声压级对比
3 结语
本文建立了含内、外风挡和端墙的车厢连接处的子域仿真模型,建立了8节编组列车的实车气动仿真模型,计算得到对应截面的速度、压力、湍动能和耗散率等参数,以作为子域的边界条件,采用延迟分离涡模型完成车厢连接处脉动压力的计算。经计算可知,由上、下缺口射流剪切层频率和车厢连接处所围区域的声腔的二阶声学模态频率接近,从而产生共振,这是高速列车上车厢连接处附近的乘务员室噪声过大的主要原因。
为解决此问题,本文提出了基于波浪板的被动流动控制方案,减弱了上、下缺口流动分离,降低了上、下缺口末端脉动压力和40 Hz所覆盖带宽的脉动压力总能量。实测结果表明:波浪板控制方案能使中心频率40 Hz的声压级降低5 dB,使车内的总声压级降低4 dB。
本文进一步提出了基于射流的主动流动控制方案,并对该方案进行了评估。射流方案相当于在缺口部位增加气幕,以起到屏障和遮挡作用,可显著减少缺口区域的平均涡量及测点在40 Hz所覆盖带宽的脉动压力总能量。因该方案的实施难度大,本文并未在线路进行实际测试,但根据外部脉动压力的降低量,可以预测该方案应该能降低车内噪声,并有望在未来成为可实施的方案。
——以徐州高层小区为例