低速磁浮线轨道钢箱梁表面温度分布及竖向挠度实测研究*

刘鸣博 叶 丰** 曾国锋 龚俊虎

(1.同济大学磁浮交通工程技术研究中心， 201804， 上海； 2.西南交通大学牵引动力国家重点实验室， 610031，成都； 3.中铁磁浮交通投资建设有限公司， 430060， 武汉∥第一作者， 硕士研究生)

国内外研究者对桥梁结构在太阳辐射作用下的温度效应及其分析方法等做了大量研究。文献[1]将桥梁结构温度场的研究方法分为理论分析、数值模拟及试验测试等3类；文献[2]建立了上海高速磁浮示范运营线钢箱梁的日照温度场模型，以缩尺模型的实测数据对模型进行验证后，计算了不同支承形式钢轨道梁的温度变形；文献[3]用傅里叶曲线拟合并研究均匀温度与波动温度的时程曲线，得到磁浮混凝土轨道梁温度场的时变规律；文献[4-6]以实际测试的数据为基础，利用威布尔和正态分布的加权模型拟合实测温差的统计结果，并据此推算最不利温差值；文献[7]引入赤池和贝叶斯信息判别准则，确定最优高斯分量数，建议采用分段函数来描述钢箱梁日温度变化特征。

与其他城市轨道交通制式相比，低速磁浮轨道梁在温度梯度作用下的挠度限值更为严格，目前尚无明确的针对低速磁浮轨道梁的温度梯度荷载规定或可借鉴的相关规范。CJJ/T 262—2017《中低速磁浮设计规范》中规定梁体在温度梯度作用下跨中竖向挠度的容许值为计算跨度的1/6 200，但未明确该规范值对应的温度梯度荷载作用。本文以上海临港低速磁浮线钢箱梁的表面温度监测数据为研究案例，对低速磁浮钢箱梁的表面温度分布及竖向挠度进行分析。

1 案例钢箱梁的现场测试概况

上海临港低速磁浮线的钢箱梁结构形式如图1所示。两侧F轨为列车无接触运行时的轨道，因其横断面形状类似字母F，故以“F轨”代称。钢轨枕将F轨连接成轨排，轨排通过钢箱梁顶面间隔布置的承轨台与钢箱梁连接。列车运行时，荷载由F轨向下依次传递至方钢管、混凝土承轨台以及钢箱梁上。钢箱梁表面无铺装保护，轨排可能会对钢箱梁顶面的日照有少许遮挡作用。

图1 上海临港低速磁浮线钢箱梁结构

本文选取上海临港低速磁浮试验线上47#～48#墩柱之间的钢箱梁进行现场温度测试。该钢箱梁为简支结构，跨度为25.0 m，高度为2.1 m。现场温度测点布置如图2所示，其中：A2-B2断面为跨中断面，被命名为断面2;其两侧的竖向断面A1-B1、A3-B3分别被命名为断面1和断面3。

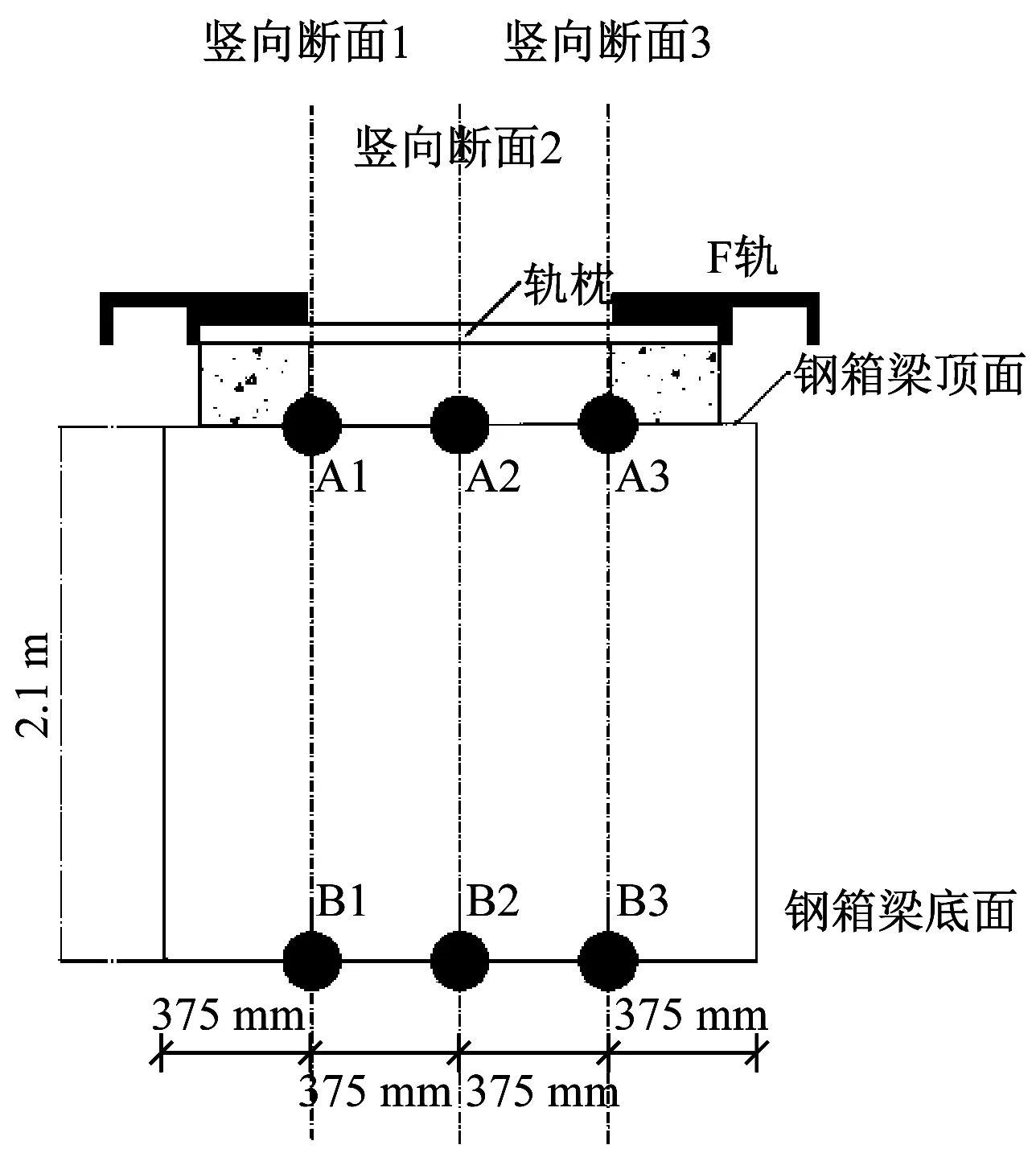
图2 钢箱梁测点布置示意图Fig.2 Diagram of steel box girder measurement points arrangement

2 竖向表面温度差分析

2.1 竖向表面温度差极值分析

对2020-07-30至2021-02-20期间该钢箱梁的表面温度进行监测，采样的时间间隔为15 min/次。选取2020-07-30至2020-09-03、2021-01-22至2021-02-20期间的监测数据作为钢箱梁表面温度差的统计分析样本。

将顶面测点监测值减去对应竖向断面上底面测点的监测值，得到的差值定义为该断面的竖向表面温度差。既有的研究表明，钢箱梁的正、负温差的统计特性具有较大的差异，因此本文对正、负温差进行了分类分析，设Tj为对应的竖向断面(j=1、2、3)的温度差样本，ΔTj为对应的温度差样本，ΔTj,p为Ti的正温度差，ΔTj,n为Tj的负温度差。在3个确定的竖向断面温度差的基础上，为反映钢箱梁顶、底面间整体的温差特征，将梁顶面3个测点监测值取均值，减去同一时刻梁底面3个测点的平均监测值，将差值定义为平均表面温度差。将平均表面温度差样本表示为Ta，将平均表面正、负温度差样本分别表示为ΔTa,p和ΔTa,n。

图3为典型样本下钢箱梁各断面表面温度差及平均表面温度差的时程变化情况，可以看出：不同的温度差样本在时程波形上相似，但数值有所差异。T2的表面温度差变化最大，Ta与T3的表面温度差较为接近。

图3 典型样本下钢箱梁竖向表面温度差时程曲线

统计各断面监测样本的表面正、负温度差极值，结果如表1所示。由表1可知：① 竖向正温度差最大值为19.8 ℃，发生在断面2；负温度差最大值为-7.6 ℃，发生在断面1；断面3的表面温度差的极值统计结果与平均表面温差接近；② 4个温度差样本的表面负温度差绝对值均在4 ℃以上。

表1 各监测断面表面温度差样本极值

2.2 竖向表面温度差概率统计

过往的研究表明，威布尔分布模型、正态分布模型与钢箱梁的实测温差概率统计特征接近[4-6]。因此，本文采用多概率密度函数加权的形式拟合竖向表面温度差。通过观察实测数据的概率统计特征，将钢箱梁的表面温度差数据拆分为正、负温差样本，分别选取双威布尔分布模型、双正态分布模型、威布尔分布和正态分布加权模型进行比选，采用最小二乘法拟合确定最佳的参数取值，通过比较不同拟合结果的残差平方和得到最优的概率模型。图4为平均表面正、负温度差的拟合结果。

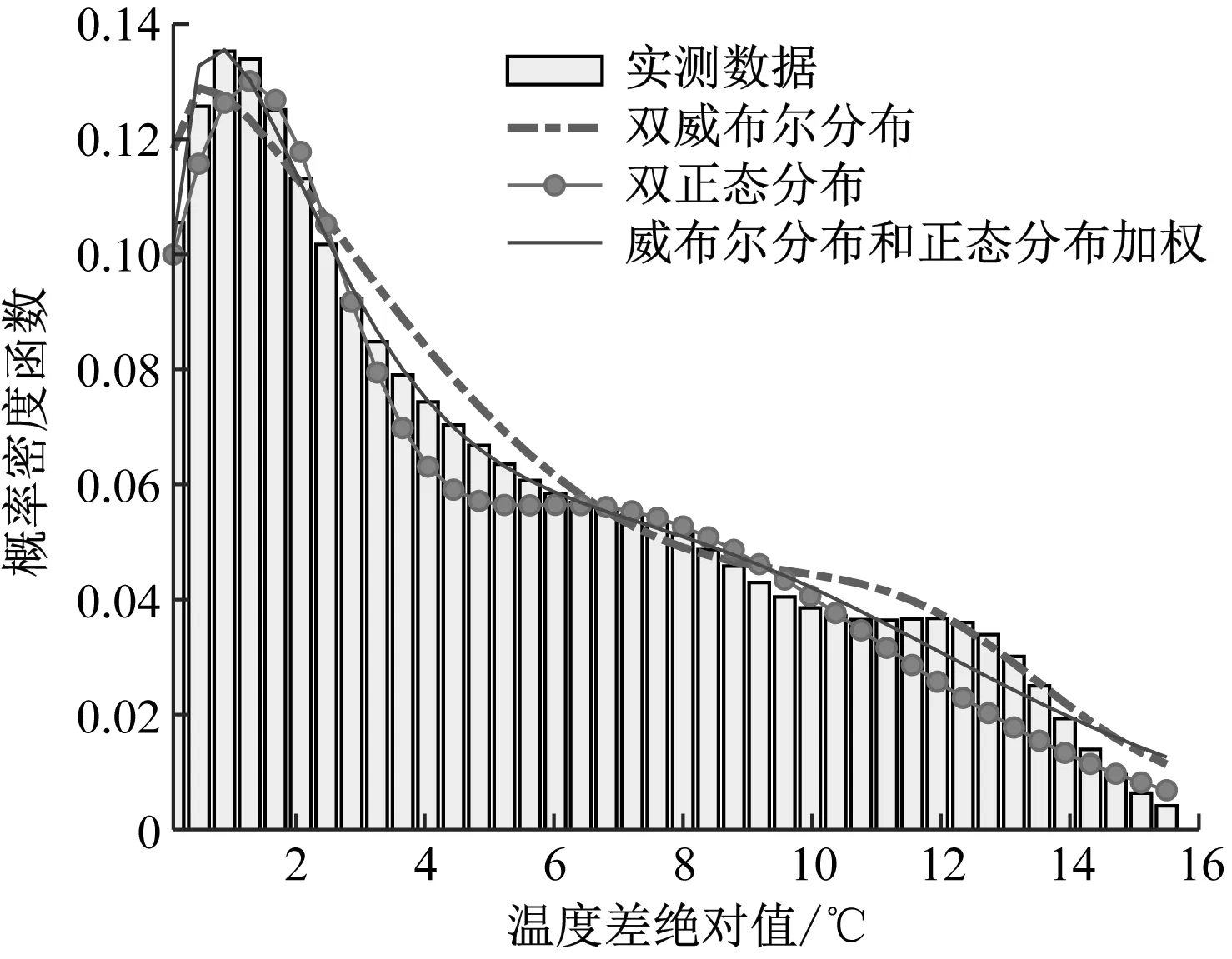
a) 表面正温度差拟合结果

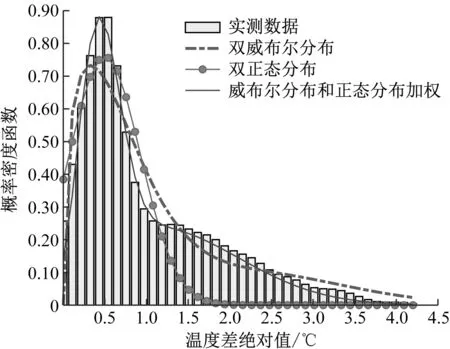
b) 表面负温度差拟合结果图4 平均表面正、负温度差拟合结果对比Fig.4 Fitting results comparison between surface positive and negative temperature difference

由计算结果可知：在描述各个样本的竖向表面温度差时，威布尔分布与正态分布加权模型的拟合效果最优，其总体的残差平方和最小。故最终选用威布尔分布与正态分布加权模型来描述低速磁浮轨道钢箱梁表面正、负温度差的概率统计特征，其计算式为：

g(ΔTi,p)=γ1W(ΔTi,p,α1,β1)+γ2N(ΔTi,p,μ1,λ1)

(1)

g(ΔTi,n)=ρ1W(ΔTi,n,α2,β2)+ρ2N(ΔTi,n,μ2,λ2)

(2)

式中：

g(ΔTi,p)、g(ΔTi,n)——分别为钢箱梁表面正、负温度差的概率密度模型；

β1、β2——威布尔分布的尺度参数；

μ1、μ2——正态分布的均值；

λ1、λ2——正态分布的方差；

α1、α2—— 威布尔分布的形状参数；

γ1、ρ1——威布尔分布的权重参数；

γ2、ρ2——正态分布的权重参数；

W(ΔTi,p,α1,β1)——变量为ΔTi,p、形状参数为α1、尺度参数为β1的威布尔分布函数；

N(ΔTi,p,μ1,λ1)——变量为ΔTi,p、均值为μ1、方差为λ1的正态分布函数；

W(ΔTi,n,α2,β2)——变量为ΔTi,n、形状参数为α2、尺度参数为β2的威布尔分布函数；

N(ΔTi,n,μ2,λ2)——变量为ΔTi,n、均值为μ2、方差为λ2的正态分布函数；

ΔTi——竖向表面温度差样本，包括ΔT1、ΔT2、ΔT3、ΔTa。

式(1)、式(2)满足γ1+γ2=1，ρ1+ρ2=1。式(1)中各参数的估计值如表2所示，式(2)中各参数的估计值如表3所示。

2.3 竖向表面温度差标准值分析

在重大工程的设计施工中，往往要计算具有一定重现期的标准值。气象研究中对重现期的计算一般转化为出现概率的计算，重现期为R年的极端值估计以1/(nR)对应的分位点处的数值表示，其中n为理论年样本总量。根据上文极端值分析的结论，本文偏保守地采用断面2对应的竖向表面正、负温度差样本的概率统计模型，用以计算温度差标准值的最大值和最小值。其概率分布函数可表示为：

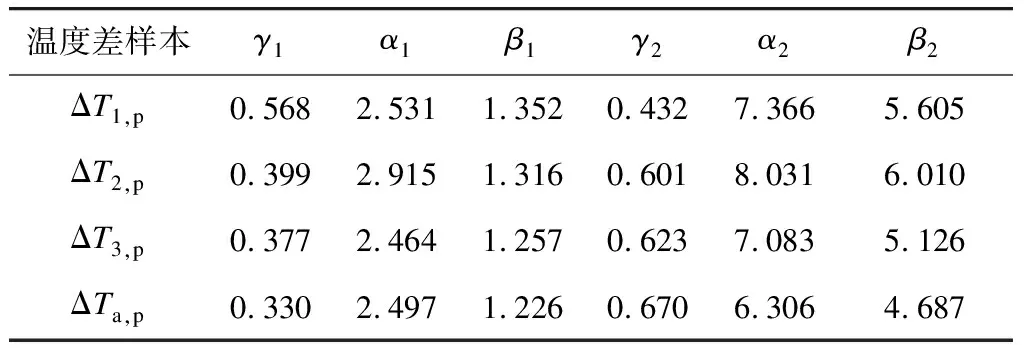
表2 正温度差拟合参数估计值

表3 负温差拟合参数估计值

F(ΔT2,p)=γ1FW(ΔT2,p)+γ2FN(ΔT2,p)

(3)

F(ΔT2,n)=ρ1FW(ΔT2,n)+ρ2FN(ΔT2,n)

(4)

式中：

F(ΔT2,p)、F(ΔT2,n)——分别为断面2的正、负温差变量的概率分布函数；

FW(ΔT2,p)，FW(ΔT2,n)——分别为变量是ΔT2,p、ΔT2,n的威布尔概率分布函数；

FN(ΔT2,p)、FN(ΔT2,n)——分别为变量是ΔT2,p、ΔT2,n的正态概率分布函数。

参照欧洲结构设计标准的相关规定，采用具有50年重现期(R=50)的温度差特征值作为标准值，选取数据的采样频率为15 min/次，则1 d的总采集次数为96次。取1年为365 d，故n=35 040。据此可计算得钢箱梁表面的正温度差标准值为29.2 ℃，负温度差标准值为-10.2 ℃。

3 等效线性温差与实测温差的关系分析

钢箱梁的竖向表面温度差的主要影响因素为日照。为减小降雨、强风等复杂天气因素的影响，本文选取监测期间晴好天气的温度及梁底竖向挠度数据的典型样本，如图5所示。

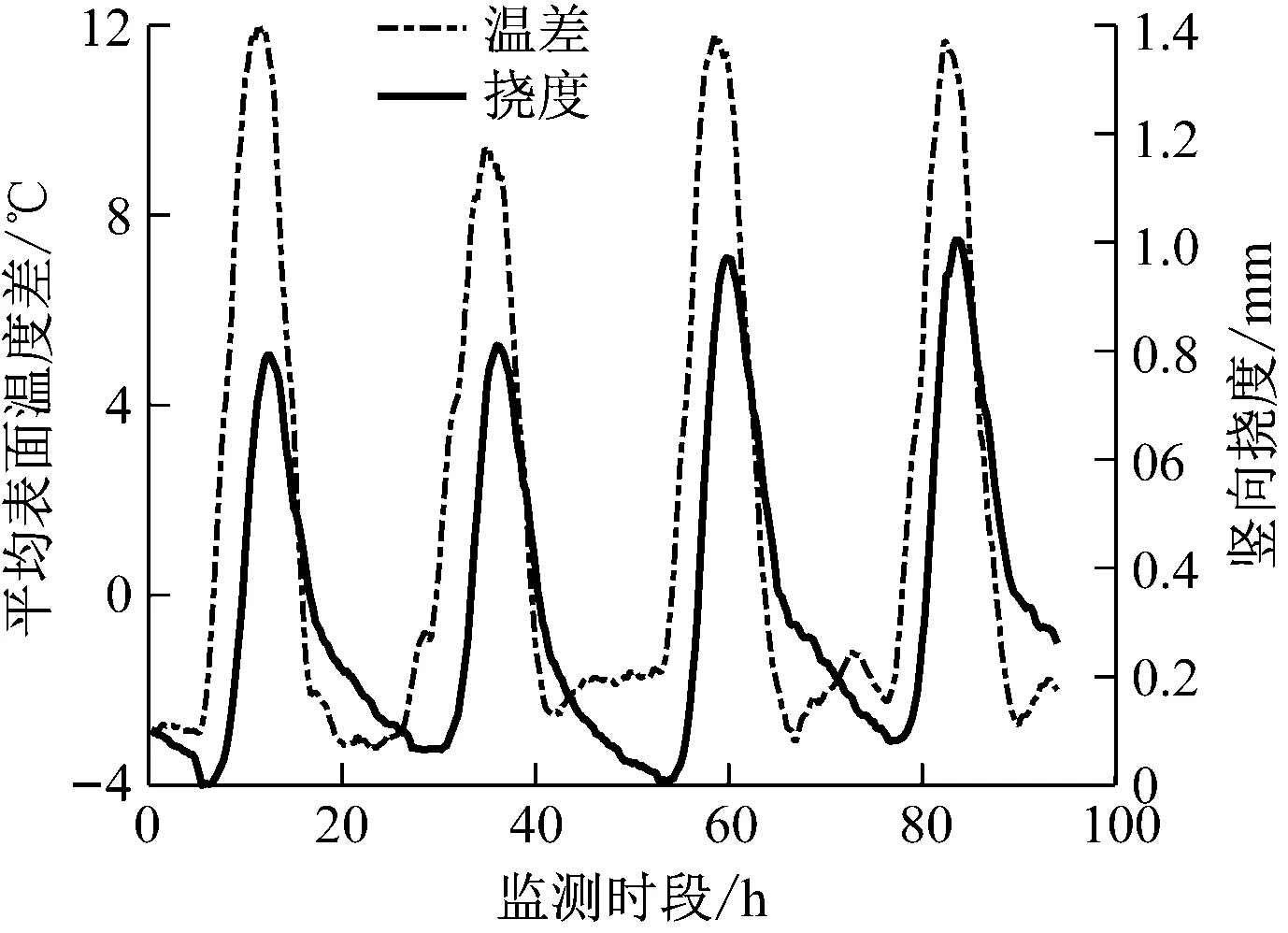
图5 典型样本下竖向挠度及平均表面温度差监测数据

由图5可知，钢箱梁的竖向表面温度差与梁底挠度之间存在较强的相关性，挠度与等效线性温差的换算关系式为：

(5)

式中：

Δtmax——挠度等效线性温差，℃；

h——钢箱梁的高度，m；

Δftmax——钢箱梁跨中竖向挠度值，m；

L——钢箱梁的长度，m；

θ——线膨胀系数，1/℃。

由图6的结果观察可知，实测温差与挠度的等效线性温差之间呈带状分布，基本可以认定钢箱梁的竖向表面温度差与梁底挠度的等效线性温差之间服从线性关系。考虑工程适用性，以线性模型描述钢箱梁表面的实测温度差与挠度等效线性温差间的关系，其计算式为：

ΔTequ=kΔTa+b

(6)

式中：

ΔTequ——与实测挠度值对应的等效线性温差；

k、b——待定系数。

通过最小二乘法求解得：k=0.12，b=-0.16。

由拟合结果可知：① 大部分实测值与拟合值之间的残差绝对值在1 ℃以内，且基本呈带状分布于拟合曲线的两侧；② 实测数据与拟合曲线之间的拟合残差绝对值最大值为2.7 ℃，由此引起的竖向挠度推算值的偏差对于低速磁浮线而言仍需要加以重视。为保证按此关系式计算的挠度推算值具备一定的安全余量，以覆盖100%的数据点为标准，调整参数b的取值至2.62，拟合得到的上限曲线如图6所示。

图6 实测数据散点分布与拟合曲线Fig.6 Scattered distribution and fitted curve of the measured data

由此可推算得到等效线性温差的估计值区间及等效挠度值的可能取值区间。结合上文得到的竖向表面温度差标准值，对等效温差极端值对应的竖向挠度进行估算，并与规范限值进行对比，如表4所示。由表4可知：① 针对高度为2.1 m的简支钢箱梁，由实测数据推算得到的50年重现期温度梯度产生的挠度标准值，满足中低速磁浮规范的要求；② 磁浮钢箱梁的竖向负温度差较大，其竖向负挠度不可忽略。

表4 温度差标准值及估计挠度值

4 结语

本文以上海临港低速磁浮试验线上的钢箱梁表面温度分布实测数据为案例，初步研究了钢箱梁表面温度差的概率分布特性和等效线性温差与实测温差间的关系，得到以下结论：

1) 可以通过威布尔分布与正态分布加权模型来描述低速磁浮钢箱梁顶面、底面的表面温度差概率密度特征。根据概率模型推算出具有50年重现期的钢箱梁竖向表面正温度差标准值为29.2 ℃，负温度差标准值为-10.2 ℃。

2) 本文主要考虑日照导致的温差影响。低速磁浮钢箱梁表面竖向挠度的等效线性温差与实测竖向表面温度差之间可以通过线性模型描述，并可通过包络的方式得到钢箱梁表面竖向表面温度差所对应的等效挠度取值范围。其中：正向(竖向向下方向)挠度的取值范围为1.96～2.86 mm，负向(竖向向上方向)挠度的取值范围为-0.86～-1.76 mm。

3) 因样本数量和测试对象具有局限性，本文针对低速磁浮钢箱梁温度场分布和效应的实测分析尚处于初步探索阶段。未来如能有更多试验梁的实测数据，必将有助于更好地总结规律，为低速磁浮钢箱梁结构设计提供参考。