CORS高程时间序列非线性趋势项模式识别与估计
张恒璟,王 蕾,金泽林,兰文琦,齐 昕
CORS高程时间序列非线性趋势项模式识别与估计
张恒璟,王 蕾,金泽林,兰文琦,齐 昕
(辽宁工程技术大学 测绘与地理科学学院,辽宁 阜新 123000)
针对传统线性模型拟合连续运行参考站(CORS)高程时间序列使测站运动趋势单一化的问题,提出一种基于CORS高程时间序列本身的非线性趋势项定量识别与估计方法。该方法首先用均值聚类整体经验模态分解方法,对CORS高程时间序列进行分解;其次,基于排列熵理论对非线性趋势项定量识别,统计决策适合的趋势项模型,并估计模型参数。实验结果表明:基于排列熵的非线性趋势项定量识别方法避免了人为判别误差,准确地反映了序列自身的变化趋势;通过比较傅里叶、正弦函数、线性多项式三种模型的拟合效果,发现傅里叶模型拟合效果最佳。
高程时间序列;趋势项;排列熵;模型拟合;定量估计
0 引言
传统的序列趋势项是由固定的模型拟合得出[1],经过拟合后能够得出序列的周期项、常数项、线性速率等信息。针对如地震、海啸、更换仪器等操作产生的序列影响,通常在固定模型的基础上,加入各项改正,采用最小二乘求解拟合参数,为后续时频分析提供基础。
国内外研究表明,连续运行参考站(continuously operating reference stations, CORS)高程时间序列是非线性非平稳的序列[2-5],全球范围内各个CORS所处地理位置不同、受到地球物理因素差异性的影响,导致各个CORS的运动趋势不完全相同,采用统一的趋势项拟合模型使各个CORS运动趋势单一化。且有研究指出[6-7],趋势项是一个基于序列自身存在的单调拟合函数,在长期时间序列趋势项识别中,应选择基于序列本身识别的方法。排列熵算法作为一种新颖的突变检测方法,可以检测动态突变和时间序列随机性,并定量评估信号序列中包含的随机噪声。其优点是:①计算简单,抗噪声能力较强;②该算法对时间敏感,可以实现高分辨率;③算法的输出结果直观,突变信息更易识别。依据该方法的独特优势,本文引入具有自适应性的均值聚类整体经验模态分解(-means clustering-ensemble empirical mode decomposition,-EEMD)算法,对CORS高程时间序列进行分解,结合趋势项定义和排列熵理论,对非线性趋势项进行定量识别与合成,解决了使CORS运动趋势单一化问题,更好地反映CORS运动趋势,丰富了CORS运动趋势提取方法。
1 K-EEMD与排列熵理论
1.1 K-EEMD算法
-EEMD是文献[8]针对整体经验模态分解(ensemble empirical mode decomposition, EEMD)信号分解时,信噪比低及模态混叠问题,所提出的一种改进的EEMD算法。该方法首先在EEMD分解前,向原始序列中随机添加白噪声;其次,引入统计学均值聚类思想,对EEMD算法100次迭代计算产生的本征模态函数(intrinsic mode function, IMF)分量矩阵,以欧氏距离作为相似程度判断依据,对IMF分量进行均值聚类分析,不断迭代直至聚类中心不再发生改变;最后,保留各IMF分量聚类簇中最多的一类结果取平均值作为最终IMF分量。实验结果表明,该方法获取了CORS高程时间序列中频率从高至低的IMF分量,减弱了EEMD算法的模态混叠现象,提高了信噪比,基本消除了EEMD算法得到的低频IMF分量中残留高频噪声的现象。
1.2 排列熵理论
排列熵(permutation entropy, PE)是一种通过计算时间序列的复杂性程度以及检验序列随机性和突变的方法。该算法设计概念简单,计算速度快,并且特别适用于非线性非平稳数据,表现出较好的鲁棒性[9-11],其理论如下:

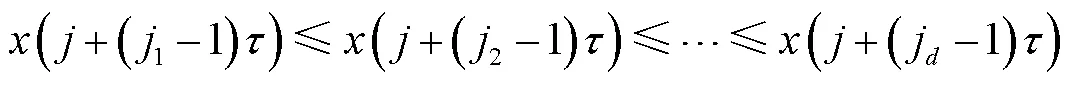
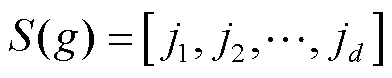
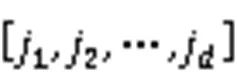


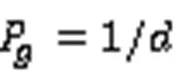
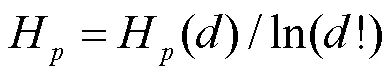

2 非线性趋势项定量识别与合成
利用国内外BJFS、SYDN、JOEN、HOB2站近20 a的高程时间序列进行实验。实验数据来自斯克里普斯轨道和常驻阵列中心(Scripps Orbit and Permanent Array, SOPAC)网站提供的原始(RAW)数据,利用四分位差法对原始数据进行粗差剔除后,采用三次样条插值法进行插值,已进行去均值处理。如图1所示,对四个站高程时间序列数据进行-EEMD实验,图1中仅给出中低频的IMF分量。
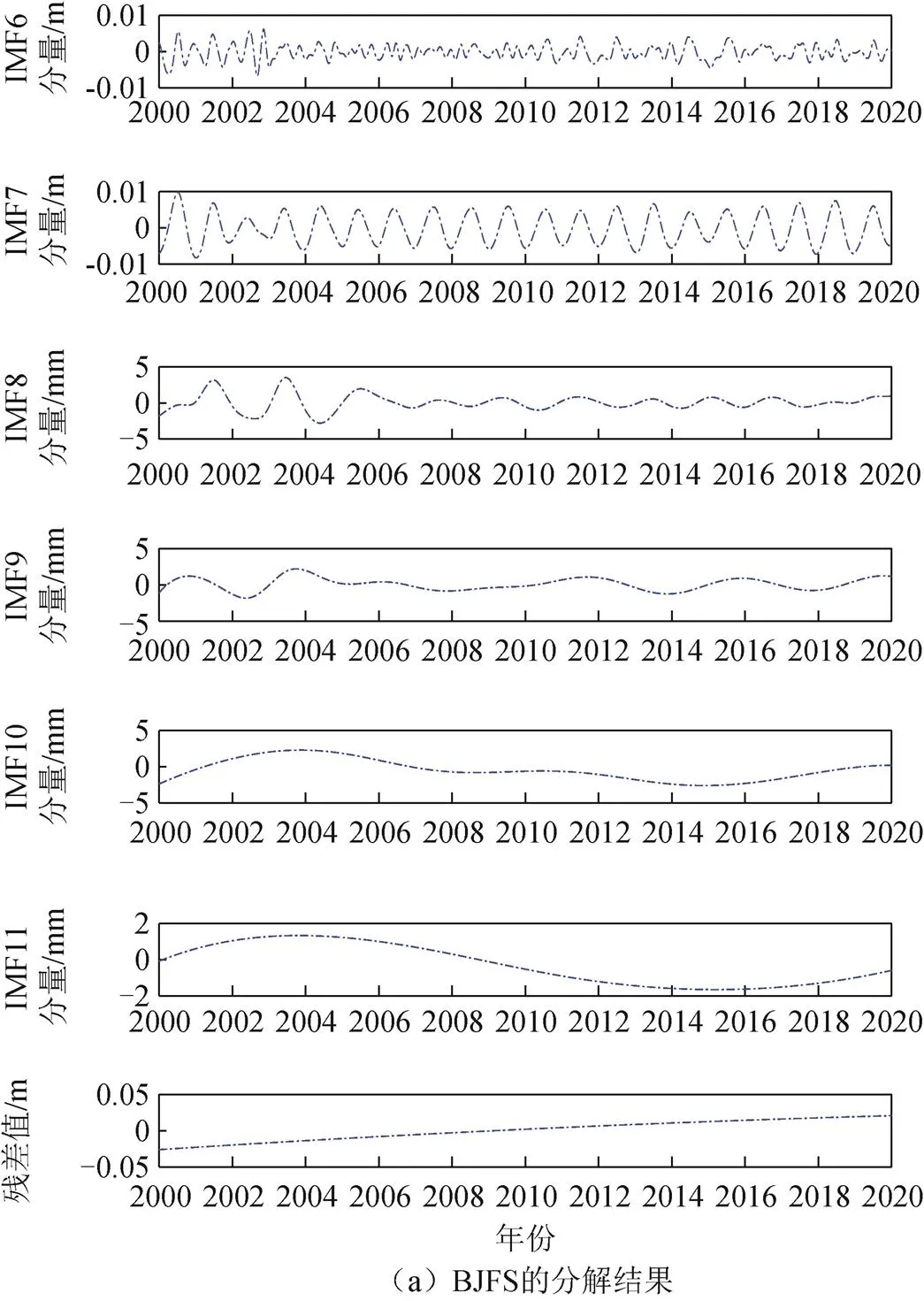
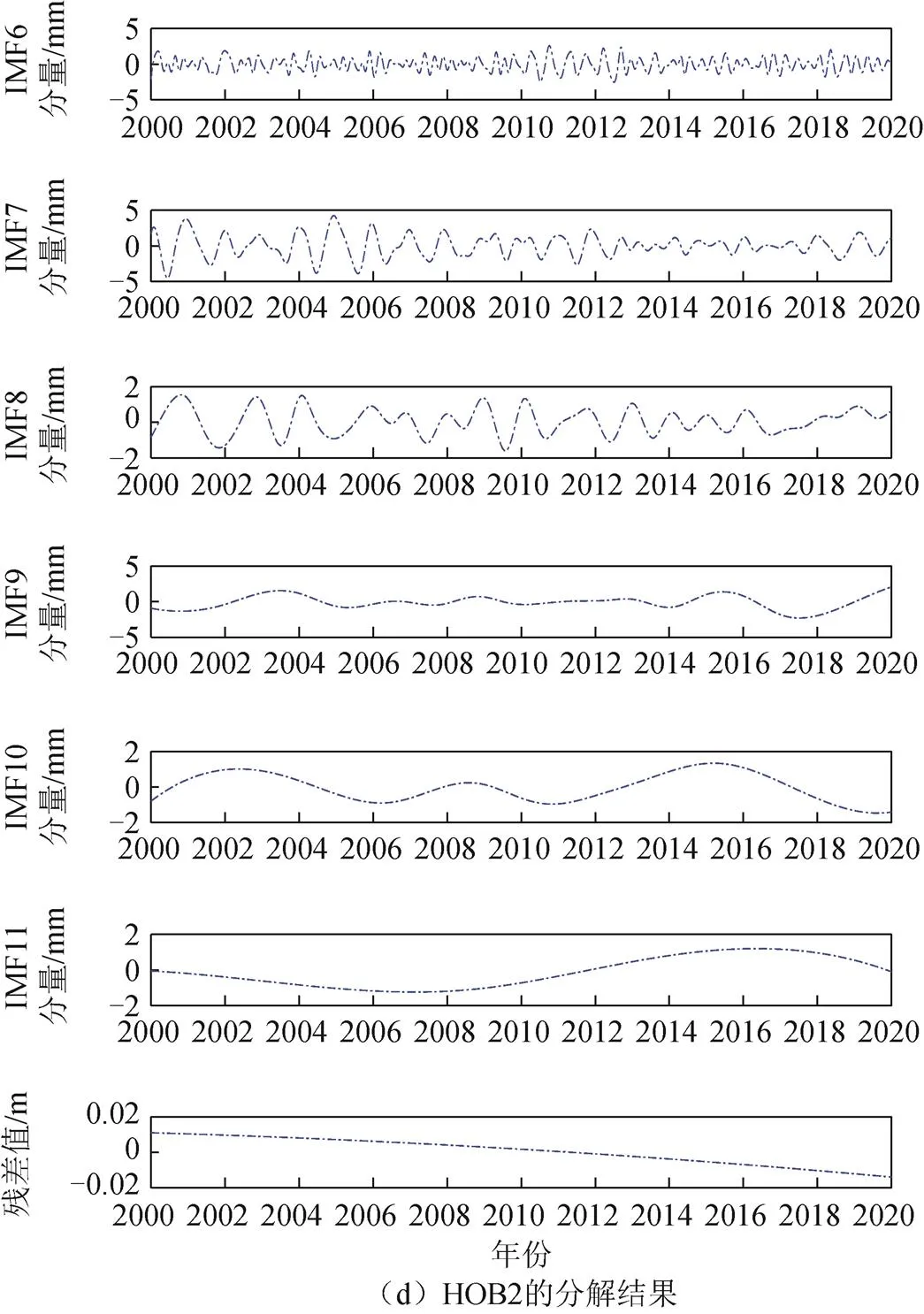
图1 K-EEMD分解部分IMF分量
经过-EEMD分解之后,残差值(residual)可作为各序列非线性趋势项的基础项,基础项呈现单调变化趋势。但在分解过程中,可能存在过度分解或者长周期项与趋势项无法识别的现象,此时可以进行趋势项合成实验[12],将低频IMF分量依次并入基础项,如图2所示。
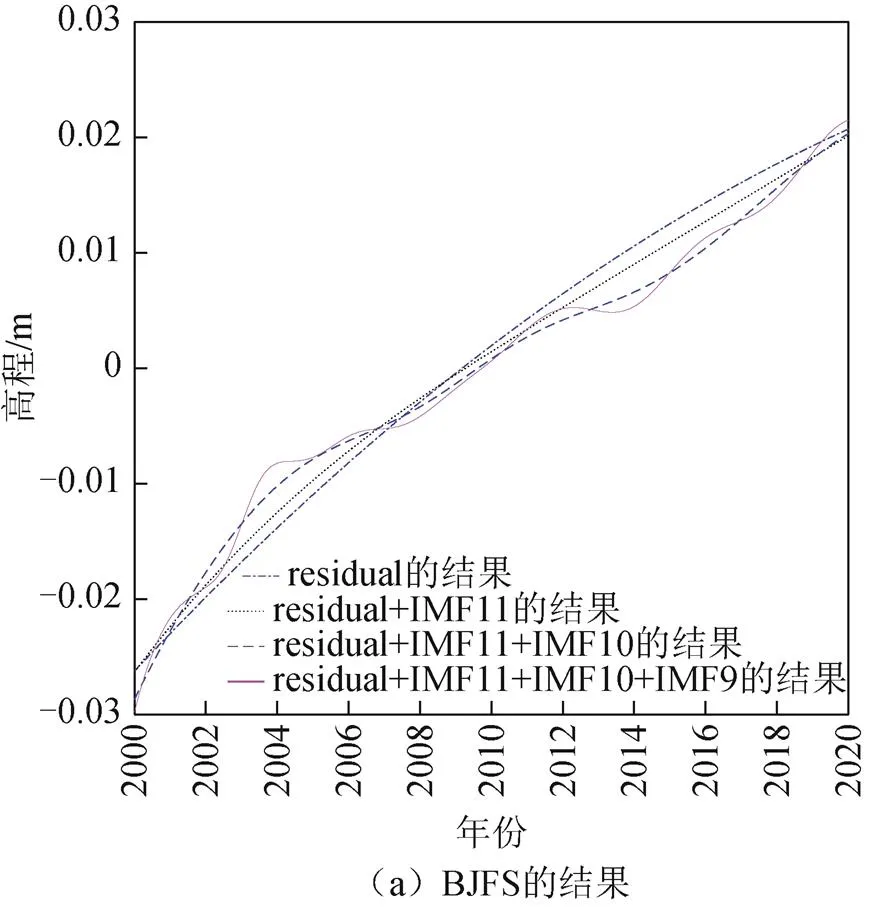
此时,可以采用人工判读对各合成项进行单调性判别,若合成趋势项满足单调特性,则将证明该IMF分量为趋势项;若产生周期运动趋势,则该IMF分量为当前时间尺度内无法识别的长周期项。
BJFS站加入IMF11、IMF10后,保持单调向上趋势,加入IMF9分量后,产生了周期震荡,即BJFS站的趋势项为residual+IMF11+IMF10,IMF9分量为长周期项;SYDN站加入IMF11后,保持单调向下趋势,加入IMF10后,无法准确判断其是否为单调变化,加入IMF9后,产生了周期震荡,即SYDN站的趋势项为residual+IMF11,IMF10无法确定,IMF9为长周期项;JOEN站加入IMF11、IMF10后,保持单调向上趋势,加入IMF9后则产生了周期震荡,即JOEN站的趋势项为residual+IMF11+ IMF10,IMF9为长周期项;HOB2站加入IMF11后,仍保持单调向下趋势,加入IMF10、IMF9后,产生了周期震荡,即HOB2站的趋势项为residual+ IMF11,IMF10和IMF9为长周期项。这种方法缺乏理论指导,且数据量大、较小数据变化在曲线图中无法表现,导致部分IMF分量无法准确判断,分别计算各站合成项的排列熵,排列熵统计结果如表1所示。

表1 排列熵统计
当排列熵为0时,原始序列相空间重构后排序固定,表示序列稳定严格单调变化,定量地判别了合成项的单调变化趋势。从排列熵指标不难看出:BJFS站的趋势项为residual+IMF11+IMF10;SYDN站趋势项为residual+IMF11+IMF10;JOEN站趋势项为residual+IMF11+IMF10,HOB2站趋势项为residual+IMF11。该方法与人工判别结论一致,同时能准确判别出SYDN站IMF10分量为趋势项的一部分。
排列熵指标显示,SYDN站余项并非严格单调变化,查看余项数据发现,其确实不为严格单调变化。这种现象可能是-EEMD分解的端点效应,加入IMF11后,趋势项严格单调变化,也证明了SYDN站的趋势项应该为residual+IMF11,而不是单纯以余项为该站趋势项。
3 非线性趋势项定量估计
通过定量识别和合成实验,得到了经过-EEMD分解的各个CORS非线性趋势项,结合趋势项定义选用三种模型:正弦函数模型、多项式模型、傅里叶模型对CORS非线性趋势项进行拟合。
1)线性多项式模型。在经典的时间序列拟合模型中,通常认为趋势项是一条直线,所以用线性多项式直接进行拟合,选取最小二乘进行逼近,求解线性方程的系数进而完成拟合。线性多项式的表达式为

2)正弦函数模型。通过本文-EEMD分解时间序列识别和合成趋势项后,每个CORS站都存在单调非线性趋势项,采用经典线性拟合方法可能会出现偏差,当三角函数的周期足够大时,在一定时间尺度上可以保持单调趋势,因此可以采用正弦函数对非线性趋势项进行拟合。正弦函数模型的表达式为

3)傅里叶模型。傅里叶拟合是一种通过傅里叶技术不断逼近数据的曲线拟合方法,可看做多个正弦函数和余弦函数叠加的过程,经过傅里叶变换,对曲线进行拟合。傅里叶模型的表达式为

采用3种拟合方法对4个CORS站高程时间序列拟合结果如图3所示,图3中离散点为SOPAC给出的各站运动趋势,实线为本文识别的该测站非线性趋势项,余下3种依次为正弦函数拟合、线性多项式拟合和傅里叶函数拟合结果。
从图3可知,当趋势项近似线性变化时,3种拟合模型拟合结果相近;当趋势项变化为非线性时,傅里叶拟合模型明显优于其他两种模型。为验证本文提取趋势项的正确性,将线性拟合结果与SOPAC给出的趋势项参考值进行比对,如表2所示。

图3 趋势项拟合

表2 线性拟合结果对比
对4个测站的非线性趋势项线性拟合效果进行观察,所有测站提取的拟合结果均在SOPAC给出的参考范围内,说明本文提出的非线性趋势项识别方法和识别结果是可靠的。为定量比较3种拟合方案的优劣性,采用均方根误差、拟合优度两种精度指标,进行拟合精度评定,其评定结果如表3所示。
1)均方根误差。反映了拟合估计值与真实值间的偏离程度,数值越小表示偏离程度越小。均方根误差的计算公式为
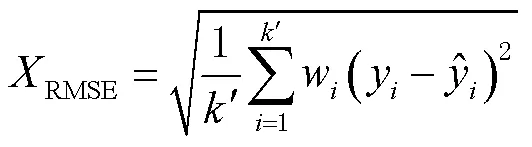
2)拟合优度。拟合优度表示拟合效果的好坏,越接近1代表该模型的拟合效果越好。拟合优度的计算公式为
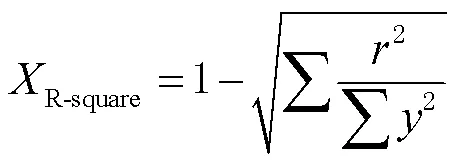

表3 拟合精度统计
分析表3可知:当测站趋势项为非线性时,傅里叶模型拟合效果最佳,正弦函数模型次之,线性多项式拟合效果最差;当测站趋势线接近线性时,3种拟合模型均有较好的拟合效果,但傅里叶模型拟合最佳。
4 结束语
针对传统线性模型拟合CORS站高程时间序列使测站运动趋势单一化的问题,本文结合-EEMD算法和排列熵,提出了一种基于CORS高程时间序列本身的非线性趋势项定量识别与估计方法。4个CORS站近20 a的高程时间序列实验结果表明:本文提出的CORS站高程时间序列非线性趋势项定量识别与估计方法,可以有效地识别并分离非线性趋势项,得到基于序列自身特性的单调拟合函数。
在研究过程中发现:相同区域的测站具有相似的运动特性,不同地区的测站间运动差异较大。下一步将结合测站所处地理位置对引起测站高程非线性运动的地球物理因素进行定量分析,获取各测站高程方向上更为准确的运动规律。
[1] 姜卫平. GNSS 基准站网数据处理方法与应用[M]. 武汉: 武汉大学出版社, 2017.
[2] 程鹏飞, 成英燕, 秘金钟, 等. 2000国家大地坐标系建立的理论与方法[M]. 北京: 测绘出版社, 2014.
[3] 张鹏, 蒋志浩, 秘金钟, 等. 我国 GPS 跟踪站数据处理与时间序列特征分析[J]. 武汉大学学报(信息科学版), 2007, 32(3): 251-254.
[4] 刘宗强, 党亚民, 杨强, 等. 顾及共模误差的四川连续 GPS 基准站坐标时间序列噪声分析[J]. 大地测量与地球动力学, 2018, 38(5): 510-515.
[5] 武曙光. 区域 CORS 站坐标时间序列特征分析[D]. 武汉: 武汉大学, 2017.
[6] HUANG N E, WU M L C, LONG S R, et al. A confidence limit for the empirical mode decomposition and Hilbert spectral analysis[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2003, 459(2037): 2317-2345.
[7] WU Z, HUANG N E. A study of the characteristics of white noise using the empirical mode decomposition method[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2004, 460(2046): 1597-1611.
[8] 张恒璟, 齐昕, 文汉江. 基于 K 均值聚类 EEMD 的 CORS 高程时间序列信号分析方法[J]. 大地测量与地球动力学, 2019, 39(10): 1053-1057.
[9] 郑近德, 程军圣, 杨宇. 改进的EEMD算法及其应用研究[J]振动与冲击, 2013, 32(21): 21-26.
[10] 雷亚国, 孔德同, 李乃鹏, 等. 自适应总体平均经验模式分解及其在行星齿轮箱故障检测中的应用[J]. 机械工程学报, 2014, 50(3): 64-70.
[11] 李长伟, 雷文平, 庞博, 等. 基于EEMD的相关排列熵的滚动轴承故障诊断[J]. 组合机床与自动化加工技术, 2020(8): 1-4.
[12] BANDT C, POMPE B. Permutation entropy: a natural complexity measure for time series[J]. Physical Review Letters, 2002, 88(17): 1-4.
Pattern identification and estimation of nonlinear trend items in elevation time series of CORS
ZHANG Hengjing, WANG Lei, JIN Zelin, LAN Wenqi, QI Xin
(School of Geomatics, Liaoning Technical University, Fuxin,Liaoning 123000, China)
Aiming at the problem that the traditional linear model fits the Continuously Operating Reference Stations (CORS) elevation time series to make the station movement trend singular, this paper proposes a quantitative identification and estimation method of nonlinear trend items based on the CORS elevation time series itself. This method first uses the-means clustering global empirical mode decomposition method to decompose the CORS elevation time series. Secondly, based on the permutation entropy theory, quantitatively identify the nonlinear trend item, make statistics on the trend item model suitable for decision-making, and estimate the model parameters. The experimental results show that the quantitative identification method of nonlinear trend item based on permutation entropy avoids human discrimination errors and accurately reflects the changing trend of the sequence itself. By comparing the fitting effects of Fourier, sine function, and linear polynomial models, it is found that the Fourier model has the best fitting effect.
elevation time series; trend item; permutation entropy; model fitting; quantitative estimates
P228
A
2095-4999(2022)02-0152-07
张恒璟,王蕾,金泽林,等. CORS高程时间序列非线性趋势项模式识别与估计[J]. 导航定位学报, 2022, 10(2): 152-158.(ZHANG Hengjing, WANG Lei, JIN Zelin, et al. Pattern identification and estimation of nonlinear trend items in elevation time series of CORS[J]. Journal of Navigation and Positioning, 2022, 10(2): 152-158.)
10.16547/j.cnki.10-1096.20220219.
2021-04-27
张恒璟(1982—),男,河南邓州人,博士,副教授,研究方向为空间大地测量数据处理与GNSS高程非线性运动。
王蕾(1997—),男,安徽阜阳人,硕士研究生,研究方向为空间大地测量数据处理。

