基于三层数据挖掘和遗传算法的大学生体质评价模型

陈兴 马致明

摘要：针对现存的大学生综合体质评价模型在不均衡数据集下泛化能力受限问题，提出了一种基于三层数据挖掘和遗传算法的体质评价模型。从身体形态、身体素质和身体机能三个方面出发，构建了包含八个测量指标的学生体质评价指标体系。依照评价指标采集相关数据，利用数据挖掘技术中的K-means、Apriori和ACI构建三层数据挖掘结构，基于遗传算法优化过程对指标数据进行训练，输出学生体质评价结果。与近年来在体质预测研究中相对优异的3个模型作为基准模型进行对比，实验结果表明，该模型能够有效地提高泛化能力，宏F1、准确率分别达到81.73%、89.47%，均优于基准模型。

关键词：大学生体质预测;不均衡数据集;三层数据挖掘;ACI算法;遗传算法

中图分类号：TP311;G804.49      文献标识码：A

文章编号：1009-3044（2022）05-0017-03

1 引言

目前，我国学生体质健康面临着不断下滑的严峻形势，党和国家高度重视学生体质健康，利用简单的测量指标判断学生体质状况，有助于进一步调整干预措施[1]，改善学生体质状况，达到体质监测的目的。因此，构建精度高、稳定性强的学生体质评价模型具有十分重要的意义。

数据挖掘技术能够在海量的、含噪的、缺失的数据集中发现隐藏在数据中的规律[2]，且遗传算法作为一种高效的全局搜索方法，在组合优化方面表现出色[3]，可有效解决普遍使用单一数据挖掘技术在不均衡数据集下模型泛化能力受到限制的问题[4-6]。基于此，本文提出了基于三层数据挖掘和遗传算法的体质评价模型，为大学生体质预测提供了新的思路和方法。

2 基于数据挖掘和遗传算法的体质评价模型构建

2.1 相关术语

设数据集的属性集合A={ ai | i=1，2，3，…，n}，ai∈{ vij | j=1，2，3，…，m}，其中vij是属性ai的值。

项：由属性和属性值构成，用“ai = vij”表示。

项集：由两个及以上个项组成的集合，如 a1 = v13 ∧ a2 = v21 ∧ a3 = v32。

关联规则：由两部分组成，左部和右部均是项或项集，且左部与右部相对应的属性集合互斥，如a1 = v13 ∧ a2 = v21 ∧ a3 = v32 → a4 = v41 ∧ a5 = v51。

关联分类规则：一种特殊的关联规则，左部为不包含标签属性的项或项集，右部为包含标签属性的项，如a1 = v13 ∧ a2 = v21 → a3 = v32，其中a3为标签属性。

覆盖[7]：如果一个实例d满足关联规则r的限制，即规则r中的属性集合是实例d的属性集合的子集，且规则r属性的取值与实例d属性的取值一致，则称规则r覆盖实例d。

2.2 建立评价指标体系

为了全面地、高精度地对学生体质进行评价，采用《国家学生体质健康标准》[8]（以下简称《标准》）要求的评价指标，构建由身体形态、身体素质和身体机能三个方面的学生体质评价指标体系，如图1所示。

身体形态反映生长发育状况和体质水平的重要方面，身高和体重是最直观的指标。身体素质是指人体机能通过肌肉活动所表现出来的基本活动能力，是评价人体运动能力和健康状况的重要指标，衡量指标有50米跑、坐位体前屈、立定跳远、800米跑和仰卧起坐。身体机能是人体在新陈代谢作用下，各器官系统工作的能力，衡量指标为肺活量[9]。

综合评价分数采用100分制形式，不低于90分为优秀，80.0～89.9分为良好，60.0～79.9分为及格，59.9分及以下为不及格。女生体测数据（部分）如表1所示。

2.3 三层数据挖掘结构

大学生体质测试各项指标成绩均为非连续型数据点，首先需要将各类指标进行离散化。考虑到按照《标准》规定的各指标區间划分是人为划定，较难体现数据本身的分布特性以及影响挖掘出有效的关联规则，因此采用无监督学习中的K-Means均值聚类算法对源样本进行预处理，分好对应的簇后，按照指定的规则对各簇中的样本进行编码，聚类和自编码后得到样本库，完成第一层数据挖掘。

然后，利用Apriori关联规则算法从样本库中找到满足支持度和置信度预设条件的强关联分类规则，完成第二层数据挖掘。本文规则的生成与传统的Apriori算法有所不同，在生成关联规则时，进行筛选，若关联规则是关联分类规则，则保存;否则，忽略掉。

最后，使用ACI算法[10]构建体质评价模型，完成第三层数据挖掘。将生成的规则根据支持度、置信度按升序进行排序之后， ACI根据每个类预先设定的规则覆盖数阈值，对每条规则r进行遍历和选择：遍历训练集的每个实例d，当规则r覆盖实例d，规则r的覆盖数加1。若规则r的覆盖数为0，则删除规则r;否则，当覆盖实例d的规则数超过其对应类的阈值，则删除实例d。

2.4 遗传算法优化模型

遗传算法应用十分广泛，使用遗传算法优化得到结果不依赖于初始条件，且为全局最优解，具有较强的鲁棒性。因此，本文使用遗传算法对三层数据挖掘结构中的参数进行优化，得到体质评价模型，如图2所示。

遗传算法在体质评价模型中优化的过程为：首先对初始化参数进行编码，然后通过选择、交叉、变异操作产生适应度高的个体，接着进行迭代，直至达到预定的效果。

1）个体编码是遗传算法解决三层数据挖掘结构优化问题的第一步，需要根据参数特点进行设计，本文采用十进制编码方式，个体代表一组最优参数。

2）初始种群生成，本文采用遗传算法随机方式产生初始种群，即三层数据挖掘结构优化方案的可行解集合，这样的种群保证了多样性，有利于获得模型最优的参数。

3）建立适应度函数，适应度函数决定着种群的进化方向，通常使用错误率作为适应度函数，由于研究的对象是不均衡数据集，因此本文在常规的错误率计算中添加了代价系数，具体如式（1）所示。

[f=1ni=1nωjIyi=j#]                        （1）

其中：

[Ix=0，  x=true1，  x=false]

式（1）中，n为样本数，yi表示预测结果，j表示真实标签，ωj表示标签j预测错误的代价系数。

4）选择策略的确定，轮盘赌策略在遗传算法中常表现出非常好的收敛效果，稳定性好，因此本文采用轮盘赌策略选择部分优秀个体直接进入下一代种群。

5）交叉和变异操作的确定，根据三层数据挖掘结构优化问题的特点，本文采用均匀分布交叉方式和均匀变异方式。

3 仿真测试的结果与分析

3.1 数据集

本文收集了河南某所大学2019年和2020年在校女大学生体测成绩，共33220条记录，其中综合成绩为优秀有452条记录，良好有11021条记录，及格有20785条记录，不及格有962条记录。由于实验数据集是不均衡的，用一般随机取样法可能选不出少数类样本，因此本文分别从各类的样本中随机选出80%作为训练集，20%作为测试集。

《标准》中未单独对体重和身高给出评分，需计算BMI从而得到体重和身高的评分。实验中将BIM、肺活量、50米跑耗时、立定跳远、坐位体前屈、800米跑耗时、一分钟仰卧起坐均以K-Means聚类算法分为4簇，如表2所示。

3.2 评估准则

对于不均衡数据集训练出来的模型在训练中可能会将少数类样本作为噪音，仅使用准确率作为评估准则，会表现出假的高性能，且本实验研究的是多分类任务，因此采用宏F1（macro-F1）和准确率（Accuracy）来度量模型的性能，相关公式如式（2）、式（3）。

[macro-F1=1ni=1nF1i#]              （2）

[Accuracy=i=1nTPii=1nTPi+FPi#]                      （3）

其中，F1i表示第i類的F1值，TPi表示第i类将正例预测为正例的个数，FNi表示第i类将负例预测为正例的个数。

3.3 实验参数

为产生高质量的关联分类规则候选集，增加收敛速度，提高模型的泛化性能，实验设置最小支持度为0.1%，最小置信度为0.6，遗传算法的种群为30，最大进化代数为50，交叉概率为0.7，变异概率为0.2，收敛趋势如图3所示。

分析图3得到，本文模型在进化到12代时，适应度不再发生变化，遗传算法完成了模型优化。

3.4 实验分析

为了验证本文模型的有效性，选用近年来在体质预测研究中相对优异的3个基准模型，模型如下：

1）朴素贝叶斯（Bayes）：由文献[4]提出的基于朴素贝叶斯分类算法的预测模型。

2）GA-BP：为提升BPNN模型的性能，文献[6]提出了基于遗传算法优化的BPNN模型。

3）GABP-AdaBoost：考虑到集成学习的AdaBoost算法对训练集中分类错误的实例增加权重，从而提高模型预测效果，将GA-BP神经网络作为基分类器，构建GABP-AdaBoost 预测模型。

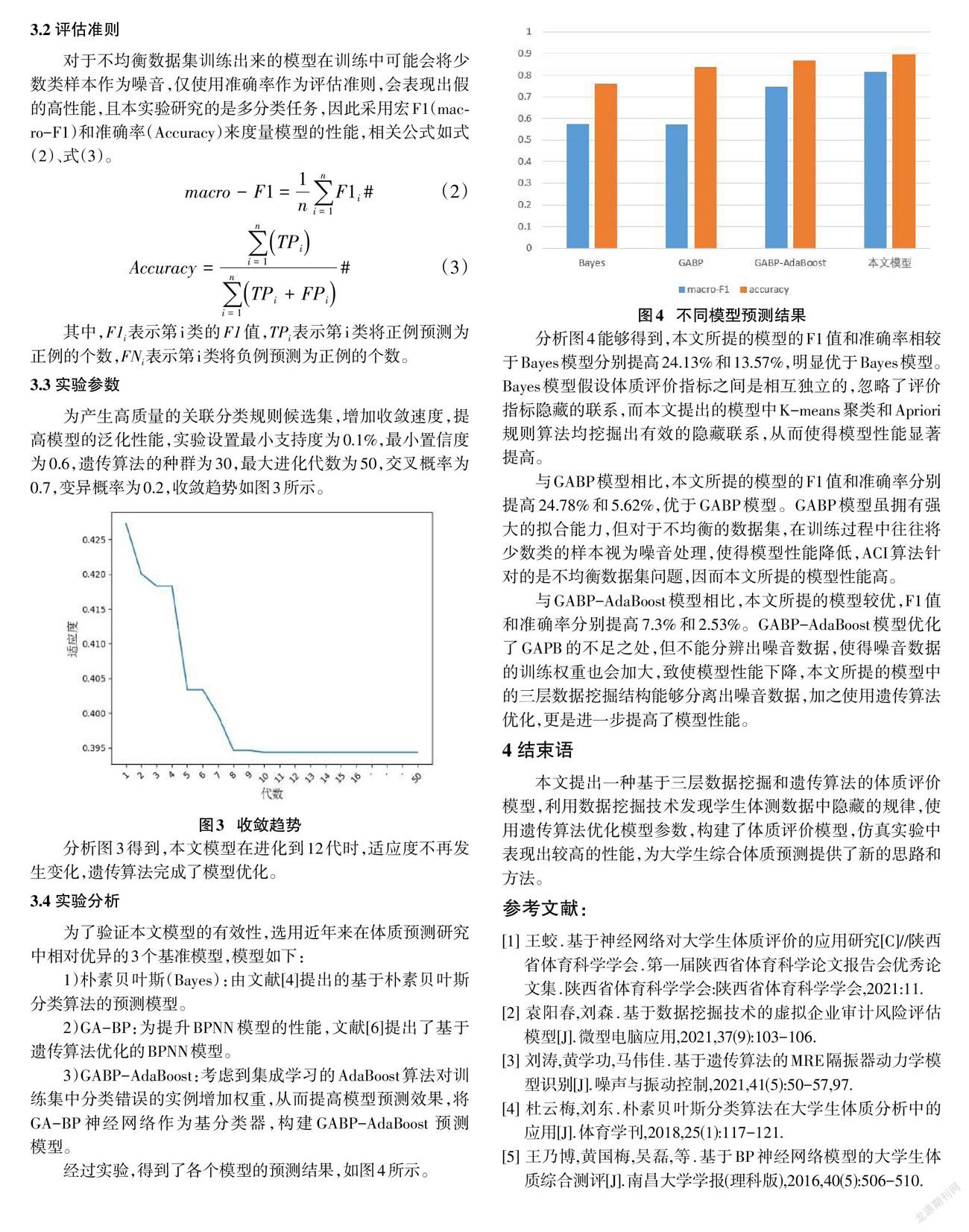
经过实验，得到了各个模型的预测结果，如图4所示。

分析图4能够得到，本文所提的模型的F1值和准确率相较于Bayes模型分别提高24.13%和13.57%，明显优于Bayes模型。Bayes模型假设体质评价指标之间是相互独立的，忽略了评价指标隐藏的联系，而本文提出的模型中K-means聚类和Apriori规则算法均挖掘出有效的隐藏联系，从而使得模型性能显著提高。

与GABP模型相比，本文所提的模型的F1值和准确率分别提高24.78%和5.62%，优于GABP模型。GABP模型虽拥有强大的拟合能力，但对于不均衡的数据集，在训练过程中往往将少数类的样本视为噪音处理，使得模型性能降低，ACI算法针对的是不均衡数据集问题，因而本文所提的模型性能高。

与GABP-AdaBoost模型相比，本文所提的模型较优，F1值和准确率分别提高7.3%和2.53%。GABP-AdaBoost模型优化了GAPB的不足之处，但不能分辨出噪音数据，使得噪音数据的训练权重也会加大，致使模型性能下降，本文所提的模型中的三层数据挖掘结构能够分离出噪音数据，加之使用遗传算法优化，更是进一步提高了模型性能。

4 结束语

本文提出一种基于三层数据挖掘和遗传算法的体质评价模型，利用数据挖掘技术发现学生体测数据中隐藏的规律，使用遗传算法优化模型参数，构建了体质评价模型，仿真实验中表现出较高的性能，为大学生综合体质预测提供了新的思路和方法。

参考文献：

[1] 王蛟.基于神经网络对大学生体质评价的应用研究[C]//陕西省体育科学学会.第一届陕西省体育科学论文报告会优秀论文集.陕西省体育科学学会：陕西省体育科学学会，2021：11.

[2] 袁阳春，刘森.基于数据挖掘技术的虚拟企业审计风险评估模型[J].微型电脑应用，2021，37（9）：103-106.

[3] 刘涛，黄学功，马伟佳.基于遗传算法的MRE隔振器动力学模型识别[J].噪声与振动控制，2021，41（5）：50-57，97.

[4] 杜云梅，刘东.朴素贝叶斯分类算法在大学生体质分析中的应用[J].体育学刊，2018，25（1）：117-121.

[5] 王乃博，黄国梅，吴磊，等.基于BP神经网络模型的大学生体质综合测评[J].南昌大学学报（理科版），2016，40（5）：506-510.

[6] 许珊珊，曹冶，崔洪珊.GA-BP神经网络预测大学生体质的模型构建研究[J].重庆理工大学学报（自然科学），2018，32（7）：162-168.

[7] Witten I H，Frank E，Hall M A.Embedded machine learning[M]//Data Mining：Practical Machine Learning Tools and Techniques.Amsterdam：Elsevier，2011：531-538.

[8] 教育部关于印发《国家学生体质健康标准（2014年修订）》的通知[EB/OL].[2021-07-20]. http：//www.moe.gov.cn/s78/A17/twys_left/moe_938/moe_792/s3273/201407/t20140708_171692.html.

[9] 王晓峰，王祥全.大学生人口身体素质变动及其问题成因分析[J].人口学刊，2018，40（2）：86-95.

[10] 崔巍，贾晓琳，樊帅帅，等.一种新的不均衡关联分类算法[J].计算机科学，2020，47（S1）：488-493.

【通联编辑：谢媛媛】

收稿日期：2021-11-08

作者简介：陈兴（1994—），男，河南焦作人，硕士，研究方向为计算机软件开发与应用;马致明（1964—），男，教授，硕士，研究方向计算机辅助教育、软件开发与应用。