基于全卷积网络和自编码的高光谱图像分类

董朋欣，董安国，李楚婷，梁苗苗

1.长安大学 理学院，西安 710064

2.江西理工大学 信息工程学院，江西 赣州 341000

关于高光谱图像（hyperspectral image，HSI）分类方法的研究，一直以来都是遥感影像信息系统的热点课题，在农业、航天、环境、气象等领域[1]引起了极大关注。高光谱图像具有高覆盖率和空谱域信息合一的特性。随着“高分五号”对地观测卫星[2]的发射成功，所得到的光谱数据维数越来越高，极大引发了“维度灾难”，与此同时，HSI还存在标签数据较少的问题。

在分类方法中，传统的支持向量机[3]（SVM）、稀疏自编码[4]（SAE）等方法仅利用了图像的光谱信息，导致出现图像分类精度低、分类结果杂乱等问题。而多尺度自适应稀疏表示[5]（MASR）考虑到不同尺度之间存在既互补又相关的分类信息，提出自适应稀疏融合矩阵；基于复合核的支持向量机算法[6]（CK-SVM），同时利用了谱特征和空间特征，优于传统的SVM方法。近年来，深度学习凭借自身非线性表征能力强、移植性高的优点，在图像分类方面取得极大进步。Feng等人采用堆栈自动编码器[7]和深度置信网络[8]对高光谱数据进行无监督分类学习；Chen等人[9]通过改进卷积神经网络（CNN），将邻域块作为网络输入，提出三维CNN（3D-CNN）网络框架；文献[10]提出一种通过上下文编码、多径解码和边界划分提高性能的语义分割模型；王立伟等人[11]将深度迁移学习用于HSI分类；Mahajan等人[12]利用预训练好的残差网络提取图像特征，并用SVM进行分类（Resnet-SVM）；基于CNN的全卷积网络[13]，将不同跳级结构有效融入深层特征和浅层特征。由于HSI地物的复杂性，空间、纹理等特征仍没有得到很好的提取，且有限的标记样本极大限制了对深度网络模型的训练。

针对此问题，本文提出一种基于全卷积网络和堆栈稀疏自编码（sparse stacked auto-encoder，SSAE）的分类算法。通过迁移预训练好的全卷积网络参数，提取数据多尺度几何结构特征，然后选取其特征的像素邻域信息，并与具有光谱特征的原高光谱数据进行拼接融合，最后将此特征的像元输入SSAE网络得到最终的多尺度空谱融合特征，并连接Softmax分类器完成所提空谱特征的分类。

1 全卷积网络和堆栈稀疏自编码器

1.1 全卷积网络

对于像素级分割的全卷积网络[13]（fully convolutional network，FCN）而言，它可以预测图中每一个像素的分类结果，是一个像素级端对端的学习结构，它将全连接层转化为卷积层，获得与原数据空间维度一致的特征，保留了其图像的空间结构，并且输入图像的尺寸更加灵活、方便。研究证实，大规模自然图像数据下训练得到的深度学习网络都有较强的泛化能力[14]。因此，FCN实现过程用VGG-16[15]网络做初始化，在此基础上进行微调。图1为FCN的简易结构图，图中矩形表示卷积层，网格表示池化层，其中卷积层的核尺度标记在矩形内部（如3×3conv，64表示64个大小为3×3的卷积核），池化层步长为2，图中也直观的展示了FCN在PaviaU数据集（3.1节介绍）下各网络结构层所提取的特征效果。具体操作步骤如下：

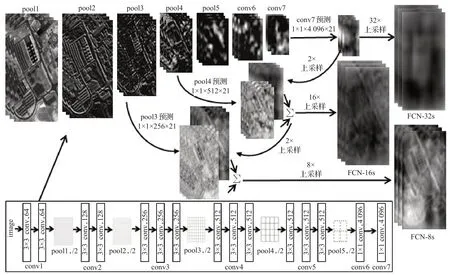
图1 FCN结构示意图（以PaviaU数据为例）Fig.1 FCN structure diagram（takeing PaviaU data as an example）

（1）首先保留VGG-16网络中所有卷积层和池化层，再将VGG-16中的全连接层（fc6、fc7）转化为卷积层（conv6、conv7），图中也显示了FCN部分网络结构（池化层和conv6、conv7）所提取的特征效果。

（2）在conv7层后，连接conv7预测层，并且对其预测层执行32倍上采样操作，即FCN-32s，所得到的空间结构特征与输入图像大小一致。

（3）加入2种跳级结构：第一种，在pool4层后，连接pool4预测层，然后对conv7预测层进行步长为2的上采样，并与pool4预测层相加融合，再将融合特征执行16倍上采样操作，实现像素级图像分割，即FCN-16s。第二种，在pool3层后，连接pool3预测层，再将FCN-16s操作步骤中的融合特征进行步长为2的上采样，并与pool3预测层逐数据相加融合，最后将所得的融合特征执行8倍上采样操作，即FCN-8s。

从图中可以看出，FCN-8s有效结合了浅层信息和深层信息，所捕获到的多尺度几何结构特征更为精细。

1.2 堆栈稀疏自编码器

堆栈稀疏自编码器[4]（SSAE）是借助稀疏自编码[4]（包含编码和解码两部分）实现相邻层级之间的参数学习，如图2为四隐层的堆栈稀疏自编码网络模型，包含六层层级结构的前馈型拓扑无环神经网络，它将前一层自编码器的编码部分作为后一层自编码器的输入，通过逐层无监督学习策略逐步堆栈形成，可提取出图像的深层结构特征。如果将其最后一个隐层与分类器连接，则可通过有监督微调实现分类。

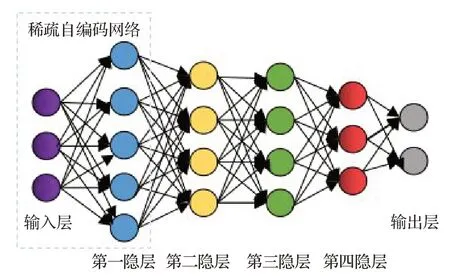
图2 堆栈稀疏自编码网络模型Fig.2 Sparse stacked auto-encoder network model

本文以最小平方误差作为网络训练的损失度量准则，SSAE的目标优化函数[4]用下式进行表示：

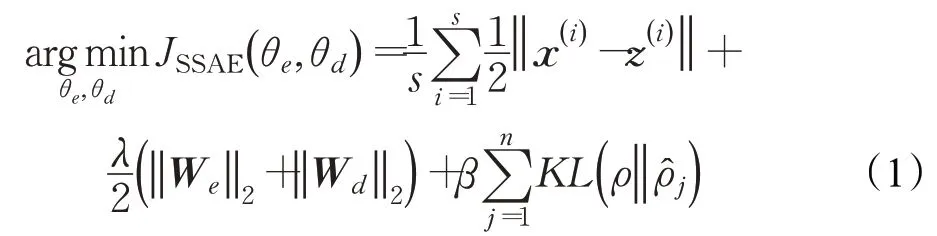
式中，s为输入样本总数量，x(i)为第i组样本原输入值，z(i)为第i组样本重构输出值，λ为权重衰减系数，ρ为期望激活比例，β为稀疏性正则项系数。

假设网络有四个隐层，输入层节点数为lin，输出层节点数为lout，每个隐层的节点数分别为l1、l2、l3、l4，则SSAE网络可表示为：lin-l1-l2-l3-l4-lout。其中输入层节点数为输入数据的特征维度，输出层节点数为分类对象类别数，一旦实验数据集确定，输入层和输出层节点数也随之确定。而隐藏层节点数可自行设置，但不合理的节点数选取会造成数据欠拟合或过拟合，因此选取合适的隐藏层节点数显得尤为重要。文献[16]提出的经验公式可快速有效地确定隐层节点数，公式如下：

其中，lh为隐层节点数，lh-为前一层节点数，lh+为后一层节点数。

但当输入数据的特征维度过高时，发现此方法求得的节点数较多，导致网络运行时间稍长，因此，在此基础上本文提出新的经验公式：

式中输出层节点数为lout。

2 基于全卷积网络和堆栈稀疏自编码的分类算法

由于HSI标记样本有限，不能较好地对深度网络参数进行训练。研究表明，大规模自然图像数据下训练得到的网络，其滤波器参数具有较好的迁移能力[14]。本文将利用预训练好的FCN-8s网络，挖掘图像多尺度几何结构特征，由于FCN-8s参数是在三维图像数据集（RGB图像）上学习的，所以先对HSI降维处理。对此，提出一种基于全卷积网络和堆栈稀疏自编码的分类算法（FCN8s-SSAE），由提取多尺度特征和融合空谱特征两部分组成，如图3所示，具体步骤如下：

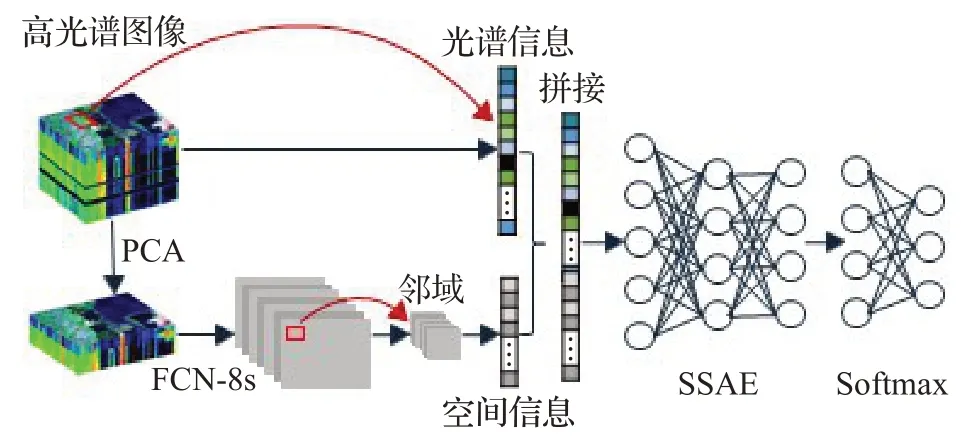
图3 FCN8s-SSAE算法模型图Fig.3 FCN8s-SSAE algorithm model diagram

（1）以自然图像集上训练的VGG-16网络为初始化，在此基础上进行微调（如1.1节所述），形成FCN-8s网络，并通过PASCAL VOC 2011数据集（其包含1个背景类别和20个目标类别），训练FCN-8s网络参数[13]。

（2）迁移已训练好的FCN-8s参数，将HSI通过PCA[17]进行降维，并取其前三个主成分作为FCN-8s的输入，提取HSI多尺度几何结构特征，即21个空间结构图。

（3）以空间结构图中每个像素点为中心，选取其给定窗口k×k大小的像素邻域块，将邻域块数据按列拉直成一维向量，获取数据空间信息。

（4）把所获取的空间信息与具有光谱信息的原高光谱数据进行拼接，形成初始融合特征。

（5）最后将初始融合特征的像元输入SSAE网络得到最终的多尺度空谱融合特征，并连接Softmax分类器[18]完成所提特征的分类。

3 实验与分析

3.1 实验数据和评估方法介绍

本文选取三组公开的遥感图像数据集进行分类实验，并通过整体精度OA、平均精度AA、Kappa系数三个评估指标进行定量分析。数据集介绍如下：

IndianP数据：Indian Pines影像由波长为0.4～2.5μm，大小为145×145的像素点组成，包含200个光谱波段（移去受水汽等干扰因素的20个波段）和10 249个样本点，共16类地物（如草地、农田等）。图4（a）显示了该数据集的伪彩图（波段50，27，17）和真实地物图。

PaviaU数据：Pavia University影像由空间分辨率为1.3 m，大小为610×340的像素点组成，包含103个光谱波段（移去受噪声等干扰的12个波段）和42 776个样本点，共9种地物（如树、沥青道路、牧场等）。图4（b）为该数据集的伪彩图（波段26，47，100）和真实地物图。

图4 实验数据的伪彩图和真实地物图Fig.4 Pseudo color map and real object map of experimental data

SalinasF数据：Salinas影像大小为512×217×204，空间分辨率为3.7 m，共16种地物（如葡萄园、蔬菜等），包含54 129个样本点。图4（c）显示了该数据集的伪彩图（波段77，48，18）和真实地物图。

3.2 参数分析与设置

本文所提算法FCN8s-SSAE中，所含超参数主要有邻域窗口大小k，自编码网络中的权重衰减系数λ、稀疏性正则项系数β、期望激活比例ρ以及隐层节点数lh、隐层层数。

邻域窗口大小k选取范围在3到11之间。图5（a）显示，邻域窗口尺寸与整体分类精度呈现两侧低、中间高的走势。当窗口较小或较大时，由于空间特征利用不足或者邻域信息中易引入异类像元的问题，导致整体分类精度较低。因此，依次设定三组数据集的邻域窗口参数k分别为7、5、7。

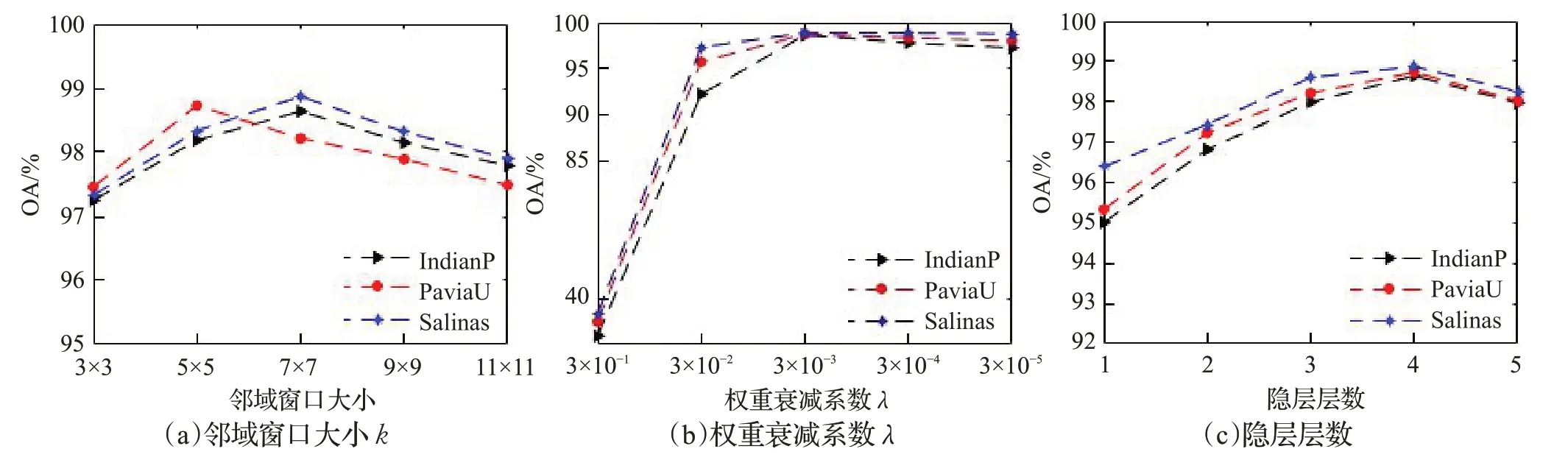
图5 参数k、λ、隐层层数对实验数据整体精度的影响Fig.5 Effect of parameter k、λand number of hidden layers on overall accuracy of experimental data

权重衰减系数λ在3×10-1至3×10-5范围之间进行选取，如图5（b）所示，三组实验数据在10-1时所得到的分类精度很低，在10-2时精度快速提高，随后在10-3到10-5之间趋于稳定。因此，参数λ在三组实验数据集上均设为3×10-3最为合适。

稀疏性正则项系数β和期望激活比例ρ均属于稀疏性约束参数，于是对这两个参数同时进行实验分析，其中β、ρ选取范围分别在1至5和0.2至0.9之间。图6显示，参数β在2到4范围，ρ在0.3到0.6范围取值时，实验结果较为稳定且分类精度都较好。所以，三个数据均设置ρ=0.3，IndianP和Salinas数据设置参数β=2，PaviaU数据设置β=3。

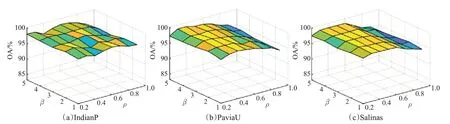
图6 稀疏约束参数β和ρ对实验数据整体精度的影响Fig.6 Effect of sparsity constraint parameterβandρon overall accuracy of experimental data

隐层层数选取范围在1到5之间。由图5（c）可知，随着网络层数的增加，分类精度不断提高，出现这样的现象是因为多隐层网络比单隐层网络能更好对数据进行表征，学习到更为抽象的数据特征。但这种提高是有上限的，当隐层层数过多时，会出现梯度消失问题，导致准确率降低，因此隐层层数的设置合适就好。实验得出，三组数据集的隐层层数均设置为4最好。

隐层节点数lh可根据改进的公式（3）求解方程组得到，解得三组数据集各网络层节点数分别为1 229-140-47-27-21-16、628-75-26-15-12-9、1 233-140-47-27-21-16。为了验证公式（3）改进有效，于是与文献提出的公式（2）进行对比，通过公式（2）求解得到的各层节点数分别为1 229-510-212-88-37-16、628-264-111-47-20-9、1 233-515-215-90-38-16。表1展示了两种经验公式所得节点数对分类精度的影响，结果显示改进后的公式（3）分类准确率更好，且较少的节点数使网络运行时间缩短。

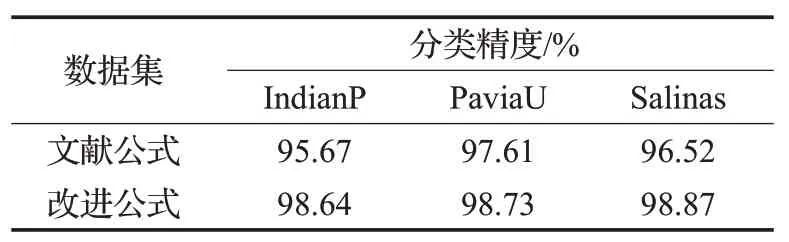
表1 隐层节点数经验公式对比Table 1 Comparison of empirical formulas of hidden layer node number

3.3 FCN8s-SSAE算法的分布评估

本文所提算法FCN8s-SSAE主要由全卷积网络的多尺度几何特征提取和自编码器的空谱特征融合两部分完成。为了对算法各步骤的有效性进行证明，首先，将仅利用原光谱信息的光谱特征，仅利用全卷积网络和邻域块进行特征提取出的空间特征，以及本文算法所提取出的空谱特征做进一步分析。在PaviaU和Salinas数据集上，利用t-SNE[19]方法对光谱、空间、空谱各特征进行可视化分析。从图7观察到，光谱特征未能完全将不同种类样本分开，而空间特征很好地将不同种类间的样本进行划分，但同类样本却出现不同程度的离散化，相比本文所提出的空谱特征，样本点呈现类间可分、类内聚集的状态，更加验证了空谱融合步骤的有效性，从而也说明本文所提特征可分。

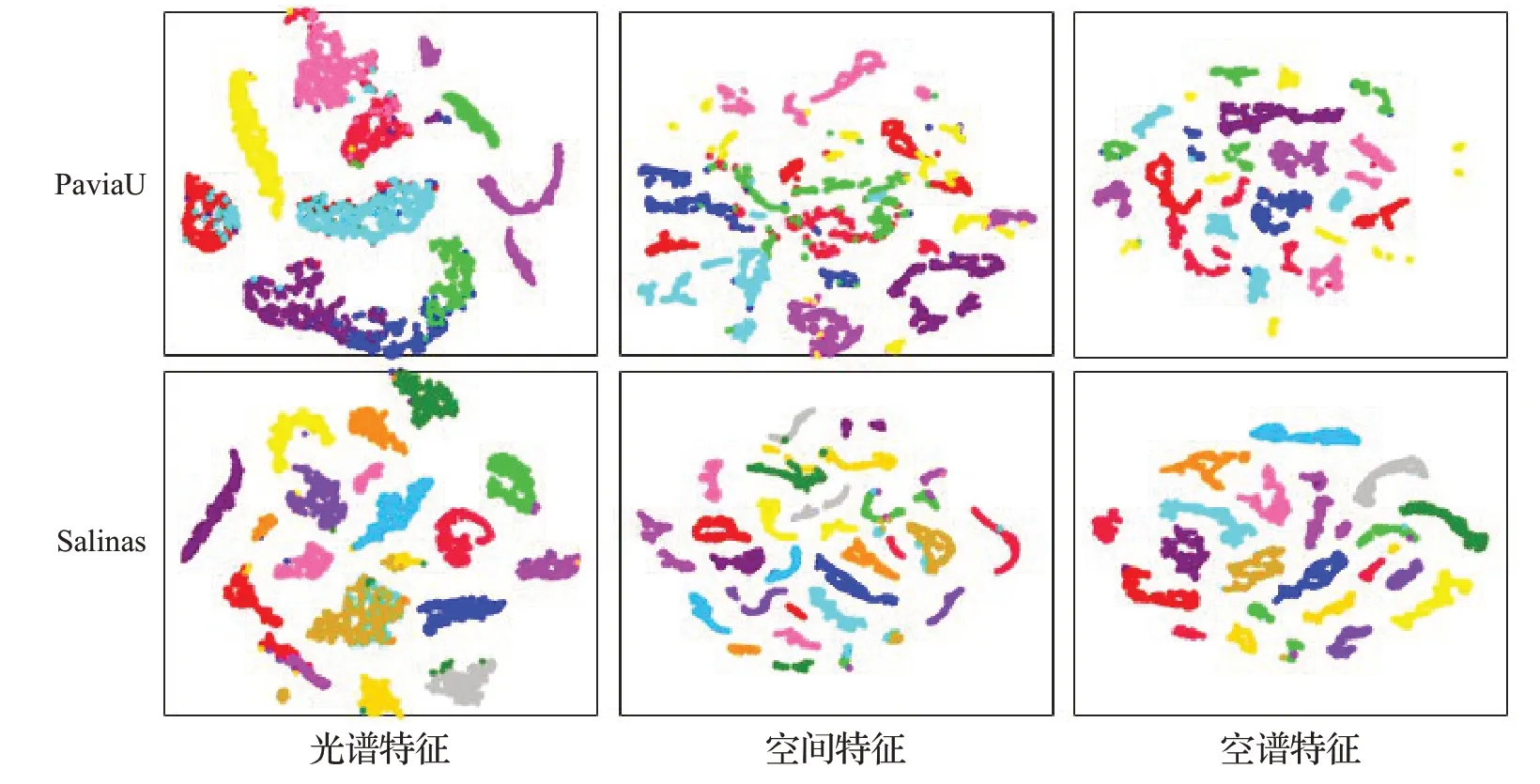
图7 基于t-SNE方法的各特征可视化分布Fig.7 Visual distribution of features based on t-SNE method

3.4 实验结果分析

为了对本文算法进行有效验证，现将SAE、CK-SVM、MASR、3D-CNN、Resnet-SVM方法，FCN-32s、FCN-16s分别与SSAE结合形成的FCN32s-SSAE、FCN16s-SSAE算法，以及本文算法FCN8s-SSAE（共8种算法）进行对比分析。对于Indian数据，由于该数据各目标类分布不均匀（如Oats类有20个样本，Soybean-mintill类有2 345个样本，见表2），因此实验随机选取每类标记样本的10%作为训练样本，其余样本用作测试。对于PaviaU数据和Salinas数据，分别选取各自每类样本200个和60个作为训练样本。其中，表2～4列出了6种算法在各数据集下的分类精度，图8～10分别展示了6种算法的分类结果图。

图8 IndianP地区各方法的分类结果Fig.8 Classification results of various methods in IndianP

实验观察到，仅利用光谱信息的SAE方法整体分类精度较低、分错点较多，均得到较差的分类结果；仅利用空间信息的Resnet-SVM算法分类结果有所提高，但在不同数据集上实验，发现分类结果不够稳定且精度提升有限；CK-SVM、MASR、3D-CNN和FCN32s-SSAE、FCN16s-SSAE以及本文算法均通过融合空谱特征极大提高了分类精度，边界区分效果明显改善。表2～4显示，在所有实验数据上，本文算法的各目标类分类精度均达到90%以上，小样本类也取得很好的分类准确率（如表2中的小样本Oats类，只有20个样本），但CKSVM、MASR方法在IndianP数据分类中整体精度很高，却牺牲了小样本类的准确性。在所有实验数据上发现，FCN16s-SSAE算法精度优于FCN32s-SSAE，FCN8s-SSAE算法精度优于FCN16s-SSAE，三组数据集上均得到FCN8s-SSAE算法的分类精度最好，这是因为FCN-8s网络通过跳级结构对图像的浅层特征和深层特征进行多次结合，所获得的结构特征更为精细，同时图1也直观地展示了这一结论。3D-CNN在三组数据集上也得到较好的分类精度，不足的是程序运行时间过长（以小时单位计算）。综上分析，本文所提的FCN8s-SSAE算法优于其他算法，所提取的最终融合特征具有较强的可分性，极大改善了HSI的分类结果。

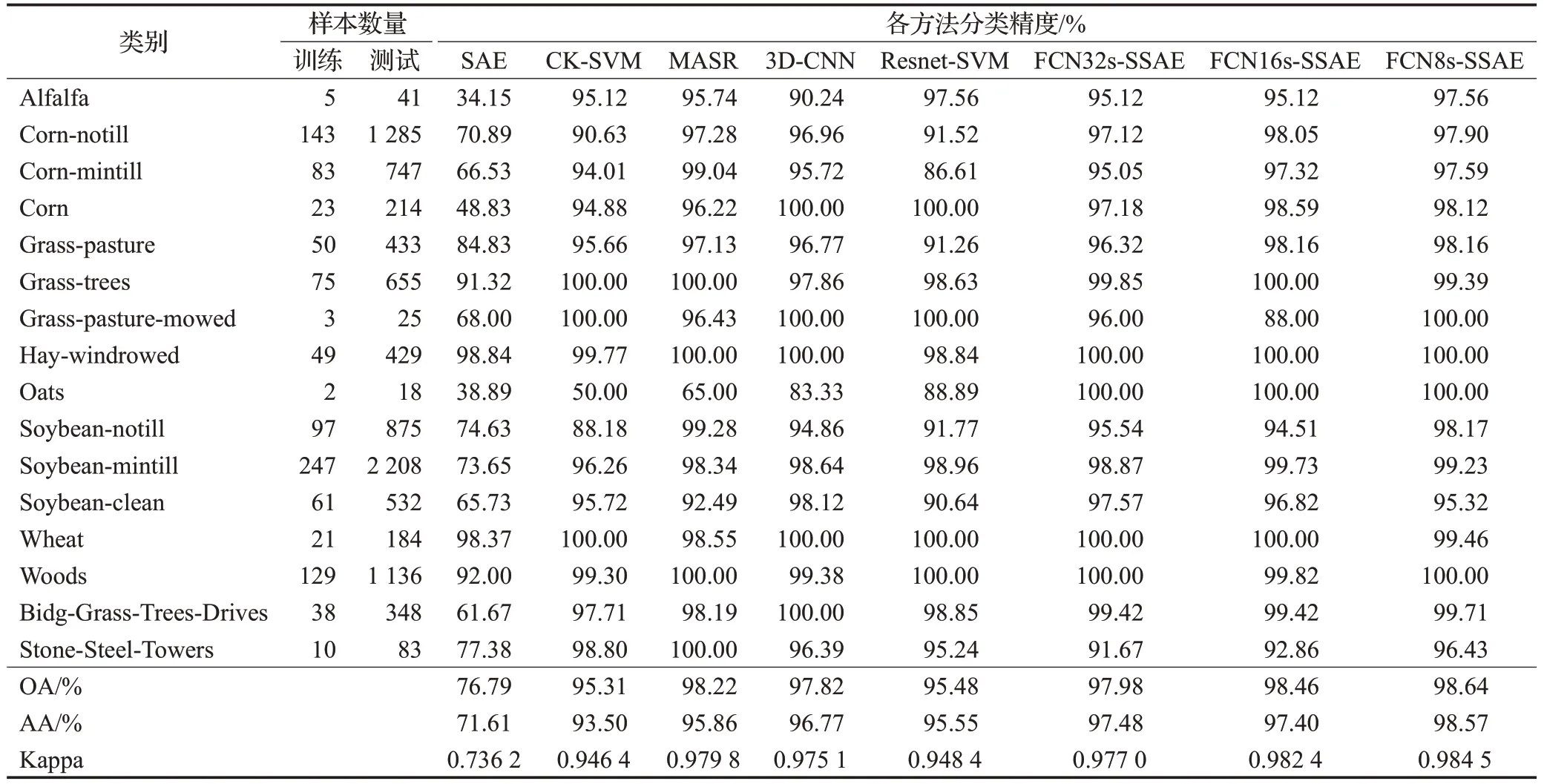
表2 IndianP地区各方法的分类精度Table 2 Classification accuracy of various methods in IndianP

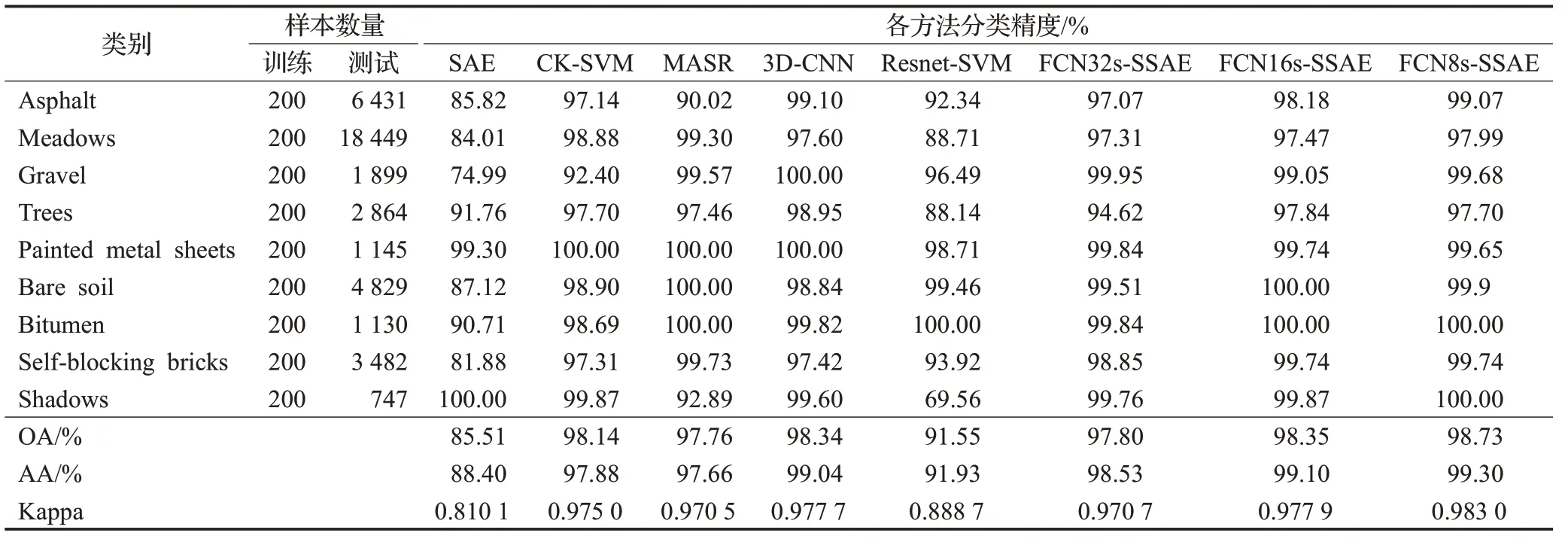
表3 PaviaU地区各方法的分类精度Table 3 Classification accuracy of various methods in PaviaU

表4 Salinas地区各方法的分类精度Table 4 Classification accuracy of various methods in Salinas

为了验证FCN8s-SSAE策略的有效性，图11通过改变训练样本数量对各类方法进行测试。结果显示，训练样本数量与分类样本整体呈现逐步升高的曲线走势，空谱融合算法优于仅考虑光谱特征的方法，以本文算法（FCN8s-SSAE）作为网络输入的特征提取方法均优于其他算法。

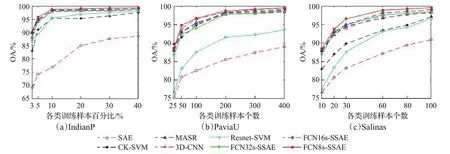
图11 训练样本数量对各类算法精度的影响Fig.11 Influence of number of training samples on accuracy of various algorithms

图9 PaviaU地区各方法的分类结果Fig.9 Classification results of various methods in PaviaU

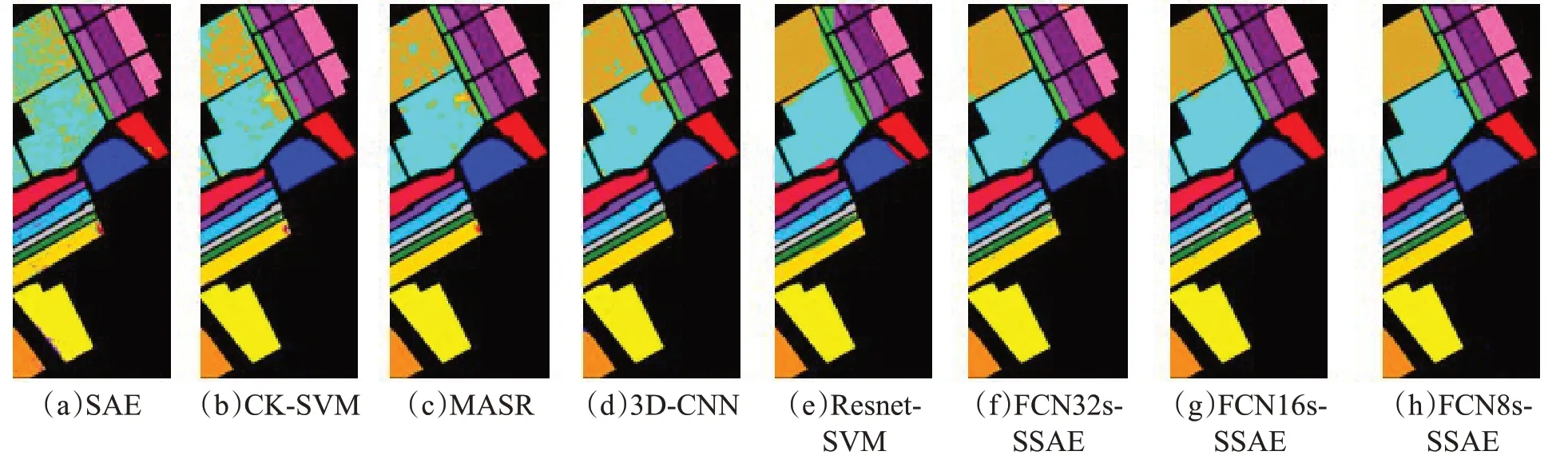
图10 Salinas地区各方法分类结果Fig.10 Classification results of various methods in Salinas

4 结束语

根据高光谱图像空谱信息合一、数据高度非线性的特点，提出一种基于全卷积网络和堆栈稀疏自编码的分类算法。迁移预训练好的FCN-8s滤波器参数对图像多尺度几何结构特征进行提取，改善了神经网络的学习与优化。为了挖掘更具可分性的多尺度空谱特征，将其邻域特征与谱特征进行拼接作为堆栈稀疏自编码网络的输入，并通过Softmax分类器验证最终所获得特征的有效性和判别性。与现有的几种方法相比，本文算法（FCN8s-SSAE）得到了较为满意的分类精度，且边界区域分类效果得到改善。本文仍然存在有待改进的地方，如超参数设置依靠大量实验分析和人为经验设定，应考虑更为高效合理的超参数设置方法，并且同时利用并行计算提高算法运行效率。